网格质量

Simcenter STAR-CCM+ 提供了多个网格单元度量，可用来确定体网格的整体质量。通常，质量较差的体网格不一定会引发求解器运行时问题，但确实会降低求解精度和效率。

评估网格整体质量时，需考虑以下几个因素：

网格密度 - 在高梯度区域中，网格是否足够密集，是否能够精确捕捉流体特征？
网格分布 - 高梯度区域和低梯度区域之间的网格分布是否最佳？
近壁层 - 网格是否包含近壁层来计算湍流和热传递效应？

在局部（网格单元到网格单元）级别中，需考虑以下因素：

长宽比 - 预期流态的长宽比是否合理？
y+ 范围 - 选定湍流模型的 y+ 值是否合理？
体积比 - 网格单元体积与其邻近的网格单元体积的比值是否合理？
偏斜角 - 网格单元偏斜角是否已达到极限？

对于流体流计算，网格质量对扩散通量和对流通量的计算影响最大：

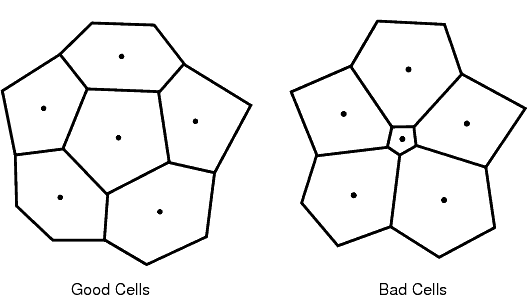
要获得最佳精度和稳定性的对流通量，连接相邻网格单元形心的线最好尽可能靠近分隔网格单元的面的形心。此问题的二维示例如下所示：

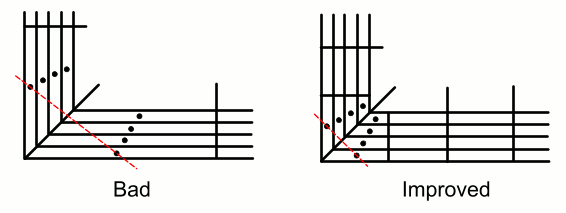
在此示例中，通过加密网格而在角附近创建长宽比较低的网格单元，可以提高网格质量。
要获得最佳精度和稳定性的扩散通量，连接相邻网格单元形心的线最好尽可能与分隔网格单元的面接近正交。在 Simcenter STAR-CCM+ 中，此角度为网格单元偏斜角。下面显示了高偏斜角的二维示例：

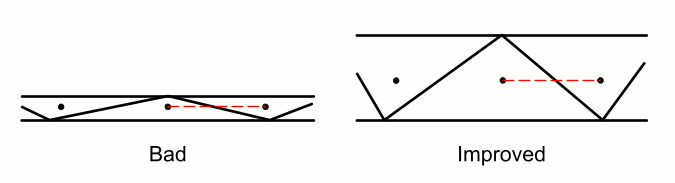
在此示例中，通过加密网格而创建长宽比较低的网格单元，可以提高网格质量。

网格度量

网格单元质量有多个度量，其中有些仅适用于特定的网格单元形状。目前 Simcenter STAR-CCM+ 中可用的度量包括：

面有效性
网格单元质量
体积变化
网格单元偏斜角
Chevron 质量指示器
最小二乘质量
网格单元翘曲质量

为了创建并可视化面有效性和体积变化度量，首先应在激活相应物理模型的情况下初始化求解。在上述情况下，仅需在执行初始化之前选择三维空间模型。

上述每个度量均可使用阈值加以标识，并可视化为几何或标量场景的一部分。请参见标识和可视化坏网格单元。

面有效性

面有效性是面法向相对于其关联网格单元形心的正确性的面积加权度量。

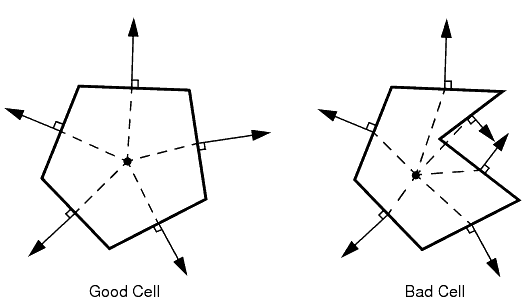
在高质量的网格单元中，面法向指向外部，远离网格单元形心。在面有效性较差的网格单元中，一个或多个面法向指向内部，朝向网格单元形心。当面有效性为 1.0 时，意味着所有面法向均正确指向远离网格单元形心的方向。当值低于 1.0 时，意味着某些网格单元面法向指向内部，朝向网格单元形心，这指示存在某种形式的凹陷。当值低于 0.5 时，表示负体积网格单元。面有效性低于 1.0 的网格单元被视为坏网格单元。

要移除无效网格单元，可以在该对话框中输入面有效性度量所需的最小值。

网格单元质量

网格单元质量度量算法以网格单元梯度计算方法的混合高斯与最小二乘法为基础。它不仅是网格单元形心相对于面相邻网格单元的几何分布函数，也是网格单元面的方位函数。通常，其面非正交程度较高的平网格单元的网格单元质量往往较差。

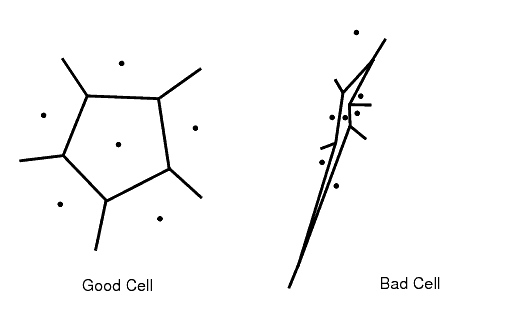
质量为 1.0 的网格单元被视为完美网格单元。例如，立方网格单元便是这样一种完美的网格单元。但其他多面体网格单元形状也可以具有接近合一值的网格单元质量。衰减网格单元的质量接近零。面网格质量低于 1.0e-5 的网格单元被视为坏网格单元。

根据为分析选择的物理模型，网格单元的网格单元质量可能会相当低，且仍可提供有效的求解。但是，质量较差的网格单元可能会影响求解的稳定性和精度。只能为三维网格定义网格单元质量。

要移除无效网格单元，可以在该对话框中输入网格单元质量度量所需的最小值。

体积变化

体积变化度量描述网格单元体积与其最大的相邻网格单元体积之比。

该值为 1.0 时，指示该网格单元的体积大于或等于其相邻网格单元。当网格单元体积相对于其相邻网格单元（如薄元或平网格单元）体积减小时，可以使用体积变化度量标记此网格单元。两个网格单元之间的体积跃变过大时，可能会导致求解器不精确和不稳定。体积变化为 0.01 或更小的网格单元被视为坏网格单元。

要移除无效网格单元，可以在该对话框中输入体积变化度量所需的最小值。

网格单元偏斜角

此偏斜度量旨在反映面两侧的网格单元是否采取允许物理量扩散的方式形成，而又不会导致这些物理量变得无限大。

要了解此度量，考虑面和面任一侧的网格单元形心的以下二维图：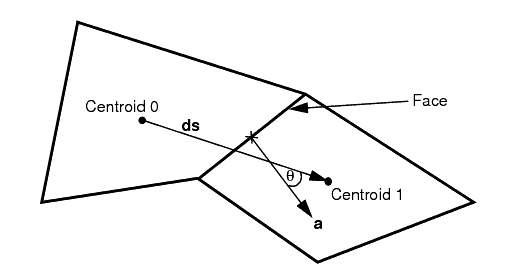

偏斜角 $θ$ 为面网格面积矢量 $a$ （面法向）与连接两个网格单元形心的矢量 $d s$ 之间的夹角。角度为零表示完美的正交网格。Simcenter STAR-CCM+ 内部面中存储的变量无法显示。而网格单元所有面的最差偏斜角将存储在该网格单元中。因此，两个网格单元通常具有相同的偏斜角，与其共享的面对应。

偏斜角大于 $85^{o}$ 的网格单元被视为坏网格单元。

当偏斜角大于或等于 $90^{o}$ （可能出现在凹网格单元中，其中两个网格单元的形心均位于边界面的同一侧）时，通常会导致出现求解器收敛问题。之所以会出现问题，是因为已传输标量变量的扩散项在分母中包含点积 $a \cdot d s$ ，而当 $a$ 和 $d s$ 之间的角度为 $90^{o}$ 时，此点积为零。尽管 Simcenter STAR-CCM+ 会注意避免出现这种除以零的错误，但在这种情况下，扩散计算的精度和稳定性均会降低。

Chevron 质量指示器

Chevron 网格单元是在公共面以一定角度相交的细薄网格单元对，该角度使得连接网格单元中心的线不会穿过公共面。

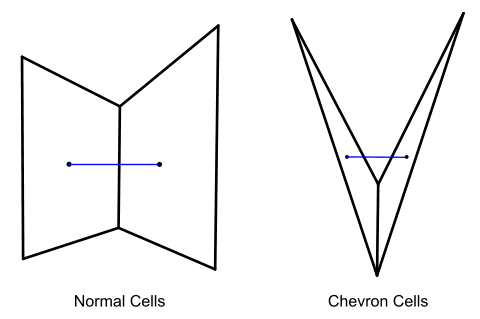
Chevron 质量范数 $c$ 可用于确定网格单元能否被分类为 Chevron 网格单元：

c = 1 - \frac{d p \cdot d p}{m a x (d p \cdot d v)}

其中：

$d p$ 为从面中心投影到连接网格单元中心的线的矢量。
$d v$ 为从面顶点到面中心的矢量
计算 Chevron 质量范数时，max 函数将遍取所有面节点。

可使用矢量 $d p$ 来计算 Chevron 质量范数：

d p = (\frac{A_{f} \cdot d x}{A_{f} \cdot d s}) d s - d x

其中：

$A_{f}$ 为面网格面积矢量。
$d x$ 为从面中心到网格单元中心的矢量。
$d s$ 为连接两个网格单元中心的矢量。

Chevron 网格单元标记为 1.0，其他每个网格单元则标记为 0。Chevron 网格单元被视为坏网格单元。

最小二乘质量

此场函数是网格单元质量的指示器，它使用网格单元形心相对于其面相邻网格单元的网格单元形心位置的物理位置。

该场函数值以对称矩阵的最大特征值比率和最小特征值比率之比为基础：

\bar{\bar{M}} = \sum_{cell faces i}^{n} \frac{d s_{i} \otimes d s_{i}}{{| d s_{i} |}^{2}}

其中：

${d s}_{i}$ 表示从网格单元到相邻形心的矢量。

然后，场函数使用雅可比变换来计算特征值比率。完美网格单元的最小二乘质量为 1。此外，系统还提供了一个选项，将网格单元的边界面包括在边界网格单元计算中。

最小二乘质量低于 1.0e-3 的网格被视为坏网格单元。

网格单元翘曲质量

网格单元翘曲质量将标识翘曲的薄网格单元。这些类型的网格单元会导致流动求解器问题，特别是对于 LES/DES 和声学等需要最大程度减少耗散的高保真度模拟更是如此。

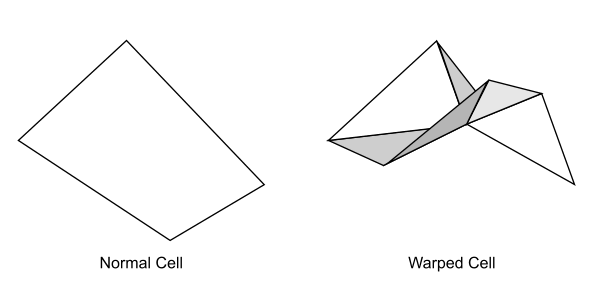
翘曲质量以测量面的网格单元翘曲角度为基础。网格单元翘曲角度定义如下：

2 * \arctan (\frac{d}{L})

其中：

d 为投影在面法向上的对等距离，定义如下： $d = \max [| (x_{i} - x_{i + 1}) \cdot n |]$ 。最大值将遍取该面的连续节点 $i$ ，且 $n$ 为该面的法向单位矢量。
L 为该面的特征长度尺度，定义如下： $L = \sqrt{A r e a}$ 。面积是面的面积值。

网格单元翘曲角度将以非线性方式比例缩放并转换为网格单元翘曲质量。网格单元翘曲质量范围为 0.0（表示翘曲质量最差）至 1.0（表示没有翘曲）。

网格单元翘曲质量低于 0.15（对应于网格单元翘曲角度 $50^{o}$ ）的网格单元被视为坏网格单元。通常，网格单元翘曲角度越小，其质量越佳。

只有长宽比小于 0.2 的网格单元，其翘曲质量值才能小于 1.0。

网格单元质量校正模型或坏网格单元检测模型中未包括网格单元翘曲质量。可以通过 Java 宏手动将网格单元翘曲质量添加到这些标准中，其中，最小值为 0.15，最大值为 1.0。