Equation of State Models Reference

The Equation of State models compute the density with respect to temperature and pressure.

Simcenter STAR-CCM+ provides the following models:

Constant Density (for gases, liquids, and solids)—based on the assumption that density is invariant throughout the continuum.
Ideal Gas (for gases)—uses the ideal gas law to express density as a function of temperature and pressure.
IAPWS-IF97 (Water) (for water)—for information on this model and the companion model for steam, see the IAPWS-IF97 models under Real Gas Models Reference.
Polynomial Density (for gases, liquids, and solids)—works on the assumption that the density is a function of temperature only.
Real Gas (for gases)—represents a family of models for situations outside the scope of the ideal gas law. See Real Gas Models Reference
Thermal Non-Equilibrium Ideal Gas (for gases)—for use at high temperatures and low densities, where the vibrational/electronic energy modes become active yet the density is low enough that equilibration does not occur. See also Thermal Non-Equilibrium Model Reference.
User Defined EOS (for gases, liquids, and solids)—when the other Equation of State models do not adequately describe your working fluid, this model allows you to specify the density and density derivatives using some user-defined expressions or tables of property data. When you specify thermodynamic properties such as density and enthalpy using tabular input data, Simcenter STAR-CCM+ can evaluate the necessary derivative terms with respect to pressure and temperature by numerically differentiating the tabular data. This calculation eliminates the need to provide more columns of data for the derivative terms. To increase accuracy and robustness of the solver, this derivative data can also be specified explicitly using tabular input data. When explicit derivative values are available, it is best to provide this derivative data to Simcenter STAR-CCM+.


Model Names and Abbreviations	Constant Density		CD
	Ideal Gas		Ideal
	IAPWS-IF97 (Water)		IAPWS-w
	Polynomial Density		PolyD
	Real Gas		Real
	Thermal Non-Equilibrium Ideal Gas		TNEq
	User Defined EOS		UDEOS
Theory	Ideal Gas Formulation Polynomial Density Formulation Real Gas Formulation Thermal Non-Equilibrium Formulation
Provided by	Continua > [physics continuum] > Models > Equation of State
Example Node Path	Continua > Physics 1 > Models > Constant Density
Requires	Flow: Coupled Flow or Segregated Flow (TNEq specifically requires Coupled Flow) Ideal, Real, and TNEq require Material: Gas or Multi-Component Gas IAPWS-w requires Material: Liquid
Properties	See Equation of State Properties.
Activates	Physics Models	For CD, Optional Models: Boussinesq Model For Ideal, IAPWS-w, PolyD, Real, and TNEq, Energy: Coupled Energy For TNEq, Thermal Non-Equilibrium: Thermal Non-Equilibrium. See Thermal Non-Equilibrium Model Reference. For Real, Real Gas Equation of State box. See Real Gas Models Reference.
	Model Controls (child nodes)	Density Limits (Ideal, TNEq) See Model Controls.
	Materials	See Material Properties.
	Monitors	Vib. Energy (TNEq, UDEOS)
	Field Functions	See Field Functions.

Equation of State Properties

The following table shows which properties are available for which equation of state model:


	Ideal	TNEq	UDEOS
Compressible			✓
Density Limiting	✓	✓
Incompressible	✓	✓

See Real Gas Models for the properties of individual real gas models.

Compressible: When On, this property specifies that the material is compressible (dependent on working pressure $p$ ).
Density Limiting: When On, this property activates the Density Limits option that is used to prevent negative densities.
Incompressible: When On, this property specifies that the gas is incompressible (not dependent on working pressure $p$ ).

Material Properties

The following table shows which material properties become available for which equation of state model:


	CD	Ideal	IAPWS-w	PolyD	TNEq	UDEOS
Critical Pressure			✓
Critical Temperature			✓
Density	✓					✓
Density Mass-Fraction Derivative						✓ (if the Multi-Component Gas Model or the Multi-Component Liquid model is activated)
Density Pressure Derivative						✓ (if Compressible is On)
Density Temperature Derivative						✓ (if an Energy Model is activated)
Enthalpy						✓ (if an Energy Model is activated)
Enthalpy Pressure Derivative						✓ (if an Energy Model is activated and Enthalpy is set to Table, h(T,p))
Entropy						✓ (if Compressible is On and an Energy Model is activated)
Molecular Weight		✓	✓		✓	✓ (if Compressible is On)
Molecule Type					✓
Polynomial Density				✓
Saturation Pressure			✓
Saturation Temperature			✓
Specific Heat	✓ (if an Energy Model is activated)	✓	✓	✓		✓ (if an Energy Model is activated)
Speed of Sound			✓			✓ (if Compressible is On)
Vibrational-Electronic Specific Heat					✓

See Real Gas Models for the material properties of individual real gas models.

Critical Pressure

Displays the model constant

p_{c}

(read-only).

Critical Temperature

Displays the model constant

T_{c}

(read-only).

Density

Specifies the density of the fluid

ρ

Density Mass Fraction Derivative

Specifies the partial derivative of the user-defined density with respect to mass-fraction for each mixture component

d (ρ) / d (Y_{i})

Density Pressure Derivative

Specifies the partial derivative of the user-defined density with respect to pressure

d (ρ) / d (p)

As an example, you can choose to model a compressible fluid by specifying density using a field function that is defined as:

图 1. EQUATION_DISPLAY

ρ = ρ_{0} + \frac{p}{c^{2}}

(185)

where $ρ_{0}$ is a constant, $p$ is the pressure, and $c$ is the (constant) speed of sound. In this example, you would specify the following field function for Density Pressure Derivative:

图 2. EQUATION_DISPLAY

\frac{d (ρ)}{d (p)} = \frac{1}{c^{2}}

(186)

and you would specify the constant $c$ for the speed of sound.

Density Temperature Derivative

Specifies the partial derivative of the user-defined density with respect to temperature

d (ρ) / d (T)

Enthalpy

Specifies the enthalpy

h

of the fluid using one of the following methods:


Method	Corresponding Method Node
Specific Heat Calculates the enthalpy by integrating the specified Specific Heat property: If the specific heat is specified with the Polynomial in T method, enthalpy is calculated as the integral of specific heat over T in the interval between the specified Standard State Temperature and T, plus the heat of formation. If the Heat Of Formation material property is not specified, the heat of formation value defaults to zero. If the specific heat is specified as Constant, the Standard State Temperature material property is not available and the standard state temperature is assumed to be 0 K. The heat of formation is also assumed to be zero. The calculated enthalpy is the same as using a constant polynomial with the same value for the Specific Heat material property, and the Standard State Temperature set to zero.	Specific Heat This node provides no properties.
Table, h(T) Tabulates enthalpy as a function of temperature.	Table(T) See Using Table(T).
Table, h(T,p) Tabulates enthalpy as a function of temperature and pressure.	Table(T,p) See Using Table(T,p).

Enthalpy Pressure Derivative

Specifies the partial derivative of the user-defined enthalpy with respect to pressure

d (h) / d (p)

Entropy

Specifies the entropy

s

of the fluid using one of the following methods:


Method	Corresponding Method Node
Isentropic Treats the entropy as a constant value, independent of temperature and pressure. For more information, see Entropy.	Isentropic This node provides no properties.
Table (T) (Only available at the component level) Tabulates entropy as a function of temperature.	Table (T) Specifies the entropy that is used to calculate the backwards reaction rates, using an interpolation table in temperature. See Using Table (T)
Table, s(T,p) Tabulates entropy as a function of temperature and pressure. Table, s(T,p) is the method name at the material level.	Table (T,p) Specifies the table of entropy values. The table must cover the full range of temperatures and pressures that are encountered in the simulation. The range must cover the total pressure and total temperature values, which are higher than the corresponding static quantities. If the table does not cover the full range, the total quantities may not converge. For individual species, entropy is interpolated from this table and used to calculate the backwards reaction rates for Complex Chemistry. See Using Table (T,p)
Table (T,p) Tabulates entropy as a function of temperature and pressure. Table (T,p) is the method name at the component level.

Molecular Weight

Specifies the molecular weight

M

Molecule Type

Describes the molecular structure using the following values:

0: atom
1: linear molecule
2: non-linear molecule

Polynomial Density

Specifies the density

ρ

using a polynomial in temperature, see Using Polynomial in T.

Saturation Pressure

Specifies the saturation pressure.

Saturation Temperature

Specifies the temperature for the corresponding saturation pressure at which the liquid boils into its vapor phase.

Specific Heat

Specifies the fluid-specific heat capacity

C_{p}

using one of the following methods:


Method	Corresponding Method Node
Constant (CD, Ideal, PolyD, UDEOS)	Constant Specifies the specific heat using a scalar profile value.
Gas Kinetics (CD, Ideal, PolyD) Uses the Gas Kinetics Method for Specific Heat.	Gas Kinetics This node provides no properties. Selecting the Gas Kinetics method adds the following material properties: Electronic Partition Function Specifies the partition function for electronic energy using a Number of Modes with Characteristic Temperatures $θ_{i}$ and Mode Degeneracies $g_{i}$ . See $Q_{e l}$ in Eqn. (163). Molecule Type Describes the molecular structure using the following values: 0: atom 1: linear molecule 2: non-linear molecule Standard State Temperature Specifies the temperature at which the standard state of the fluid is defined. The Standard State Temperature is used to calculate enthalpy. The enthalpy value varies with Standard State Temperature, but in direct proportion, so differences in enthalpy remain the same for different values of Standard State. Vibrational Partition Function For polyatomic molecules, specifies the partition function for vibrational energy using a Number of Modes with Characteristic Temperatures $θ_{i}$ and Mode Degeneracies $g_{i}$ . See $Q_{v i b}$ in Eqn. (163).
Fully Excited (TNEq)	Fully Excited This node provides no properties.
Polynomial in T (CD, Ideal, PolyD, UDEOS)	Polynomial in T See Using Polynomial in T. Selecting the Polynomial in T method adds the following material property: Standard State Temperature As for Gas Kinetics.
Table, Cp(T) (CD, Ideal, PolyD, UDEOS) Tabulates specific heat as a function of temperature.	Table(T) See Using Table(T).

Speed of Sound

Specifies the rate of acoustic propagation in the medium using one of the following methods:


Method	Corresponding Method Node
Constant (UDEOS)	Constant Specifies the speed of sound using a scalar profile value.
Equilibrium (UDEOS) Uses the Equilibrium Method.	Equilibrium This node provides no properties.
Field Function (UDEOS)	Field Function Specifies the speed of sound using a scalar field function.
IAPWS-IF97 (IAPWS-w)	IAPWS-IF97 This node provides no properties.
Table(T,p) (UDEOS, if an Energy Model is activated) Tabulates the speed of sound as a function of temperature and pressure.	Table(T,p) See Using Table(T,p).

For a multi-component material, you can set the speed of sound for the material as a property of the mixture. For a Eulerian multiphase material, you can set the speed of sound for each phase of the material as a property of the phase. Eulerian multiphase materials use the speed of sound in the dissipation term in the K-Epsilon and Reynolds Stress turbulence models only.

注	Eulerian multiphase models do not have a full implementation of this property for high Mach number (M > 0.3).

The speed of sound is used for certain boundary conditions (pressure outlet, mass flow inlet, and free-stream) when the flow is compressible. It also appears in the compressibility modification (dilatation dissipation) for the K-Epsilon and Reynolds Stress turbulence models.

Vibrational-Electronic Specific Heat

Specifies the vibrational-electronic specific heat

C_{p, v e}

using one of the following methods:


Method	Corresponding Method Node
Constant	Constant Specifies the specific heat using a scalar profile value.
Gas Kinetics Uses the Gas Kinetics Method for Specific Heat.	Gas Kinetics This node provides no properties. Selecting the Gas Kinetics method adds the following material properties: Electronic Partition Function Specifies the partition function for electronic energy using a Number of Modes with Characteristic Temperatures $θ_{i}$ and Mode Degeneracies $g_{i}$ . See $Q_{e l}$ in Eqn. (163). Vibrational Partition Function For polyatomic molecules, specifies the partition function for vibrational energy using a Number of Modes with Characteristic Temperatures $θ_{i}$ and Mode Degeneracies $g_{i}$ . See $Q_{v i b}$ in Eqn. (163).

Model Controls

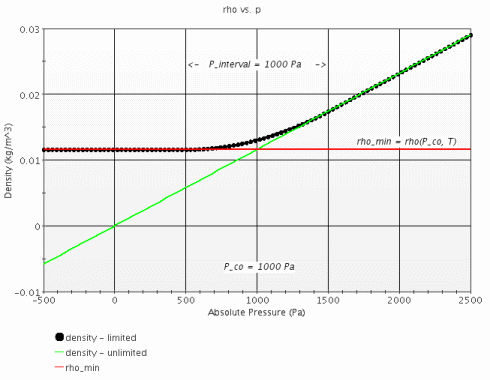
Density Limits

When the Density Limiting property is On, specifies the following density limits parameters that allow you to prevent negative densities:

Cut-off Pressure
Pressure Interval

The following figure shows a comparison of the limited and unlimited density as a function of absolute pressure. As seen from the figure, the limited density smoothly and continuously transitions from its unlimited value to a constant, minimum value, rho_min, over the course of the interval, P_interval, as specified by the Pressure Interval. The value rho_min is the density that is calculated at the existing temperature. An absolute pressure value as specified by the Cut-off Pressure, P_co.

Field Functions

The following table shows which field functions become available for which equation of state model:


	Ideal	IAPWS-w	TNEq	UDEOS
Compressibility Factor		✓
Critical Pressure		✓
Critical Temperature		✓
Enthalpy of [material]				✓
Entropy	✓	✓	✓
Entropy Function	✓		✓
Gas Constant	✓	✓	✓
IAPWS Region ID		✓
Mach Number	✓	✓	✓
Molecular Weight	✓	✓	✓
Ratio of Specific Heats	✓	✓	✓
Reduced Pressure		✓
Reduced Temperature		✓
Relative Mach Number	✓	✓	✓
Saturation Pressure		✓
Saturation Temperature		✓
Speed of Sound	✓	✓	✓

See Real Gas Models for the field functions of individual real gas models.

可压缩性因子

表示实际气体与理想气体的偏差量，表示为

Z = p / (ρ R T)

。通常，此因子取值大约为 1。

对于平衡空气模型，可压缩性因子表示离解度。这并非理想行为，但值的变化范围更广（大约介于 1 和 6 之间）。Eqn. (686) 中给出了平衡空气模型的简化公式。

临界压力

表示为

p_{c}

。

临界温度

表示为

T_{c}

。

[材料] 的焓

指定材料的焓。

Entropy

For the Ideal Gas model, the entropy

s

is calculated as:

图 3. EQUATION_DISPLAY

s = C_{p} ln (T / T_{r e f}) - R ln (P / P_{r e f})

(187)

图 4. EQUATION_DISPLAY

R ln (S) = C_{p} ln (T / T_{r e f}) - R ln (P / P_{r e f})

(188)

where:

$C_{p}$ is the specific heat.
$T$ is the temperature and $T_{r e f}$ is the reference temperature.
$P$ is the absolute pressure Pa and $P_{r e f}$ is the reference pressure.
$R$ is the specific gas constant.

Comparison of Eqn. (187) and Eqn. (188) shows that Entropy $s$ can be related to Entropy Function $S$ as follows:

图 5. EQUATION_DISPLAY

s = R ln (S)

(189)

where $T_{r e f} = 1 K$ and $P_{r e f} = 1 Pa$ . 

For the IAPWS-IF97 model, the entropy calculation follows the IAPWS-IF97 specification [25], [26], [27].

For the other equations of state, different formulas are used to ensure that the correct value for entropy is calculated and displayed in the field function.

The entropy value depends on the Specific Heat material property method that you use. If you change the Specific Heat method, the field function value changes accordingly.

The equation of state models use a reference temperature and a standard-state entropy. If these values are not specified, the defaults are used: the reference temperature is assumed to be 298.15 K and the standard-state entropy is assumed to be 0. In this case, negative entropy values are possible as a negative value implies entropy levels below the standard state level.

When you use thermodynamic polynomials to set the Specific Heat, the polynomials have a reference temperature and entropy built into the specification. These values are used to calculate entropy. Therefore, if you change to a different Specific Heat method, the entropy can be expected to jump due to the inclusion of a non-zero standard state entropy.

Entropy Function

The entropy function

S

is calculated as:

图 6. EQUATION_DISPLAY

S = \frac{{(T / T_{r e f})}^{(C_{p} / R)}}{(P / P_{r e f})}

(190)

This expression can be rewritten as:

图 7. EQUATION_DISPLAY

R ln (S) = C_{p} ln (T / T_{r e f}) - R ln (P / P_{r e f})

(191)

The entropy function measures the degree to which a flow is isentropic, with a value of 1 indicating isentropic flow.

气体常数

单位气体常数。

IAPWS 区域 ID

Simcenter STAR-CCM+ 针对特定的 IAPWS 有效区域计算的数据。

马赫数

局部马赫数。

分子量

为材料指定的分子量。

比热比

表示为：

$γ = \frac{C_{p}}{C_{v}} = \frac{C_{p}}{(C_{p} - R)}$

其中 $C_{p}$ 为比热 J/(kg K)， $R$ 为单位气体常数 J/(kg K)。

折算压力

表示为

p_{r} = p / p_{c}

。

折算温度

表示为

T_{r} = T / T_{c}

。

相对马赫数

饱和压力

为材料指定的饱和压力。

饱和温度

为材料指定的饱和温度。

声速

介质中的声音传播速率。