本书名为 Physics-Based Deep Learning (基于物理的深度学习)，意指将物理建模和数值模拟与基于人工神经网络的方法相结合。基于物理的深度学习的大方向代表了一个非常活跃、快速发展和令人兴奋的研究领域。接下来的章节将更详细地介绍这个主题，并为后续章节奠定基础。

图 4 了解我们的环境并预测其演化是人类面临的关键挑战之一。实现这些目标的一个重要工具是模拟，而下一代模拟将极大受益于整合深度学习组件，以便对我们的世界进行更准确的预测。

2.1 动机

从天气预报[Sto14]（见上图），到量子物理学[OMalleyBK+16]，再到等离子体聚变控制[MLA+19]，利用数值分析来获得物理模型的解已成为科学研究不可分割的一部分。近年来，机器学习技术尤其是深度神经网络在多个领域取得了令人瞩目的成就：从图像分类[KSH12]到自然语言处理[RWC+19]，以及最近的蛋白质折叠[Qur19]。该领域充满活力，发展迅速，前景广阔。

2.1.1 取代传统的模拟？

这些深度学习（DL）方法的成功案例引起了人们的关注，认为这种技术有可能取代传统的、模拟驱动的科学方法。例如，最近的研究表明，基于神经网络的代理模型达到了实际工业应用（如机翼流）所需的精度[CT21]，同时在运行时间方面优于传统求解器几个数量级。

我们是否可以不依赖于仔细设计的基于基础原理的模型，而是通过处理足够大的数据集来提供正确的答案呢？正如我们将在接下来的章节中展示的那样，这种担忧是没有根据的。相反，对于下一代模拟系统来说，将传统的数值技术与深度学习方法相结合是至关重要的。

这种组合的重要性有一个核心原因，那就是深度学习方法强大的同时，也能从物理模型形式的领域知识中获益匪浅。深度学习技术和神经网络都比较新颖，有时应用起来比较困难，诚然，将我们对物理过程的理解妥善地融入到深度学习算法中往往并非易事。

在过去的几十年中，人们已经开发出高度专业和精确的离散方法来求解如 Navier-Stokes、Maxwell 或 Schroedinger 方程等基本模型方程。对离散方法进行的看似微不足道的改动却能决定在计算结果中是否能够看到关键的物理现象。本书非但不会抛弃数值数学领域已开发出的强大方法，反而会说明在应用深度学习时尽可能使用这些方法大有裨益。

2.1.2 黑匣子和魔法？

不熟悉 DL 方法的人通常会将神经网络与 黑盒子 联系在一起，并将训练过程视为人类无法理解的东西。然而这些观点通常源于道听途说和对这一主题了解不够。

相反，这种情况在科学界很常见：我们正在面对一类新的方法，而 所有的细节 还没有完全解决。这种情况在各种科学进步中都很常见。数值方法本身就是一个很好的例子。1950 年前后，数值逼近和求解器的地位十分艰难。例如，引用 H. Goldstine 的说法，数值不稳定性被认为是 未来焦虑的持续来源[Gol90]。现在，我们已经很好地掌握了这些不稳定性，数值方法无处不在，而且已经非常成熟。

因此，我们必须意识到，从某种程度上说，深度学习方法并不神奇或超凡脱俗。它们只是另一套数值工具。尽管如此，它们显然还是相当新的工具，而且现在绝对是我们所拥有的用于解决非线性问题的最强大的工具集。不能因为所有的细节还没有完全解决，还没有写得很好，就阻止我们将这些强大的方法纳入我们的数值工具箱。

2.1.3 协调DL和模拟

退一步说，本书的目的是利用我们所掌握的所有强大的数值模拟技术，并将它们与深度学习结合起来使用。因此，本书的核心目标是将以数据为中心的观点与物理模拟重新结合起来。

我们将讨论的关键问题包括：

• 解释如何使用深度学习技术来求解PDE问题
• 如何将它们与现有的物理学知识结合起来
• 不抛弃我们已有的关于数值方法的知识。

与此同时，值得注意的是，我们不会涵盖的内容包括：

• 深度学习和数值模拟的介绍，我们不打算对这一领域的研究文章进行广泛的研究

由此产生的方法在改进数值方法方面具有巨大潜力：例如，在求解器重复求解某个定义明确的问题领域中的案例时，投入大量资源训练一个支持重复求解的神经网络就非常有意义。基于该网络的特定领域专用性，这种混合网络的性能会大大超过传统的通用求解器。尽管还有很多问题有待解决，但第一批出版物已经证明，这一目标并不遥远[KSA+21, UBH+20]。

另一种看法是，我们自然界的所有数学模型都是理想化的近似值，都包含误差。为了获得非常好的模型方程，我们已经付出了很多努力，但为了向前迈进一大步，DL 方法提供了一个非常强大的工具，可以缩小与现实的差距[AAC+19]。

2.2 分类

在基于物理的深度学习领域，我们可以区分出从目标约束、组合方法、优化到应用的各种不同方法。更具体地说，所有方法要么针对正向模拟（预测状态或时间演化），要么针对反向问题（例如，从观测结果中获取物理系统的参数）。

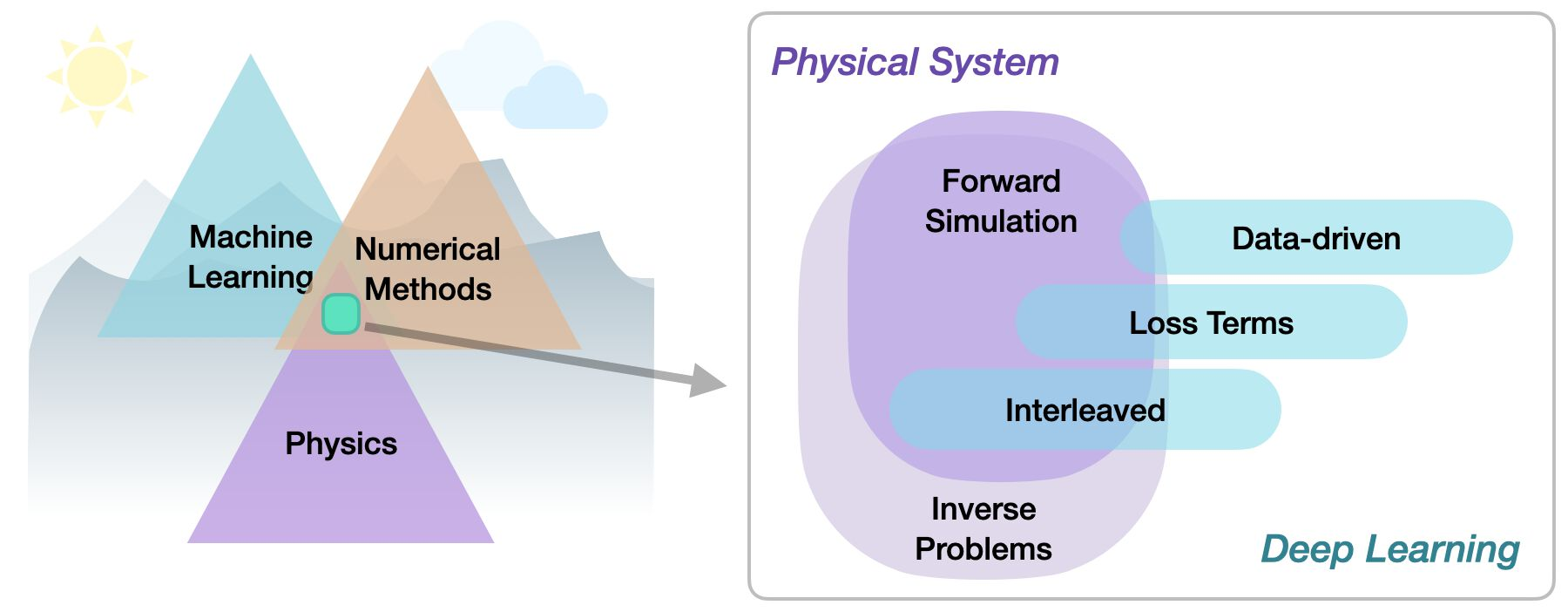
无论我们考虑的是正向问题还是反向问题，以下主题最关键的区别在于深度学习技术与领域知识（通常以偏微分方程（PDE）的形式）之间的整合方式的性质。基于物理学的深度学习（PBDL）技术大致可分为以下三类：

• 监督学习（Supervised:）：数据由物理系统（真实或模拟）产生，但不存在进一步的交互。这是典型的机器学习方法。
• 损失项（Loss-terms）：物理动力学（或其部分）通常以可微分算子的形式被编码在损失函数中。学习过程可以重复评估损失，并且通常从基于 PDE 的表达式中获得梯度。这些软约束有时也被称为“具有物理信息”的训练方法。
• 交织方法（Interleaved）：完整的物理模拟与深度神经网络的输出交织并结合在一起。这需要一个完全可微分的模拟器，代表了物理系统与学习过程之间最紧密的耦合。交织式可微分物理方法在时间演化中尤为重要，其可以为动力学的未来行为做出估计。

因此，可以根据正向求解与反向求解以及物理模型在训练深度神经网络的优化循环中的紧密程度进行分类。在这里，特别是利用“可微分物理”进行交织的方法允许深度学习和数值模拟方法之间的非常紧密的集成。

2.2.1 命名

值得指出的是，在接下来的内容中，我们所称谓的可微分物理学 (Differentiable Physics，DP）在其他资源和研究论文中有多种不同的名称。可微分物理学的名称受到深度学习中可微分编程范式的启发。在这里，例如我们还有可微分渲染方法，用于模拟光线如何形成我们作为人类所看到的图像。相比之下，我们将从现在开始专注于物理模拟，因此才有了这个名字。

然而，来自其他背景的人更常用其他名称。例如可微分物理方法等效于使用伴随方法（adjoint method），并将其与深度学习过程相结合。实际上，它也等效于将反向传播/反向模式微分应用于数值模拟。然而正如上面所提到的，出于对深度学习观点的考虑，从现在开始我们将统称这些方法为可微分物理方法。

2.3 展望未来

物理模拟是一个庞大的领域，我们无法涵盖所有可能的物理模型和模拟类型。

注意本书的重点在于：

• 基于场的模拟（没有拉格朗日方法）
• 与深度学习的结合（存在其他许多有趣的机器学习技术，但这里不讨论）
• 实验留作展望（即用真实世界的观测数据取代合成数据）

值得注意的是，我们正从一些非常基本的构建模块开始构建这些方法。以下是跳过后面章节的一些注意事项。

提示：如果满足以下条件，可以跳过...

• 非常熟悉数值方法和偏微分方程求解器，并且希望立即开始DL主题。那么监督训练章节是一个很好的起点。
• 另一方面，如果已经深入NNs&Co，并且想跳过研究相关主题，我们建议从物理损失项章节开始，这为下一章奠定了基础。

不过，在这两种情况下，简单了解一下我们在符号和缩写 章节中的 符号 并不会有什么坏处！

2.4 实现

这段文字还介绍了一系列深度学习和模拟API的概述。我们将使用流行的深度学习API，[如pytorch](https://pytorch.org]和 tensorflow，并且额外介绍了可微分模拟框架 Φ_Flow (phiflow) 。其中一些示例也使用了JAX。因此，通过学习这些示例，您应该对当前API中提供的功能有一个很好的概览，从而可以为新任务选择最适合的API。

由于我们（在大多数Jupyter笔记本示例中）处理的是随机优化问题，因此下面的许多代码示例每次运行时都会产生稍微不同的结果。这在神经网络训练中非常常见，但在执行代码时要牢记这一点。这也意味着文本中讨论的数字可能与您重新运行示例后看到的数字并不完全一致。

2.5 模型与方程

下面我们将简要介绍深度学习（真的是非常非常简要！），主要是为了介绍符号表示法。

此外，我们将在下面讨论一些模型方程。请注意，与其他一些文本和API不同，我们将避免使用Model来表示经过训练的神经网络。它们将被称为NNs（神经网络）或networks（网络）。这里的Model（模型）通常表示一组描述物理效应的模型方程，它们通常是偏微分方程（PDEs）。

2.5.1 深度学习与神经网络

在本书中，我们专注于与物理模型的联系，而深度学习有很多很棒的介绍。因此，我们将保持简短：深度学习的目标是近似一个未知函数： $$f^{\ast }(x)=y^{\ast }\text{\hspace{1em}(1)}$$ 其中，$y^{\ast }$ 表示参考解或真实解。$f^{\ast }(x)$应该用NN表示$f(x;\theta )$来近似。我们通常借助损失函数 $L(y,y^{\ast })$的某种变体来确定 $f$，其中 $y=f(x;\theta )$ 是 NN 的输出。这就给出了一个最小化问题，即找到 $f(x;\theta )$使得 $e$ 最小化。在最简单的情况下，我们可以使用 $L^2$ 误差，得出 $$\arg \underset{\theta }{\min }{\left|f(x;\theta )-y^{\ast }\right|}_2^2\text{\hspace{1em}(2)}$$ 通常，我们使用随机梯度下降（SGD）优化器（例如Adam [KB14]）对其进行优化，即训练。我们将依赖于自动微分来计算损失函数$L$相对于权重$\theta$的梯度$\partial L/\partial \theta$。对于梯度计算来说，这个函数是标量且非常重要，损失函数通常也被称为误差函数、成本函数或目标函数。

对于训练，我们要区分：从某种分布中提取的训练数据集、验证数据集（来自相同的分布，但数据不同），以及与训练数据集有某种不同分布的测试数据集。后一种区别非常重要。对于测试集，我们需要 超出分布范围（OOD）的数据，以检查训练模型的泛化效果。需要注意的是，这就为测试数据集提供了一个巨大的可能性范围：从肯定会起作用的微小变化，到基本上保证会失败的完全不同的输入。虽然没有黄金标准，但在生成测试数据时仍需谨慎。

如果以上内容对你来说还不够明显，我们强烈建议阅读《深度学习》这本书的第6章至第9章，尤其是关于多层感知器（MLPs）和卷积神经网络（CNNs）的部分。你可以在深度学习的链接中找到这些章节，分别是MLPs和Conv-Nets，即卷积神经网络（CNNs）。

分类问题和回归问题之间的经典 ML 区别在这里并不重要：下面的内容中，我们只讨论回归问题。

2.5.2 作为物理模型的偏微分方程

接下来的部分将简要介绍稍后在深度学习示例中所使用到的一些模型方程。我们的目标通常是连续的偏微分方程，用 ${\mathcal{P}}^{\ast }$ 表示，其解处在 $d\in 1,2,3$ 维的空间域 $\Omega \subset {\mathbb{R}}^d$ 中。此外我们还经常考虑方程在有限时间间隔 $t\in {\mathbb{R}}^{+}$ 内的演化过程。相应的物理场可以是 d 维向量场，例如 $\mathbf{u}：{\mathbb{R}}^d\times {\mathbb{R}}^{+}\to {\mathbb{R}}^d$，也可以是标量场 $\mathbf{p}：{\mathbb{R}}^d\times {\mathbb{R}}^{+}\to \mathbb{R}$。向量的分量通常用$x，y，z$下标表示，即$\mathbf{v}=(v_x，v_y，v_z{)}^T$（当$d=3$时），而位置则用$x\in \Omega$表示。

为了得到 ${\mathcal{P}}^{\ast }$ 的唯一解，我们需要指定合适的初始条件，通常是在 $t=0$ 时的所有相关物理量，以及 $\Omega$ 边界的边界条件，在下文中用 $\Gamma$ 表示。

${\mathcal{P}}^{\ast }$ 表示一个连续的公式，我们对其连续性做了轻微的假设，通常我们会假设其存在一阶导数和二阶导数。

然后，我们可以使用数值方法，通过离散化获得平滑函数的近似值，如 ${\mathcal{P}}^{\ast }$。这必然会引入离散化误差，我们希望误差越小越好。这些误差可以用与精确分析解的偏差来衡量，对于离散模拟 PDEs，它们通常表示为截断误差 $O(\Delta x^k)$ 的函数，其中 $\Delta x$ 表示离散化的空间步长。同样，我们通常通过时间步长 $\Delta t$ 进行时间离散化。

我们通过执行大小为 $\Delta t$ 的步长来求解一个离散的偏微分方程$\mathcal{P}$。解可以表示为 $\mathbf{u}$ 及其导数的函数：$\mathbf{u}(\mathbf{x}，t+\Delta t)=\mathcal{P}\left({\mathbf{u}}_x，{\mathbf{u}}_{xx}，\dots {\mathbf{u}}_{xx\dots x}\right)$，其中 ${\mathbf{u}}_x$ 表示空间导数 $\partial \mathbf{u}(\mathbf{x},t)/\partial \mathbf{x}$。

接下来，我们将对模型方程进行概述，然后在后续章节及性能实际模拟和实现示例。

2.5.3 一些PDE示例

以下PDEs是很好的例子，我们将在不同的设置中使用它们来展示如何将它们纳入到深度学习中。

Burgers方程

我们经常以一维或二维的Burgers方程作为起点。这是一个经过广泛研究的偏微分方程，与Navier-Stokes方程不同，该方程不包含任何额外的约束条件（如质量守恒）。因此，它会导致有趣的激波形成。Burgers方程包含一个对流项（运动/输运）和一个扩散项（由热力学第二定律引起的耗散）。

二维Burgers方程表示为： $$\begin{array}{l}\frac{\partial u_x}{\partial t}+\mathbf{u}\cdot \nabla u_x=\nu \nabla \cdot \nabla u_x+g_x\\ \frac{\partial u_y}{\partial t}+\mathbf{u}\cdot \nabla u_y=\nu \nabla \cdot \nabla u_y+g_y\end{array}\text{\hspace{1em}(3)}$$ 式中，$\nu$及$\mathbf{g}$分别表示扩散常数和外力。

在没有外力的情况下，，将单个一维速度分量表示为$u=u_x$，可以得到burgers方程在一维空间中简单的变体： $$\frac{\partial u}{\partial t}+u\nabla u=\nu \nabla \cdot \nabla u\text{\hspace{1em}(4)}$$ Navier-Stokes方程

就复杂性而言，Navier-Stokes方程是一个很好的下一步，它是一个成熟的流体模型。除了动量守恒方程（类似于Burgers方程）外，该方程还包括质量守恒方程。这可以防止激波的形成，但同时为数值方法引入了新的挑战，即添加了无散度运动的硬约束条件。

在二维情况下，没有任何外部力的Navier-Stokes方程可以写成： $$\begin{array}{rl}\frac{\partial u_x}{\partial t}+\mathbf{u}\cdot \nabla u_x& =-\frac{\Delta t}{\rho }\nabla p+\nu \nabla \cdot \nabla u_x\\ \frac{\partial u_y}{\partial t}+\mathbf{u}\cdot \nabla u_y& =-\frac{\Delta t}{\rho }\nabla p+\nu \nabla \cdot \nabla u_y\\ \nabla \cdot \mathbf{u}& =0\end{array}\text{\hspace{1em}(5)}$$ 其中，像前面一样，𝜈 为粘度。

NS方程一个有趣的变体是通过包含Boussinesq近似来考虑温度对流体密度的影响。使用一个标记场$v$来指示高温区域，可以得到以下方程组： $$\begin{array}{rl}\frac{\partial u_x}{\partial t}+\mathbf{u}\cdot \nabla u_x& =-\frac{\Delta t}{\rho }\nabla p\\ \frac{\partial u_y}{\partial t}+\mathbf{u}\cdot \nabla u_y& =-\frac{\Delta t}{\rho }\nabla p+\xi v\\ \mathrm{subject}\mathrm{to}\nabla \cdot \mathbf{u}& =0\\ \frac{\partial v}{\partial t}+\mathbf{u}\cdot \nabla v& =0\end{array}\text{\hspace{1em}(6)}$$ 其中𝜉表示浮力的强度。

最后，3D中的Navier-Stokes模型给出了以下方程组： $$\begin{array}{rl}\frac{\partial u_x}{\partial t}+\mathbf{u}\cdot \nabla u_x& =-\frac{\Delta t}{\rho }\nabla p+\nu \nabla \cdot \nabla u_x\\ \frac{\partial u_y}{\partial t}+\mathbf{u}\cdot \nabla u_y& =-\frac{\Delta t}{\rho }\nabla p+\nu \nabla \cdot \nabla u_y\\ \frac{\partial u_z}{\partial t}+\mathbf{u}\cdot \nabla u_z& =-\frac{\Delta t}{\rho }\nabla p+\nu \nabla \cdot \nabla u_z\\ \mathrm{subject}\mathrm{to}\nabla \cdot \mathbf{u}& =0\end{array}\text{\hspace{1em}(7)}$$

2.5.4 正向模拟

在我们真正开始学习方法之前，有必要介绍一下使用上述模型方程的最基本的变体：常规的 正向 模拟，即从一组初始条件开始，随着时间的推移，用模型方程的离散版本演化系统的状态。我们将展示如何对一维burgers方程和二维的Navier-Stokes模拟进行这种正向模拟。

2.6 用phiflow对Burgers方程进行正演模拟

本章将介绍如何运行“正向”即常规模拟，即从给定的初始状态开始，通过数值逼近来近似后续状态，并介绍Φ_Flow框架。Φ_Flow提供了一组可微分的构建模块，可以直接与深度学习框架进行接口，因此非常适合本书的主题。在深入和更复杂的集成之前，本章（以及下一章）将展示如何使用Φ_Flow进行常规模拟。随后，我们将展示如何轻松将这些模拟与神经网络进行耦合。

ΦFlow的主要代码库（以下简称为"phiflow"）位于https://github.com/tum-pbs/PhiFlow，您可以在https://tum-pbs.github.io/PhiFlow/找到其他API文档和示例。

对于这个jupyter笔记本（以及后续的笔记本），你可以在第一个段落的末尾找到一个“[在Colab中运行]”的链接（或者你可以使用页面顶部的启动按钮）。这将在Colab中加载PBDL GitHub仓库中的最新版本的笔记本，你可以立即执行它：在Colab中运行。

2.6.1 Model

我们使用Burgers方程作为物理模型。这个方程是一个非常简单、非线性且非平凡的模型方程，可以导致有趣的冲击波形成。因此它是我们进行实验的一个很好的起点，该方程的一维版本（方程(4)）如下所示： $$\frac{\partial u}{\partial t}+u\nabla u=\nu \nabla \cdot \nabla u$$

2.6.2 导入和加载Phiflow

让我们先做一些准备工作：首先，我们将导入phiflow库，更具体地说是用于流体模拟的numpy运算符：phi.flow（用于DL框架X的可微分版本则通过phi.X.flow加载）。

注意： 下面的第一条带有"!"前缀的命令将通过pip在您的Python环境中安装来自GitHub的phiflow Python包。我们假设您尚未安装phiflow，但如果您已经安装了，请注释掉第一行（对于后续的所有笔记本也是如此）。

!pip install --upgrade --quiet phiflow==2.2
from phi.flow import *

注意：这里如果提示dtype错误，则需要修改C:\ProgramData\anaconda3\Lib\site-packages\phi\math\backend_dtype.py文件，修改第135行为 DType(object): np.dtype('O'),，修改第139行为_FROM_NUMPY[np.bool_] = DType(bool)。主要原因是numpy升级后抛弃了np.object及np.bool。如果是低版本的numpy则不会报错。

接下来，可以定义并初始化必要的常量（用大写字母表示）：模拟域具有N=128个单元格作为1D速度$u$的离散点，这些离散点位于在周期性域$\Omega$上的区间$[-1,1]$内。我们将使用32个时间步长STEPS，时间间隔为1，因此我们得到DT=1/32。此外，我们将使用粘度NU为$\nu =0.01/\pi$。

我们还将定义一个初始状态，由numpy数组INITIAL_NUMPY中的$-\text{sin}(\pi x)$给出，我们将在下一个单元格中使用它来初始化模拟中的速度$u$。此初始化将在计算域的中心产生一个漂亮的冲击波。

Phiflow是面向对象的，以场数据形式（由张量对象在内部表示）为中心。也就是说，您通过构建一些网格来组装模拟，并在时间步长内更新它们。

Phiflow在内部使用带有命名维度的张量。这在后面处理具有附加批处理和通道维度的2D模拟时将非常方便，但现在我们只需将1D数组简单地转换为具有单个空间维度'x'的phiflow张量即可。

N = 128
DX = 2./N
STEPS = 32
DT = 1./STEPS
NU = 0.01/(N*np.pi)
# initialization of velocities， cell centers of a CenteredGrid have DX/2 offsets for linspace()
INITIAL_NUMPY = np.asarray( [-np.sin(np.pi * x) for x in np.linspace(-1+DX/2，1-DX/2，N)] ) # 1D numpy array
INITIAL = math.tensor(INITIAL_NUMPY， spatial('x') ) # convert to phiflow tensor

接下来，我们从转换为张量的INITIAL numpy数组中初始化一个1D velocity 网格。 我们通过bounds参数$[-1,1]$来指定域$\Omega$的范围，并且网格使用周期性边界条件（extrapolation.PERIODIC）。这两个属性是张量和网格之间的主要区别：后者具有边界条件和物理范围。

为了便于说明，我们还将输出有关速度对象的一些信息：它是一个大小为128的phi.math张量。请注意，实际的网格内容包含在网格的values中。下面我们使用numpy()函数将phiflow张量的内容转换为numpy数组，并输出其中的五个条目。对于具有更多维度的张量，我们需要在这里指定额外的维度，例如，对于一个2D速度场，我们会使用'y,x,vector'（对于只有单个维度的张量，我们可以省略它）。

velocity = CenteredGrid(INITIAL， extrapolation.PERIODIC， x=N， bounds=Box('x'，-1:1))
vt = advect.semi_lagrangian(velocity， velocity， DT)
print(`Velocity tensor shape: ` + format( velocity.shape )) # == velocity.values.shape
print(`Velocity tensor type: ` + format( type(velocity.values) ))
print(`Velocity tensor entries 10 to 14: ` + format( velocity.values.numpy('x')[10:15] ))

输出结果为：

Velocity tensor shape: (x=128)
Velocity tensor type: <class 'phi.math._tensors.CollapsedTensor'> 
Velocity tensor entries 10 to 14: [0.49289819 0.53499762 0.57580819 0.61523159 0.65317284]

2.6.3 运行模拟

现在我们可以准备运行模拟了。为了计算模型方程中的扩散和对流分量，我们可以简单地调用phiflow中现有的diffusion和semi_lagrangian运算符：diffuse.explicit(u,...)通过中心差分计算模型中项$\nu \nabla \cdot \nabla u$的显式扩散。接下来，advect.semi_lagrangian(f,u)用于通过速度u对任意场f进行稳定的一阶逼近输运。在模型中有$\partial u/\partial t+u\nabla f$，因此可以使用semi_lagrangian函数在实现中将速度与自身进行输运：

velocities = [velocity]
age = 0.
for i in range(STEPS):
    v1 = diffuse.explicit(velocities[-1]， NU， DT)
    v2 = advect.semi_lagrangian(v1， v1， DT)
    age += DT
    velocities.append(v2)
print(`New velocity content at t={}: {}`.format( age， velocities[-1].values.numpy('x，vector')[0:5] ))

输出结果为：

New velocity content at t=1.0: [[0.0057228 ]
[0.01716715]
[0.02861034]
[0.040052 ]
[0.05149214]]

在这里，我们实际上将所有时间步收集到列表velocities中。一般来说，这并不是必需的（并且对于长时间运行的模拟可能会消耗大量内存），但在这里可以用于后续速度状态演变的绘制。

print语句输出了一些速度值，已经表明我们的模拟正在发生一些事情，但很难从这些数字中直观地了解 PDE 的行为。因此，让我们将随时间变化的状态可视化，以显示正在发生的事情。

2.6.4 可视化

我们可以很容易地通过图表直观地看到这种一维情况：下面的代码用蓝色显示初始状态，然后用绿色、青色和紫色显示 $10/32,20/32,1$ 的时间。

# get `velocity.values` from each phiflow state with a channel dimensions， i.e. `vector`
vels = [v.values.numpy('x，vector') for v in velocities] # gives a list of 2D arrays

import pylab

fig = pylab.figure().gca()
fig.plot(np.linspace(-1，1，len(vels[ 0].flatten()))， vels[ 0].flatten()， lw=2， color='blue'， label=`t=0`)
fig.plot(np.linspace(-1，1，len(vels[10].flatten()))， vels[10].flatten()， lw=2， color='green'， label=`t=0.3125`)
fig.plot(np.linspace(-1，1，len(vels[20].flatten()))， vels[20].flatten()， lw=2， color='cyan'， label=`t=0.625`)
fig.plot(np.linspace(-1，1，len(vels[32].flatten()))， vels[32].flatten()， lw=2， color='purple'，label=`t=1`)
pylab.xlabel('x'); pylab.ylabel('u'); pylab.legend()

输出结果如图所示。

这很好地显示了在我们的区域中心形成的激波，它是由两个初始速度 凸起（左侧的正凸起（向右移动）和中心右侧的负凸起（向左移动））碰撞形成的。

由于这些线条可能会有很多重叠，我们在接下来的章节中还将使用另一种可视化方法，即在二维图像中显示所有时间步长的演变过程。我们的一维域将沿 Y 轴显示，沿 X 轴的每个点代表一个时间步长。

下面的代码将我们的速度状态集合转换为二维数组，将单个时间步长重复 8 次，以使图像更宽。当然，这完全是可有可无的，但却能让我们更容易地看到汉堡模拟中发生的事情。

import os
def show_state(a， title):

    # we only have 33 time steps， blow up by a factor of 2^4 to make it easier to see
    # (could also be done with more evaluations of network)
    a = np.expand_dims(a， axis=2)
    for i in range(4):
        a = np.concatenate([a， a]， axis=2)
    a = np.reshape(a， [a.shape[0]， a.shape[1]*a.shape[2]])
    #print(`Resulting image size` +format(a.shape))
    fig， axes = pylab.subplots(1， 1， figsize=(16， 5))
    im = axes.imshow(a， origin='upper'， cmap='inferno')
    pylab.colorbar(im)
    pylab.xlabel('time')
    pylab.ylabel('x')
    pylab.title(title)

vels_img = np.asarray(np.concatenate(vels， axis=-1)， dtype=np.float32)
# save for comparison with reconstructions later on
os.makedirs(`./temp`， exist_ok=True)
np.savez_compressed(`./temp/burgers-groundtruth-solution.npz`，np.reshape(vels_img， [N， STEPS+1]))

show_state(vels_img， `Velocity`)

运行结果为：

至此，phiflow 的首次模拟结束。它并不太复杂，但正因为如此，它为下一章评估和比较不同的基于物理的深度学习方法提供了一个良好的起点。不过在此之前，我们将在下一节针对更复杂的模拟类型进行研究。

2.6.5 后续步骤

在此模拟设置的基础上进行一些尝试：

• 请随意尝试 - 上述设置非常简单，您可以更改模拟参数或初始化。例如，可以通过 Noise() 使用噪声场来获得更混乱的结果（参见上文 速度 单元中的注释）。
• 更复杂一点：将模拟扩展到 2D（或更高）。这需要对整个程序进行修改，但上述所有运算符都支持更高维度。在尝试之前，您可能需要查看下一个示例，它涵盖了一个 2D Navier-Stokes 案例。

2.7 Navier-Stokes 正向模拟

现在让我们举一个更复杂的例子：基于纳维-斯托克斯方程的流体模拟。使用 Φ_Flow (phiflow)仍然非常简单，因为这里存在所有步骤的可微分算子。纳维-斯托克斯方程（不可压缩形式）引入了额外的压力场 $p$，以及质量守恒约束。我们还将随着气流移动一个标记场，这里用 $d$ 表示。它表示温度较高的区域，并通过浮力因子$\xi$产生作用力： $$\begin{array}{rl}\frac{\partial \mathbf{u}}{\partial t}+\mathbf{u}\cdot \nabla \mathbf{u}& =-\frac{1}{\rho }\nabla p+\nu \nabla \cdot \nabla \mathbf{u}+(0,1{)}^T\xi d\text{s.t.}\nabla \cdot \mathbf{u}=0,\\ \frac{\partial d}{\partial t}+\mathbf{u}\cdot \nabla d& =0\end{array}$$

在这里，我们的目标是无压缩流 (即 $\rho =\text{const}$)， 并通过项 $(0，1{)}^T\xi d$ 使用一个简单的浮力模型 (Boussinesq 近似)。这在不显式计算 $\rho$ 的情况下为无压缩求解器近似了密度的变化。我们假设一个沿 y 方向作用的重力力， 通过向量 $(0，1{)}^T$。

我们将在一个封闭域上求解这个 PDE，该域的速度边界条件为 $\mathbf{u}=0$，压力边界条件为 $\frac{\partial p}{\partial x}=0$，该域的物理尺寸为 $100\times 80$ 单位。[run in colab]

2.7.1 实现

与上一节一样，第一条带!前缀的命令是在 python 环境中通过pip安装来自 GitHub 的 phiflow python 软件包。(如有必要，可跳过或修改此命令）。

from phi.flow import *  # The Dash GUI is not supported on Google colab, ignore the warning
import pylab

2.7.2 设置模拟

下面的代码会设置一些常数，这些常数用大写字母表示。我们将使用 $40\times 32$ 单元来离散域，通过 $\nu$ 引入轻微的粘性，并定义时间步长为 $\Delta t=1.5$。

我们首先创建一个 CenteredGrid，它由一个 Sphere 几何对象初始化。这将表示热烟雾生成的入流区域 INFLOW。

DT = 1.5
NU = 0.01

INFLOW = CenteredGrid(Sphere(center=tensor([30,15], channel(vector='x,y')), radius=10), extrapolation.BOUNDARY, x=32, y=40, bounds=Box(x=(0,80),y=(0,100))) * 0.2

流入的烟雾将被注入第二个居中的网格 smoke 中，该网格代表上面的标记字段 $d$。请注意，我们在上面定义了一个大小为 $100\times 80$ 的 Box。这是在我们的模拟中以空间单位表示的物理尺度，也就是说，$1$ 的速度将使烟雾密度每 1 个时间单位移动 1 个单位，这可能大于或小于离散网格中的一个单元，具体取决于 x,y 的设置。您可以将模拟网格参数设置为直接类似于现实世界的单位，或者考虑适当的换算因子。

上面的入流球体已经使用“世界”坐标: 它位于第一个轴上的 $x=30$， $y=15$ (在 $100\times 80$ 的域框内)。

接下来，我们为要模拟的量创建网格。在本例中，我们需要速度场和烟雾密度场。

smoke = CenteredGrid(0, extrapolation.BOUNDARY, x=32, y=40, bounds=Box(x=(0,80),y=(0,100)))  # sampled at cell centers
velocity = StaggeredGrid(0, extrapolation.ZERO, x=32, y=40, bounds=Box(x=(0,80),y=(0,100)))  # sampled in staggered form at face centers 

我们以交错形式对单元中心的烟场和速度进行采样。交错网格内部包含 2 个不同维度的居中网格，可通过 unstack 函数转换为居中网格（或简单的 numpy 数组），如上文链接中所述。

接下来，我们定义模拟的更新步骤，调用必要的函数将流体系统的状态向前推进 dt。下一个单元将计算一个这样的步骤，并绘制一个模拟帧后的标记密度图。

def step(velocity, smoke, pressure, dt=1.0, buoyancy_factor=1.0):
    smoke = advect.semi_lagrangian(smoke, velocity, dt) + INFLOW
    buoyancy_force = (smoke * (0, buoyancy_factor)).at(velocity)  # resamples smoke to velocity sample points
    velocity = advect.semi_lagrangian(velocity, velocity, dt) + dt * buoyancy_force
    velocity = diffuse.explicit(velocity, NU, dt)
    velocity, pressure = fluid.make_incompressible(velocity)
    return velocity, smoke, pressure

velocity, smoke, pressure = step(velocity, smoke, None, dt=DT)

print(`Max. velocity and mean marker density: ` + format( [ math.max(velocity.values) , math.mean(smoke.values) ] ))

pylab.imshow(np.asarray(smoke.values.numpy('y,x')), origin='lower', cmap='magma')

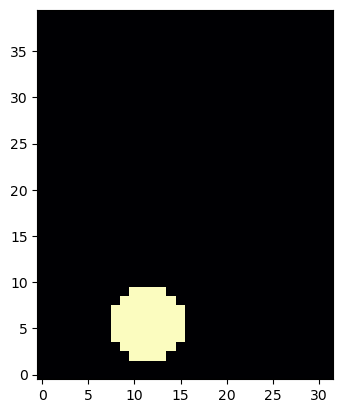
在这个 step() 调用中发生了很多事情：我们平移了烟场，通过Boussinesq 模型添加了一个向上的力，平移了速度场，最后通过压力求解使其无发散。

布尔辛斯克模型使用(0, buoyancy_factor) 元组乘法将烟场转化为交错的 2 分力场，并通过 at() 函数在速度分量的位置进行采样。该函数可确保交错速度分量的各个力分量被正确插值。请注意，这也会直接确保保留原始网格的边界条件。它还会在内部对生成的力网格执行 StaggeredGrid(..., extrapolation.ZERO,...) 内插。

在 make_incompressible 中的压力投影步骤通常是上述序列中计算成本最高的步骤。它根据域的边界条件求解泊松方程，并根据计算出的压力梯度更新速度场。

为了测试，我们还打印了更新后的速度平均值和最大密度。从生成的图像中可以看到，第一轮烟雾区域有轻微的向上运动（此处尚未显示）。

2.7.3 数据类型和尺寸

我们在这里为模拟字段创建的变量是Grid 类的实例。与张量一样，网格也有 shape 属性，该属性列出了所有批次、空间和通道维度。phiflow中的形状不仅存储了维度的大小，还存储了它们的名称和类型。

print(f"Smoke: {smoke.shape}")
print(f"Velocity: {velocity.shape}")
print(f"Inflow: {INFLOW.shape}, spatial only: {INFLOW.shape.spatial}")

请注意，这里的 phiflow 输出显示了维度的类型，例如，${}^S$ 表示空间维度，${}^V$ 表示向量维度。在后面的学习中，我们还将引入批量维度。

我们可以通过 .sizes获取形状对象的实际内容，或者通过 .get_size('dim')查询特定维度 dim 的大小。下面是两个示例：

print(f"Shape content: {velocity.shape.sizes}")
print(f"Vector dimension: {velocity.shape.get_size('vector')}")

可以使用 values 属性访问网格值。这是与 phiflow 张量对象的一个重要区别，后者没有values，如下代码示例所示。

print("Statistics of the different simulation grids:")
print(smoke.values)
print(velocity.values)

# in contrast to a simple tensor:
test_tensor = math.tensor(numpy.zeros([3, 5, 2]), spatial('x,y'), channel(vector="x,y"))
print("Reordered test tensor shape: " + format(test_tensor.numpy('vector,y,x').shape) ) # reorder to vector,y,x 
#print(test_tensor.values.numpy('y,x')) # error! tensors don't return their content via ".values"

网格还有更多的特性，这里 有详细记录。还要注意的是，交错网格具有非均匀形状，因为网格面的数量与单元格的数量不相等（在本例中，x 部分的单元格数量是 40 的 31 次方，而 y 部分的单元格数量是 39 的 32 次方）。INFLOW "网格的尺寸自然与 "smoke "网格相同。

2.7.4 时间演化

有了这种设置，我们就可以通过反复调用 step 函数，轻松地将模拟时间向前推进一些。

for time_step in range(10):
    velocity, smoke, pressure = step(velocity, smoke, pressure, dt=DT)
    print('Computed frame {}, max velocity {}'.format(time_step , np.asarray(math.max(velocity.values)) ))

现在，热羽流开始上升：

pylab.imshow(smoke.values.numpy('y,x'), origin='lower', cmap='magma')

让我们再计算并展示几个模拟步骤。由于流入的水流偏离中心向左（X 位置为 30），因此当羽流撞击到域的顶壁时会向右弯曲。

steps = [[ smoke.values, velocity.values.vector[0], velocity.values.vector[1] ]]
for time_step in range(20):
  if time_step<3 or time_step%10==0: 
    print('Computing time step %d' % time_step)
  velocity, smoke, pressure = step(velocity, smoke, pressure, dt=DT)
  if time_step%5==0:
    steps.append( [smoke.values, velocity.values.vector[0], velocity.values.vector[1]] )

fig, axes = pylab.subplots(1, len(steps), figsize=(16, 5))
for i in range(len(steps)):
    axes[i].imshow(steps[i][0].numpy('y,x'), origin='lower', cmap='magma')
    axes[i].set_title(f"d at t={i*5}")

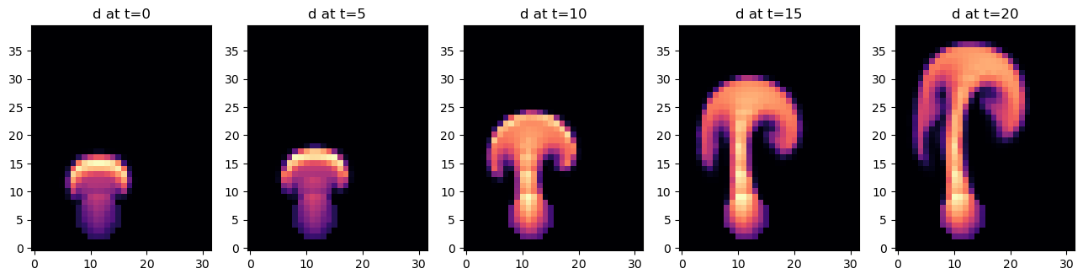
我们还可以看看速度。上面的 steps 列表已经将速度的 vector[0] 和 vector[1] 分量存储为 numpy 数组，接下来我们可以展示一下。

fig, axes = pylab.subplots(1, len(steps), figsize=(16, 5))
for i in range(len(steps)):
    axes[i].imshow(steps[i][1].numpy('y,x'), origin='lower', cmap='magma')
    axes[i].set_title(f"u_x at t={i*5}")
    
fig, axes = pylab.subplots(1, len(steps), figsize=(16, 5))
for i in range(len(steps)):
    axes[i].imshow(steps[i][2].numpy('y,x'), origin='lower', cmap='magma')
    axes[i].set_title(f"u_y at t={i*5}")

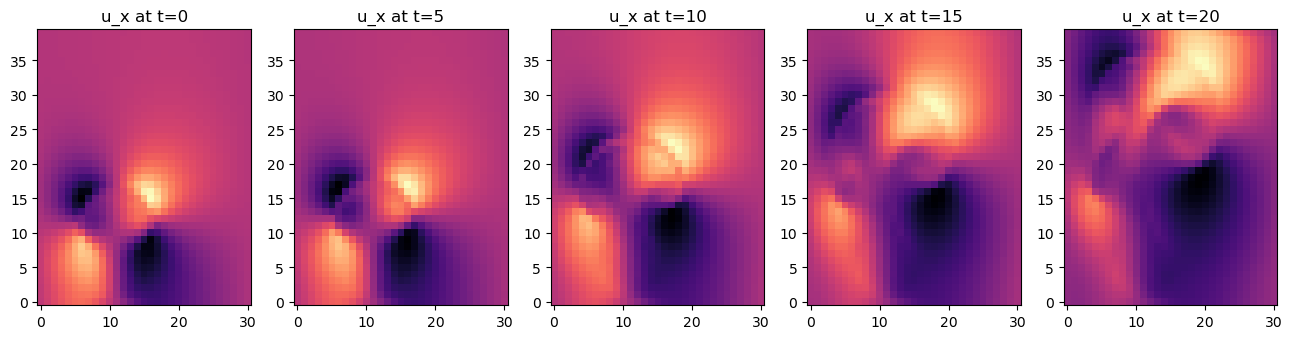
这里看起来很简单，但这个模拟设置却是一个功能强大的工具。仿真可以很容易地扩展到更复杂的情况或三维空间，而且它已经与深度学习框架的反向传播管道完全兼容。

在接下来的章节中，我们将展示如何使用这些模拟来训练 NN，以及如何通过训练好的 NN 来引导和修改它们。这将说明通过在循环中加入求解器，我们可以在多大程度上改进训练过程，尤其是当求解器是可变的时候。在进入这些更复杂的训练过程之前，我们将在下一章介绍一种更简单的监督方法。这一点非常重要：即使是针对基于物理的高级学习设置，有效的监督训练始终是第一步。

2.7.5 下一步

您可以在此基础上创建各种流体模拟。例如，尝试改变空间分辨率、浮力系数和模拟运行的总长度。

2.8 优化和收敛性

本章将概述不同优化算法的推导过程。与其他文章不同的是，我们将从牛顿法这一经典优化算法入手，推导出几种广泛使用的变体，然后再回到深度学习（DL）优化器。我们的主要目标是将 DL 纳入这些经典方法的范畴。虽然我们将专注于 DL，但我们也会在本书稍后部分重温经典算法，以改进学习算法。物理模拟夸大了神经网络造成的困难，这就是为什么下面的主题与基于物理的学习任务特别相关。

2.8.1 符号

本章使用一种自定义符号，这种符号经过精心挑选，可以清晰简要地表示所考虑的所有方法。我们有一个标量损失函数 $L(x)：{\mathbb{R}}^N\to \mathbb{R}$，最佳值（$L$ 的最小值）位于位置 $x^{\ast }$，$\Delta$ 表示在 $x$ 中的一个步。$x$中不同的中间更新步用下标表示，如$x_n$或$x_k$。

本章使用经过仔细选择的自定义符号， 以清晰简洁地表示正在考虑的所有方法。我们有一个标量损失函数 $L(x):{\mathbb{R}}^N\to \mathbb{R}$，最优点 (L 的最小值)在 $x^{\ast }$ 处， $\Delta$ 表示 $x$ 中的一步。 $x$ 中的不同中间更新步骤用下标表示， 例如 $x_n$ 或 $x_k$。

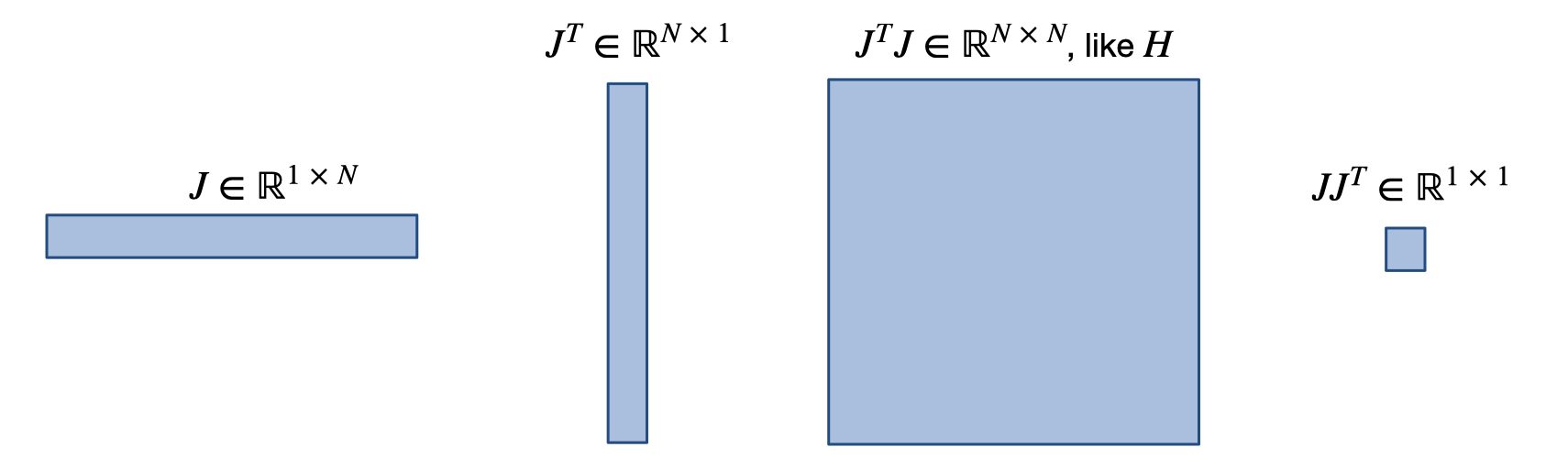
在下文中，我们经常需要取反，即除以某个量。对于矩阵 $A$ 和 $B$，我们定义 $\frac{A}{B}\equiv B^{-1}A$。当 $a$ 和 $b$ 是向量时，结果就是用下面两种公式之一得到的矩阵。我们将具体说明使用哪一种： $$\frac{a}{b}\equiv \frac{a{a}^T}{a^{T}b}\text{ 或 }\frac{a}{b}\equiv \frac{a{b}^T}{b^{T}b}$$

将 $/partial//partialx$ 应用于 $L$ 一次，可以得到雅各布值 $J(x)$。由于 $L$ 是标量，$J$ 是行向量，梯度（列向量）$\nabla L$ 由 $J^T$ 给出。再次应用 $\partial /\partial x$ 可以得到 Hessian 矩阵 $H(x)$，再次应用 $\partial /\partial x$ 可以得到第三导数张量，用 $K(x)$ 表示。幸运的是，我们从来不需要把 $K$ 作为一个完整的张量来计算，但在下面的一些推导中需要用到它。为了缩短下面的符号，当函数或导数在 $x$ 处求值时，我们通常会去掉 $(x)$，例如，$J$ 将表示为 $J(x)$。

下图概述了一些常用量的矩阵形状。之后我们就不需要它了，但在本图中，$N$表示$x$的维度，即$x\in {\mathbb{R}}^N$。

2.8.2 准备工作

我们需要一些工具来进行下面的推导，现将其总结如下，以供参考。

毫不奇怪，我们需要一些泰勒级数展开式。用上面的符号表示为 $$L(x+\Delta )=L+J\Delta +\frac{1}{2}H{\Delta }^2+\cdots$$

然后，我们还需要拉格朗日形式，它可以从区间 $[x,x+\Delta ]$ 中得到 $\xi$ 的精确解：

$$L(x+\Delta )=L+J\Delta +\frac{1}{2}H(\xi ){\Delta }^2$$

在一些情况下，我们会用到微积分基本定理，为了完整起见，在此重复一遍：

$$f(x+\Delta )=f(x)+{\int }_0^1\text{d}s{f}^{\prime }(x+s\Delta )\Delta .$$

此外，我们还将利用具有常数 $\mathcal{L}$ 的 Lipschitz连续性： $|f(x+\Delta )+f(x)|\le \mathcal{L}\Delta$，以及著名的 Cauchy-Schwartz 不等式：$u^{T}v<|u|\cdot |v|$。

2.8.3 牛顿法

现在，我们可以从最经典的优化算法开始：牛顿法它是通过将我们感兴趣的函数近似为抛物线而得出的。这是因为几乎所有的最小值近看都像抛物线。

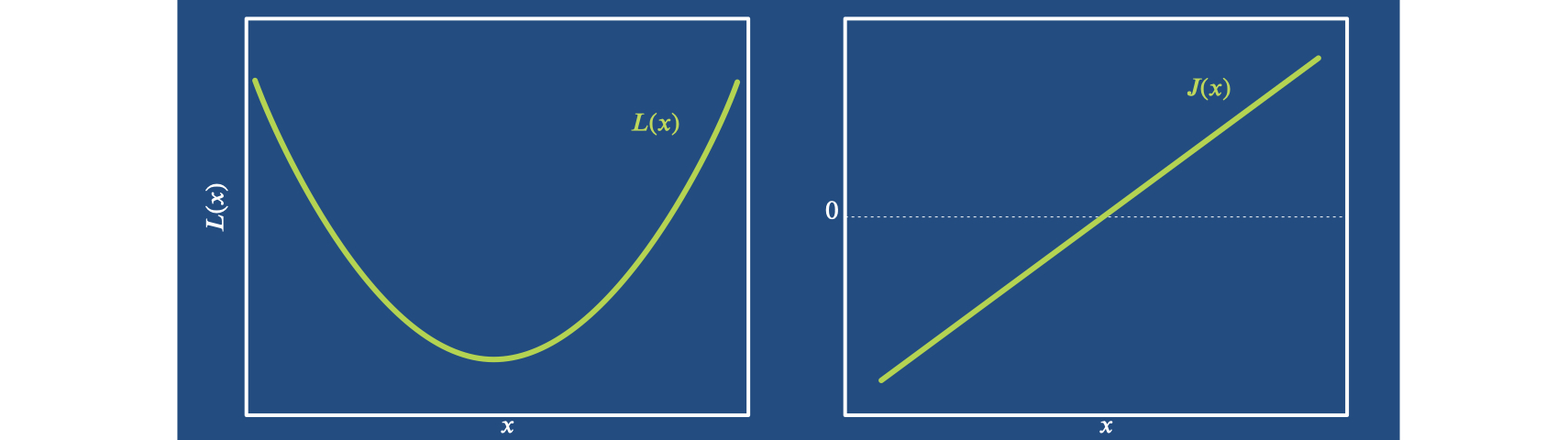
因此，我们可以用抛物线的形式 $\frac{1}{2}H(x-x^{\ast }{)}^2+c$ 来表示最佳值 $x^{\ast }$ 附近的 $L$ 。其中$c$表示常数偏移。在位置 $x$ 处，我们观察到 $H$ 和 $J^T=H\cdot (x_k-x^{\ast })$ 。将其重新排列后，可以直接得出计算最小值的方程：$x^{\ast }=x_k-\frac{J^T}{H}$。牛顿法默认以单步计算 $x^{\ast }$ ，因此牛顿法中的 $x$ 更新量给定为： $$\Delta =-\frac{J^T}{H}$$

让我们来看看牛顿法的收敛阶次。对于 $L$ 的最优值 $x^{\ast }$，让 ${\Delta }_n^{\ast }=x^{\ast }-x_n$ 表示从当前的 $x_n$ 到最优值的步长，如下图所示。

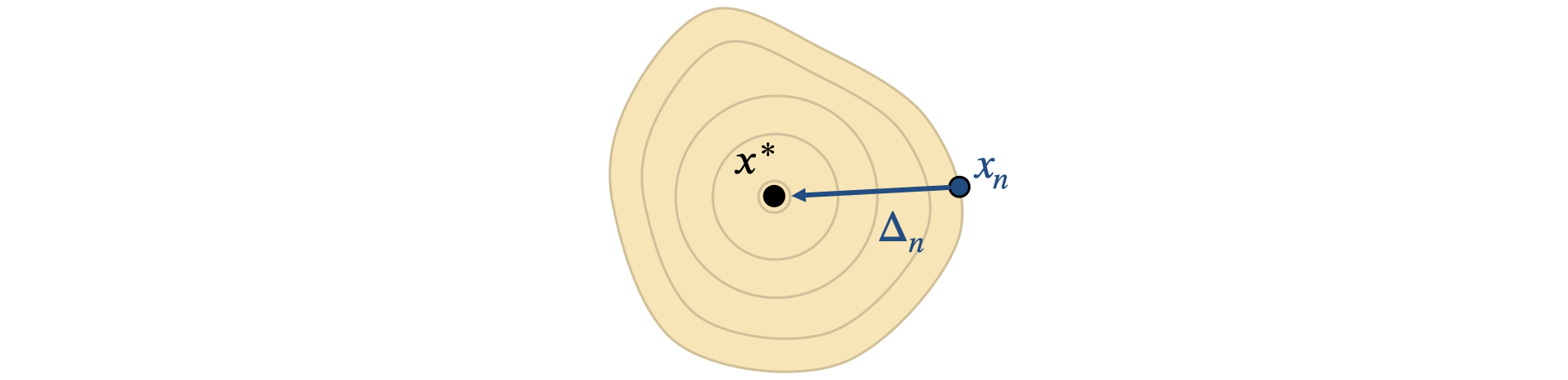
假设 $J$ 可微分，我们可以在 $x^{\ast }$ 处对 $J^T$ 进行拉格朗日展开：

$$\begin{array}{rl}0& =J^T(x^{\ast })=J^T(x_n)+H(x_n){\Delta }_n^{\ast }+\frac{1}{2}K({\xi }_n){{\Delta }_n^{\ast }}^2\\ \frac{J^T}{H}& =-\frac{K}{2H}{{\Delta }_n^{\ast }}^2-{\Delta }_n^{\ast }\end{array}$$

在第二行中，我们已经除以 $H$，并以缩短符号去掉了 $(x_n)$ 和 $({\xi }_n)$ 。当我们把这一行插入 ${\Delta }_n^{\ast }$ 时，我们会得到 $$\begin{array}{rl}{\Delta }_{n+1}^{\ast }& =x^{\ast }-x_{n+1}\\ & =x^{\ast }-(x_n-\frac{J^T}{H})\\ & ={\Delta }_n^{\ast }-\frac{K}{2H}{{\Delta }_n^{\ast }}^2-{\Delta }_n^{\ast }\\ & =-\frac{K}{2H}{{\Delta }_n^{\ast }}^2\end{array}$$

因此，与最优值的距离会因 ${{\Delta }_n^{\ast }}^2$ 的变化而改变，这意味着一旦我们足够接近最优值，就会出现二次收敛。这当然很好，但它仍然取决于前系数 $\frac{K}{2H}$，如果前系数 $>1$ 就会发散。请注意，这是一个精确的表达式，由于拉格朗日展开的缘故，没有截断。到目前为止，我们已经实现了二次收敛，但并不能保证收敛到最优。为此，我们必须允许步长可变。

2.8.4 自适应步长

因此，作为牛顿法的下一步，我们引入了步长可变的$\lambda$，从而得到迭代$x_{n+1}=x_n+\lambda \Delta =x_n-\lambda \frac{J^T}{H}$ 。如下图所示，如果 $L$ 不完全是抛物线，而且小的 $H$ 可能会以不理想的方式超调，那么这一点就特别有用。本例中最左侧的例子：

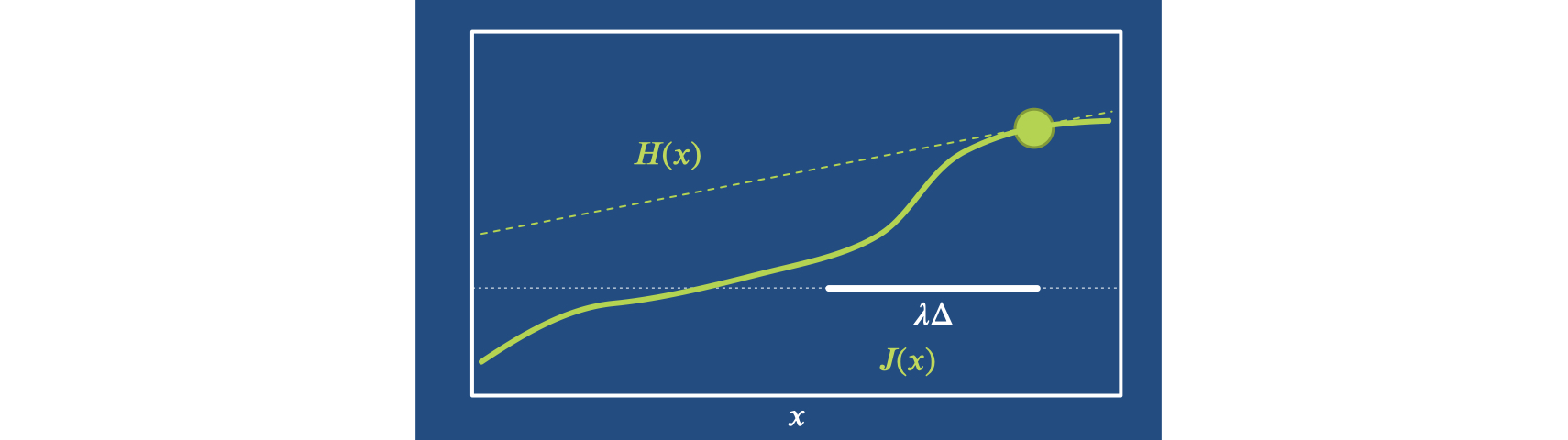
为了说明收敛性，我们需要一些基本假设：损失函数的凸性和平滑性。然后，我们将专注于证明损失会减少，并且我们会沿着一连串损失值较低的较小集合 $\forall xL(x)<L(x_n)$ 移动。

首先， 我们对 $L$ 应用基本定理：

$$L(x+\lambda \Delta )=L+{\int }_0^1\text{ds}J(x+s\lambda \Delta )\lambda \Delta ,$$

类似地， 使用它围绕此位置表达 $J$：

$$\begin{array}{r}J(x+s\lambda \Delta )=J+s\lambda {\Delta }^T{\int }_0^1\text{dt}H(x+st\lambda \Delta )\end{array}$$

将这个 $J^T$ 插入 $L$ 中会产生：

$$\begin{array}{rl}L(x+\lambda \Delta )-L(x)& ={\int }_0^1\text{d}s[J+s\lambda {\Delta }^T{\int }_0^1\text{d}tH(x+st\lambda \Delta ){]}^T\lambda \Delta \\ & ={\int }_0^1\text{d}s[-H\Delta +{\int }_0^1\text{d}tH(x+st\lambda \Delta )s\lambda \Delta {]}^T\lambda \Delta \\ & ={\int }_0^1\text{d}s{\int }_0^1\text{d}t[-H\Delta +H(x+st\lambda \Delta )s\lambda \Delta {]}^T\lambda \Delta \\ & ={\int }_0^1\text{d}s{\int }_0^1\text{d}t[-H\Delta (1+\lambda s)+[H(x+st\lambda \Delta )-H]s\lambda \Delta {]}^T\lambda \Delta \\ & =-(H\Delta {)}^T(1+\frac{\lambda }{2})\lambda \Delta +{\lambda }^2{\int }_0^1\text{d}ss{\int }_0^1\text{d}t[[H(x+st\lambda \Delta )-H]\Delta {]}^T\Delta \end{array}$$

在这里，我们首先使用了 $\Delta =-J^T/H$ ，然后把它移到第三行的积分中，与 $s\lambda \Delta$ 项一起。第四行将 $H\Delta$ 因数化。这样，我们就可以对上式（10）最后一行中的第一项 $-H\Delta (1+\lambda s)$ 进行积分。

在接下来的一系列步骤中，我们将首先使用 $(H\Delta {)}^T\Delta =\Vert H^{\frac{1}{2}}\Delta {\Vert }^2$。这一术语将简称为 $epsilon\equiv \Vert H^{\frac{1}{2}}\Delta {\Vert }^2$。由于 $H$ 的特性，这个 $epsilon$ "只是 "代表一个小的正因子，它会一直存在到最后。之后，在下面的第 3 行和第 4 行中，我们可以开始寻找损失变化的上限。我们首先使用考希-施瓦茨不等式，然后利用仿射共轭矩阵的特殊 Lipschitz 条件。对于 $H$，它的形式是 $\Vert H(x{)}^{-\frac{1}{2}}(H(y)-H(x))\Vert \le \mathcal{L}\Vert H(x{)}^{\frac{1}{2}}(y-x){\Vert }^2$。这就要求 $H$ 是对称的正定式，这在实际中并不是太不合理。承上启下，我们可以得到： $$\begin{array}{rl}\cdots & =-(\lambda +\frac{{\lambda }^2}{2})\cdot \Vert H^{\frac{1}{2}}\Delta {\Vert }^2+{\lambda }^2{\int }_0^1\text{d}ss{\int }_0^1\text{d}t[H(x+st\lambda \Delta )-H]\Delta {]}^T\Delta \\ & =-\lambda ϵ+\frac{{\lambda }^2ϵ}{2}+{\lambda }^2{\int }_0^1\text{d}ss{\int }_0^1\text{d}t[H^{-\frac{1}{2}}[H(x+st\lambda \Delta )-H]\Delta {]}^T{H}^{\frac{1}{2}}\Delta \\ & \le -\lambda ϵ+\frac{{\lambda }^2ϵ}{2}+{\lambda }^2{\int }_0^1\text{d}ss{\int }_0^1\text{d}t\Vert H^{-\frac{1}{2}}[H(x+st\lambda \Delta )-H]\Delta \Vert \cdot \Vert H^{\frac{1}{2}}\Delta \Vert \\ & \le -\lambda ϵ+\frac{{\lambda }^2ϵ}{2}+{\lambda }^3{\int }_0^1\text{d}s{s}^2{\int }_0^1\text{d}tt\mathcal{L}\Vert H^{\frac{1}{2}}\Delta {\Vert }^2\cdot \Vert H^{\frac{1}{2}}\Delta \Vert \\ & =-\lambda ϵ+\frac{{\lambda }^2ϵ}{2}+\mathcal{L}{\lambda }^3{\int }_0^1\text{d}s{s}^2{\int }_0^1\text{d}tt\Vert H^{\frac{1}{2}}\Delta {\Vert }^3\\ & =-\lambda ϵ+\frac{{\lambda }^2ϵ}{2}+\mathcal{L}{\lambda }^3{\int }_0^1\text{d}s{s}^2{\int }_0^1\text{d}tt{ϵ}^{\frac{3}{2}}\\ & =-\lambda ϵ+\frac{{\lambda }^2ϵ}{2}+\frac{{\lambda }^3\mathcal{L}{ϵ}^{\frac{3}{2}}}{6}\end{array}$$

由于 $H^T=H$，我们把 $H^{-\frac{1}{2}}$ 移到了第 2 行的积分内。在第 4 行中，除了应用特殊的 Lipschitz 条件外，我们尽可能地将 $s,t$ 和 $\lambda$ 从积分中移出。最后三行只是简化术语，用 $ϵ$ 表示 $H$ 的出现，并对积分进行评估。这样，我们就得到了以步长 $\lambda$ 为单位的三次方形式。最重要的是，第一个线性项是负的，因此对于较小的 $\lambda$ 将占主导地位。这样，我们就证明了对于足够小的 $\lambda$ 来说，步长将是负值： $$L(x+\lambda \Delta )=L(x)-\lambda ϵ+\frac{{\lambda }^2ϵ}{2}+\frac{{\lambda }^3\mathcal{L}{ϵ}^{\frac{3}{2}}}{6}$$

然而，这本质上要求我们自由选择 $\lambda$，因此该证明不适用于上述固定步长。它的一个很好的特性是，我们 "只 "要求 $H$ 的 Lipschitz 连续性，而不是 $J$ 或甚至 $L$。

总之，我们已经证明，牛顿方法的自适应步长可以收敛，这非常好。然而，它需要 Hessian $H$ 作为核心要素。不幸的是，$H$ 在实践中很难获得。这是一个真正的拦路虎，也是以下方法的动因。这些方法保留了牛顿法的基本步骤，但对 $H$ 进行了近似。

2.8.5 近似 Hessian

接下来， 我们将重新审视牛顿法导出的三种流行算法。

2.8.6 Broyden 方法

近似 $H$ 的第一种方法是做一个非常粗略的猜测，即从特征矩阵 $H_0=1$ 开始，然后通过有限差分近似迭代更新 $H_n$。对于布洛伊登方法，我们使用向量除法 $\frac{a}{b}\frac{a{b}^T}{b^{T}b}$。

为了简化有限差分，我们另外假设在当前位置 $x_n$ 时，已经达到 $J(x_n)=0$。当然，这并不一定正确，但在优化过程中，我们可以用下面这个简洁的表达式来修改 $H$：

$$H_{n+1}=H_n+\frac{J(x_{n+1}{)}^T}{\Delta }$$

和之前一样，我们对 $x$ 使用 $\Delta =-\frac{J^T}{H}$ 的步长，分母来自有限差分 $\frac{J(x_{n+1}{)}^T-J(x_n{)}^T}{\Delta }$，假设当前的雅各布值为零。请记住，这里的 $\Delta$ 是一个向量（见上文的向量分割），所以有限差分给出了一个大小为 $N\times N$ 的矩阵，可以添加到 $H_n$。

Broyden 方法的优势在于我们无需计算全Hessian，而且可以高效地评估$H$的更新。然而，上述两个假设使其成为一个非常粗糙的近似值，因此通过 $\frac{J^T}{H}$ 中的逆Hessian对更新步骤进行归一化也相应地不可靠。

2.8.7 BFGS

这就产生了 BFGS 算法（以_Broyden-Fletcher-Goldfarb-Shanno_命名），它引入了一些重要的改进：它不假定 $J$ 立即为零，并对更新的冗余部分进行补偿。这是必要的，因为有限差分 $(J(x_{n+1})-J(x_n))/{\Delta }_n$ 给出了 $H$ 的完整近似值。我们可以尝试执行某种平均程序，但这会严重破坏 $H_n$ 中的现有内容。因此，我们只沿着当前步长 $\Delta$ 减去 $H_n$ 中的现有条目。这样做是有道理的，因为有限差分近似正好可以得到沿 $\Delta$ 的估计值。结合使用向量分割 $\frac{a}{b}\frac{a{a}^T}{a^{T}b}$，这些变化给出了 $H$ 的更新步长： $$H_{n+1}=H_n+\frac{J(x_{n+1}{)}^T-J(x_n{)}^T}{{\Delta }_n}-\frac{H_n{\Delta }_n}{{\Delta }_n}$$

在实践中，BFGS 还利用直线搜索来确定步长 $\lambda$。由于 $H$ 的大小较大，通常使用的 BFGS 变体也会使用 $H$ 的缩小表示来节省内存。尽管如此，通过沿搜索方向的有限差分近似更新Hessian矩阵的核心步骤仍是 BFGS 的核心，并使其至少能部分补偿损失景观的缩放效应。目前，BFGS 变体是解决经典非线性优化问题最广泛使用的算法。

2.8.8 高斯牛顿法

通过限制 $L$ 为经典的 $L^2$ 损失，可以推导出牛顿法的另一个有吸引力的变体。这就是_高斯-牛顿（GN）算法。因此，我们仍然使用 $\Delta =-\frac{J^T}{H}$ ，但对于任意的 $f(x)$，则依赖于 $L=|f{|}^2$ 形式的平方损失。$f$的导数用$J_f,H_f$表示，而不是像之前那样用$J,H$表示$L$。由于链式规则，我们有 $J=2f^T{J}_f$。

二阶导数得出以下表达式。为了简化 GN，我们省略了下面第二行中的二阶项： $$\begin{array}{rl}H& =2J_f^T{J}_f+2f^T{H}_f\\ & \approx 2J_f^T{J}_f\\ & =2\frac{J^{T}J}{4|f{|}^2}\\ & =\frac{J^{T}J}{2L}\end{array}\text{\hspace{1em}(13)}$$

在这里，一阶近似的剩余 $J_f^T{J}_f$ 项可以简化，这要归功于我们对 $L^2$ 损失的关注：$J_f=J/(2f^T)$ 和 $|f{|}^2=L$。

等式 (13) 的最后一行意味着我们基本上是用 $J$ 的平方来逼近 Hessian。这在很多情况下都是合理的，将其插入到我们上面的更新步骤中，就得到了高斯-牛顿更新 ${\Delta }_{\text{GN}}\approx -\frac{J^T}{J^{T}J}$。

看这个更新， 它本质上采用了形式 ${\Delta }_{\text{GN}}\approx -\frac{1}{J}$ 的步骤， 即更新基于 $L$ 的雅可比的逼近逆。这为所有参数提供了大致相等的步长， 作为这样的提供了我们将在本书后面重新审视的有趣构建块。以上形式意味着我们仍然必须求一个大矩阵的逆， 这代价高昂， 且矩阵本身可能甚至不可逆。

2.8.9 回到深度学习

上文我们已经说明，牛顿方法是许多流行的非线性优化算法的核心。现在，高斯-牛顿法终于为我们提供了通向深度学习算法的阶梯，特别是通向亚当优化器的阶梯。

2.8.10 Adam

像往常一样，我们从牛顿步骤 $\Delta =-\lambda \frac{J^T}{H}$ 开始，但即使是高斯-牛顿对 $H\approx J^{T}J$ 的最简单近似，也需要求一个潜在的巨大矩阵的逆。这对于神经网络的权重来说是不可行的，因此一个合理的问题是，我们如何进一步简化这一步骤？对于Adam来说，答案就是：用对角线近似。具体来说，Adam使用： $$H\approx \sqrt{\text{diag}(J^{T}J)}$$

这只是真正的Hessian的一个非常粗略的近似值。我们在这里使用的只是平方一阶导数，当然，一般来说，${\left(\frac{\partial f}{\partial x}\right)}^2\ne \frac{{\partial }^{2}f}{\partial x^2}.$。这只适用于高斯-牛顿的一阶近似，即方程 (13) 的第一项。现在，亚当更进一步，只保留 $J^{T}J$ 的对角线。这个量在深度学习中以权重梯度的形式随时可用，并使 $H$ 的反演变得微不足道。因此，它至少提供了对单个权重曲率的一些估计，但忽略了它们之间的相关性。

有趣的是，亚当并没有通过 $\text{diag}(J^{T}J)$ 进行完全反转，而是使用了分量平方根。这就有效地得到了 $\sqrt{\text{diag}(J^{T}J)}\approx \sqrt{\text{diag}(J^2)}\approx \text{diag}(J)$。因此，亚当沿着 $\Delta \approx \text{sign}(-J)$ 移动，近似于在所有维度上执行一个固定大小的步长。

在实践中，Adam还引入了一些技巧，即计算梯度 $J^T$ 以及梯度平方动量，在优化迭代过程中平均这两个量。这使得估算结果更加稳健，这一点至关重要：如果梯度输入错误地过小，那么归一化可能会导致爆炸。Adam 还在除法时增加了一个小常数，而平方根同样有助于减轻超调。

总而言之：Adam 利用一阶更新和对角高斯-牛顿近似赫塞斯进行归一化。此外，它还利用动量进行稳定。

2.8.11 梯度下降

为了实现梯度下降（GD）优化，我们现在采取最后一步，在 $-\lambda \frac{J^T}{H}$ 中假设 $H=1$。这样，我们就有了一个由缩放梯度 $\Delta =-\lambda J^T$ 组成的更新。

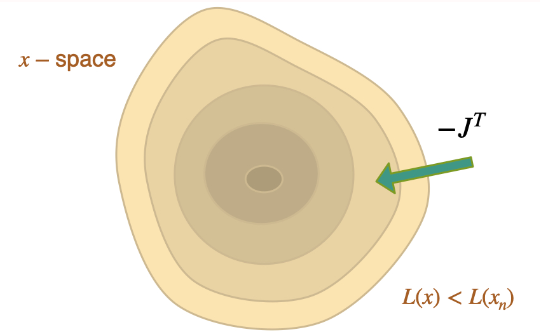
有趣的是，在没有任何形式的反转的情况下，$J^T$ 本身具有添加到 $x$ 的正确形状，但它 "生活 "在错误的空间 $1/x$ 中，而不是 $x$ 本身。上述所有 "经典 "方案以某种形式使用的 $J^{-1}$ 与 $J^T$ 本质上是不同的，这一事实就说明了这一点。缺乏反演步骤的问题在涉及物理学的问题中尤为突出，因此也是本章的重要启示之一。我们将在以后的 Scale-Invariance and Inversion中更详细地讨论这个问题。现在，我们建议大家牢记不同算法之间的关系，即使 "仅仅 "使用 Adam 或 GD。

最后，让我们来看看 GD 的收敛性。我们再次假设 $L$ 具有凸性和可微性。用泰勒级数展开 $\Delta$ 的一步，用 Lipschitz 条件$J(x+\Delta )-J(x)\le \mathcal{L}\Delta$限定二阶项，我们得到

$$\begin{array}{rl}L(x+\Delta )-L(x)& \le J(x)\Delta +\frac{\mathcal{L}}{2}|\Delta {|}^2\\ & =J(-\lambda J^T)+\frac{\mathcal{L}}{2}|-\lambda J^T{|}^2\\ & =-\lambda J{J}^T+{\lambda }^2\frac{\mathcal{L}}{2}|J{|}^2\\ & =-\lambda |J{|}^2+{\lambda }^2\frac{\mathcal{L}}{2}|J{|}^2\end{array}$$

就像上面方程(11)中的牛顿方法一样，我们有一个负线性项，它在足够小的$\lambda$时支配着损失。结合起来，由于第一行中的 Lipschitz 条件，我们可以得到以下上界 $L(x+\Delta )\le L(x)-\lambda |J{|}^2+\frac{{\lambda }^2\mathcal{L}}{2}.|J{|}^2$.通过选择 $\lambda \le \frac{1}{\mathcal{L}}$，我们可以进一步简化这些项，并得到一个取决于 $J$ 平方的上界：$L(x+\Delta )\le L(x)-\frac{\lambda }{2}.|J{|}^2$，从而确保收敛。

遗憾的是，这一结果在实践中对我们帮助不大，因为在深度学习中，梯度的所有常见用法 $\mathcal{L}$ 都是未知的。不过，我们还是应该知道，梯度的 Lipschitz 常数在理论上可以为 GD 提供收敛保证。

至此，我们结束了经典优化器及其与深度学习方法的关系之旅。值得注意的是，为了清楚起见，我们在这里重点讨论了非随机算法，因为随机算法的证明会变得更加复杂。

有了这些背景知识，现在正是开始研究一些实际例子的好时机，这些例子从尽可能简单的开始，采用完全有监督的方法进行训练。