逆问题包含了科学中的大量实际应用。一般来说，这里的目标不是直接计算一个物理场，如未来某个时间的速度（这是正解的典型情况），而是更通用地计算模型方程中的一个或多个参数，从而满足某些约束条件。一个非常常见的目标是在某些约束条件下找到单个参数的最优设置。例如，这可能是一个平流扩散模型的全局扩散常数，使其尽可能精确地符合测量数据。通过观测或重建初始条件（如粒子成像测速）来调整任何模型参数，都会遇到逆问题。更复杂的情况旨在计算最佳条件下的边界几何形状，例如在流体流动中获得阻力最小的形状。

下面的一个关键方面是，我们的目标并不只是求解一个逆问题的_单个实例，而是希望使用深度学习来解决更多的逆问题。因此，与{doc}physicalloss-code或{doc}diffphys-code-ns的可微分物理（DP）优化不同，我们已经解决了逆问题特定实例的优化问题，而我们现在的目标是训练一个学习求解更大类逆问题（即整个求解流形）的 NN。不过，我们当然需要依赖这些问题在一定程度上的相似性，否则就没有什么可学的了（解流形中隐含的连续性假设也就不成立了）。

下面我们将运行一个极具挑战性的测试案例，作为这些逆问题的代表：我们的目标是计算一个高维控制函数，在不可压缩流体模拟的整个过程中施加力，以达到流体中被动迁移标记的预期目标状态。这意味着我们只有非常间接的约束条件需要满足（序列结束时的单一状态）和大量自由度（控制力函数是一个时空函数，其自由度与流场本身相同）。

控制的长期性是这是一个棘手的逆问题的原因之一：物理系统状态的任何变化都可能导致后期的巨大变化，因此控制器需要预测系统在受到影响时的行为。这意味着网络还需要学习底层物理是如何演变和变化的，而这正是 DP 训练中的梯度发挥作用的地方，它可以引导学习任务朝着能够实现目标解的方向前进。

run in colab

13.1 描述

使用overview-equations 中的符号，可以得到最小化问题

$arg min_{θ} m \sum i \sum (f (x_{m, i}; θ) - y_{m, i}^{*})^{2},$

其中， $y_{m, i}^{*}$ 表示标记场目标状态的样本， $x_{m, i}$ 表示标记密度的模拟状态。与之前一样，索引 $i$ 表示在不同空间位置（通常是所有网格单元）对我们的解进行采样，而索引 $m$ 则表示大量不同目标状态的集合。

我们的目标是训练两个权重分别为 $θ_{OP}$ 和 $θ_{CFE}$ 的网络，从而使序列： $u_{n}, d_{n} = P (CFE (P (CFE (\dots P (CFE (u_{0}, d_{0}, d_{OP})) \dots)))) = (P CFE)^{n} (u_{0}, d_{0}, d_{OP}) .$

使上述损失最小。 $OP$ 网络是一个预测器，它确定了 $CFE$ 的行动应该瞄准的状态 $d_{OP}$ ，也就是说，其进行长期规划并据此确定了操作。给定目标 $d^{*}$ ,它计算 $d_{OP} = OP (d, d^{*}) = f_{OP} (d, d^{*}; θ_{OP})$ 。 $CFE$ 通过计算 $u + f_{CFE} (u, d, f_{OP} (d, d^{*}; θ_{OP}); θ_{CFE})$ 以可加方式作用于速度场,其中我们使用 $f_{OP}$ 和 $f_{CFE}$ 分别表示 $OP$ 和 $CFE$ 的神经网络表示,使用 $d^{*}$ 表示目标密度状态。 $θ_{OP}$ 和 $θ_{CFE}$ 表示相应的网络权重。

对于这个问题，模型偏微分方程 $P$ 包含速度为 $u$ 的二维不可压缩纳维-斯托克斯方程的离散化版本：

$\frac{\partial u _{x}}{\partial t} + u \cdot \nabla u_{x} \frac{\partial u _{y}}{\partial t} + u \cdot \nabla u_{y} s.t. \nabla \cdot u = - \frac{1}{ρ} \nabla p = - \frac{1}{ρ} \nabla p = 0,$

没有显式粘度，标记密度 $d$ 的额外传输方程为 $\frac{\partial d}{\partial t} + u \cdot \nabla d = 0$ 。

总结一下, 我们有一个预测器 $OP$ ，其给出一个方向，一个行为体 $CFE$ 对物理模型 $P$ 施加力。它们都需要配合才能在 $n$ 次模拟迭代后达到给定的目标。从这个公式可以看出, 这并不是一个简单的逆问题，尤其是因为所有三个函数都是非线性的。这正是 DP 方法的梯度如此重要的原因。(上述观点还表明强化学习是一种潜在的选择。在{doc} reinflearn-code 中，我们将比较 DP 与这些替代方法。)

13.2 不可压缩流体的控制

接下来的章节将引导您使用 Φ_Flow完成从数据生成到网络训练的所有必要步骤。由于控制问题的复杂性，我们将先对网络进行有监督的初始化，然后再使用 DP 进行更精确的端到端训练。（注意：本例使用的是Φ_Flow的旧版本 1.4.1）

下面的代码复制了Learning to Control PDEs with Differentiable Physics{cite}"holl2019pdecontrol "中的一个反问题示例（形状转换实验），更多细节可参见论文附录的 D.2 节。

首先，我们需要加载 phiflow 并查看 PDE-Control的 git 仓库，其中还包含一些带有初始形状的 numpy 数组。

!pip install --quiet phiflow==1.4.1

import matplotlib.pyplot as plt
from phi.flow import *

if not os.path.isdir('PDE-Control'):
  print("Cloning, PDE-Control repo, this can take a moment")
  os.system("git clone --recursive https://github.com/holl-/PDE-Control.git")
    
# now we can load the necessary phiflow libraries and helper functions
import sys; sys.path.append('PDE-Control/src')
from shape_utils import load_shapes, distribute_random_shape
from control.pde.incompressible_flow import IncompressibleFluidPDE
from control.control_training import ControlTraining
from control.sequences import StaggeredSequence, RefinedSequence

13.3 数据生成

在开始训练之前，我们必须生成一个训练数据集，即一组真值时间序列 $u^{*}$ 。由于下面的训练非常复杂，我们将采用一种分阶段的方法，先预先训练一个有监督的网络作为粗略的初始化，然后再对其进行改进，使其能够学习控制，并将目光越放越远。(这将通过训练处理越来越长序列的专门网络来实现）。

首先，让我们设置一个域和数据生成步骤的基本参数。

domain = Domain([64, 64])  # 1D Grid resolution and physical size
step_count = 16  # how many solver steps to perform
dt = 1.0  # Time increment per solver step
example_count = 1000
batch_size = 100
data_path = 'shape-transitions'
pretrain_data_path = 'moving-squares'
shape_library = load_shapes('PDE-Control/notebooks/shapes')

最后一行中的 shape_library 包含十种不同的形状，我们将使用它们在随机位置初始化标记密度。

这就是这些形状的样子：

import pylab
pylab.subplots(1, len(shape_library), figsize=(17, 5))
for t in range(len(shape_library)):
    pylab.subplot(1, len(shape_library), t+1)
    pylab.imshow(shape_library[t], origin='lower')

下面的单元格使用这些形状来创建我们要训练网络的数据集。每个示例都由起始帧和目标帧（结束帧）组成，起始帧和目标帧是通过在域内某处放置shape_library中的随机形状生成的。

for scene in Scene.list(data_path): scene.remove()

for _ in range(example_count // batch_size):
    scene = Scene.create(data_path, count=batch_size, copy_calling_script=False)
    print(scene)
    start = distribute_random_shape(domain.resolution, batch_size, shape_library)
    end__ = distribute_random_shape(domain.resolution, batch_size, shape_library)
    [scene.write_sim_frame([start], ['density'], frame=f) for f in range(step_count)]
    scene.write_sim_frame([end__], ['density'], frame=step_count)

shape-transitions/sim_000000
shape-transitions/sim_000100
shape-transitions/sim_000200
shape-transitions/sim_000300
shape-transitions/sim_000400
shape-transitions/sim_000500
shape-transitions/sim_000600
shape-transitions/sim_000700
shape-transitions/sim_000800
shape-transitions/sim_000900

由于该数据集不包含任何中间帧，因此无法进行监督预训练。这是因为预训练 CFE 网络需要两个连续帧，而预训练 $OP_{n}$ 网络则需要三个距离为 $n /2$ 的帧。

相反，我们创建了包含这些中间帧的第二个数据集。这个数据集不需要与实际数据集非常接近，因为它只用于通过预训练进行网络初始化。在这里，我们围绕域线性移动一个矩形。

for scene in Scene.list(pretrain_data_path): scene.remove()

for scene_index in range(example_count // batch_size):
    scene = Scene.create(pretrain_data_path, count=batch_size, copy_calling_script=False)
    print(scene)
    pos0 = np.random.randint(10, 56, (batch_size, 2))  # start position
    pose = np.random.randint(10, 56, (batch_size, 2))  # end position
    size = np.random.randint(6,  10,  (batch_size, 2))
    for frame in range(step_count+1):
        time = frame / float(step_count + 1)
        pos = np.round(pos0 * (1 - time) + pose * time).astype(np.int)
        density = AABox(lower=pos-size//2, upper=pos-size//2+size).value_at(domain.center_points())
        scene.write_sim_frame([density], ['density'], frame=frame)

moving-squares/sim_000000
moving-squares/sim_000100
moving-squares/sim_000200
moving-squares/sim_000300
moving-squares/sim_000400
moving-squares/sim_000500
moving-squares/sim_000600
moving-squares/sim_000700
moving-squares/sim_000800
moving-squares/sim_000900

13.4 监督初始化

首先，我们将 1000 个数据样本分成 100 个测试样本、100 个验证样本和 800 个训练样本。

test_range = range(100)
val_range = range(100, 200)
train_range = range(200, 1000)

下面的单元训练所有 $OP_{n} \forall n \in {2, 4, 8, 16}$ .这里的 $n$ 表示网络预测目标的时间步数。为了覆盖更长的时间跨度，我们在这里使用系数 2 来分层划分物理系统应受控制的时间间隔。

ControlTraining 类用于设置相应的优化问题。监督初始化的损失定义为中心帧处的速度观测损失:

$L_{o}^{sup} = OP (d_{t_{i}}, d_{t_{j}}) - d_{(t_{i} + t_{j}) /2}^{*}^{2} .$

因此，不需要模拟序列（sequence_class=None），只需要在帧 $\frac{n}{2}$ 处进行观测损失（obs_loss_frames=[n // 2]）。预训练的网络检查点存储在 supervised_checkpoints 中。

注：下一个单元将运行一段时间。PDE-Control git 仓库附带了一组预训练网络。因此，如果您想专注于评估，可以跳过训练，直接加载预训练网络，方法是注释掉训练单元格，并取消注释加载下面的单元格。

supervised_checkpoints = {}

for n in [2, 4, 8, 16]:
    app = ControlTraining(n, IncompressibleFluidPDE(domain, dt),
                          datapath=pretrain_data_path, val_range=val_range, train_range=train_range, trace_to_channel=lambda _: 'density',
                          obs_loss_frames=[n//2], trainable_networks=['OP%d' % n],
                          sequence_class=None).prepare()
    for i in range(1000):
        app.progress()  # Run Optimization for one batch
    supervised_checkpoints['OP%d' % n] = app.save_model()

supervised_checkpoints # this is where the checkpoints end up when re-training:

{'OP16': '/root/phi/model/control-training/sim_000003/checkpoint_00001000',
 'OP2': '/root/phi/model/control-training/sim_000000/checkpoint_00001000',
 'OP4': '/root/phi/model/control-training/sim_000001/checkpoint_00001000',
 'OP8': '/root/phi/model/control-training/sim_000002/checkpoint_00001000'}

# supervised_checkpoints = {'OP%d' % n: 'PDE-Control/networks/shapes/supervised/OP%d_1000' % n for n in [2, 4, 8, 16]}

至此，OP 网络的预训练结束。通过这些网络，我们至少可以对运动进行粗略规划，并在接下来的端到端训练中加以完善。不过，在此之前，我们将对 $CFE$ 网络进行初始化，这样我们就可以执行操作，即对模拟施加力。这与 $OP$ 网络是完全分离的。

13.5 使用可微分物理的 CFE 预训练

为了对 $CFE$ 网络进行预训练，我们使用可微分求解器进行了一次模拟。

下面的单元格将从头开始训练 $CFE$ 网络。如果你手头有一个预训练的网络，可以跳过训练，通过运行之后的单元来加载检查点。

app = ControlTraining(1, IncompressibleFluidPDE(domain, dt),
                      datapath=pretrain_data_path, val_range=val_range, train_range=train_range, trace_to_channel=lambda _: 'density',
                      obs_loss_frames=[1], trainable_networks=['CFE']).prepare()
for i in range(1000):
    app.progress()  # Run Optimization for one batch
supervised_checkpoints['CFE'] = app.save_model()

# supervised_checkpoints['CFE'] = 'PDE-Control/networks/shapes/CFE/CFE_2000'

请注意，由于 $CFE$ 网络只推断状态对之间的作用力，因此我们实际上并没有设置模拟训练。

# [TODO, show preview of CFE only?]

13.6 使用可微分物理的端到端训练

现在，两种网络类型的第一个版本都已存在，我们可以启动当前设置中最重要的步骤：通过可微分流体求解器对两种网络进行端到端耦合训练。虽然预训练阶段依赖于监督训练，但下一步将显著提高控制质量。

为了在 phiflow 中使用可微分物理损失对 $CFE$ 和所有 $OP_{n}$ 网络进行端到端训练，我们使用交错执行方案创建了一个新的 ControlTraining"实例。

下面的单元格在不初始化网络权重的情况下，用 step_count 求解器步骤构建计算图。

staggered_app = ControlTraining(step_count, IncompressibleFluidPDE(domain, dt),
                                datapath=data_path, val_range=val_range, train_range=train_range, trace_to_channel=lambda _: 'density',
                                obs_loss_frames=[step_count], trainable_networks=['CFE', 'OP2', 'OP4', 'OP8', 'OP16'],
                                sequence_class=StaggeredSequence, learning_rate=5e-4).prepare()

App created. Scene directory is /root/phi/model/control-training/sim_000005 (INFO), 2021-04-09 00:41:17,299n

Sequence class: <class 'control.sequences.StaggeredSequence'> (INFO), 2021-04-09 00:41:17,305n

Partition length 16 sequence (from 0 to 16) at frame 8
Partition length 8 sequence (from 0 to 8) at frame 4
Partition length 4 sequence (from 0 to 4) at frame 2
Partition length 2 sequence (from 0 to 2) at frame 1
Execute -> 1
Execute -> 2
Partition length 2 sequence (from 2 to 4) at frame 3
Execute -> 3
Execute -> 4
Partition length 4 sequence (from 4 to 8) at frame 6
Partition length 2 sequence (from 4 to 6) at frame 5
Execute -> 5
Execute -> 6
Partition length 2 sequence (from 6 to 8) at frame 7
Execute -> 7
Execute -> 8
Partition length 8 sequence (from 8 to 16) at frame 12
Partition length 4 sequence (from 8 to 12) at frame 10
Partition length 2 sequence (from 8 to 10) at frame 9
Execute -> 9
Execute -> 10
Partition length 2 sequence (from 10 to 12) at frame 11
Execute -> 11
Execute -> 12
Partition length 4 sequence (from 12 to 16) at frame 14
Partition length 2 sequence (from 12 to 14) at frame 13
Execute -> 13
Execute -> 14
Partition length 2 sequence (from 14 to 16) at frame 15
Execute -> 15
Execute -> 16
Target loss: Tensor("truediv_16:0", shape=(), dtype=float32) (INFO), 2021-04-09 00:41:44,654n

Force loss: Tensor("truediv_107:0", shape=(), dtype=float32) (INFO), 2021-04-09 00:41:51,312n

Supervised loss at frame 16: Tensor("truediv_108:0", shape=(), dtype=float32) (INFO), 2021-04-09 00:41:51,332n

Setting up loss (INFO), 2021-04-09 00:41:51,338n

Preparing data (INFO), 2021-04-09 00:42:32,417n

Initializing variables (INFO), 2021-04-09 00:42:32,443n

Model variables contain 0 total parameters. (INFO), 2021-04-09 00:42:36,418n

Validation (000000): Learning_Rate: 0.0005, GT_obs_16: 399498.75, Loss_reg_unscaled: 1.2424506, Loss_reg_scale: 1.0, Loss: 798997.5 (INFO), 2021-04-09 00:42:59,618n

接下来的单元格使用监督检查点初始化网络, 然后联合训练所有网络。您可以增加优化步骤的数量或多次执行下一个单元格以进一步提高性能。

注意: 下一单元格需要运行一段时间。或者, 您可以跳过此单元格, 改为使用下面单元格中的代码加载预训练网络。

staggered_app.load_checkpoints(supervised_checkpoints)
for i in range(1000):
    staggered_app.progress()  # run staggered Optimization for one batch
staggered_checkpoint = staggered_app.save_model()

# staggered_checkpoint = {net: 'PDE-Control/networks/shapes/staggered/all_53750' for net in ['CFE', 'OP2', 'OP4', 'OP8', 'OP16']}
# staggered_app.load_checkpoints(staggered_checkpoint)

既然网络已经训练好了，我们就可以从测试集中推断出一些轨迹。(这与原论文中的图 5b 和 18b 相对应）

下面的单元格选取了前 100 个配置，即 "test_range "定义的测试集，并让网络推断出相应逆问题的解。

states = staggered_app.infer_all_frames(test_range)

通过下面的索引列表 "批次"，您可以选择显示部分解决方案。每一行显示的都是一个时间序列，从初始条件开始，在 16 个时间步长内使用 NN 控制力进行模拟演化。最后一步，即 $t = 16$ 应该与最右边图片中显示的目标一致。

batches = [0,1,2]

pylab.subplots(len(batches), 10, sharey='row', sharex='col', figsize=(14, 6))
pylab.tight_layout(w_pad=0)

# solutions
for i, batch in enumerate(batches):
    for t in range(9):
        pylab.subplot(len(batches), 10, t + 1 + i * 10)
        pylab.title('t=%d' % (t * 2))
        pylab.imshow(states[t * 2].density.data[batch, ..., 0], origin='lower')

# add targets
testset = BatchReader(Dataset.load(staggered_app.data_path,test_range), staggered_app._channel_struct)[test_range]
for i, batch in enumerate(batches):
        pylab.subplot(len(batches), 10, i * 10 + 10)
        pylab.title('target')
        pylab.imshow(testset[1][i,...,0], origin='lower')

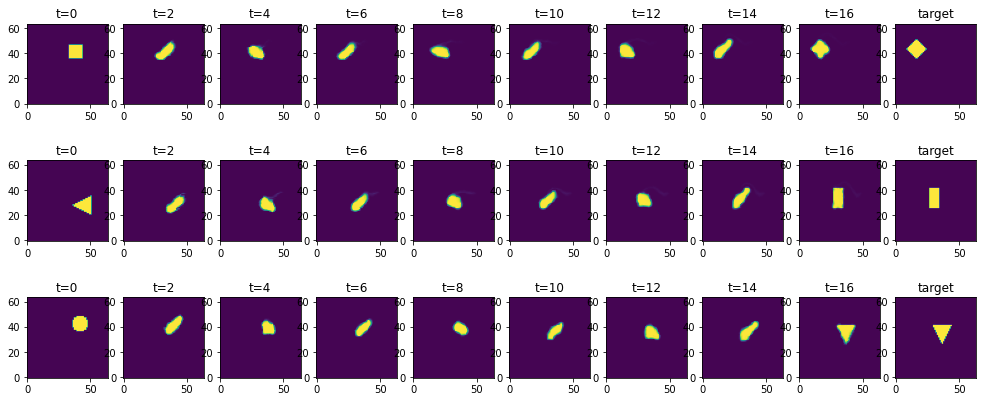
正如您在最右边的两列中看到的，该网络在求解这些逆问题方面做得非常出色：流体标记被推到正确的位置，并以正确的方式变形以匹配目标。

对神经网络来说，这里看起来相当简单的事情实际上是一项棘手的任务：它需要在 16 个时间积分步长内指导完整的二维纳维-斯托克斯模拟。因此，如果施加的力稍有偏差或不连贯，流体就会开始混乱地旋转和运动。不过，网络已经学会了保持运动的一致性，并引导标记密度到达目标位置。

接下来，我们通过比较最终密度配置相对于初始密度的平均绝对误差来量化误差率。按照上述标准训练设置，下一个单元的相对残余误差应为 5-6%。反之亦然，这意味着约 94% 以上的标记密度最终会出现在正确的位置上！

errors = []
for batch in enumerate(test_range):
  initial = np.mean( np.abs( states[0].density.data[batch, ..., 0] - testset[1][batch,...,0] )) 
  solution = np.mean( np.abs( states[16].density.data[batch, ..., 0] - testset[1][batch,...,0] )) 
  errors.append( solution/initial )
print("Relative MAE: "+format(np.mean(errors)))

Relative MAE: 0.05450168251991272

13.7 下一步

要对此源代码进行进一步实验, 您可以例如:

更改 test_range 索引以查看不同的示例, 或使用新的形状作为目标来测试训练控制器网络的概括能力。
尝试使用 RefinedSequence (而不是 StaggeredSequence)与预测细化方案一起进行训练。这将进一步改善控制并减少密度误差。