让我们从一个非常简化的例子开始，突出物理学习方法的一些关键能力。假设我们的物理模型是一个非常简单的方程：沿着正x轴的抛物线。

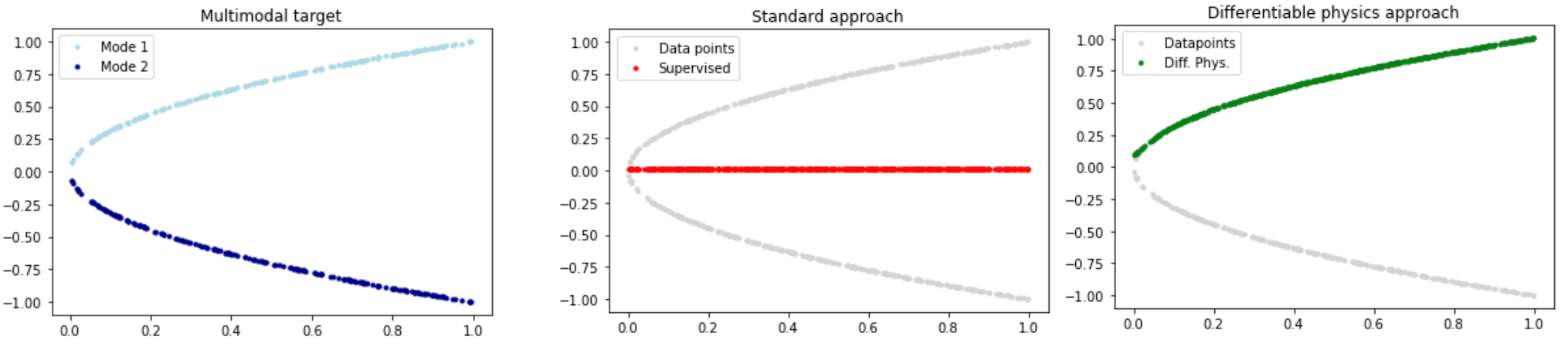
虽然非常简单，但每个x点都有两个解，即我们有两种模式，一个在x轴上方，另一个在下方，如下图左侧所示。如果我们不注意，传统的学习方法会给出一个完全错误的近似解，如下面中间图中红色线所示。通过改进学习设置，理想情况下通过使用离散化的数值求解器，我们至少可以准确表示解的一种模式（如右侧绿色线所示）。

图1：有监督的物理训练与有区别的物理训练

1.1 可微物理学

下面章节的一个关键概念我们将其称之为可微物理学(Differentiable Physics，DP)。这意味着我们可以使用模型方程的领域知识，然后将这些模型的离散化版本整合到训练过程中。正如其名称所暗示的那样，具有可微的表达式对于支持神经网络的训练至关重要。

让我们通过以下示例来说明利用可微分物理进行深度学习的性质：我们希望找到一个未知函数 $f^{*}$ ，其接受来自 $X$ 的输入，并在空间 $Y$ 中生成解，即 $f^{*} : X \to Y$ 。在接下来的内容中，我们经常用 $*$ 上标表示理想化的、未知的函数，其与没有这个上标的离散化、可实现的函数相对应。

另外假设我们有一个通用的微分方程 $P^{*} : Y \to Z$ （我们的“模型”方程），它编码了解的某种属性，例如我们希望匹配的某种真实世界的行为。接下来， $P^{*}$ 通常代表时间演化，但它也可以是质量守恒的约束条件（那么 $P^{*}$ 将衡量散度）。但为了尽可能保持简单，在接下来的内容中，我们将关注一个将解映射回输入空间 $X$ 的模型，即 $P^{*} : Y \to X$ 。

通过使用神经网络 $f$ 来学习未知的理想函数 $f^{*}$ ，我们可以采用经典的“监督式”训练方法来通过收集数据获取 $f$ 。这种经典的设置需要通过从 $X$ 中采样 $x$ ，并添加相应的解 $y$ 来获得数据集。我们可以通过经典的数值技术来获取这些数据。然后，我们按照通常的方式利用这个数据集来训练神经网络。

与这种监督方法相比，采用可微分物理方法利用了一个事实：即我们通常可以使用物理模型 $P$ 的离散化版本，并将其用于指导 $f$ 的训练。也就是说，我们希望 $f$ 知道我们的模拟器 $P$ ，并与其进行交互。这可以极大地改善学习效果，正如我们将在下面通过一个非常简单的例子进行说明的那样（更复杂的例子将在后面介绍）。

需要注意的是，为了使可微分物理方法起作用，正如其名称所暗示的那样， $P$ 必须是可微分的。这些微分以梯度的形式出现，是推动学习过程的关键。

1.2 寻找抛物线的反函数

为了说明监督和可微分物理方法的区别，我们考虑以下简化的场景：给定函数 $P : y \to y^{2}$ ，其中 $y$ 在区间 $[0, 1]$ 内，需要找到未知函数 $f$ ，使得对于所有 $[0, 1]$ 内的 $x$ ，都满足 $P (f (x)) = x$ 。注意：为了使事情更有趣，我们在这里使用 $y^{2}$ 来表示 $P$ ，而不是更常见的抛物线 $x^{2}$ ，并且对于这个简单的情况，“离散化”只需要通过在计算机中用浮点数表示 $x$ 和 $y$ 来实现。

我们知道， $f$ 的解可以是正或负的平方根函数（它们的分段组合也是可能的）。知道这并不是太困难，一个可行的解决方案是训练一个神经网络来近似这个逆映射 $f$ 。以经典有监督的方式（即纯粹基于数据）来实现这一点，显然是一个不错的起点，毕竟该方法已被证明是其他各种应用（如计算机视觉）的有力工具。

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt

对于监督训练，我们可以使用求解器 $P$ 来预先计算训练所需的解：随机选择正或负平方根中的其中一个。这类似于一般情况，我们会收集所有可用的数据（例如使用优化技术来计算求解）。这种数据收集通常不会偏向于多模式解中的某个特定模式。

# X-Data
N = 200
X = np.random.random(N)
# Generation Y-Data
sign = (- np.ones((N,)))**np.random.randint(2,size=N)
Y = np.sqrt(X) * sign

利用代码显示图形：

plt.scatter(X,Y,s=9,color='red')

此时生成的点如图所示。

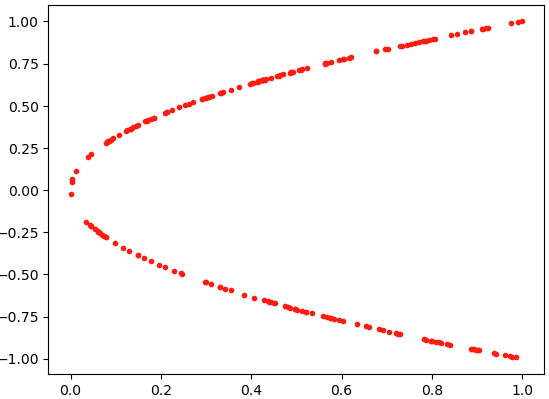
现在我们将使用一个简单的keras架构定义一个网络、损失函数和训练配置，该网络使用ReLU激活函数。

# Neural network
act = tf.keras.layers.ReLU()
nn_sv = tf.keras.models.Sequential([
tf.keras.layers.Dense(10, activation=act, input_shape=(1,)),
tf.keras.layers.Dense(10, activation=act),
tf.keras.layers.Dense(1,activation='linear')])

我们可以通过一个简单的均方误差损失函数开始训练，使用Keras的fit函数进行训练：

# Loss function
loss_sv = tf.keras.losses.MeanSquaredError()
optimizer_sv = tf.keras.optimizers.Adam(learning_rate=0.001)
nn_sv.compile(optimizer=optimizer_sv, loss=loss_sv)
# Training
results_sv = nn_sv.fit(X, Y, epochs=5, batch_size= 5, verbose=1)

训练过程如下所示。

Epoch 1/5
40/40 [==============================] - 0s 1ms/step - loss: 0.5084
Epoch 2/5
40/40 [==============================] - 0s 1ms/step - loss: 0.5022
Epoch 3/5
40/40 [==============================] - 0s 1ms/step - loss: 0.5011
Epoch 4/5
40/40 [==============================] - 0s 1ms/step - loss: 0.5002
Epoch 5/5
40/40 [==============================] - 0s 1ms/step - loss: 0.5007

由于神经网络和数据集规模都非常小，训练计算非常迅速。然而如果我们检查网络的预测结果，我们会发现它与我们希望找到的解相去甚远：它在x轴两侧的数据点之间取平均值，因此无法找到满意的问题解。

下面的图表清楚地展示了这一点：它显示了原始数据（绿色）和监督解（红色）。

# Results
def draw(X,Y,Y_pre):
    plt.figure(figsize=(8,5))
    plt.plot(X,Y,'.',label = 'Data Point',color='green',zorder= 1)
    plt.plot(X,Y_pre,'.',label='Supervised',color = 'red',zorder =2)
    plt.xlabel('y',fontsize = 16)
    plt.ylabel('x',fontsize = 16)
    plt.title('standard apporach',fontsize = 16)
    plt.yticks(fontproperties='Arial',size=12)
    plt.xticks(fontproperties = 'Arial',size = 12)
    plt.legend(fontsize = 12)      

y_pre = nn_sv.predict(X)
draw(X,Y,y_pre)

结果如下图所示。

这显然是完全错误的！红线与绿色解相去甚远。

请注意，红线通常不是完全接近零，而在连续的情况下，解的两个模式应该取平均值。这是由于在这个例子中只有200个采样点，采样相对粗糙造成的。

1.3 可微物理方法

现在让我们应用可微分物理方法来找到 $f$ ：直接将离散模型 $P$ 纳入训练中。这里没有真实数据生成步骤；我们只需要从 $[0, 1]$ 区间进行采样。

保持与先前情况相同的 $x$ 位置，并使用与之前架构相同的新的神经网络实例nn_dp：

# X-Data
# X = X , we can directly re-use the X from above, nothing has changed...
# Y is evaluated on the fly
# Model
nn_dp = tf.keras.models.Sequential([
tf.keras.layers.Dense(10, activation=act, input_shape=(1,)),
tf.keras.layers.Dense(10, activation=act),
tf.keras.layers.Dense(1, activation='linear')])

损失函数是训练的关键点：我们直接将函数 $f$ 融入到损失函数中。在这种简单的情况下，损失函数loss_dp只是简单地计算预测值y_pred的平方。

后来，这里可能会发生更多的事情：我们可以对预测解进行评估有限差分模板，或者计算求解器的整个隐式时间积分步长。这里我们有一个简单的均方误差项，其形式为 $∣ y_{p re d}^{2} - y_{t r u e} ∣^{2}$ ，我们在训练期间将其最小化。没有必要让它变得如此简单：我们可以结合的知识和数值方法越多，我们就能更好地指导训练过程。

#Loss
mse = tf.keras.losses.MeanSquaredError()
def loss_dp(y_true, y_pred):
    return mse(y_true,y_pred**2)

optimizer_dp = tf.keras.optimizers.Adam(learning_rate=0.001)
nn_dp.compile(optimizer= optimizer_dp,loss=loss_dp)

进行训练并显示结果：

#Training
results_dp = nn_dp.fit(X,X,epochs=5,batch_size = 5,verbose = 1)
y_pre = nn_dp.predict(X)
draw(X,Y,y_pre)

训练过程如下：

Epoch 1/5
40/40 [==============================] - 0s 656us/step - loss: 0.2814
Epoch 2/5
40/40 [==============================] - 0s 1ms/step - loss: 0.1259
Epoch 3/5
40/40 [==============================] - 0s 962us/step - loss: 0.0038
Epoch 4/5
40/40 [==============================] - 0s 949us/step - loss: 0.0014
Epoch 5/5
40/40 [==============================] - 0s 645us/step - loss: 0.0012

现在，网络实际上已经学会了抛物线函数的一个很好的反函数！下图用红色点显示计算解。

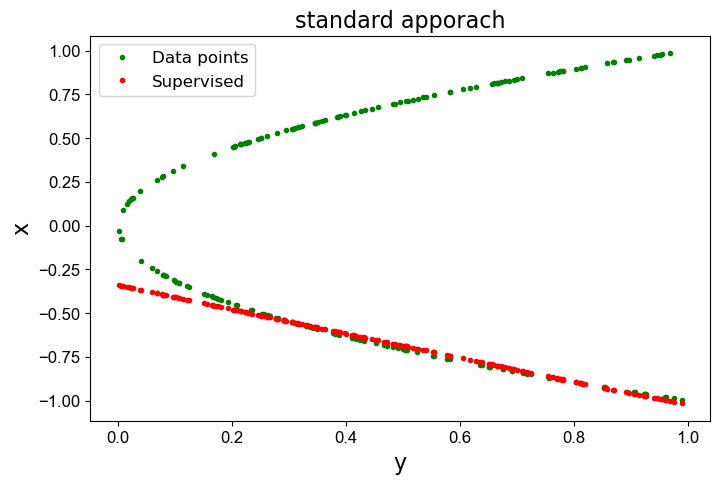
注意，红色的线可能是在上面，也可能是在下面，多次训练可能会得到不同的结果。比如出现下图的结果。

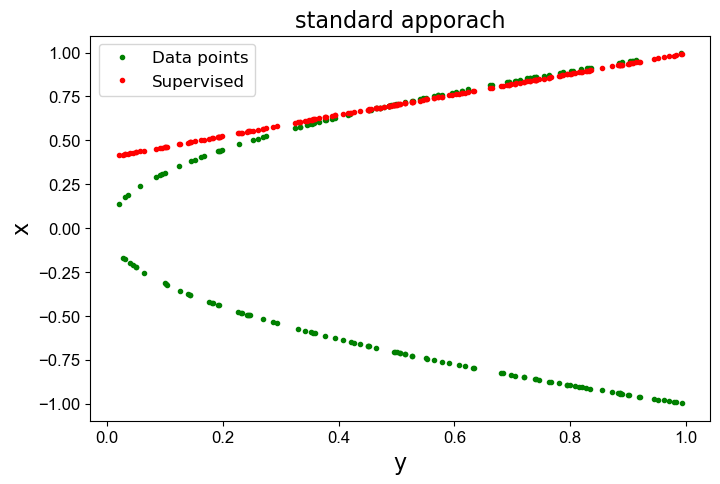
现在得到的结果要好多了。

这里发生了什么？

我们根据当前的网络预测值来评估离散模型，而不是使用预先计算好的解，从而避免了在求解中出现不希望出现的多种模式平均化现象。这样，我们就能在网络预测附近找到最佳模式，并防止求解流形中存在的模式平均化。
我们仍然只能得到曲线的一边！这是意料之中的，因为我们使用的是一个确定性函数来表示解。因此我们只能表示单一模式。有趣的是，是顶部模式还是底部模式由 $f$ 中权重的随机初始化决定的，多运行几次示例就能看到这种效果。要捕捉多种模式，我们需要扩展 NN 以捕捉输出的完整分布，并用额外的维度对其进行参数化。
在本例中， $x$ 接近零的区域通常仍然是偏离的。在这里，网络基本上学习的是抛物线一半的线性近似值。造成这种情况的部分原因是神经网络的弱点：它非常小且浅。此外沿 x 轴均匀分布的样本点会使神经网络偏向于较大的 y 值。这些点对损失的贡献更大，因此网络会投入大部分资源来减少这一区域的误差。

1.4 讨论

这是一个非常简单的例子，但却非常清晰地展示了监督学习的失败案例。虽然乍一看似乎很不真实，但许多实际的 PDE 都会表现出各种各样的这些模式，而且我们通常并不清楚我们感兴趣的解空间中存在哪些模式以及它们的位置。在这种情况下使用监督学习是非常危险的，我们可能会在不知不觉中得到这些不同模式的平均值。

流体流动中的分岔就是一个明显的好例子。蜡烛上方升起的烟雾一开始是直的，然后由于其运动中的微小扰动，开始向随机方向摆动。下面的图片通过数值扰动说明了这种情况：完全对称的设置会开始向左或向右转动，这取决于近似误差如何积累。如果将这两种模式平均化，就会产生与上述抛物线示例类似的非物理直线流。

同样，我们在许多数值解中都有不同的模式，通常重要的是恢复它们，而不是将它们平均化。因此在接下来的章节中，我们将展示如何通过可微分物理来处理更实际、更复杂的情况。

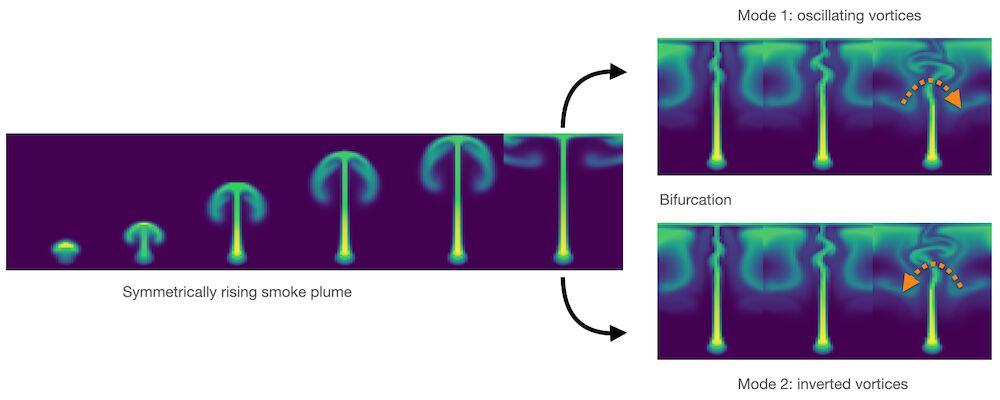
图2：浮力驱动的流体流动中的分叉：绿色显示的“烟雾”开始以完全直线的方式上升，但随着时间的推移，微小的数值误差增长，导致涡旋向一侧（右上角）或相反方向（右下角）交替的不稳定性。

图2显示浮力驱动的流体流动中的分叉：绿色显示的“烟雾”开始以完全直线的方式上升，但随着时间的推移，微小的数值误差增长，导致涡旋向一侧（右上角）或相反方向（右下角）交替的不稳定性。

1.5 下一步

下面的每本笔记本都有一个 "下一步 "部分，比如下面这个部分，其中包含了关于从哪里开始修改代码的建议。毕竟，这些笔记本的全部意义就在于提供可随时执行的程序，作为自己实验的基础。为了减少笔记本的运行时间，示例的数据集和 NN 大小通常都很小，但它们仍然是潜在复杂大型项目的良好起点。

对于上述简单的 DP 例子：

本笔记本有意使用非常简单的设置。更改上述训练设置和 NN，可以获得更高质量的解，如顶部第一张图片中显示的绿色解。
或者尝试将设置扩展到二维情况，即抛物面。给定函数 $P : (y_{1}, y_{2}) \to y_{1}^{2} + y_{2}^{2}$ ，找出一个反函数 $f$ ，使得 $[0, 1]$ 中的所有 $x$ 都能得到 $P (f (x)) = x$ 。
如果您想在不安装任何软件的情况下进行实验，也可以[在 colab 中运行此笔记本]。