对于许多实际的偏微分方程求解器来说，一个固有的挑战是问题的高维性。对于一个三维问题（其中$n$表示每个轴上的样本数），我们的模型$\mathcal{P}$通常以$\mathcal{O}(n^3)$的样本进行离散化，对于时变现象，我们还需要在时间上进行离散化。后者的规模通常与空间维度成比例。这总共导致了$\mathcal{O}(n^4)$数量级的样本数量。毫不奇怪，在这些情况下，随着$n$的增大（对于所有实际的高保真应用，我们希望$n$尽可能大），工作量迅速增加。

降低复杂性的一种流行方法是将系统的空间状态${\mathbf{s}}_{\mathbf{t}}\in {\mathbb{R}}^{n^3}$映射到一个更低维的状态${\mathbf{c}}_{\mathbf{t}}\in {\mathbb{R}}^m$，其中$m\ll n^3$。在这个潜在空间中，我们通过推断新状态${\mathbf{c}}_{\mathbf{t}+1}$来估计系统的演化，然后解码以获得${\mathbf{s}}_{\mathbf{t}+1}$。为了使这个方法奏效，关键是我们可以选择足够大的$m$来捕捉解集中的所有重要结构，并且能够高效计算${\mathbf{c}}_{\mathbf{t}+1}$的时间预测，以便尽管有额外的编码和解码步骤，仍然能够提高性能。在实践中，常规模拟中未知数的爆炸增长（上述的$\mathcal{O}(n^3)$）以及直接计算新状态${\mathbf{s}}_{\mathbf{t}}$的超线性复杂度使得这种方法非常昂贵，而使用潜在空间点$\mathbf{c}$很快就能在较小的$m$上收到回报。

然而，编码器和解码器在降低问题维度方面的表现非常重要。这对于深度学习方法来说是一个非常好的任务。此外，我们还需要对潜在空间状态$\mathbf{c}$进行时间演化，而对于大多数实际的模型方程，我们无法找到闭合形式的解来演化$\mathbf{c}$。因此，这同样对深度学习提出了一个非常好的问题。总结一下，我们面临着两个挑战：学习良好的空间编码和解码，以及学习准确的时间演化。

在下面，我们将描述一种解决这个问题的方法，该方法遵循Wiewel等人的方法{cite}wiewel2019lss和{cite}wiewel2020lsssubdiv，而这些方法又采用了Kim等人的编码器/解码器{cite}bkim2019deep。

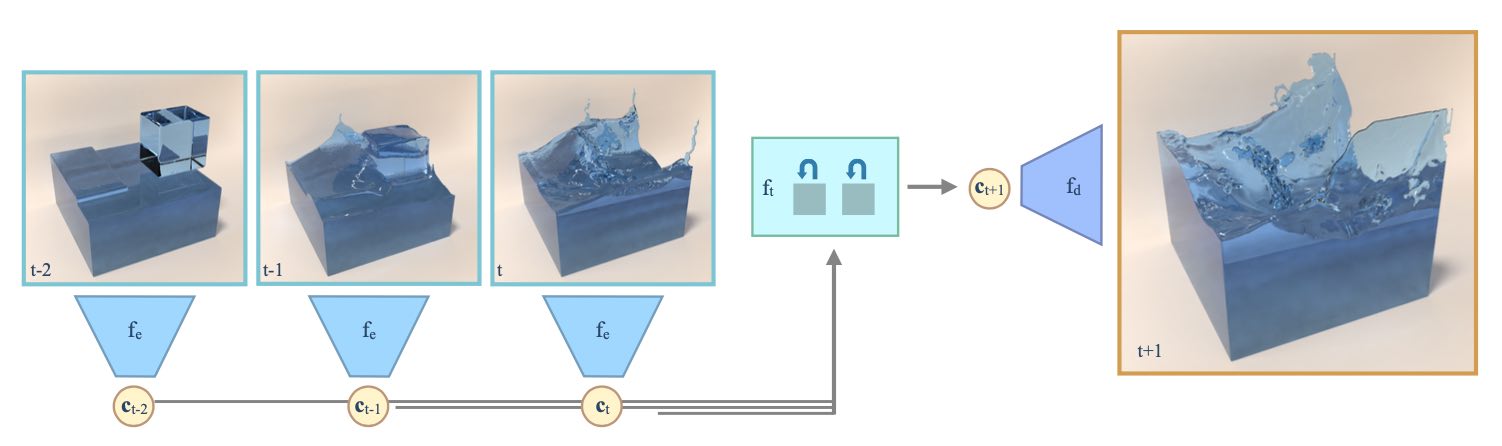
27.1 降阶模型

减少计算模型的维度和复杂性，通常被称为“降阶建模”（ROM）或“模型简化”，是计算领域的一个经典主题。传统技术通常使用主成分分析等技术来得到所选解空间的基础。然而，由于构造上的线性特性，这些方法在表示复杂的非线性解集时存在固有的局限性。在实践中，所有“有趣”的解都是高度非线性的，因此深度学习作为学习非线性表示的一种方法引起了相当大的关注。由于非线性性质，与传统方法相比，深度学习表示在降阶模型中可以以较少的自由度实现较高的精度。

用于降阶模型的经典神经网络是一个“自编码器”。这表示一个网络的唯一任务是在经过位于或接近神经网络层堆栈中间的瓶颈时重构给定的输入$x$。瓶颈处的数据表示压缩的潜在空间表示$\mathbf{c}$。通往瓶颈$\mathbf{c}$的网络部分是编码器$f_e$，而瓶颈之后的部分是解码器$f_d$。结合起来，学习任务可以写成： $${\text{arg min}}_{{\theta }_e,{\theta }_d}|f_d(f_e(\mathbf{s};{\theta }_e);{\theta }_d)-\mathbf{s}{|}_2^2$$

通过编码器$f_e:{\mathbb{R}}^{n^3}\to {\mathbb{R}}^m$（权重为${\theta }_e$）和解码器$f_d:{\mathbb{R}}^m\to {\mathbb{R}}^{n^3}$（权重为${\theta }_d$），我们可以实现这个学习目标。对于这个学习目标，我们只需要$\mathbf{s}$，不需要其他任何数据，因为它们既代表输入又代表参考输出。

自编码器网络通常由卷积层堆叠而成。虽然这些层的细节可以灵活选择，但所有自编码器架构的一个关键属性是编码器和解码器之间不能存在连接。因此，网络必须能够分离编码器和解码器。

这是合理的，因为编码器和解码器之间的任何连接（或信息共享）都将阻止以独立的方式使用编码器或解码器。例如，解码器必须能够仅通过潜在空间点$\mathbf{c}$来纯粹解码完整状态$\mathbf{s}$。

27.1.1 自动编码器变体

这里值得一提的是自编码器的一个受欢迎的变种：所谓的“变分自编码器”（Variational Autoencoders，简称VAEs）。这些自编码器遵循上述的结构，但额外采用了一个损失项来塑造潜在空间$\mathbf{c}$。其目标是让潜在空间遵循已知的分布。这使得在潜在空间中能够直接绘制样本，无需采取额外步骤，比如将样本投影到潜在空间中。

通常，我们使用正态分布作为目标，使得潜在空间成为一个$m$维的单位立方体：每个维度应具有零均值和单位标准差。这种方法在解码器需要用作生成模型时特别有用。例如，我们可以直接生成$\mathbf{c}$样本，并对其进行解码以获取完整的状态。虽然这在构建人脸或其他类型的自然图像的生成模型等应用中非常有用，但在模拟环境中并不是非常关键。在这里，我们希望获得一个能够促进时间预测的潜在空间，而不是能够轻松从中生成样本。

27.2 时间序列

时间预测的目标是根据一个或多个先前的潜在空间状态，在时间$t+1$计算出一个潜在空间状态。最直接的方式是形式化对应的最小化问题， $${\text{arg min}}_{{\theta }_p}|f_p({\mathbf{c}}_t;{\theta }_p)-{\mathbf{c}}_{t+1}{|}_2^2$$

其中预测网络被表示为$f_p$，以区别于上述的编码器和解码器。这已经意味着我们面临着一个循环任务：任何第$i$步都是通过对$f_p$进行$i$次评估得到的，即${\mathbf{c}}_{t+i}=f_p^{(i)}({\mathbf{c}}_t;{\theta }_p)$。由于每次评估都存在固有的误差，通常需要对这个过程进行多步的训练，这样$f_p$网络就能在随着时间推移产生的潜在空间状态漂移方面进行调整。

Koopman算子：在经典的动力系统文献中，对未来状态的数据驱动预测通常是以所谓的"Koopman算子"的形式来表述的，它通常采用矩阵的形式，即使用线性方法。传统的研究主要集中在获得良好的"Koopman算子"，以及与基函数结合来覆盖解空间的方法。在上面概述的方法中，$f_p$网络可以看作是一个非线性的Koopman算子。

为了使这种方法有效，我们需要适当的先前状态历史来唯一确定正确的下一个状态，或者我们的网络必须内部存储它所见过的先前状态历史。

对于前一种情况，预测网络$f_p$接收多个${\mathbf{c}}_t$。对于后一种情况，我们可以借助于循环神经网络（RNNs）子领域中的算法。已经提出了多种架构来编码和存储系统的时间状态，其中最流行的是长短期记忆（LSTM）网络、门控循环单元（GRUs）或最近的基于注意力的Transformer网络。

无论使用哪种变体，这些方法始终使用全连接层，因为潜在空间向量不具有任何空间结构，而通常表示为看似随机的值集合。由于全连接层，预测网络的参数数量迅速增长，因此需要相对较小的潜在空间维度$m$。幸运的是，这与我们在前面概述的主要目标是一致的

27.3 端到端训练

在上述的表述中，我们明确地将编码/解码和时间预测部分进行了分离。然而，在实际应用中，通常更倾向于对涉及特定任务的所有网络进行端到端的训练，因为网络可以根据任务中涉及的其他组件来调整其行为。

对于时间预测，我们可以根据$\mathbf{s}$来制定目标，并在时间预测中使用编码器和解码器来计算损失： $${\text{arg min}}_{{\theta }_e,{\theta }_p,{\theta }_d}|f_d(f_p(f_e({\mathbf{s}}_t;{\theta }_e);{\theta }_p);{\theta }_d)-{\mathbf{s}}_{t+1}{|}_2^2$$

理想情况下，这一步骤还会随着时间的推移进行展开，以稳定时间上的演化。由此产生的训练将更加昂贵，因为需要一次性训练更多的权重，并且需要处理更多的中间状态。然而，增加的成本通常会以降低整体推断误差的方式得到回报。

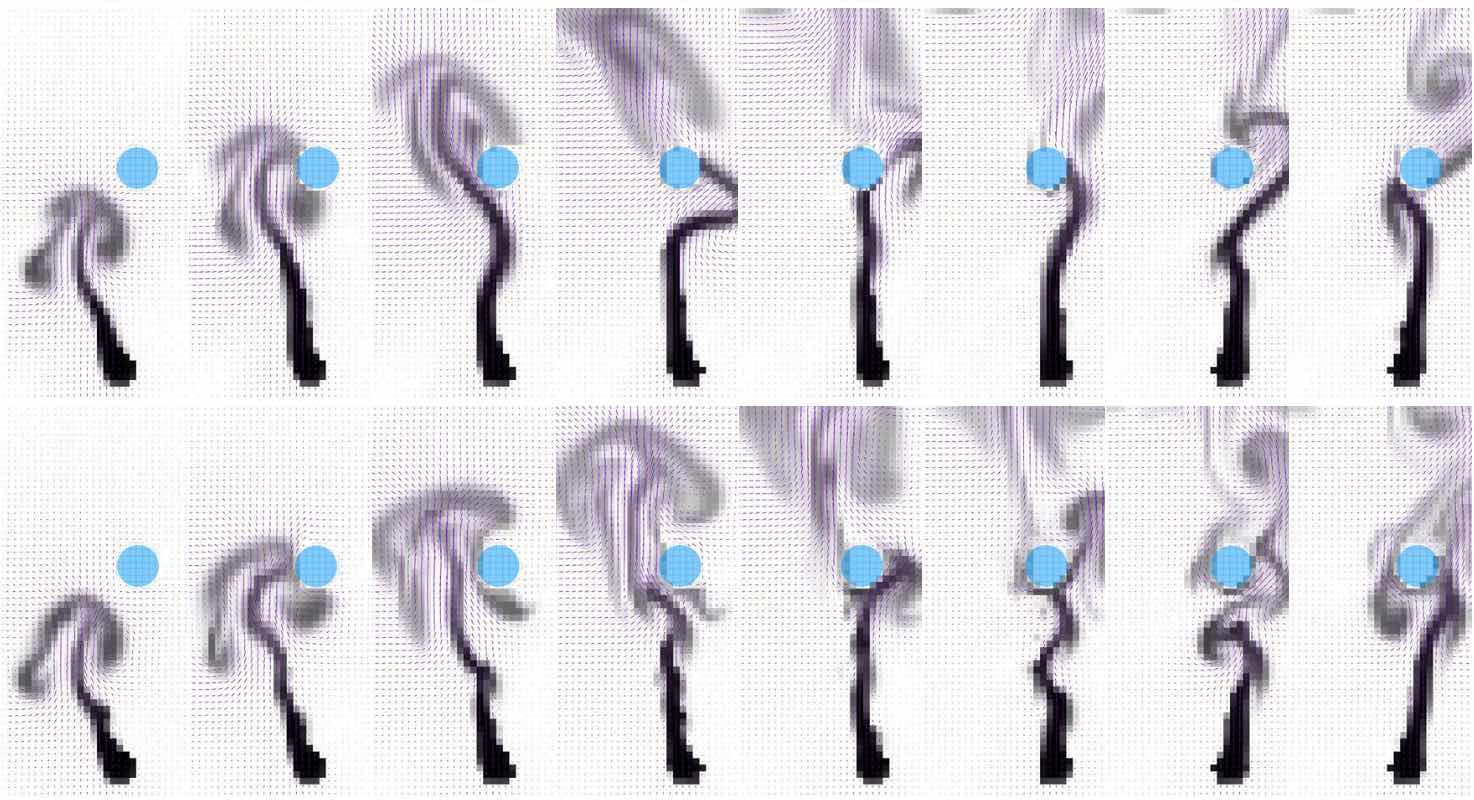
总结一下，深度学习使我们能够从线性子空间转向非线性流形，并为在生成的潜在空间中执行复杂步骤（如时间演化）提供了基础。

27.4 源代码

为了在深度学习领域进行实际实验，我们推荐使用以下两个开源代码库：潜空间模拟代码和学习模型简化代码。

这些代码库实现了端到端的训练，包括编码和预测。它们使用TensorFlow和mantaflow作为深度学习和流体模拟框架。这些代码库旨在关注编码和解码方面的内容。