前几章的尺度不变物理更新（SIP）阐明了“反演”更新步骤方向（除了利用更高阶项）的重要性。现在我们将转向另一种实现反演的方法，即所谓的“半反演梯度”（HIG）{cite}schnell2022hig。它们具有自己的优点和缺点，因此为基于物理的深度学习任务计算改进的更新步骤提供了有趣的替代方案。

与SIP不同，它们不需要解析反演求解器。HIG同时反演神经网络部分和物理模型。作为缺点，它们需要对大型雅可比矩阵进行奇异值分解。

更具体地说，HIGs（Hierarchical Inverse Graphics）不需要解析逆求解器（与SIPs相比），并且它们同时对神经网络部分和物理模型进行反演。作为一个缺点，HIGs需要对一个大的雅可比矩阵进行奇异值分解，并且基于一阶信息（类似于常规梯度）。然而，与常规梯度不同的是，它们使用完整的雅可比矩阵。因此，正如我们将在下面看到的，它们通常明显优于常规的梯度下降法（GD）和Adam算法。

21.1 推导

正如在{eq}quasi-newton-update中推导逆模拟器更新时所提到的，对于常规的牛顿步骤，更新使用了逆Hessian矩阵。如果我们将其更新重写为$L^2$损失的情况下，我们得到了Gauss-Newton（GN）方法：

$$\Delta {\theta }_{\mathrm{GN}}=-\eta \left(\right(\frac{\partial y}{\partial \theta }{)}^T\cdot \left(\frac{\partial y}{\partial \theta }\right){)}^{-1}\cdot (\frac{\partial y}{\partial \theta }{)}^T\cdot (\frac{\partial L}{\partial y}{)}^T$$

对于满秩雅可比矩阵 $\partial y/\partial \theta$，其转置雅可比矩阵抵消，方程简化为：

$$\Delta {\theta }_{\mathrm{GN}}=-\eta (\frac{\partial y}{\partial \theta }{)}^{-1}\cdot (\frac{\partial L}{\partial y}{)}^T$$

这看起来更简单，但仍然需要我们求解雅可比矩阵的逆。这个雅可比矩阵通常是非方阵，并且具有导致求逆过程中出现问题的小奇异值。简单地应用高斯-牛顿等方法可能会迅速失效。然而，由于我们处理的是在训练环节中有物理求解器的情况，这些小奇异值通常与物理有关。因此，我们不希望仅仅丢弃学习信号中的这部分内容，而是尽可能保留其中的许多部分。

这激发了HIG更新方法，它采用了部分和截断的逆形式。 $$\Delta {\theta }_{\mathrm{HIG}}=-\eta \cdot (\frac{\partial y}{\partial \theta }{)}^{-1/2}\cdot (\frac{\partial L}{\partial y}{)}^T$$

在这一步骤中，通过奇异值分解计算${}^{-1/2}$的平方根，并表示为半逆。即对于矩阵$A$，我们通过奇异值分解计算其半逆，如$A^{-1/2}=V{\Lambda }^{-1/2}{U}^T$，其中$\Lambda$包含奇异值。 在这一步中，我们还可以处理小奇异值形式的数值噪声。将$\Lambda$中小于阈值$\tau$的所有元素设为零。

截断与夹紧：一开始，将奇异值夹紧到一个小值$\tau$，而不是通过将其设为零来丢弃它们，可能看起来很有吸引力。然而，与这些小奇异值相对应的奇异向量恰恰是潜在不可靠的向量。一个小的τ在求逆过程中会产生很大的贡献，因此当进行夹紧时，这些奇异向量会引发问题。因此，通过将它们的奇异值设为零来丢弃它们的内容是一个更好的主意。

使用${}^{-1/2}$的部分逆代替${}^{-1}$的完全逆有助于防止小特征值在更新步骤中产生过大的贡献。这是受Adam方法的启发，后者通过$J/(\sqrt{(}diag(J^{T}J)))$而非$J/(J^{T}J)$对搜索方向进行归一化，其中$J$是雅可比矩阵的对角线。对于Adam，由于对角线的粗略近似，这种折中是必要的。对于HIGs，我们使用完整的雅可比矩阵，因此可以进行适当的逆运算。然而，正如原始论文{cite}schnell2022hig所述，半逆运算规范化了逆运算，并为学习提供了实质性的改进，同时降低了梯度爆炸的风险。

21.2 构造雅可比矩阵

上述公式隐藏了HIG的一个重要方面：我们计算的搜索方向不仅考虑了神经网络和物理的缩放，还可以结合mini-batch中所有样本的信息。这样做的优点是可以找到最优的方向（在$L^2$意义下）来最小化损失，而不是像GD或Adam一样对方向进行平均。

为了实现这一点，将$\partial y/\partial \theta$的Jacobian矩阵从mini-batch中每个样本的个别Jacobian拼接而成。设$x_i,y_i$分别表示mini-batch中第$i$个样本的输入和输出，则最终的Jacobian通过所有的$\frac{\partial y_i}{\partial \theta }{|}_{x_i}$构建而成。 $$\frac{\partial y}{\partial \theta }:=\left(\begin{array}{c}\frac{\partial y_1}{\partial \theta }{|}_{x_1}\\ \frac{\partial y_2}{\partial \theta }{|}_{x_2}\\ ⋮\\ \frac{\partial y_b}{\partial \theta }{|}_{x_b}\end{array}\right)$$

使用${|}_{x_i}$的符号也清楚地表明了雅可比矩阵的所有部分是根据相应的输入状态进行评估的。与常规优化不同，其中较大的批次通常由于平均效果而不会有太大回报，而HIG对批次大小有更强的依赖性。它们通常从更大的小批量大小中获益。

总结一下，计算HIG更新需要评估批次的各个雅可比矩阵，对组合雅可比矩阵进行奇异值分解，截断和半逆奇异值，并通过重新组装半逆雅可比矩阵来计算更新方向。

21.3 通过 Toy 示例说明性质

这是一个展示前文提到的性质的好时机，我们将通过一个真实的例子来说明。作为学习目标，我们将考虑一个简单的二维情境，其中包含函数。

$$\hat{y}(x)=(\sin (6x),\cos (9x))\text{ 对 }x\in [-1,1]$$

以及一个缩放的损失函数

$$L(y,\hat{y};\lambda )=\frac{1}{2}(y_1-{\hat{y}}_1{)}^2+\frac{1}{2}(\lambda \cdot y_2-{\hat{y}}_2{)}^2$$

这里的$y_1$和$y_2$分别表示$y$的第一和第二个分量（与上面的小批量条目的下标$i$相对应）。注意，通过$\lambda$进行的缩放只应用于损失的第二个分量。这模拟了在物理模拟设置中常遇到的两个分量的不均匀缩放，其量可以通过$\lambda$选择。

我们将使用一个由7个神经元组成的单隐藏层的小型神经网络，其激活函数为tanh()，目标是学习$\hat{y}$。

21.4 良好条件

让我们首先看一下在$\lambda =1$的情况下，条件良好的情况。在下面的图像中，我们将比较Adam作为最流行的梯度下降代表、高斯-牛顿（GN）作为“经典”方法以及HIGs。这些方法将根据三个方面进行评估：首先，观察损失的演变是很有趣的。此外，我们还将考虑神经网络状态的神经元激活分布（稍后详细介绍）。最后，观察优化如何影响神经网络产生的目标状态（在$y$空间中）。请注意，下面的$y$空间图表仅显示一个单一但相当代表性的$x,y$对。其他两个图表显示了更大一组验证输入的数量。

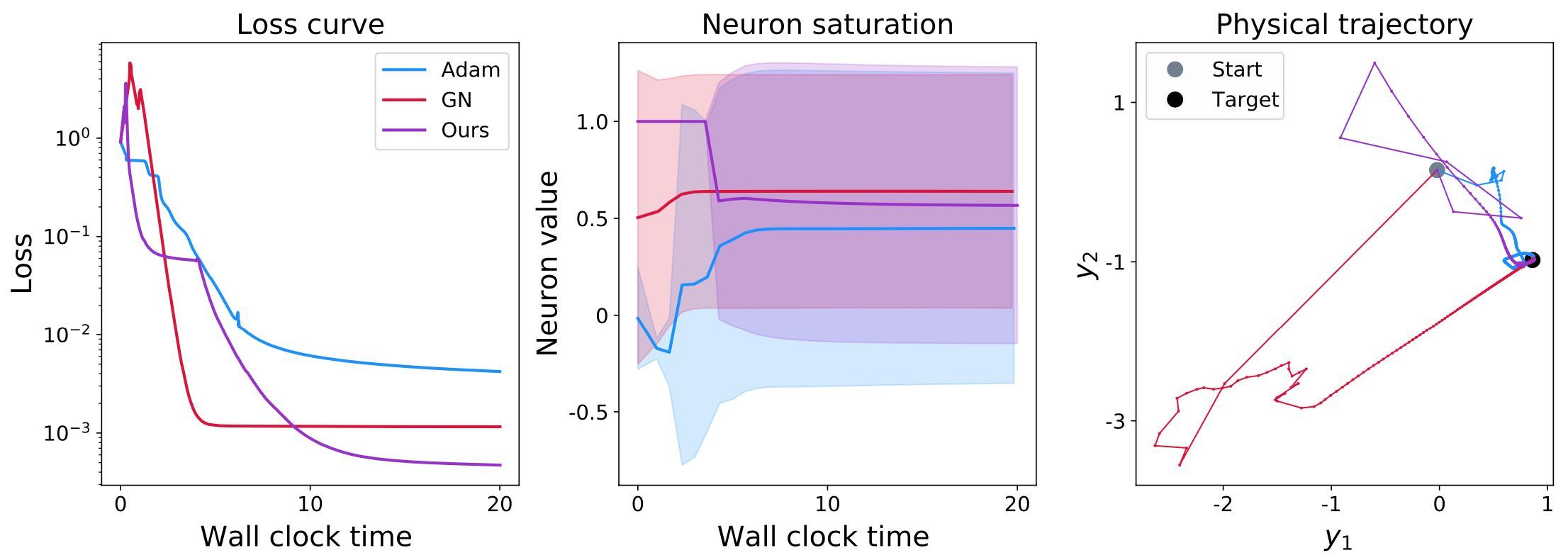
如图所示，在条件良好的情况下，所有三种方法在各个方面表现都还可以：损失降低到约$10^{-2}$和$10^{-3}$左右。

此外，神经元的激活情况（以均值和标准差表示）显示出一系列广泛的数值范围（由表示标准差的实心阴影区域表示）。这意味着所有三个网络的神经元产生了广泛的数值范围。虽然在这里很难解释具体的数值，但不同的输入产生不同的数值是一个好迹象。如果不是这种情况，即不同的输入产生恒定的数值（尽管目标$\hat{y}$显然不同），那将是一个非常不好的迹象。这通常是由于完全饱和的神经元状态被过大的更新步骤“破坏”造成的。但对于这个条件良好的示例，这种饱和现象并没有出现。

最后，右侧的第三个图显示了一个输入-输出对的演变过程。初始网络状态的起点显示为浅灰色，而地面真实目标$\hat{y}$显示为一个黑点。最重要的是，所有三种方法最终都能达到黑点。对于这个简单的示例，看到这一点并不令人过分惊讶。然而，有趣的是，GN和HIG在学习过程的初始阶段（离开灰点的前几个部分）都存在较大的跳跃。这是由于初始状态相当糟糕以及反演引起的，导致了神经网络状态及其输出的显著变化。相比之下，Adam的动量项减少了这种跳跃性：浅蓝色线条的初始跳跃比其他两种方法小。

总体而言，所有三种方法的行为基本符合我们的预期：虽然损失肯定可以进一步降低，而且$y$中的一些步骤似乎暂时朝着错误的方向发展，但这三种方法在这种情况下都表现得相当好。毫不奇怪，当使用小的$\lambda$导致条件更差的雅可比矩阵时，情况将会发生变化。

21.5 病态条件

现在我们考虑一个条件较差的情况，其中$\lambda =0.01$。在实际的PDE求解器中，情况可能会更糟，但有趣的是，这个$1/100$的因子足以说明实践中出现的问题。以下是同一组3张图的条件较差的情况：

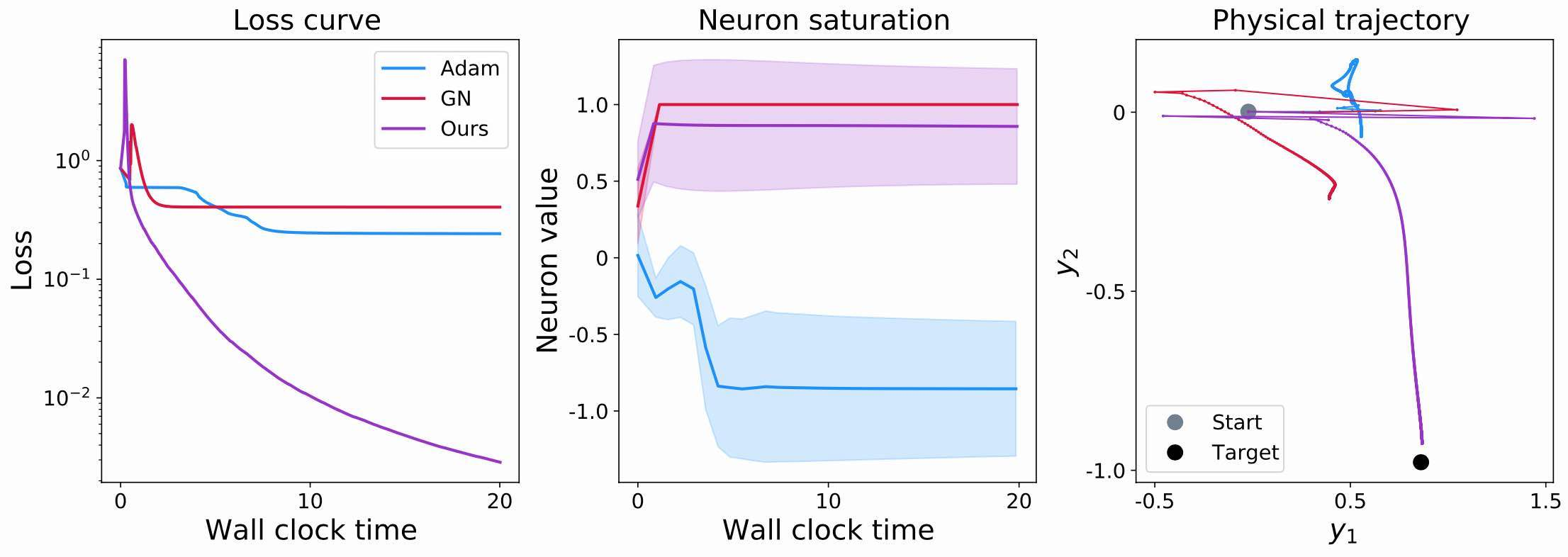
现在的损失曲线显示出不同的行为：Adam和GN都无法将损失降低到约0.2的水平以下（与之前的0.01及更好相比）。Adam在$y^2$分量的不良缩放方面存在显著问题，无法正确收敛。对于GN来说，雅可比矩阵的完全反转会导致梯度爆炸，破坏反转的积极效果。更糟糕的是，它们会导致神经网络有效地卡住。

这在中间的图表中变得更加清晰，它显示了激活统计数据。GN的红色曲线很快饱和在1处，没有显示任何方差。因此，所有的神经元都饱和了，不再产生有意义的信号。这不仅意味着目标函数没有被很好地逼近，而且意味着未来的梯度将有效地为零，并且这些神经元将在所有未来的学习迭代中丢失。因此，这是一种高度不可取的情况，我们希望在实践中避免。值得指出的是，这并不总是发生在GN上。然而，它经常发生，例如当批次中的个别样本导致雅可比矩阵中的向量线性相关（或非常接近）时，从而使GN成为次优选择。

右侧图{numref}hig-toy-example-bad的第三个图表显示了输出的结果。正如损失值所示，Adam和GN都没有达到目标（黑点）。有趣的是，它们在$y^2$方向上遇到了更多的问题，我们用它来引起不良条件：它们都在图表的x轴（$y^1$）上取得了一些进展，但在朝向$y^2$目标值方向上没有太多的移动。这说明了上面的讨论：GN由于饱和的神经元而卡住，而Adam则难以撤销$y^2$的缩放。

21.6 半逆梯度小结

请注意，到目前为止，我们已经改进了前几章中的可微物理（DP）训练的所有示例。也就是说，我们专注于神经网络和PDE求解算子的组合。后者需要在常规GD训练和HIG训练中可微分。

相反，对于使用SIPs（来自{doc}physgrad-nn）进行训练，我们甚至需要提供完整的反演求解器。正如在那里所示，这具有优势，但将SIP与DP和HIG区分开来。因此，HIG与例如{doc}diffphys-code-sol和{doc}diffphys-code-control的相似之处更多，而不是示例{doc}physgrad-code。

现在是时候给出一个具体的代码示例，展示如何使用HIG训练物理神经网络：我们将看一个经典案例，即一组耦合振子系统。