机器学习中的一个基本问题是充分表示所考虑变量 $x$ 的所有可能状态，即捕捉其完整分布。为了解决这个问题，生成对抗网络（GANs）被证明是深度学习中强大的工具。当数据存在模棱两可的解，并且没有可微分的物理模型可以消除数据的歧义时，GANs尤为重要。在这种情况下，使用监督学习会导致不希望的平均化结果，而采用GANs方法可以避免这种情况发生。

28.1 最大似然估计

为了训练生成对抗网络（GAN），我们需要简要介绍分类问题。对于这些问题，学习目标的形式与{doc}overview-equations中的方程{eq}learn-l2中的回归目标略有不同：我们现在希望最大化学习表示 $f$ 对于给定权重 $θ$ 的输入 $x_{i}$ 的概率。这导致了以下形式的最大化问题：

$arg max_{θ} Π_{i} f (x_{i}; θ)$

经典的最大似然估计（MLE）方法。实际上，通常将其转化为负对数似然之和作为学习目标：

$arg min_{θ} - i \sum log f (x_{i}; θ)$

对于这个基本表达式有许多等价的观点，例如，它可以被视为最小化经验分布与学习分布之间的KL散度。它同样表示了对训练数据定义的期望的最大化，即 $E log f (x_{i}; θ)$ 。这又可以等同于分类问题中的经典交叉熵损失，即使用Sigmoid作为激活函数的分类器。在这里的要点是，广泛使用的通过交叉熵进行训练的方法实际上是对输入概率的最大似然估计，如方程{eq}mle-prob所定义。

28.2 对抗训练

MLE是GAN中的一个关键组成部分：在这里，我们有一个生成器(generator)，通常类似于一个解码器网络，例如，来自{doc}others-timeseries的自编码器的后半部分。对于常规的GAN，生成器接收一个随机输入向量 $z$ ，并从中生成所需的输出。

然而，我们并不直接训练生成器，而是使用第二个网络作为生成器的损失函数。这个第二个网络称为鉴别器(discriminator)，它有一个分类任务：区分生成的样本和“真实”的样本。真实的样本通常以训练数据集的形式提供，下文中将用 $x$ 表示这些样本

对于常规的GAN训练，鉴别器的分类任务通常被表述为： $arg min_{θ_{d}} - \frac{1}{2} E log D (y) - \frac{1}{2} E log (1 - D (G (z))$

正如前面所述，这是对于真实样本 $y$ 和生成样本 $G (z)$ 的标准二元交叉熵训练。根据上述公式，鉴别器被训练为对于真实样本产生输出为1，对于生成样本产生输出为0，以最大化损失。

生成器损失的关键在于利用鉴别器，并生成被鉴别器认定为真实的样本： $arg min_{θ_{g}} - \frac{1}{2} E log D (G (z))$

通常情况下，这种训练是交替进行的，先进行一步 $D$ 的训练，然后进行一步 $G$ 的训练。这样一来， $D$ 网络保持不变，并为 $G$ 提供梯度，以引导 $G$ 朝着正确的方向生成与真实样本无法区分的样本。由于 $D$ 也是一个神经网络，它在构建时是可微的，能够提供必要的梯度。

28.3 正则化

由于耦合的交替训练，GAN的训练在实践中被认为是棘手的。与单一的非线性优化问题不同，现在我们有了两个相互耦合的问题，需要找到一个脆弱的平衡点。（否则，我们将面临可怕的“模式崩溃”问题：一旦其中一个网络“崩溃”为一个平凡解，耦合训练就会崩溃。）

为了缓解这个问题，正则化通常是实现稳定训练的关键。在最简单的情况下，我们可以为生成器 $G$ 添加一个关于参考数据的 $L^{1}$ 正则化项，且系数较小。沿着这个思路，以监督方式预训练生成器可以帮助 $G$ 以一个稳定的状态开始。（然而，通常情况下，鉴别器 $D$ 也需要一定程度的预训练来保持平衡。）

28.4 条件 GAN

对于物理问题来说，传统的生成对抗网络（GAN）从上述随机化的潜空间 $z$ 生成解并不是特别有用。相反，我们通常会有诸如参数、边界条件或部分解决方案等输入，这些输入应该用于推断输出。这种情况下使用的是条件GAN，也就是说，我们现在有的是 $G (x)$ 而不是 $G (z)$ ，其中 $x$ 表示输入数据。

条件生成对抗网络（conditional GANs）在超分辨率网络中扮演了重要角色：这些网络的任务是根据稀疏或低分辨率的输入解决方案来计算高分辨率的输出。

28.5 模糊解

GAN的主要优势之一是可以避免模糊数据的不良平均化。例如，考虑超分辨率的情况：一个作为输入的低分辨率观测通常有无限多个可能的高分辨率解，这些解都可以适应低分辨率输入。

如果数据集包含多个这样的情况，并且我们采用监督训练，网络将可靠地学习平均值。这种平均解通常是明显不理想的，与计算它的个别解之一完全不同。这就是多模态问题，即不同模式作为问题的等效解存在的情况。对于流体来说，这可能发生在我们面临分叉的情况下，如{doc}intro-teaser中所讨论的那样。

下面的图片清楚地展示了GAN如何很好地解决这个问题：

28.6 时空超分辨率

当然，GAN的方法并不仅限于空间分辨率。先前的工作已经证明，学习的自我监督概念可以扩展到时空解，例如，在流体模拟的超分辨率背景下 {cite}xie2018tempoGan。

下面的例子将比较不同解的时间导数：

如图所示，经过时空自我监督训练的GAN（从右数第二个）与参考解（最右边）非常接近。在这种情况下，鉴别器接收到随时间变化的参考解（以三元组的形式），从而可以学习判断生成解的时间演化是否与参考解相匹配。

28.7 物理生成模型

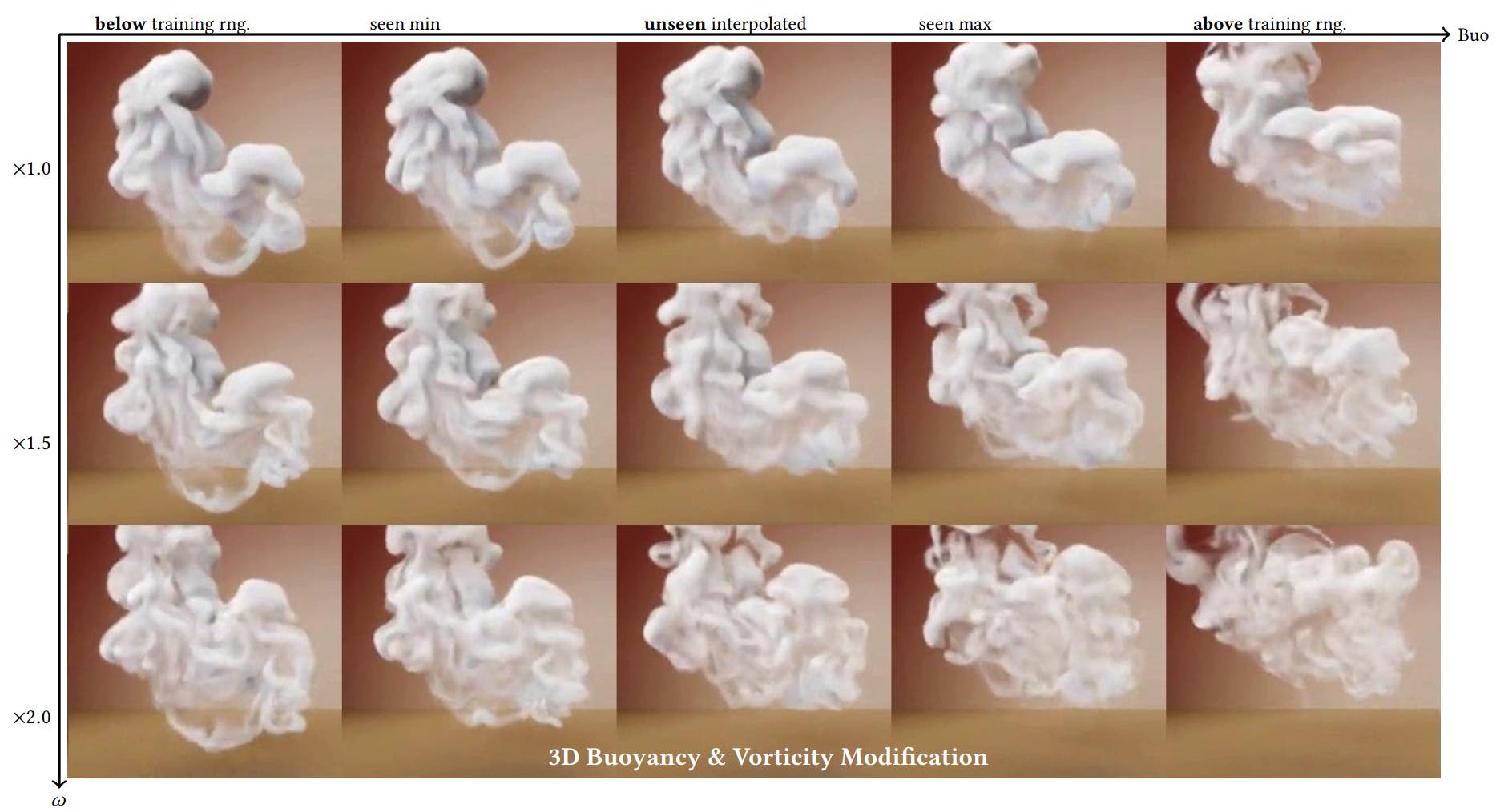
最后一个例子是，研究表明GAN也能够准确地捕捉由物理参数参数化的偏微分方程（PDEs）的解流形 {cite}chu2021physgan。在这项工作中，通过改变浮力、涡度含量、边界条件和障碍物几何形状来参数化Navier-Stokes方程的解被神经网络学习到。

这是一个极具挑战性的解决方案流形，需要一种扩展的 "循环 "GAN 方法，推动判别器考虑所有物理参数。该方法可推动判别器将所有物理参数考虑在内。有趣的是，尽管生成器是纯粹根据数据进行训练的，即不需要任何帮助，但它仍能学习生成现实而准确的解。尽管是纯粹根据数据进行训练，即没有可微分物理求解器设置的明确帮助，生成器仍能学习生成真是而准确的解。

28.8 讨论

GAN是一种强大的学习工具。需要注意的是，鉴别器 $D$ 实际上只是一个学习到的损失函数：一旦生成器完全训练好了，我们在推断阶段可以完全舍弃它。因此，它所需的资源并不是非常关键。

然而，尽管GAN是非常强大的工具，但在我们可以获得合理的PDE模型时，它是否有意义还存在疑问（根据当前的最新技术）。如果我们可以离散化模型方程并将其与可微分的物理（DP）训练结合起来（参见{doc}diffphys），那么这很可能会比使用鉴别器逼近PDE模型获得更好的结果。DP训练可以获得与GAN训练类似的好处：通过离散化的模拟器获得局部梯度，并以此方式防止对样本进行不良的平均化。因此，DP训练与GAN的组合在孤立应用时也不会表现得比它们中的任何一种更好。

话虽如此，当由于没有梯度的黑盒求解器而无法进行DP训练时，GAN仍然可能是一种有吸引力的选择。

28.9 源代码

由于训练设置的复杂性，我们只参考外部开源实现来进行物理生成对抗网络的实际实验。例如，可以在https://github.com/thunil/tempoGAN上找到{xie2018tempoGan}的时空生成对抗网络。

该实现还包括一些用于稳定性的扩展，如L1正则化和生成器-判别器平衡。