为了说明在可微分物理（DP）环境中计算梯度的过程，我们以5 PINN优化Burgers方程中 PINN 示例中使用的相同逆问题（重建任务）为目标。选择 DP 方法会产生一些直接影响：我们从离散化的 PDE 开始，系统的演化现在完全由由此产生的数值求解器决定。因此，真正的未知数只有初始状态。我们仍然需要多次重新计算初始状态和目标状态之间的所有状态，只是现在我们不需要 NN 来完成这一步骤。取而代之的是模型方程的离散化。

另外，由于我们为 DP 方法选择了一个初始离散化，未知的初始状态由涉及的物理场的采样点组成，我们可以简单地将这些未知量表示为浮点变量。因此，即使对于初始状态，我们也不需要建立神经网络。因此，使用 DP 来解决的 Burgers 重建问题简化为没有任何神经网络的基于梯度的优化。尽管如此，这仍然是一个非常好的起点来说明这个过程。

首先，我们将设置离散模拟。这里我们使用 phiflow，如Burgers forward simulations概述部分所示。

8.1 初始化

如果我们不使用 numpy 后端，phiflow 可以直接为我们提供可微分的操作序列。这里重要的一步是加入 phi.tf.flow 代替 phi.flow （对于 pytorch，可以使用 phi.torch.flow）。

因此，第一步，让我们设置一些常量，并将velocity场初始化为零，并将我们的约束条件设置为 $t = 0.5$ （步骤 16），现在作为 phiflow 中的CenteredGrid。两者都使用周期性边界条件（通过 extrapolation.PERIODIC）和 $Δ x = 1/128$ 的空间离散化。

!pip install --upgrade --quiet phiflow==2.2
from phi.tf.flow import *

N = 128
DX = 2/N
STEPS = 32
DT = 1/STEPS
NU = 0.01/(N*np.pi)

# allocate velocity grid
velocity = CenteredGrid(0, extrapolation.PERIODIC, x=N, bounds=Box(x=(-1,1)))

# and a grid with the reference solution 
REFERENCE_DATA = math.tensor([0.008612174447657694, 0.02584669669548606, 0.043136357266407785, 0.060491074685516746, 0.07793926183951633, 0.0954779141740818, 0.11311894389663882, 0.1308497114054023, 0.14867023658641343, 0.1665634396808965, 0.18452263429574314, 0.20253084411376132, 0.22057828799835133, 0.23865132431365316, 0.25673879161339097, 0.27483167307082423, 0.2929182325574904, 0.3109944766354339, 0.3290477753208284, 0.34707880794585116, 0.36507311960102307, 0.38303584302507954, 0.40094962955534186, 0.4188235294008765, 0.4366357052408043, 0.45439856841363885, 0.4720845505219581, 0.4897081943759776, 0.5072391070000235, 0.5247011051514834, 0.542067187709797, 0.5593576751669057, 0.5765465453632126, 0.5936507311857876, 0.6106452944663003, 0.6275435911624945, 0.6443221318186165, 0.6609900633731869, 0.67752574922899, 0.6939334022562877, 0.7101938106059631, 0.7263049537163667, 0.7422506131457406, 0.7580207366534812, 0.7736033721649875, 0.7889776974379873, 0.8041371279965555, 0.8190465276590387, 0.8337064887158392, 0.8480617965162781, 0.8621229412131242, 0.8758057344502199, 0.8891341984763013, 0.9019806505391214, 0.9143881632159129, 0.9261597966464793, 0.9373647624856912, 0.9476871303793314, 0.9572273019669029, 0.9654367940878237, 0.9724097482283165, 0.9767381835635638, 0.9669484658390122, 0.659083299684951, -0.659083180712816, -0.9669485121167052, -0.9767382069792288, -0.9724097635533602, -0.9654367970450167, -0.9572273263645859, -0.9476871280825523, -0.9373647681120841, -0.9261598056102645, -0.9143881718456056, -0.9019807055316369, -0.8891341634240081, -0.8758057205293912, -0.8621229450911845, -0.8480618138204272, -0.833706571569058, -0.8190466131476127, -0.8041372124868691, -0.7889777195422356, -0.7736033858767385, -0.758020740007683, -0.7422507481169578, -0.7263049162371344, -0.7101938950789042, -0.6939334061553678, -0.677525822052029, -0.6609901538934517, -0.6443222327338847, -0.6275436932970322, -0.6106454472814152, -0.5936507836778451, -0.5765466491708988, -0.5593578078967361, -0.5420672759411125, -0.5247011730988912, -0.5072391580614087, -0.4897082914472909, -0.47208460952428394, -0.4543985995006753, -0.4366355580500639, -0.41882350871539187, -0.40094955631843376, -0.38303594105786365, -0.36507302109186685, -0.3470786936847069, -0.3290476440540586, -0.31099441589505206, -0.2929180880304103, -0.27483158663081614, -0.2567388003912687, -0.2386513127155433, -0.22057831776499126, -0.20253089403524566, -0.18452269630486776, -0.1665634500729787, -0.14867027528284874, -0.13084990929476334, -0.1131191325854089, -0.09547794429803691, -0.07793928430794522, -0.06049114408297565, -0.0431364527809777, -0.025846763281087953, -0.00861212501518312] , math.spatial('x'))
SOLUTION_T16 = CenteredGrid( REFERENCE_DATA, extrapolation.PERIODIC, x=N, bounds=Box(x=(-1,1)))

下面我们将验证我们模拟的物理场现在是否得到了 TensorFlow 的支持。

type(velocity.values.native())

tensorflow.python.framework.ops.EagerTensor

8.2 梯度

phiflow的math.gradient操作生成一个用于标量损失的梯度函数，我们在下面使用它为选择的32个时间步长的整个模拟计算梯度。

为了在Burgers方程中使用它，我们需要计算一个适当的损失函数：我们希望在 $t = 0.5$ 时的解与参考数据匹配。因此，我们简单地计算步骤16和约束数组之间的 $L^{2}$ 差异作为loss。然后，我们计算初始速度状态velocity相对于该损失的梯度函数。Phiflow的math.gradient生成一个函数，该函数返回每个参数的梯度，由于我们这里只有一个速度参数，所以grad[0]表示初始速度的梯度。

def loss_function(velocity):
    velocities = [velocity]
    for time_step in range(STEPS):
        v1 = diffuse.explicit(1.0*velocities[-1], NU, DT, substeps=1)
        v2 = advect.semi_lagrangian(v1, v1, DT)
        velocities.append(v2)
    loss = field.l2_loss(velocities[16] - SOLUTION_T16)*2./N # MSE
    return loss, velocities

gradient_function = math.gradient(loss_function)

(loss,velocities), grad = gradient_function(velocity)

print('Loss: %f' % (loss))

Loss: 0.382915

因为我们只约束了第16个时间步长，所以在这个设置中我们实际上可以省略第17到31步。它们没有任何自由度，也没有受到任何约束。然而，为了与之前的情况进行公平比较，我们将它们包括在内。

请注意，我们在这里进行了很多计算：首先是32步模拟，然后是从损失开始的另外16步的反向传播。它们由梯度记录下来，并用于将损失反向传播到模拟的初始状态。

毫不奇怪，因为我们从零开始，第16个模拟步的初始误差也很大，约为0.38。

那么在这里我们得到了什么样的梯度呢？它与速度具有相同的维度，我们可以很容易地将其可视化：从零状态的velocity开始（显示为蓝色），第一个梯度显示为下方的绿线。如果将其与解进行比较，可以看到它与预期的方向相反。解的大小要大得多，因此我们在这里省略了它（请参见下一个图表）。

import pylab as plt

fig = plt.figure().gca()
pltx = np.linspace(-1,1,N)

# first gradient
fig.plot(pltx, grad[0].values.numpy('x')           , lw=2, color='green',      label="Gradient")  
fig.plot(pltx, velocity.values.numpy('x'), lw=2, color='mediumblue', label="u at t=0")
plt.xlabel('x'); plt.ylabel('u'); plt.legend();

# some (optional) other fields to plot:
# fig.plot(pltx,  (velocities[16]).values.numpy('x')   , lw=2, color='cyan', label="u at t=0.5")  
# fig.plot(pltx,  (SOLUTION_T16).values.numpy('x')   , lw=2, color='red', label="solution at t=0.5")  
# fig.plot(pltx,  (velocities[16] - SOLUTION_T16).values.numpy('x')   , lw=2, color='blue', label="difference at t=0.5")

运行结果为：

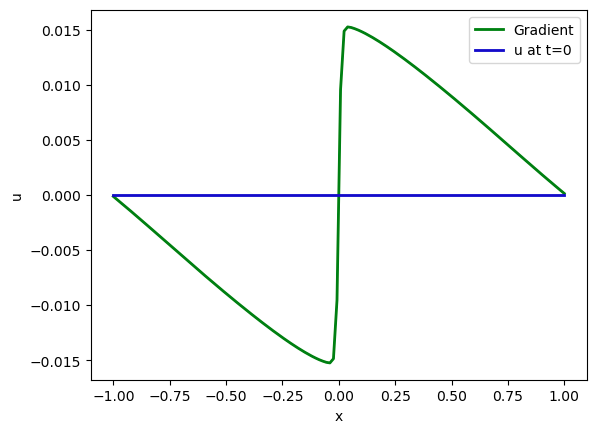
这为每个速度变量提供了一个“搜索方向”。基于线性近似，梯度告诉我们如何改变每个速度变量以增加损失函数（梯度始终指向“上方”）。因此，我们可以利用梯度进行优化，找到一个最小化损失的初始状态的速度velocity。

8.3 优化

我们现在使用梯度进行梯度下降优化。下面，我们使用学习率LR=5，并重新评估更新状态的损失以追踪收敛性。

在下面的代码块中，我们还将梯度保存在一个名为grads的列表中，以便稍后进行可视化。对于常规优化，当执行速度更新后，我们当然可以丢弃梯度。

LR = 5.

grads=[]
for optim_step in range(5):
    (loss,velocities), grad = gradient_function(velocity)
    print('Optimization step %d, loss: %f' % (optim_step,loss))
    grads.append( grad[0] )

    velocity = velocity - LR * grads[-1]

执行结果为：

Optimization step 0, loss: 0.382915
Optimization step 1, loss: 0.326882
Optimization step 2, loss: 0.281032
Optimization step 3, loss: 0.242804
Optimization step 4, loss: 0.210666

现在我们将仔细检查模拟的第16个状态是否与目标相匹配，这才是损失函数的衡量标准。下一个图表显示了约束条件（即我们希望获得的解）以绿色表示，并且在初始状态 velocity（通过梯度更新了五次）经过求解器进行了16次更新后的重构状态用蓝色表示。

fig = plt.figure().gca()

# target constraint at t=0.5
fig.plot(pltx, SOLUTION_T16.values.numpy('x'), lw=2, color='forestgreen',  label="Reference") 

# optimized state of our simulation after 16 steps
fig.plot(pltx, velocities[16].values.numpy('x'), lw=2, color='mediumblue', label="Simulated velocity")

plt.xlabel('x'); plt.ylabel('u'); plt.legend(); plt.title("After 5 Optimization Steps at t=0.5");

执行结果如下：

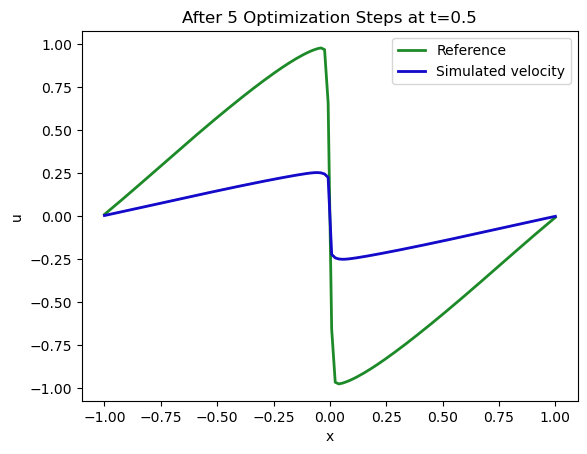
这似乎是朝着正确的方向发展！虽然还不完美，但我们目前只计算了5个梯度下降更新步骤。左侧激波上具有正速度的两个峰和右侧的负峰开始显现出来。

这是一个很好的指示，表明通过我们模拟的16个步骤反向传播的梯度表现正常，并且它正在推动解决方案朝着正确的方向发展。上面的图表只是暗示了这个设置有多么强大：我们从每个模拟步骤（以及其中的每个操作）获得的梯度可以轻松地链接成更复杂的序列。在上面的示例中，我们通过模拟的所有16个步骤进行了反向传播，通过对代码进行微小的修改，我们可以轻松地扩大这种优化的“前瞻”。

8.4 更多优化步骤

在进行更复杂的物理模拟或涉及神经网络之前，让我们先完成手头的优化任务，并运行更多步骤以获得更好的解。

import time
start = time.time()

for optim_step in range(5,50):
    (loss,velocities), grad = gradient_function(velocity)
    velocity = velocity - LR * grad[0]
    if optim_step%5==0: 
      print('Optimization step %d, loss: %f' % (optim_step,loss))

end = time.time()
print("Runtime {:.2f}s".format(end-start))

运行结果：

Optimization step 5, loss: 0.183476
Optimization step 10, loss: 0.096224
Optimization step 15, loss: 0.054792
Optimization step 20, loss: 0.032819
Optimization step 25, loss: 0.020334
Optimization step 30, loss: 0.012852
Optimization step 35, loss: 0.008185
Optimization step 40, loss: 0.005186
Optimization step 45, loss: 0.003263
Runtime 130.33s

回想一下 Burgers Optimization with a Differentiable Physics Gradient中的 PINN 版本，与可比运行时间下，误差降低了大约两个数量级。这种行为源于 DP 为具有所有离散点和时间步骤的整个解提供梯度，而不是局部更新。

让我们再次绘制我们在 $t = 0.5$ 处的解 (蓝色)与约束条件 (绿色)的匹配情况:

fig = plt.figure().gca()
fig.plot(pltx, SOLUTION_T16.values.numpy('x'), lw=2, color='forestgreen',  label="Reference") 
fig.plot(pltx, velocities[16].values.numpy('x'), lw=2, color='mediumblue', label="Simulated velocity")
plt.xlabel('x'); plt.ylabel('u'); plt.legend(); plt.title("After 50 Optimization Steps at t=0.5");

运行结果：

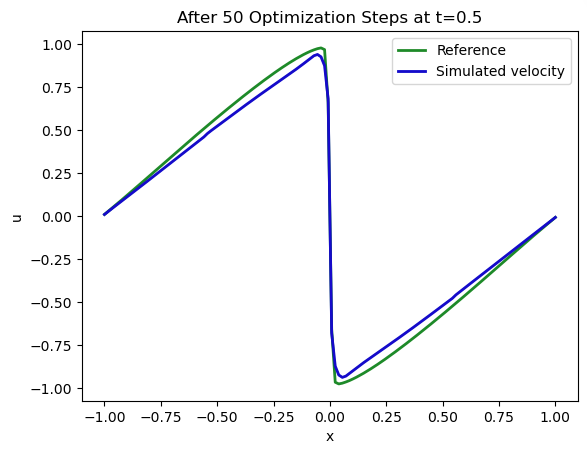
不错。但是通过 16 步模拟反向传播恢复的初始状态如何呢? 这是我们正在改变的，而且因为它只通过后期的观测结果受到间接约束，所以与期望的解或所需的解偏差的空间更大。

这在下一幅图中显示:

fig = plt.figure().gca()
pltx = np.linspace(-1,1,N)

# ground truth state at time=0 , move down
INITIAL_GT = np.asarray( [-np.sin(np.pi * x) for x in np.linspace(-1+DX/2,1-DX/2,N)] ) # 1D numpy array
fig.plot(pltx, INITIAL_GT.flatten()      , lw=2, color='forestgreen', label="Ground truth initial state")  # ground truth initial state of sim
fig.plot(pltx, velocity.values.numpy('x'), lw=2, color='mediumblue',  label="Optimized initial state") # manual
plt.xlabel('x'); plt.ylabel('u'); plt.legend(); plt.title("Initial State After 50 Optimization Steps");

结果如下所示。

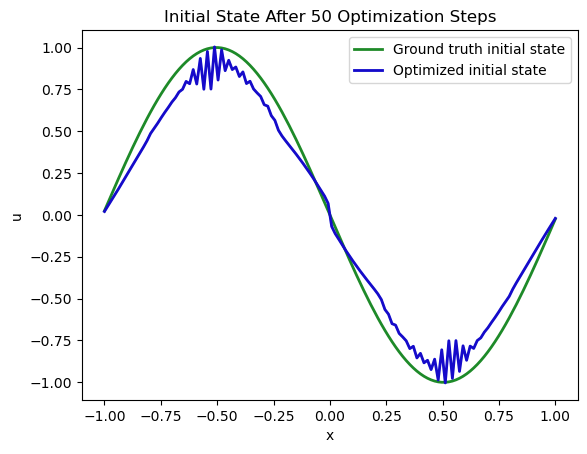
自然而然，这是一个更困难的任务：优化过程接收到了在 $t = 0.5$ 时刻状态应该是什么的直接反馈，但由于非线性模型方程的存在，通常会有大量满足约束条件的解，这些解要么完全满足约束条件，要么在数值上非常接近。因此，我们的最小化器不一定能找到我们起始状态的确切解（在默认设置下，我们可以观察到扩散算子引起的一些数值振荡）。然而，在这个Burgers场景中，解仍然非常接近。

在衡量重建的整体误差之前，让我们可视化系统随时间的完整演化，因为这也会产生一个numpy数组形式的解，我们可以与其他版本进行比较。

import pylab

def show_state(a):
    a=np.expand_dims(a, axis=2)
    for i in range(4):
        a = np.concatenate( [a,a] , axis=2)
    a = np.reshape( a, [a.shape[0],a.shape[1]*a.shape[2]] )
    fig, axes = pylab.subplots(1, 1, figsize=(16, 5))
    im = axes.imshow(a, origin='upper', cmap='inferno')
    pylab.colorbar(im) 
        
# get numpy versions of all states 
vels = [ x.values.numpy('x,vector') for x in velocities] 
# concatenate along vector/features dimension
vels = np.concatenate(vels, axis=-1) 

# save for comparison with other methods
import os; os.makedirs("./temp",exist_ok=True)
np.savez_compressed("./temp/burgers-diffphys-solution.npz", np.reshape(vels,[N,STEPS+1])) # remove batch & channel dimension

show_state(vels)

结果如下：

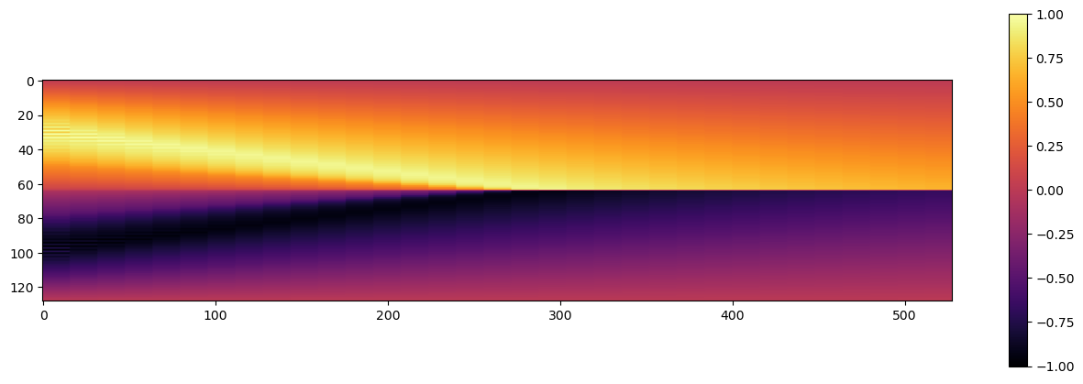
8.5 基于物理的 vs. 可微物理重建

现在我们有两个版本，一个是带有PINN的版本，另一个是DP版本，所以让我们更详细地比较这两个重建结果。（注意：以下单元格预期Burgers-forward和PINN笔记本在之前的相同环境中执行，以便./temp目录中的.npz文件可用。）

让我们首先并排查看这些解。下面的代码生成一个包含3个版本的图像，从上到下依次是：由常规正向模拟给出的真值（GT）解，中间是PINN重建，底部是可微分物理版本。

# note, this requires previous runs of the forward-sim & PINN notebooks in the same environment
sol_gt=npfile=np.load("./temp/burgers-groundtruth-solution.npz")["arr_0"] 
sol_pi=npfile=np.load("./temp/burgers-pinn-solution.npz")["arr_0"] 
sol_dp=npfile=np.load("./temp/burgers-diffphys-solution.npz")["arr_0"] 

divider = np.ones([10,33])*-1. # we'll sneak in a block of -1s to show a black divider in the image
sbs = np.concatenate( [sol_gt, divider, sol_pi, divider, sol_dp], axis=0)

print("\nSolutions Ground Truth (top), PINN (middle) , DiffPhys (bottom):")
show_state(np.reshape(sbs,[N*3+20,33,1]))

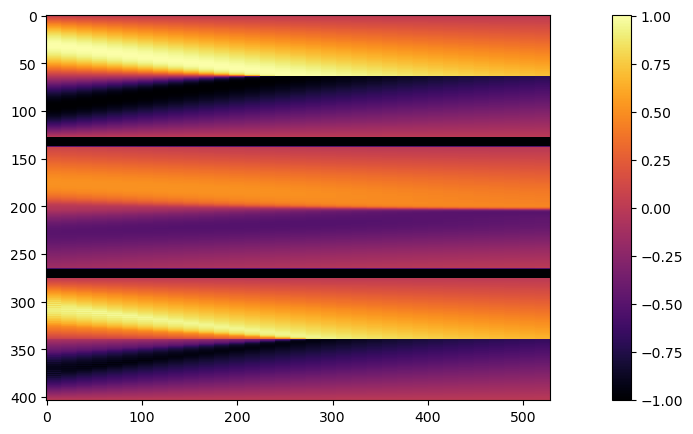
在这里很明显可以看到，PINN解决方案（中间）恢复了解的整体形状，因此时间约束至少部分得到满足。然而，它并没有很好地捕捉到GT解决方案的幅值。

与可微分求解器的优化重建（底部）相比，由于整个序列的梯度流改善，它更接近于真实情况。此外，它可以利用基于网格的离散化进行正向和反向传递，并以这种方式向未知的初始状态提供更准确的信号。然而，可以看出重建缺少GT版本的某些“更锐利”的特征，例如在解图像的左下角可见。

让我们量化整个序列的误差:

err_pi = np.sum( np.abs(sol_pi-sol_gt)) / (STEPS*N)
err_dp = np.sum( np.abs(sol_dp-sol_gt)) / (STEPS*N)
print("MAE PINN: {:7.5f} \nMAE DP:   {:7.5f}".format(err_pi,err_dp))

print("\nError GT to PINN (top) , GT to DiffPhys (bottom):")
show_state(np.reshape( np.concatenate([sol_pi-sol_gt, divider, sol_dp-sol_gt],axis=0) ,[N*2+10,33,1]))

执行结果：

MAE PINN: 0.19298 
MAE DP:   0.06382

Error GT to PINN (top) , GT to DiffPhys (bottom):

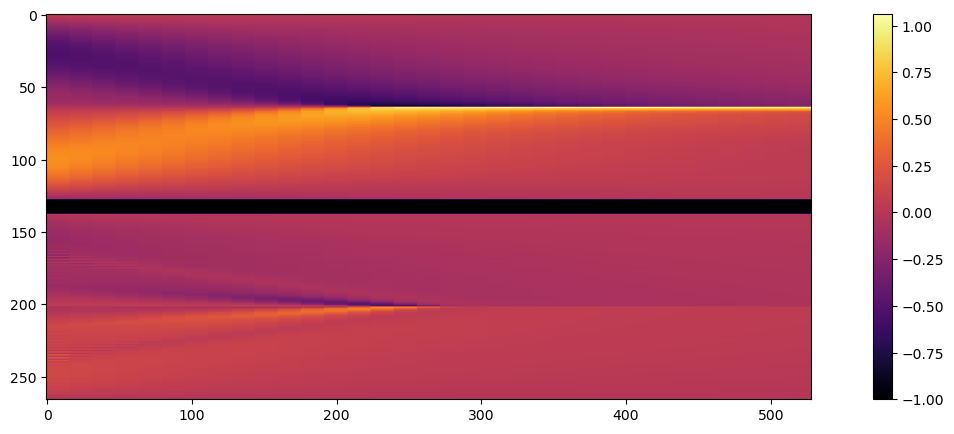
这是一个相当清晰的结果：PINN误差比可微物理（DP）重建的误差大3倍以上。

这个差异在底部的联合可视化图像中也清晰可见：DP重建的误差幅度更接近于零，如上方的紫色所示。

像这样的简单直接重建问题对于DP求解器来说总是一个很好的初始测试。在进入更复杂的设置（例如与NN耦合）之前，可以独立测试它。如果直接优化无法收敛，可能仍然存在一些根本性问题，没有必要涉及NN。

现在我们有了一个第一个示例来展示这两种方法的相似性和差异。在下一节中，我们将对迄今为止的发现进行讨论，然后在下一章中转向更复杂的情况。

8.6 下一步

与之前一样，可以使用上述代码改进和进行实验的事物有很多：

可以尝试调整训练参数以进一步改善重建效果。
激活不同的优化器，并观察收敛行为的变化（不一定是改善）。
改变步数或模拟和重建的分辨率。
尝试在loss_function之前的一行添加@jit_compile。这将增加一次编译成本，但极大地加快了优化的速度。