为了说明物理信息损失是如何在变体 2 中发挥作用的，让我们以重建任务作为反问题的例子。我们将使用Burgers方程 $\frac{\partial u}{\partial t} + u \nabla u = ν \nabla \cdot \nabla u$ 作为一个简单但非线性的一维方程，我们在时间 $t = 0.5$ 时有一系列_观测值_。解应该符合Burgers方程的残差公式，并与观测结果相匹配。此外，让我们在计算域两侧施加狄利克雷边界条件 $u = 0$ ，并将解定义在时间区间 $t \in [0, 1]$ 上。

请注意，与之前的正向模拟示例类似，我们仍将使用 128 个点（ $n = 128$ ）对解进行采样，但现在我们通过 NN 进行了离散化。因此，我们也可以对中间的点进行采样，而无需明确选择用于插值的基函数。现在通过 NN 进行离散化，可以在内部决定如何使用其自由度来安排激活函数作为基函数。因此，我们无法直接控制重构。

5.1 原理

根据 2.5 模型与方程和前一节中的 $x, y^{*}$ 符号，这个重构问题意味着我们要求解的是： $arg min_{θ} i \sum (f (x_{i}; θ) - y_{i}^{*})^{2} + R (x_{i}),$

其中 $x_{i}$ 表示时空点 $x_{i} = [p_{i}, t_{i}]$ ，参考解为 $y_{i}^{*} = y^{*} (x_{i})$ ，索引 $i$ 表示数据集的不同采样点。 $f$ 和 $y^{*}$ 都表示 $u$ 在空间和时间的不同位置的解，由于我们处理的是一维速度，所以 $f, y^{*} ： R^{2} \to R$ 。在这个例子中， $y^{*}$ 表示布尔格斯方程 $P$ 的参考值 $u$ ，在所有选定的时空点 $x_{i} = [p_{i}, t_{i}]$ 上， $f$ 应尽可能接近这个参考值。

上述第一项是 "监督 "数据项，第二项表示残差函数 $R$ 。它收集了 $f (; θ)$ 及其导数的额外评估，以计算 $P$ 的残差。这种方法--使用神经网络的导数来计算PDE残差--通常被称为_physics-informed_方法，产生一个physics-informed神经网络（PINN）[RPK19] 来表示逆重建问题的解。

上述残差函数 $R$ 收集 $f (; θ)$ 及其导数的其他评估值以构建 $P$ 的残差。这种方法——使用神经网络的导数来计算PDE残差——通常称为物理信息(physicals-informed)方法，产生一个物理信息神经网络(PINN)来表示反演重构问题的解。

因此，在上述公式中， $R$ 应简单地收敛为零。为简单起见，我们省略了目标函数中的缩放因子。请注意，实际上我们在这里处理的只是 $P$ 的单个解 $u$ 的单点样本。

5.2 准备工作

现在我们先用 tensorflow 后端加载 phiflow，然后初始化随机采样。(注：本例使用的是旧版本 1.5.1 的 phiflow）。

!pip install --quiet phiflow==1.5.1

from phi.tf.flow import *
import numpy as np

#rnd = TF_BACKEND  # for phiflow: sample different points in the domain each iteration
rnd = math.choose_backend(1)  # use same random points for all iterations

注：在python3.9之后，优于collections.Iterable被废弃，第7行语句会报错。这里需要打开文件C:\ProgramData\anaconda3\Lib\site-packages\phi\backend\scipy_backend.py，修改第37行为 if isinstance(values, collections.abc.Iterable):，注意重启内核。

我们在这里导入了 phiflow，但不会像Simple Forward Simulation of Burgers Equation with phiflow中那样用它来计算 PDE 的解。相反，我们将使用 NN 的导数（如上一节所述）来为训练设置损失公式。

接下来，我们建立了一个简单的NN，其中包含8个完全连接的层和每个20个单元的tanh激活。

我们还将定义 boundary_tx 函数和 open_boundary 函数，前者给出解的约束条件数组（本例中所有约束条件均为 $= 0.5$ ），后者存储 $x = \pm 1$ 为 0 的约束条件。

def network(x, t):
    """ Dense neural network with 8 hidden layers and 3021 parameters in total.
        Parameters will only be allocated once (auto reuse).
    """
    y = math.stack([x, t], axis=-1)
    for i in range(8):
        y = tf.layers.dense(y, 20, activation=tf.math.tanh, name='layer%d' % i, reuse=tf.AUTO_REUSE)
    return tf.layers.dense(y, 1, activation=None, name='layer_out', reuse=tf.AUTO_REUSE)

def boundary_tx(N):
    x = np.linspace(-1,1,128)
    # precomputed solution from forward simulation:
    u = np.asarray( [0.008612174447657694, 0.02584669669548606, 0.043136357266407785, 0.060491074685516746, 0.07793926183951633, 0.0954779141740818, 0.11311894389663882, 0.1308497114054023, 0.14867023658641343, 0.1665634396808965, 0.18452263429574314, 0.20253084411376132, 0.22057828799835133, 0.23865132431365316, 0.25673879161339097, 0.27483167307082423, 0.2929182325574904, 0.3109944766354339, 0.3290477753208284, 0.34707880794585116, 0.36507311960102307, 0.38303584302507954, 0.40094962955534186, 0.4188235294008765, 0.4366357052408043, 0.45439856841363885, 0.4720845505219581, 0.4897081943759776, 0.5072391070000235, 0.5247011051514834, 0.542067187709797, 0.5593576751669057, 0.5765465453632126, 0.5936507311857876, 0.6106452944663003, 0.6275435911624945, 0.6443221318186165, 0.6609900633731869, 0.67752574922899, 0.6939334022562877, 0.7101938106059631, 0.7263049537163667, 0.7422506131457406, 0.7580207366534812, 0.7736033721649875, 0.7889776974379873, 0.8041371279965555, 0.8190465276590387, 0.8337064887158392, 0.8480617965162781, 0.8621229412131242, 0.8758057344502199, 0.8891341984763013, 0.9019806505391214, 0.9143881632159129, 0.9261597966464793, 0.9373647624856912, 0.9476871303793314, 0.9572273019669029, 0.9654367940878237, 0.9724097482283165, 0.9767381835635638, 0.9669484658390122, 0.659083299684951, -0.659083180712816, -0.9669485121167052, -0.9767382069792288, -0.9724097635533602, -0.9654367970450167, -0.9572273263645859, -0.9476871280825523, -0.9373647681120841, -0.9261598056102645, -0.9143881718456056, -0.9019807055316369, -0.8891341634240081, -0.8758057205293912, -0.8621229450911845, -0.8480618138204272, -0.833706571569058, -0.8190466131476127, -0.8041372124868691, -0.7889777195422356, -0.7736033858767385, -0.758020740007683, -0.7422507481169578, -0.7263049162371344, -0.7101938950789042, -0.6939334061553678, -0.677525822052029, -0.6609901538934517, -0.6443222327338847, -0.6275436932970322, -0.6106454472814152, -0.5936507836778451, -0.5765466491708988, -0.5593578078967361, -0.5420672759411125, -0.5247011730988912, -0.5072391580614087, -0.4897082914472909, -0.47208460952428394, -0.4543985995006753, -0.4366355580500639, -0.41882350871539187, -0.40094955631843376, -0.38303594105786365, -0.36507302109186685, -0.3470786936847069, -0.3290476440540586, -0.31099441589505206, -0.2929180880304103, -0.27483158663081614, -0.2567388003912687, -0.2386513127155433, -0.22057831776499126, -0.20253089403524566, -0.18452269630486776, -0.1665634500729787, -0.14867027528284874, -0.13084990929476334, -0.1131191325854089, -0.09547794429803691, -0.07793928430794522, -0.06049114408297565, -0.0431364527809777, -0.025846763281087953, -0.00861212501518312] );
    t = np.asarray(rnd.ones_like(x)) * 0.5
    perm = np.random.permutation(128) 
    return (x[perm])[0:N], (t[perm])[0:N], (u[perm])[0:N]

def _ALT_t0(N): # alternative, impose original initial state at t=0
    x = rnd.random_uniform([N], -1, 1)
    t = rnd.zeros_like(x)
    u = - math.sin(np.pi * x)
    return x, t, u

def open_boundary(N):
    t = rnd.random_uniform([N], 0, 1)
    x = math.concat([math.zeros([N//2]) + 1, math.zeros([N//2]) - 1], axis=0)
    u = math.zeros([N])
    return x, t, u

最重要的是，我们现在还可以构建我们希望最小化的残差损失函数f，以便引导 NN 为我们的模型方程获取一个解。从最上面的方程中可以看出，我们需要与 $t$ 、 $x$ 相关的导数以及 $x$ 的二次导数。下面 f 的前三行就是这样做的。

之后，我们只需将导数结合起来，就能形成Burgers方程。这里我们使用 phiflow 的 gradient函数：

def f(u, x, t):
    """ Physics-based loss function with Burgers equation """
    u_t = gradients(u, t)
    u_x = gradients(u, x)
    u_xx = gradients(u_x, x)
    return u_t + u*u_x - (0.01 / np.pi) * u_xx

接下来，让我们在内域中设置采样点，以便将解与之前在 phiflow 中进行的正向模拟进行比较。

下面的单元格分配两个张量:grid_x将使用128个单元覆盖我们的域，即-1到1的范围，而grid_t将使用33个时间点对时间区间 $[0 ， 1]$ 进行采样。

最后的math.expand_dims()调用只是添加了一个batch维度，这样得到的张量与下面的示例兼容。

N=128
grids_xt = np.meshgrid(np.linspace(-1, 1, N), np.linspace(0, 1, 33), indexing='ij')
grid_x, grid_t = [tf.convert_to_tensor(t, tf.float32) for t in grids_xt]

# create 4D tensor with batch and channel dimensions in addition to space and time
# in this case gives shape=(1, N, 33, 1)
grid_u = math.expand_dims(network(grid_x, grid_t))

现在，grid_u包含一个完整的图，用于在 $128 \times 33$ 个位置上评估我们的NN，一旦我们通过session.run运行它，就会以 $[1 ， 128 ， 33 ， 1]$ 数组的形式返回结果。让我们试一试：我们可以初始化一个 TF 会话，评估 grid_u 并将其显示在图像中，就像我们之前计算的 phiflow 解一样。

(注意，我们将使用Simple Forward Simulation of Burgers Equation with phiflow中的 show_state。因此，X 轴并不显示实际的模拟时间，而是显示被放大16倍的32个时间步，以使图像中随时间变化更容易看到。)

import pylab as plt
print("Size of grid_u: "+format(grid_u.shape))

session = Session(None)
session.initialize_variables()

def show_state(a, title):
    for i in range(4): a = np.concatenate( [a,a] , axis=3)
    a = np.reshape( a, [a.shape[1],a.shape[2]*a.shape[3]] )
    fig, axes = plt.subplots(1, 1, figsize=(16, 5))
    im = axes.imshow(a, origin='upper', cmap='inferno')
    plt.colorbar(im) ; plt.xlabel('time'); plt.ylabel('x'); plt.title(title)
    
print("Randomly initialized network state:")
show_state(session.run(grid_u),"Uninitialized NN")

运行输出为：

Size of grid_u: (1, 128, 33, 1)
Randomly initialized network state:

这种可视化效果已经显示出空间和时间上的平滑过渡。到目前为止，这纯粹是我们正在采样的 NN 的随机初始化。因此，到目前为止，它与我们基于 PDE 模型的解决方案毫无关系。接下来的步骤将根据数据（来自boundary函数）和来自f的模型约束条件对约束条件进行实际评估，以获取 PDE 的实际解。

5.3 损失函数和训练

作为学习过程的目标，我们现在可以将direct 约束条件，即 $t = 0.5$ 时的解和狄利克雷 $u = 0$ 边界条件与来自 PDE 残差的损失结合起来。对于这两个边界约束条件，我们将在下方使用 100 个点，然后在内部区域使用额外的 1000 个点对解进行采样。

直接约束通过 network(x, t)[:, 0] - u 进行评估，其中 x 和 t 是我们希望对解进行采样的时空位置，而 u 则提供相应的真值。

对于物理损失点，我们没有真值解，但我们只需通过 NN 导数评估 PDE 残差，看看解是否满足 PDE 模型。如果不满足，就会直接产生误差，需要在优化过程中通过更新步骤来减少误差。相应的表达式如下f(network(x, t)[:, 0], x, t)。请注意，对于数据和物理项，network()[:, 0]表达式不会从 $L^{2}$ 评估中删除任何数据，它们只是丢弃了网络返回的 $(n, 1)$ 张量的最后一个 size-1 维。

# Boundary loss
N_SAMPLE_POINTS_BND = 100
x_bc, t_bc, u_bc = [math.concat([v_t0, v_x], axis=0) for v_t0, v_x in zip(boundary_tx(N_SAMPLE_POINTS_BND), open_boundary(N_SAMPLE_POINTS_BND))]
x_bc, t_bc, u_bc = np.asarray(x_bc,dtype=np.float32), np.asarray(t_bc,dtype=np.float32) ,np.asarray(u_bc,dtype=np.float32)
#with app.model_scope():
loss_u = math.l2_loss(network(x_bc, t_bc)[:, 0] - u_bc)  # normalizes by first dimension, N_bc

# Physics loss inside of domain
N_SAMPLE_POINTS_INNER = 1000
x_ph, t_ph = tf.convert_to_tensor(rnd.random_uniform([N_SAMPLE_POINTS_INNER], -1, 1)), tf.convert_to_tensor(rnd.random_uniform([N_SAMPLE_POINTS_INNER], 0, 1))
loss_ph = math.l2_loss(f(network(x_ph, t_ph)[:, 0], x_ph, t_ph))  # normalizes by first dimension, N_ph

# Combine
ph_factor = 1.
loss = loss_u + ph_factor * loss_ph # allows us to control the relative influence of loss_ph 

optim = tf.train.GradientDescentOptimizer(learning_rate=0.02).minimize(loss)
#optim = tf.train.AdamOptimizer(learning_rate=0.001).minimize(loss) # alternative, but not much benefit here

上面的代码只是初始化了损失的评估，我们仍然没有进行任何优化步骤，但我们终于可以开始着手处理这个问题了。

尽管方程很简单，但收敛速度通常很慢。迭代本身的计算速度很快，但这种设置需要大量的迭代。为了将运行时间控制在合理范围内，我们默认只进行 10k 次迭代 (ITERS)。你可以增加这个值，以获得更好的结果。

session.initialize_variables()

import time
start = time.time()

ITERS = 10000
for optim_step in range(ITERS+1):
  _, loss_value = session.run([optim, loss])
  if optim_step<3 or optim_step%1000==0: 
        print('Step %d, loss: %f' % (optim_step,loss_value))
        #show_state(grid_u)
        
end = time.time()
print("Runtime {:.2f}s".format(end-start))

Step 0, loss: 0.276599
Step 1, loss: 0.155847
Step 2, loss: 0.125085
Step 1000, loss: 0.053451
Step 2000, loss: 0.050352
Step 3000, loss: 0.047439
Step 4000, loss: 0.045276
Step 5000, loss: 0.042576
Step 6000, loss: 0.040332
Step 7000, loss: 0.036957
Step 8000, loss: 0.031184
Step 9000, loss: 0.028826
Step 10000, loss: 0.027606
Runtime 33.19

训练可能需要相当长的时间，在典型的notebook上大约需要2分钟，但至少误差显著下降(从约0.2降低到约0.03)，网络似乎成功地收敛到一个解。

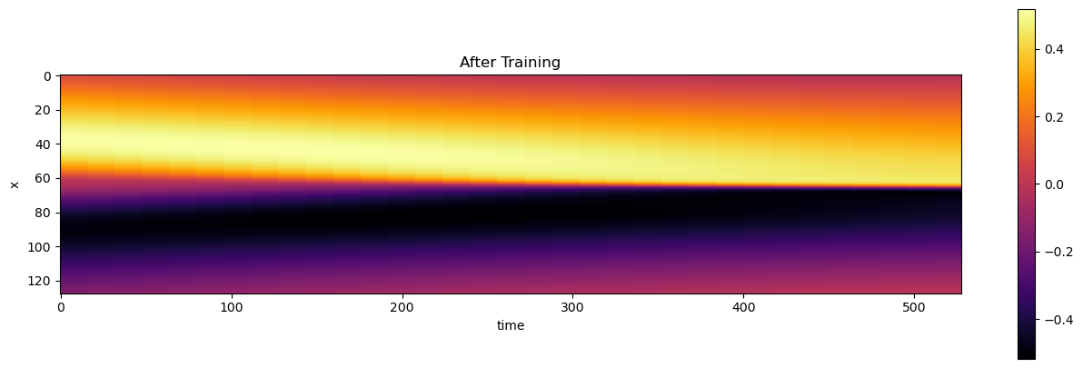
让我们通过在规则网格的中心评估网络来显示网络的重构，这样我们就可以将解显示为图像。请注意，这实际上相当昂贵，我们必须对所有的 $128 \times 32$ 个采样点运行整个网络及其几千个权重。

不过，乍一看它看起来相当不错。与上面显示的随机初始化相比，发生了非常明显的变化:

5.4 评估

让我们更详细地比较一下解法。下面是用于约束解法的实际样本点（时间步长为 16， $t = 1/2$ ）（灰色）和重构解法（蓝色）：

u = session.run(grid_u)

# solution is imposed at t=1/2 , which is 16 in the array
BC_TX = 16 
uT = u[0,:,BC_TX,0]

fig = plt.figure().gca()
fig.plot(np.linspace(-1,1,len(uT)), uT, lw=2, color='blue', label="NN")
fig.scatter(x_bc[0:100], u_bc[0:100], color='gray', label="Reference")
plt.title("Comparison at t=1/2")
plt.xlabel('x'); plt.ylabel('u'); plt.legend()

反馈结果为：

<matplotlib.legend.Legend at 0x7f8eca2a7a00>

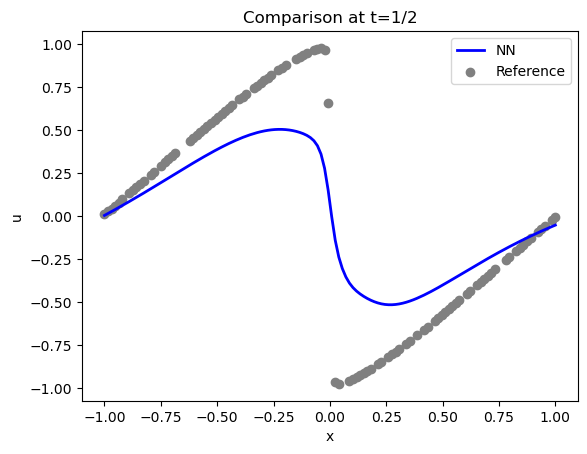
域两侧的情况还不错（满足了 Dirichlet 边界条件 $u = 0$ ），但中心（位于 $x = 0$ ）的激波没有得到很好的表现。

让我们来看看 $t = 0$ 时的初始状态重建得如何。这是最有趣、也是最棘手的部分（其余部分基本上都是根据模型方程和边界条件，给出第一种状态）。

事实证明，初始状态的精确度其实并不高：PINN 的蓝色曲线与参考数据（灰色显示）的约束条件相去甚远...随着迭代次数的增加，求解结果会越来越好，但对于这种相当简单的情况来说，迭代次数之多令人吃惊。

# ground truth solution at t0
t0gt = np.asarray( [ [-math.sin(np.pi * x) * 1.] for x in np.linspace(-1,1,N)] )
velP0 = u[0,:,0,0]

fig = plt.figure().gca()
fig.plot(np.linspace(-1,1,len(velP0)), velP0, lw=2, color='blue', label="NN")
fig.plot(np.linspace(-1,1,len(t0gt)), t0gt, lw=2, color='gray', label="Reference") 
plt.title("Comparison at t=0")
plt.xlabel('x'); plt.ylabel('u'); plt.legend()

运行结果为：

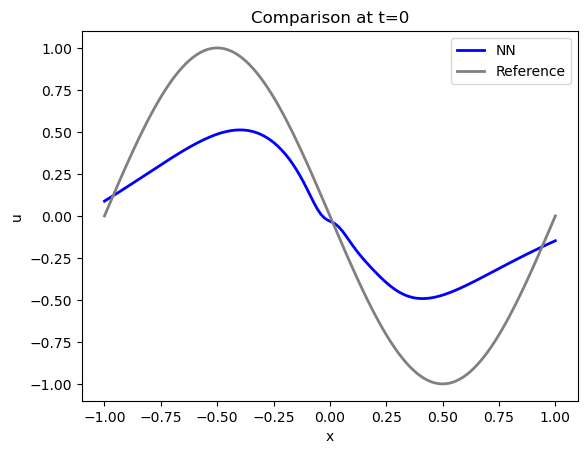
尤其是 $x = \pm 1/2$ 处的最大值/最小值相差甚远，而 $x = \pm 1$ 处的边界不符合要求：解不为零。

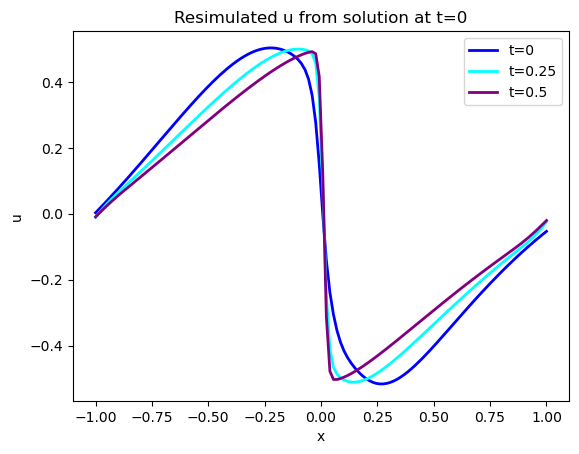
我们有用于该模拟的前向模拟器，因此我们可以使用网络的 $t = 0$ 解来评估时间评估的重建效果。这可以衡量通过 PINN 损失的软约束捕捉模型方程时间演化的程度。

下图显示了蓝色的初始状态，以及在 $t = 8/32$ 和 $t = 15/32$ 时的两个演化状态。请注意，这些都是模拟版本，接下来我们将展示学习版本。

(注：下面的代码段还有一些可选代码，用于显示[STEPS//4]处的状态。默认情况下这些代码都已注释，如果你愿意，可以取消注释或添加额外的代码，以显示更多的时间演化过程）。

# re-simulate with phiflow from solution at t=0
DT = 1./32.
STEPS = 32-BC_TX # depends on where BCs were imposed
INITIAL = u[...,BC_TX:(BC_TX+1),0] # np.reshape(u0, [1,len(u0),1]) 
print(INITIAL.shape)

DOMAIN = Domain([N], boundaries=PERIODIC, box=box[-1:1])
state = [BurgersVelocity(DOMAIN, velocity=INITIAL, viscosity=0.01/np.pi)]
physics = Burgers()

for i in range(STEPS):
    state.append( physics.step(state[-1],dt=DT) )

# we only need "velocity.data" from each phiflow state
vel_resim = [x.velocity.data for x in state]

fig = plt.figure().gca()
pltx = np.linspace(-1,1,len(vel_resim[0].flatten()))
fig.plot(pltx, vel_resim[ 0].flatten(),       lw=2, color='blue',  label="t=0")
#fig.plot(pltx, vel_resim[STEPS//4].flatten(), lw=2, color='green', label="t=0.125")
fig.plot(pltx, vel_resim[STEPS//2].flatten(), lw=2, color='cyan',  label="t=0.25")
fig.plot(pltx, vel_resim[STEPS-1].flatten(),  lw=2, color='purple',label="t=0.5")
#fig.plot(pltx, t0gt, lw=2, color='gray', label="t=0 Reference") # optionally show GT, compare to blue
plt.title("Resimulated u from solution at t=0")
plt.xlabel('x'); plt.ylabel('u'); plt.legend()

注：如果报错np.object was a deprecated...则需要修改：

文件C:\ProgramData\anaconda3\Lib\site-packages\phi\backend\scipy_backend.py第64行

文件C:\ProgramData\anaconda3\Lib\site-packages\phi\struct\struct.py第306行

文件C:\ProgramData\anaconda3\Lib\site-packages\phi\struct\struct.py第315行

修改np.object为np.dtype('O')

下面是 u 在相同时间步长下的 PINN 输出：

velP = [u[0,:,x,0] for x in range(33)]
print(velP[0].shape)

fig = plt.figure().gca()
fig.plot(pltx, velP[BC_TX+ 0].flatten(),       lw=2, color='blue',  label="t=0")
#fig.plot(pltx, velP[BC_TX+STEPS//4].flatten(), lw=2, color='green', label="t=0.125")
fig.plot(pltx, velP[BC_TX+STEPS//2].flatten(), lw=2, color='cyan',  label="t=0.25")
fig.plot(pltx, velP[BC_TX+STEPS-1].flatten(),  lw=2, color='purple',label="t=0.5")
plt.title("NN Output")
plt.xlabel('x'); plt.ylabel('u'); plt.legend()

根据目测标准判断，这两个版本的 $u$ 看起来非常相似，但随着时间的推移，误差会逐渐增大，存在显著差异，这并不奇怪。尤其是在 $x = 0$ 处激波附近解的陡峭化没有被很好地 "捕捉 "到。不过从这两幅图中很难看出来，让我们量化误差，显示实际差异：

error = np.sum( np.abs( np.asarray(vel_resim[0:16]).flatten() - np.asarray(velP[BC_TX:BC_TX+STEPS]).flatten() )) / (STEPS*N)
print("Mean absolute error for re-simulation across {} steps: {:7.5f}".format(STEPS,error))

fig = plt.figure().gca()
fig.plot(pltx, (vel_resim[0       ].flatten()-velP[BC_TX         ].flatten()), lw=2, color='blue',  label="t=5")
fig.plot(pltx, (vel_resim[STEPS//4].flatten()-velP[BC_TX+STEPS//4].flatten()), lw=2, color='green', label="t=0.625")
fig.plot(pltx, (vel_resim[STEPS//2].flatten()-velP[BC_TX+STEPS//2].flatten()), lw=2, color='cyan',  label="t=0.75")
fig.plot(pltx, (vel_resim[STEPS-1 ].flatten()-velP[BC_TX+STEPS-1 ].flatten()), lw=2, color='purple',label="t=1")
plt.title("u Error")
plt.xlabel('x'); plt.ylabel('MAE'); plt.legend()

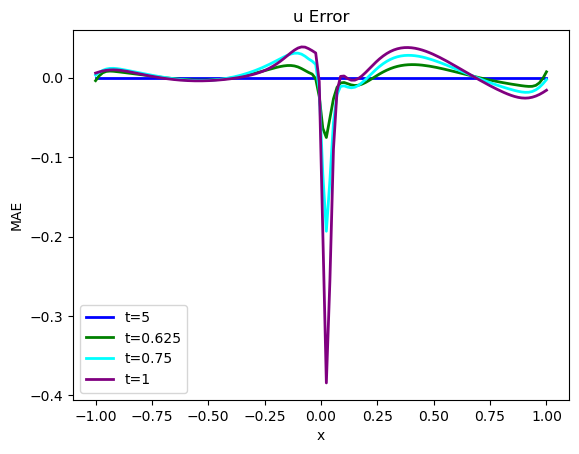
上述代码将计算出地面实况再模拟与 PINN 演化之间的平均绝对误差约为 $1.5 \cdot 1 0^{- 2}$ ，这对于模拟的数值范围而言意义重大。为了与正向模拟和后续案例进行比较，这里还提供了所有随时间变化的步骤，并配有彩色地图。

# show re-simulated solution again as full image over time
sn = np.concatenate(vel_resim, axis=-1)
sn = np.reshape(sn, list(sn.shape)+[1] ) # print(sn.shape)
show_state(sn,"Re-simulated u")

接下来，我们将存储 $t = 0 \dots 1$ 时间间隔内的完整解，以便稍后将其与常规正向求解的完整解进行比较，并与微分物理解进行比较。因此，请继续关注完整的评估和比较。这将在Burgers Optimization with a Differentiable Physics Gradient中，在我们讨论完如何运行微分物理优化的细节之后进行。

vels = session.run(grid_u) # special for showing NN results, run through TF 
vels = np.reshape( vels, [vels.shape[1],vels.shape[2]] )

# save for comparison with other methods
import os; os.makedirs("./temp",exist_ok=True)
np.savez_compressed("./temp/burgers-pinn-solution.npz",vels) ; print("Vels array shape: "+format(vels.shape))

结果为：

Vels array shape: (128, 33)

5.5 后续步骤

当然，这种设置只是 PINN 和物理软约束的一个起点。设置参数的选择是为了相对快速地运行。正如我们在接下来的章节中所展示的，通过将求解器和学习更紧密地结合在一起，这种逆求解的性能可以得到大幅提升。

不过，上述 PINN 设置的解也可以直接加以改进。例如，可以尝试：

调整训练参数，以进一步减少误差，同时不使解发散。
调整 NN 架构以进一步改进（但要跟踪权重计数）。
激活不同的优化器，并观察其行为变化（这通常需要调整学习率）。请注意，在这个相对简单的例子中，更复杂的优化器并不一定做得更好。
或者修改设置，使测试案例更有趣：例如，将边界条件移到模拟时间的较后一点，使重建的时间间隔更大。