前几节中的有监督设置可以通过相当简单的训练过程快速获得近似解。然而，令人痛心的是，我们只是将物理模型和数值方法作为一种 "外部 "工具，来产生一大堆数据。我们人类拥有大量关于如何用数学方法描述物理过程的知识。正如以下几章所展示的，我们可以通过人类的物理知识来指导训练过程，从而改进训练过程。

4.1 使用物理模型

给定一个具有时间演化的 $\mathbf{u}(\mathbf{x},t)$ 的 PDE，我们通常可以用 $\mathcal{F}$ 的导数函数来表示，方法是 $${\mathbf{u}}_t=\mathcal{F}({\mathbf{u}}_x,{\mathbf{u}}_{xx},...{\mathbf{u}}_{xx...x}),$$

其中 $\mathbf{x}$ 的下标表示相对于一个空间维度的高阶空间导数（当然也可以包括相对于不同坐标轴的混合导数）。${\mathbf{u}}_t$ 表示随时间的变化。

在这种情况下，我们可以用神经网络来近似未知的 $\mathbf{u}$ 本身。如果近似值（我们称之为 $\tilde{\mathbf{u}}$ )是准确的，那么 PDE 应该自然满足。换句话说，残差 R 应该等于零： $$R={\mathbf{u}}_t-\mathcal{F}({\mathbf{u}}_x,{\mathbf{u}}_{xx},...{\mathbf{u}}_{xx...x})=0.$$

这与训练神经网络的目标很好地结合在一起：我们可以结合直接损失项来训练最小化残差。与之前类似，除了残差项之外，我们还可以使用预先计算出的解 $[x_0,y_0],...[x_n,y_n]$，将 $\mathbf{u}$ 与 $\mathbf{u}(\mathbf{x})=y$ 作为约束条件。这一点通常很重要，因为除非指定初始条件和边界条件，否则大多数实际的 PDE 都没有唯一解。因此，如果我们只考虑 $R$，可能会得到带有随机偏移或其他不理想成分的解。因此，监督采样点有助于在某些地方固定解。

现在我们的训练目标变成了：

$${\text{arg min}}_{\theta }\sum _i{\alpha }_0(f(x_i;\theta )-y_i^{\ast }{)}^2+{\alpha }_{1}R(x_i)，$$ 其中，${\alpha }_{0,1}$ 表示超参数，分别缩放监督项和残差项的贡献。当然，我们还可以在此添加适当比例系数的附加残差项。

注意方程(1)中两个不同项的含义很有启发：第一项是传统的、有监督的 L2 损失。如果我们只对这一损失进行优化，我们的网络就能很好地学习近似训练样本，但可能会在解中平均出多种模式，在样本点之间的区域表现不佳。相反，如果我们只优化第二项（物理残差），我们的神经网络可能会在局部满足 PDE，但产生的解仍可能与训练数据相去甚远。出现这种情况的原因可能是解中存在 "空位"，即不同的解均满足残差。因此，我们要同时优化这两个目标，以便在最佳情况下，网络在学习近似训练数据的特定解的同时，还能捕捉到底层 PDE 的知识。

需要注意的是，与用于监督训练的数据样本类似，我们无法保证残差项 $R$ 在训练过程中实际为零。训练过程的非线性优化将尽可能减少监督项和残差项，但这并不能保证。仍有可能存在大量非零残差项。我们将在接下来的代码示例中更详细地讨论这个问题，现在重要的是要记住，这种方式的物理约束只代表_软约束_，并不能保证最大限度地减少这些约束。

前面的概述并没有明确说明神经网络是如何产生 $\mathbf{u}$ 的。在这里，我们可以区分两种不同的方法：通过选择目标函数的显式表示（下文中的 v1），或通过使用全连接神经网络来表示解（v2）。例如，对于 v1，我们可以设置一个空间网格（或图形，或一组样本点），而在第二种情况下，不存在显式表示，而是由神经网络接收空间坐标，在查询位置生成解。下面我们将详细介绍这两种变体。

4.2 变体 1: 用于显式表示的残差导数

对于变式 1，我们选择离散化，并建立一个覆盖目标域的计算网格。在不失一般性的前提下，我们假设这是一个笛卡尔网格，以 $\mathbf{p}$ 的位置对空间进行采样。现在，训练一个 NN 来生成网格上的解：$\mathbf{u}(\mathbf{p})=f(\mathbf{x};\theta )$。对于规则网格，CNN 将是 $f$ 的最佳选择，而对于三角形网格，我们可以使用图网络，或使用点演算的粒子网络。

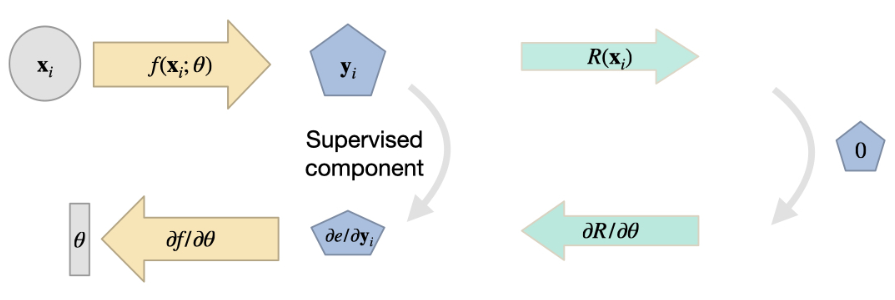
现在，我们可以在计算网格上将 $R$ 的方程离散化，并用我们选择的方法计算导数。唯一需要注意的是：为了将残差纳入训练，我们必须制定评估方法，使深度学习框架可以通过计算进行反向传播。由于我们的网络 $f()$ 产生了解 $\mathbf{u}$，而残差取决于它（$R(\mathbf{u})$），因此我们至少需要 $\partial R/\partial \mathbf{u}$，这样才能对权重 $\theta$ 进行梯度反向传播。幸运的是，如果我们用 DL 框架的操作来表示 $R$，那么该框架的反向传播功能就能解决这个问题。

这种变体在DL中有着相当悠久的 "传统"，例如，Tompson et al. [TSSP17]很早就提出了这种变体来学习无散度运动。举个具体例子：如果我们的目标是学习无散度的速度 $\mathbf{u}(t)$，我们就可以使用这种训练方法来训练 NN，而无需预先计算无发散速度场作为训练数据。为了简洁起见，我们在这里将去掉空间指数（$\mathbf{p}$），并将重点放在$t$上，我们同样可以将其简化：无散度必须在任何时候都保持不变，因此我们可以考虑从$t=0$开始的单一步骤，即从有散度的$\mathbf{u}(0)$到无散度的$\mathbf{u}(1)$的归一化步骤。对于正常求解器，我们必须计算一个压力 $p={\nabla }^{-2}\mathbf{u}(0)$，使得 $\mathbf{u}(1)=\mathbf{u}(0)-\nabla p$。这就是著名的矢量微积分基本定理，或Helmholtz decomposition，把矢量场分成_solenoidal_（无散度）和非旋转部分（压力梯度）。

为了学习这种分解，我们可以在计算网格上用 CNN 近似计算 $p$：$p=f(\mathbf{u}(0);\theta )$。学习目标变成最小化 $\mathbf{u}(0)$ 的发散，也就是最小化 $\nabla \cdot (\mathbf{u}(0)-\nabla f(\mathbf{u}(0);\theta ))$ 。为了实现这个残差，我们只需在计算网格上提供 $\mathbf{u}$ 的发散算子 $(\nabla \cdot )$ 即可。这通常可以通过 DL 框架中的卷积层轻松实现，该卷积层包含发散的有限差分权重。非常好的是，在这种情况下，我们甚至不需要额外的监督样本，通常只需使用这种残差公式进行训练即可。另外，与下面的变式 2 不同，我们可以直接处理相当大的解空间（我们并不局限于学习单个解）。我们可以在 代码库 中找到一个实现示例。

总的来说，变式 1 与可微分物理训练有很多共同之处（它基本上是一个子集）。由于我们将在 Introduction to Differentiable Physics和之后的文章中更详细地讨论可微分物理，从现在起，我们将专注于直接 NN 表示（变体 2）。

4.3 变体 2: 来自神经网络表示的导数

采用物理残差作为软约束的第二种变体是使用全连接的 NN 来表示 $\mathbf{u}$。这种_physics-infformed_方法由 Raissi 等人推广[RPK19]，它有一些有趣的优点和缺点，我们将在下文中概述。在下面的代码示例和讨论中，我们将以物理信息版本（变体 2）为目标。

这里的中心思想是，我们在学习问题中所追求的上述通用函数 $f$ 也可以用来获得物理场的表示，例如，满足 $R=0$ 的场 $\mathbf{u}$。这意味着 $\mathbf{u}(\mathbf{x})$ 将转化为 $\mathbf{u}(\mathbf{x},\theta )$，其中我们选择的 NN 参数 $\theta$ 可以尽可能精确地表示出所需的 $\mathbf{u}$。

这种观点的一个很好的副作用是，NN 表征本质上支持导数的计算。导数 $\partial f/\partial \theta$ 是通过梯度下降进行学习的关键基石，这在 Overview 中已有解释。现在，我们可以用同样的工具来计算空间导数，比如 $\partial \mathbf{u}/\partial x$，注意，上面对于 $R$，我们把这个导数写成了简写符号 ${\mathbf{u}}_x$。对于随时间变化的函数，这当然也适用于 $\partial \mathbf{u}/\partial t$，即上面符号中的 ${\mathbf{u}}_t$ 。

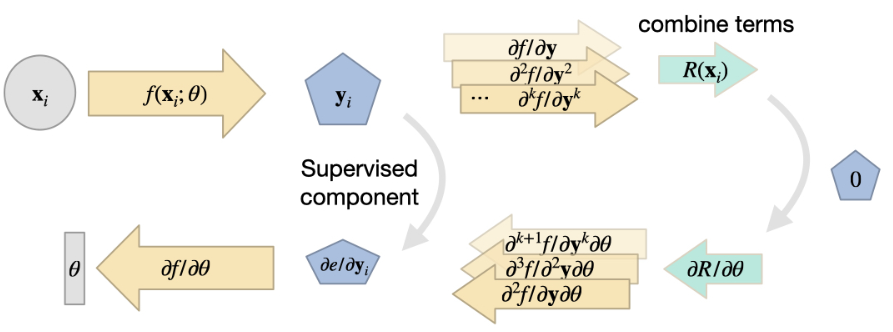
因此，对于由${\mathbf{u}}_t$和${\mathbf{u}}_x$项组成的通用$R$，一旦我们有了代表$\mathbf{u}$的NN，我们就可以依靠DL框架的反向传播算法来计算这些导数。从本质上讲，这给我们提供了一个函数（NN），该函数接收空间和时间坐标来生成 $\mathbf{u}$ 的解。因此，输入通常是相当低维的，例如三维情况下随时间变化的 3+1 个值，通常会产生一个标量值或空间向量。由于缺乏明确的空间采样点，这里选择了 MLP（即全连接 NN）架构。

举个简单的例子，一维Burgers方程， $\frac{\partial u}{\partial t}+u\nabla u=\nu \nabla \cdot \nabla u$ ，我们可以直接提出一个损失项 $R=\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}-\nu \frac{{\partial }^{2}u}{\partial x^2}$，在训练时应尽可能将其最小化。对于每个项，例如 $\frac{\partial u}{\partial x}$，我们可以简单地查询实现 $u$ 的 DL 框架，以获得相应的导数。对于高阶导数，例如 $\frac{{\partial }^{2}u}{\partial x^2}$，我们可以简单地多次查询框架的导函数。在下一节中，我们将举例说明如何在 tensorflow 中实现这一功能。

4.4 到目前为止的总结

上述方法为我们提供了一种将物理方程作为软约束纳入 DL 学习的方法：残差损失。通常情况下，这种设置适用于逆问题，即我们想要找到一个 PDE 解的某些测量或观测结果。由于重构的成本很高（将在下文中演示），解流形不应该过于复杂。例如，仅使用物理残余损失通常无法捕捉到广泛的解，如之前的监督机翼示例。