这里的监督（Supervised）主要是指："用老办法做事"。当然，在深度学习（DL）的语境中，"老套"还是相当新的。此外，"老套"并不总是意味着不好--我们稍后将讨论训练网络的方法，这些方法明显优于使用监督训练的方法。

尽管如此，"监督训练 "是人们在 DL 背景下遇到的所有项目的起点，因此值得研究。此外，虽然 "监督训练 "的结果通常不如基于物理学的方法，但在某些应用场景中，如果没有好的模型方程，"监督训练 "可能是唯一的选择。

3.1 问题设置

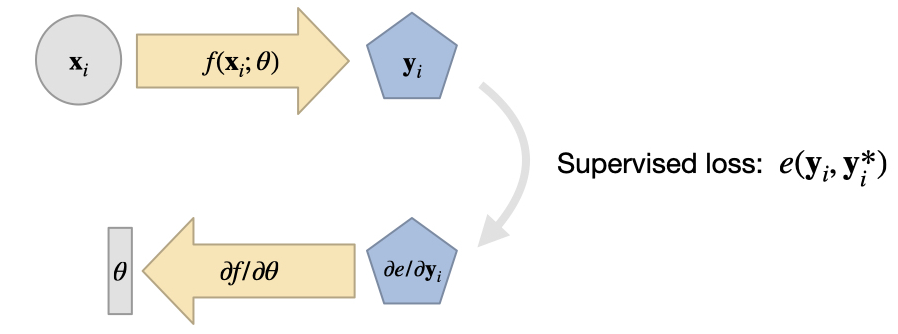
在监督训练中，我们面对一个未知函数 $f^{*} (x) = y^{*}$ ，收集大量数据对 $[x_{0}, y_{0}^{*}] ， ... [x_{n}, y_{n}^{*}]$ （训练数据集），并直接训练一个 NN 来表示 $f^{*}$ 的近似值 $f$ 。

我们用这种方法得到的 $f$ 通常不是精确的，而是通过最小化问题得到的：通过调整表示 $f$ 的 NN 的权重 $θ$ ，使得 $arg min_{θ} i \sum (f (x_{i}; θ) - y_{i}^{*})^{2} .$

这样我们就能得到 $θ$ ，从而在我们选择 $f$ 和超参数进行训练的情况下，尽可能精确地得到 $f (x; θ) = y \approx y^{*}$ 的结果。请注意，上面我们假设的是最简单的 $L^{2}$ 损失。更一般的版本会在损失 $L$ 中使用一个误差度量 $e (x, y)$ ，通过 $arg min_{θ} \sum_{i} e (f (x_{i}; θ), y_{i}^{*}))$ 来最小化。关于合适度量的选择，我们稍后再讨论。

无论我们选择哪种度量方法，这一表述都给出了监督式方法的实际 "学习 "过程。

训练数据通常需要相当大的规模，因此使用数值模拟求解物理模型 $P$ 来产生大量可靠的输入输出对进行训练是很有吸引力的。这意味着训练过程使用一组模型方程，并对其进行数值近似，以训练 NN 表示 $f$ 。这样做有很多好处，例如，我们没有真实世界设备的测量噪声，也不需要人工标注大量样本来获取训练数据。

另一方面，这种方法也继承了以模拟代替实验的常见挑战：首先，我们需要确保所选模型有足够的能力来预测我们感兴趣的真实世界现象的行为。此外，数值近似会产生数值误差，需要将误差控制得足够小，以满足所选应用的需要。由于这些问题在经典模拟中都有深入研究，因此同样可以利用现有知识来设置 DL 训练任务。

3.2 代理模型

上述监督方法的核心优势之一是我们可以得到一个 代理模型(Surrogate Model)，即一个模仿原始 $P$ 行为的新函数。针对现实世界现象的 PDE 模型的数值近似通常计算成本很高。另一方面，训练有素的 NN 每次评估的成本是固定的，而且在 GPU 或 NN 单元等专用硬件上进行评估通常是微不足道的。

尽管如此，还是要小心谨慎：神经网络可以迅速产生大量介于两者之间的结果。考虑一个具有 $128$ 特征的 CNN 层。如果我们将其应用于 $12 8^{2}$ 的输入，即大约 16k 个单元，我们会得到 $12 8^{3}$ 的中间值。这就超过了 200 万。所有这些值至少需要暂时存储在内存中，并由下一层进行处理。

尽管如此，我们仍需谨慎: NN 可以快速生成大量中间结果。考虑一个具有 $128$ 个特征的 CNN 层。如果我们将其应用于 $12 8^{2}$ ，即大约 16 k 个单元的输入，我们会得到 $12 8^{3}$ 个中间值。这已经超过了 200 万。这些值至少需要暂时存储在内存中，并由下一层处理。

然而，用快速、可学习的近似方法取代复杂、昂贵的求解器是一个非常有吸引力和有趣的方向。

3.3 给我看看代码!

最后，让我们来看一个训练神经网络的代码示例：我们将用[TWPH20]中的代用模型替换机翼周围湍流的完整求解器。

3.4 翼型周围 RANS 流动的监督训练

3.4.1 概述

在这个监督训练的例子中，我们有一个翼面周围的湍流气流，我们想知道在不同雷诺数和攻角下，该翼面周围的平均运动和压力分布。因此，在给定机翼形状、雷诺数和攻角的情况下，我们希望获得机翼周围的速度场和压力场。

经典的近似方法是_雷诺兹平均纳维-斯托克斯（RANS）模型，这种设置仍然是纳维-斯托克斯求解器在工业中最广泛的应用之一。不过，我们现在的目标不是依靠传统的数值方法来求解 RANS 方程，而是通过神经网络训练一个完全绕过数值求解器的代理模型，并以速度和压力的形式求解。

run in colab

3.4.2 准备工作

根据监督模型的描述，我们的学习任务非常简单直接，可以写成

$arg min_{θ} i \sum (f (x_{i}; θ) - y_{i}^{*})^{2} ，$ 其中， $x$ 和 $y^{*}$ 分别由一组物理场组成，而索引 $i$ 则表示数据集所有离散点的差值。

我们的目标是在围绕翼面的计算域 $Ω$ 中推断速度 $u = u_{x}, u_{y}$ 和压力场 $p$ 。作为输入，我们有雷诺数 $Re$ 。在 $R$ 中的雷诺数 $Re$ 、攻角 $α \in R$ 中的攻角 $α$ ，以及机翼形状 $s$ ，这些数据以 $12 8^{2}$ 的栅格编码。 $Re$ 和 $α$ 是以自由流流速 $f$ 的形式提供的，其 x 和 y 分量表示为相同大小的常数域，在机翼区域包含零。因此，输入和输出具有相同的尺寸： $x, y^{*} \in R^{3 \times 128 \times 128}$ 。输入包含 $[f_{x}, f_{y}, mask]$ ，而输出则存储通道 $[p, u_{x}, u_{y}]$ 。这正是我们下面要为 NN 指定的输入和输出维度。

这里需要注意的一点是，我们在 $y^{*}$ 中关注的量包含三个不同的物理场。虽然两个速度分量在本质上非常相似，但压力场通常具有与速度近似平方缩放的不同行为（参见伯努利）。这意味着我们需要小心处理简单求和（如上文的最小化问题），并注意对数据进行归一化处理。

3.4.3 代码即将出现...

让我们开始实施吧。请注意，我们将跳过数据生成过程。下面的代码改变this codebase。在这里，我们只需下载一小部分在OpenFOAM中通过 Spalart-Almaras RANS 仿真生成的训练数据。

import numpy as np
import os.path, random
import torch
from torch.utils.data import Dataset
print("Torch version {}".format(torch.__version__))

# get training data
dir = "./"
if True:
    # download
    if not os.path.isfile('data-airfoils.npz'):
        import requests
        print("Downloading training data (300MB), this can take a few minutes the first time...")
        with open("data-airfoils.npz", 'wb') as datafile:
            resp = requests.get('https://dataserv.ub.tum.de/s/m1615239/download?path=%2F&files=dfp-data-400.npz', verify=False)
            datafile.write(resp.content)
else: 
    # alternative: load from google drive (upload there beforehand):
    from google.colab import drive
    drive.mount('/content/gdrive')
    dir = "./gdrive/My Drive/"

npfile=np.load(dir+'data-airfoils.npz')    
print("Loaded data, {} training, {} validation samples".format(len(npfile["inputs"]),len(npfile["vinputs"])))
print("Size of the inputs array: "+format(npfile["inputs"].shape))

Torch version 2.0.1+cu118
Downloading training data (300MB), this can take a few minutes the first time...
Loaded data, 320 training, 80 validation samples
Size of the inputs array: (320, 3, 128, 128)

如果您在 colab 中运行本笔记本，上面的 else语句（默认情况下未激活）可能会对您有帮助：与其每次都重新下载训练数据，您可以手动下载一次并将其存储在谷歌硬盘中。我们假设它存储在根目录下，名为 data-airfoils.npz。之后，您可以使用上面的代码从谷歌硬盘加载文件，这样通常会快很多。如果您想通过 colab 进行更广泛的实验，强烈建议使用此方法。

3.4.4 RANS 训练数据

现在我们有了一些训练数据。一般来说，尽可能多地了解我们正在使用的数据是非常重要的（对于任何 ML 任务来说，garbage-in-gargabe-out 原则绝对成立）。我们至少应该从维度和粗略统计的角度来理解数据，最好还能从内容的角度来理解数据。否则，我们将很难解释训练运行的结果。而且，尽管有所有的 DL 魔法：如果你无法在数据中找出任何模式，NNs 肯定也找不到任何有用的模式。

因此，让我们来看看其中一个训练样本...下面只是一些辅助代码，用于并排显示图像。

import pylab

# helper to show three target channels: normalized, with colormap, side by side
def showSbs(a1,a2, stats=False, bottom="NN Output", top="Reference", title=None): 
  c=[]
  for i in range(3):
    b = np.flipud( np.concatenate((a2[i],a1[i]),axis=1).transpose())
    min, mean, max = np.min(b), np.mean(b), np.max(b); 
    if stats: print("Stats %d: "%i + format([min,mean,max]))
    b -= min; b /= (max-min)
    c.append(b)
  fig, axes = pylab.subplots(1, 1, figsize=(16, 5))
  axes.set_xticks([]); axes.set_yticks([]); 
  im = axes.imshow(np.concatenate(c,axis=1), origin='upper', cmap='magma')

  pylab.colorbar(im); pylab.xlabel('p, ux, uy'); pylab.ylabel('%s           %s'%(bottom,top))
  if title is not None: pylab.title(title)

NUM=72
showSbs(npfile["inputs"][NUM],npfile["targets"][NUM], stats=False, bottom="Target Output", top="Inputs", title="3 inputs are shown at the top (free-ux, free-uy, mask), with the 3 output channels (p,ux,uy) at the bottom")

接下来，让我们定义一个小的辅助类 DfpDataset 来组织输入和目标。我们将把相应的数据传输到 pytorch 的 DataLoader类。

我们还设置了一些全局参数来控制训练参数，其中最重要的可能是：学习率 LR，即从上一次训练中获得的 $η$ 。当训练运行没有收敛时，这是第一个需要实验的参数。

在这里，我们将始终保持相对较小的学习率。(使用学习率衰减会更好，即有可能改善收敛性，但为了清晰起见，此处省略）。

# some global training constants

# number of training epochs
EPOCHS = 100
# batch size
BATCH_SIZE = 10
# learning rate
LR = 0.00002

class DfpDataset():
    def __init__(self, inputs,targets): 
        self.inputs  = inputs
        self.targets = targets

    def __len__(self):
        return len(self.inputs)

    def __getitem__(self, idx):
        return self.inputs[idx], self.targets[idx]

tdata = DfpDataset(npfile["inputs"],npfile["targets"])
vdata = DfpDataset(npfile["vinputs"],npfile["vtargets"])

trainLoader = torch.utils.data.DataLoader(tdata, batch_size=BATCH_SIZE, shuffle=True , drop_last=True) 
valiLoader  = torch.utils.data.DataLoader(vdata, batch_size=BATCH_SIZE, shuffle=False, drop_last=True) 

print("Training & validation batches: {} , {}".format(len(trainLoader),len(valiLoader) ))

输出结果为：

Training & validation batches: 32 , 8

3.4.5 网络设置

现在我们可以设置神经网络的架构，我们将使用完全卷积 U-net。这是一种广泛使用的架构，使用不同空间分辨率的卷积堆叠。与普通卷积网络的主要区别在于，从编码器到解码器部分引入了skip connection。这可以确保在特征提取过程中不会丢失任何信息。(请注意，这只有在网络作为一个整体使用时才有效。例如，如果我们想将解码器作为一个独立的组件来使用，这就行不通了）。

下面是体系结构概述:

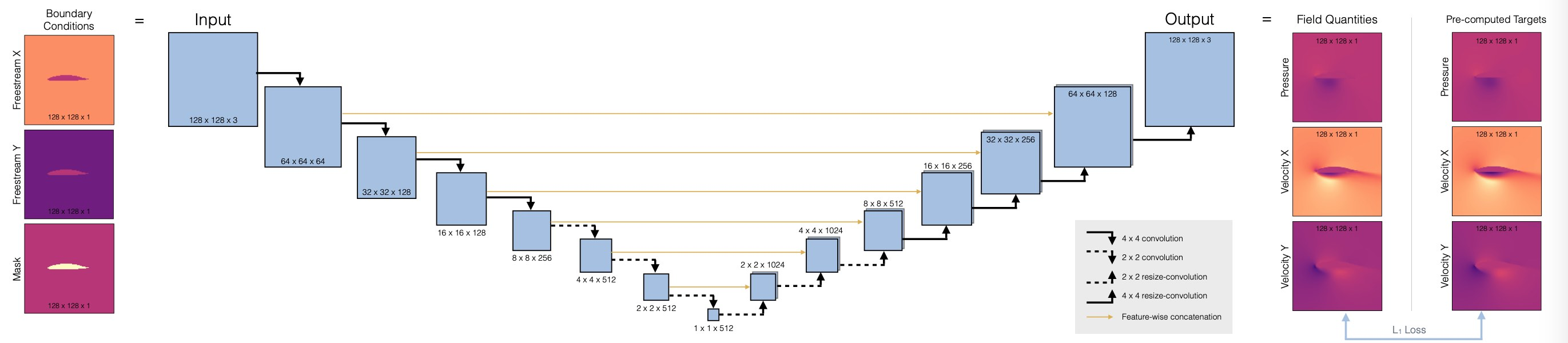
首先，我们将定义一个辅助程序，用于在网络中设置一个卷积块，即 blockUNet 。注意，我们不使用任何池化！相反，我们按照最佳实践，使用跨距和转置卷积（解码器部分需要对称，即内核大小不均）。完整的 pytroch 神经网络通过 DfpNet 类进行管理。

import os, sys, random
import numpy as np

import torch
import torch.nn as nn
import torch.optim as optim
import torch.autograd 
import torch.utils.data 

def blockUNet(in_c, out_c, name, size=4, pad=1, transposed=False, bn=True, activation=True, relu=True, dropout=0. ):
    block = nn.Sequential()

    if not transposed:
        block.add_module('%s_conv' % name, nn.Conv2d(in_c, out_c, kernel_size=size, stride=2, padding=pad, bias=True))
    else:
        block.add_module('%s_upsam' % name, nn.Upsample(scale_factor=2, mode='bilinear'))
        # reduce kernel size by one for the upsampling (ie decoder part)
        block.add_module('%s_tconv' % name, nn.Conv2d(in_c, out_c, kernel_size=(size-1), stride=1, padding=pad, bias=True))

    if bn:
        block.add_module('%s_bn' % name, nn.BatchNorm2d(out_c))
    if dropout>0.:
        block.add_module('%s_dropout' % name, nn.Dropout2d( dropout, inplace=True))

    if activation:
        if relu:
            block.add_module('%s_relu' % name, nn.ReLU(inplace=True))
        else:
            block.add_module('%s_leakyrelu' % name, nn.LeakyReLU(0.2, inplace=True))

    return block
    
class DfpNet(nn.Module):
    def __init__(self, channelExponent=6, dropout=0.):
        super(DfpNet, self).__init__()
        channels = int(2 ** channelExponent + 0.5)

        self.layer1 = blockUNet(3         , channels*1, 'enc_layer1', transposed=False, bn=True, relu=False, dropout=dropout )
        self.layer2 = blockUNet(channels  , channels*2, 'enc_layer2', transposed=False, bn=True, relu=False, dropout=dropout )
        self.layer3 = blockUNet(channels*2, channels*2, 'enc_layer3', transposed=False, bn=True, relu=False, dropout=dropout )
        self.layer4 = blockUNet(channels*2, channels*4, 'enc_layer4', transposed=False, bn=True, relu=False, dropout=dropout )
        self.layer5 = blockUNet(channels*4, channels*8, 'enc_layer5', transposed=False, bn=True, relu=False, dropout=dropout ) 
        self.layer6 = blockUNet(channels*8, channels*8, 'enc_layer6', transposed=False, bn=True, relu=False, dropout=dropout , size=2,pad=0)
        self.layer7 = blockUNet(channels*8, channels*8, 'enc_layer7', transposed=False, bn=True, relu=False, dropout=dropout , size=2,pad=0)
     
        # note, kernel size is internally reduced by one for the decoder part
        self.dlayer7 = blockUNet(channels*8, channels*8, 'dec_layer7', transposed=True, bn=True, relu=True, dropout=dropout , size=2,pad=0)
        self.dlayer6 = blockUNet(channels*16,channels*8, 'dec_layer6', transposed=True, bn=True, relu=True, dropout=dropout , size=2,pad=0)
        self.dlayer5 = blockUNet(channels*16,channels*4, 'dec_layer5', transposed=True, bn=True, relu=True, dropout=dropout ) 
        self.dlayer4 = blockUNet(channels*8, channels*2, 'dec_layer4', transposed=True, bn=True, relu=True, dropout=dropout )
        self.dlayer3 = blockUNet(channels*4, channels*2, 'dec_layer3', transposed=True, bn=True, relu=True, dropout=dropout )
        self.dlayer2 = blockUNet(channels*4, channels  , 'dec_layer2', transposed=True, bn=True, relu=True, dropout=dropout )
        self.dlayer1 = blockUNet(channels*2, 3         , 'dec_layer1', transposed=True, bn=False, activation=False, dropout=dropout )

    def forward(self, x):
        # note, this Unet stack could be allocated with a loop, of course... 
        out1 = self.layer1(x)
        out2 = self.layer2(out1)
        out3 = self.layer3(out2)
        out4 = self.layer4(out3)
        out5 = self.layer5(out4)
        out6 = self.layer6(out5)
        out7 = self.layer7(out6)
        # ... bottleneck ...
        dout6 = self.dlayer7(out7)
        dout6_out6 = torch.cat([dout6, out6], 1)
        dout6 = self.dlayer6(dout6_out6)
        dout6_out5 = torch.cat([dout6, out5], 1)
        dout5 = self.dlayer5(dout6_out5)
        dout5_out4 = torch.cat([dout5, out4], 1)
        dout4 = self.dlayer4(dout5_out4)
        dout4_out3 = torch.cat([dout4, out3], 1)
        dout3 = self.dlayer3(dout4_out3)
        dout3_out2 = torch.cat([dout3, out2], 1)
        dout2 = self.dlayer2(dout3_out2)
        dout2_out1 = torch.cat([dout2, out1], 1)
        dout1 = self.dlayer1(dout2_out1)
        return dout1

def weights_init(m):
    classname = m.__class__.__name__
    if classname.find('Conv') != -1:
        m.weight.data.normal_(0.0, 0.02)
    elif classname.find('BatchNorm') != -1:
        m.weight.data.normal_(1.0, 0.02)
        m.bias.data.fill_(0)

接下来，我们可以初始化一个 DfpNet实例。

下面，EXPO参数控制着我们的 Unet 特征图的指数：这直接决定了网络的大小（3 可以使网络拥有约 15 万个参数）。这对于一个有 $3 \times 12 8^{2} = ca. 49 k$ 输出的生成式 NN 而言，这个参数相对较小，但训练时间很快，而且可以防止过度拟合，因为我们在这里使用的数据集相对较小。因此，这是一个很好的起点。

# channel exponent to control network size
EXPO = 3

# setup network
net = DfpNet(channelExponent=EXPO)
#print(net) # to double check the details...

nn_parameters = filter(lambda p: p.requires_grad, net.parameters())
params = sum([np.prod(p.size()) for p in nn_parameters])

# crucial parameter to keep in view: how many parameters do we have?
print("Trainable params: {}   -> crucial! always keep in view... ".format(params)) 

net.apply(weights_init)

criterionL1 = nn.L1Loss()
optimizerG = optim.Adam(net.parameters(), lr=LR, betas=(0.5, 0.999), weight_decay=0.0)

targets = torch.autograd.Variable(torch.FloatTensor(BATCH_SIZE, 3, 128, 128))
inputs  = torch.autograd.Variable(torch.FloatTensor(BATCH_SIZE, 3, 128, 128))

Trainable params: 147363   -> crucial! always keep in view...

指数为 3 时，该网络有 147555 个可训练参数。正如打印语句中的微妙提示所示，在训练 NN 时，这是一个需要时刻关注的关键数字。改变设置很容易得到一个拥有数百万个参数的网络，结果可能会出现各种收敛和过拟合问题。参数的数量肯定要与训练数据的数量相匹配，还应该与网络的深度成比例。不过，这三者之间的确切关系取决于问题的具体情况。

3.4.6 训练

最后，我们可以对 NN 进行训练。这一步可能要花费一些时间，因为训练会对所有 320 个样本运行 100 次，并不断评估验证样本，以跟踪 NN 的当前状态。

history_L1 = []
history_L1val = []

if os.path.isfile("network"):
  print("Found existing network, loading & skipping training")
  net.load_state_dict(torch.load("network")) # optionally, load existing network

else:
  print("Training from scratch")
  for epoch in range(EPOCHS):
      net.train()
      L1_accum = 0.0
      for i, traindata in enumerate(trainLoader, 0):
          inputs_curr, targets_curr = traindata
          inputs.data.copy_(inputs_curr.float())
          targets.data.copy_(targets_curr.float())

          net.zero_grad()
          gen_out = net(inputs)

          lossL1 = criterionL1(gen_out, targets)
          lossL1.backward()
          optimizerG.step()
          L1_accum += lossL1.item()

      # validation
      net.eval()
      L1val_accum = 0.0
      for i, validata in enumerate(valiLoader, 0):
          inputs_curr, targets_curr = validata
          inputs.data.copy_(inputs_curr.float())
          targets.data.copy_(targets_curr.float())

          outputs = net(inputs)
          outputs_curr = outputs.data.cpu().numpy()

          lossL1val = criterionL1(outputs, targets)
          L1val_accum += lossL1val.item()

      # data for graph plotting
      history_L1.append( L1_accum / len(trainLoader) )
      history_L1val.append( L1val_accum / len(valiLoader) )

      if epoch<3 or epoch%20==0:
          print( "Epoch: {}, L1 train: {:7.5f}, L1 vali: {:7.5f}".format(epoch, history_L1[-1], history_L1val[-1]) )

  torch.save(net.state_dict(), "network" )
  print("Training done, saved network")

程序输出结果为：

Training from scratch
Epoch: 0, L1 train: 0.29219, L1 vali: 0.23295
Epoch: 1, L1 train: 0.25406, L1 vali: 0.22507
Epoch: 2, L1 train: 0.22487, L1 vali: 0.21019
Epoch: 20, L1 train: 0.05228, L1 vali: 0.04134
Epoch: 40, L1 train: 0.03730, L1 vali: 0.03020
Epoch: 60, L1 train: 0.03236, L1 vali: 0.02523
Epoch: 80, L1 train: 0.03364, L1 vali: 0.02302
Training done, saved network

NN 终于训练完成！损失的绝对值应该已经很好地下降了：在标准设置下，验证损失的初始值约为 0.2，100 个epoch后约为 0.02。

让我们看看图表，直观地了解训练是如何随时间推移的。这对于识别训练的长期趋势非常重要。在实践中，很难发现命令行日志中 100 个左右的嘈杂数字的整体趋势是略微上升还是下降，而这在可视化中更容易发现。

import matplotlib.pyplot as plt

l1train = np.asarray(history_L1)
l1vali  = np.asarray(history_L1val)

plt.plot(np.arange(l1train.shape[0]),l1train,'b',label='Training loss')
plt.plot(np.arange(l1vali.shape[0] ),l1vali ,'g',label='Validation loss')
plt.legend()
plt.show()

程序输出如下：

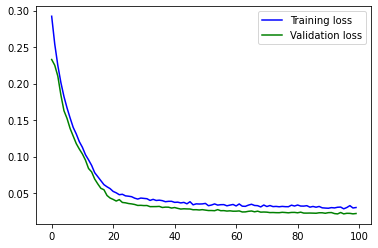
您应该看到一条曲线，它在大约 40 个epoch中一直在下降，然后开始变得平缓。在最后一部分，它仍在缓慢下降，最重要的是，验证损失并没有增加。这肯定是过度拟合的迹象，我们应该避免。(试着人为减少训练数据量，就能有意识地造成过度拟合）。

3.4.7 训练进度和验证

如果仔细观察这张图，你会发现一些奇怪的现象：为什么验证损失低于训练损失？

当然，这些数据与训练数据类似，但从某种程度上说，它们略微 "艰难 "一些，因为网络在训练过程中肯定从未收到过任何验证样本。验证损失略微偏离训练损失是很自然的，但对于这些输入，L1 损失怎么会更低？

这是由于上述训练循环在 pytorch 中的实现方式造成的：虽然训练损失是在训练模式下通过 net.train() 进行评估的，但评估是在调用 net.eval() 之后进行的。这将关闭批量归一化，并禁用 dropout（如果激活）等功能。这会稍微改变评估结果。代码还会运行一个训练步骤，根据网络在一个epoch中的演化状态来测量图中每个点的损失。更新网络后，再运行验证样本。因此，所有验证样本所使用的状态都与历时的初始状态略有不同（希望更好一些）。由于这两个原因，验证损失可能会有偏差，在本例中通常会略低一些。

这里需要提醒的是：永远不要用训练数据来评估你的网络！因为过度拟合是一个非常常见的问题。至少要使用网络从未见过的数据，即验证数据，如果看起来不错，再尝试一些不同的（至少稍微超出分布范围的）输入，即_测试数据_。下一个单元格将在验证数据上运行训练有素的网络，并使用 showSbs 函数显示其中一个数据。

net.eval()
for i, validata in enumerate(valiLoader, 0):
    inputs_curr, targets_curr = validata
    inputs.data.copy_(inputs_curr.float())
    targets.data.copy_(targets_curr.float())
    
    outputs = net(inputs)
    outputs_curr = outputs.data.cpu().numpy()
    if i<1: showSbs(targets_curr[0] , outputs_curr[0], title="Validation sample %d"%(i*BATCH_SIZE))

输出结果为：

从外观上看，输入和网络输出之间至少应该有大致的相似之处。不过，我们还是留待测试数据时再进行更详细的评估吧。

3.4.8 测试评估

现在我们来看看实际的测试样本：在这种情况下，我们将使用新的机翼形状作为分布外（OOD）数据。这些形状是网络在任何训练样本中都从未见过的，因此它可以告诉我们网络对未见输入的泛化程度（验证数据不足以得出泛化结论）。

我们将使用与之前相同的可视化方式，正如伯努利方程所示，尤其是第一列中的_压力_对网络来说是一个具有挑战性的量。由于它与输入自由流速度和局部峰值呈立方比例关系，因此是网络最难推断的量。

下面的单元首先下载包含这些测试数据样本的较小档案，然后通过网络运行。评估循环还会计算累计 L1 误差，这样我们就可以量化网络在测试样本上的表现。

if not os.path.isfile('data-airfoils-test.npz'):
  import urllib.request
  url="https://physicsbaseddeeplearning.org/data/data_test.npz"
  print("Downloading test data, this should be fast...")
  urllib.request.urlretrieve(url, 'data-airfoils-test.npz')

nptfile=np.load('data-airfoils-test.npz')
print("Loaded {}/{} test samples\n".format(len(nptfile["test_inputs"]),len(nptfile["test_targets"])))

testdata = DfpDataset(nptfile["test_inputs"],nptfile["test_targets"])
testLoader  = torch.utils.data.DataLoader(testdata, batch_size=1, shuffle=False, drop_last=True) 

net.eval()
L1t_accum = 0.
for i, validata in enumerate(testLoader, 0):
    inputs_curr, targets_curr = validata
    inputs.data.copy_(inputs_curr.float())
    targets.data.copy_(targets_curr.float())

    outputs = net(inputs)
    outputs_curr = outputs.data.cpu().numpy()

    lossL1t = criterionL1(outputs, targets)
    L1t_accum += lossL1t.item()
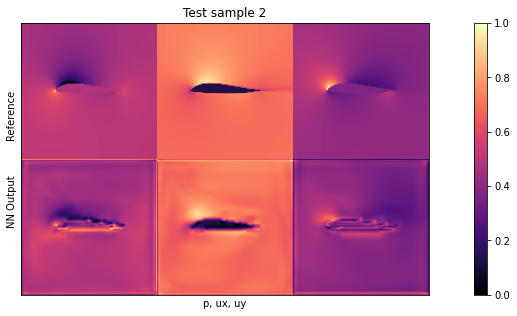
    if i<3: showSbs(targets_curr[0] , outputs_curr[0],  title="Test sample %d"%(i))

print("\nAverage test error: {}".format( L1t_accum/len(testLoader) ))

Downloading test data, this should be fast...
Loaded 10/10 test samples
Average test error: 0.028802116494625808

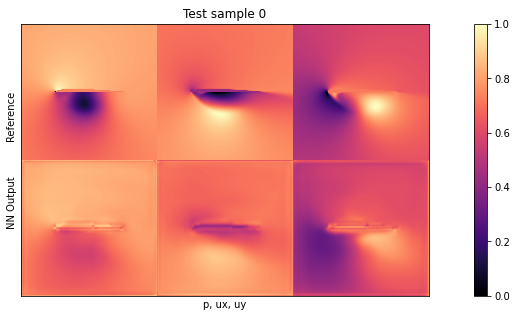
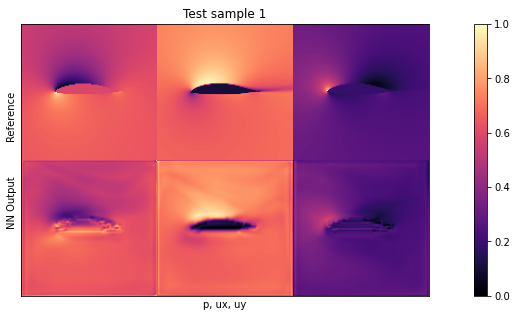
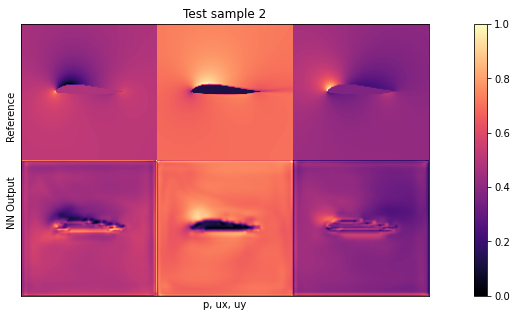
默认设置下的平均测试误差应约为 0.03。由于输入已归一化，这意味着所有三个字段的平均误差为每个量的最大值的 3%。这对于新形状来说不算太差，但显然还有改进的余地。

通过观察可视化效果，您会发现输出结果中缺少特别高的压力峰值和较大的 yvelocities 小区。这主要是由于网络太小，没有足够的资源来重建细节。

尽管如此，我们还是成功地用一个非常小而快速的神经网络架构取代了相当复杂的 RANS 求解器。它 "开箱即用"（通过 pytorch），支持 GPU，可微分，引入的误差仅为百分之几。通过额外的改动和更多的数据，这个设置可以变得非常精确[CT21]。

3.4.9 下一步

有很多显而易见的方法可以尝试（见下面的建议），例如延长训练时间、扩大数据集、扩大网络规模等。

试验学习率、辍学率和网络规模，以减少测试集上的误差。在给定训练数据的情况下，你能把误差减到多小？
述设置使用的是归一化数据。相反，你可以恢复撤销归一化后的原始场来检查网络在原始数量上的表现。
正如你所看到的，在这里你能从这个数据集得到的东西有点有限，你可以去这个项目的主 github 仓库下载更大的数据集，或者生成自己的数据。

3.5 监督方法讨论

前面的例子说明，我们可以很容易地使用监督训练来解决复杂的任务。主要的工作量是收集足够大的示例数据集。一旦有了这些数据集，我们就可以训练一个网络来近似这些解法采样的解流形，训练好的网络可以很快给出预测结果。在使用监督训练时，有几个要点需要注意。

3.5.1 一些需要注意的事项...

3.5.1.1 自然出发点

监督训练是任何 DL项目的自然起点。在这里，我们的意思是总是，从使用尽可能少的数据进行完全监督测试开始是有意义的。这将是一个纯粹的过拟合测试，但如果你的网络不能快速收敛并在单个示例上提供非常好的性能，那么你的代码或数据就存在根本性的问题。因此，我们没有理由继续进行更复杂的设置，因为这会增加发现这些基本问题的难度。

总结前几节的零散评论，这里有一套建立 DL 项目的 "黄金法则"：

始终从 1 个样本的过拟合测试开始。- 检查网络有多少可训练参数。
缓慢增加训练数据量（以及可能的网络参数和深度）。
调整超参数（尤其是学习率）。
然后引入其他组件，如可变求解器或对抗训练。

3.5.1.2 稳定性

有监督训练的一个优点是非常稳定。当我们加入更复杂的物理模型或研究更复杂的 NN 架构时，情况也不会变得更好。

因此，在开始进行简单的过拟合测试时，请再次确保您能看到训练损失呈指数下降。这是一个很好的设置，可以找出作为最核心超参数的学习率的上限和合理范围。以后你可能还需要降低学习率，但至少应该能大致估算出 $η$ 的合适值。

3.5.1.3 了解你的数据

所有数据驱动型方法都遵循 "垃圾进垃圾出 "原则。因此，了解你所处理的数据非常重要。虽然没有放之四海而皆准的最佳方法，但我们强烈建议对数据集进行广泛的统计跟踪。一个好的起点是每个数量的平均值、标准偏差、最小值和最大值。如果其中某些值不正常，则表明数据集中存在不良样本。

这些值也可以很容易地通过直方图进行可视化，以追踪不需要的异常值。少量的异常值很容易使数据集出现偏差。

最后，检查不同数量之间的关系通常是个好主意，这样可以获得数据集所包含内容的一些直觉。下图给出了这一步骤的示例。

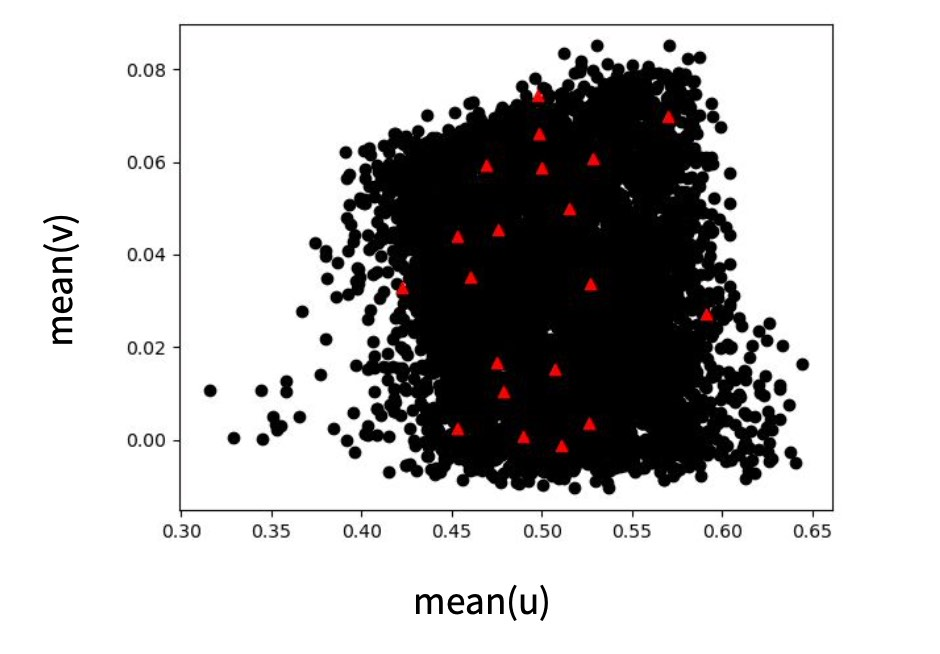
3.5.1.4 魔力在哪里?

在讨论 DL 方法时，尤其是在使用相对简单的训练方法时，你经常会听到这样的评论："这不就是对数据进行插值吗？"

嗯，是的！这正是NN应该做的。从某种程度上说，没有其他事情可做。这就是所有 DL 方法的目的。它们为我们提供训练时所看到的数据的平滑表示。即使我们以后在训练时使用了花哨的物理模型，NN 也只是调整它们的权重来代表它们接收到的信号，并将其再现出来。

由于炒作和大量成功案例，不熟悉 DL 的人往往会产生这样的印象：DL 就像人类的大脑一样工作，能够从数据集中提取基本和一般原理（"上帝的信息" 有人说过吗？）目前的技术水平并非如此。尽管如此，它仍是我们用来逼近复杂非线性函数的最强大工具。它是一个伟大的工具，但重要的是要记住，一旦我们正确设置了训练，我们从中得到的只是 NN 所训练的函数的近似值--不涉及任何魔法。

这意味着，你不应该指望网络能在它从未见过的数据上工作。从某种程度上说，神经网络之所以如此出色，正是因为它们能够准确地适应训练时接收到的信号，但与其他学习到的表征相比，神经网络实际上并不擅长外推。因此，我们不能指望神经网络能神奇地处理新的输入。相反，我们需要确保能够正确塑造输入空间，例如，通过归一化和关注不变量。

举个更具体的例子：如果您总是在 $[0 \dots 1]$ 的范围内训练您的网络输入，那么就不要指望它能在 $[27 \dots 39]$ 的输入下工作。在某些情况下，可以通过减去平均值来对输入和输出进行归一化，并通过标准偏差或合适的量化值进行归一化（确保这不会破坏数据中的重要相关性）。

经验法则：确保在实际训练 NN 时，输入尽可能与推理时要使用的输入相似。

这一点在接下来的章节中必须牢记：例如，如果我们希望 NN 与特定的模拟环境结合使用，那么在训练过程中就必须实际加入模拟器。否则，网络可能会专门处理预先计算的数据，而这些数据与将 NN 与求解器结合时产生的数据不同，即会出现_分布偏移_。

3.1.5.5 网格和栅格

前面的翼型示例使用了带有标准卷积的笛卡尔网格。就性能和稳定性而言，这些通常是最划算的。尽管如此，这里的整个讨论当然也适用于其他类型的卷积，例如，与图卷积结合的不太规则的网格，或具有连续卷积的基于粒子的数据（参见[非结构化网格和无网格方法](http://physicsbaseddeeplearning.org/others lagrangian.html)）。当切换到这些方法时，你通常会看到学习性能降低，以换取采样灵活性的提高。最后，关于全连接层或一般的MLP：我们建议尽可能避免这些。对于任何结构化数据，如空间函数或一般的字段数据，卷积是优选的，并且不太可能过拟合。例如，你会注意到细胞神经网络通常不需要丢弃，因为它们通过构建很好地正则化了。对于MLP，您通常需要相当多的方法来避免过拟合。

3.5.2 监督训练简述

总之，监督训练具有以下特点。

✅ 优点：

训练速度非常快。
稳定简单。
是一个很好的起点。

❌ 缺点：需要大量数据。

性能、准确性和泛化能力不够优秀。
与外部“进程”（如嵌入到求解器中）的交互困难。

接下来的章节将解释如何缓解监督训练的这些缺点。首先，我们将通过软约束将模型方程引入图像中，然后我们将重新审视将数值模拟和学习方法结合起来所面临的挑战。