25.1 概述
我们正在考虑与笔记本《监督型机翼》中相同的设置:研究翼型周围的湍流气流,希望了解在不同雷诺数和攻角下的平均运动和压力分布。在早期的笔记本中,我们通过完全绕过任何物理求解器,而是训练一个神经网络来学习感兴趣的量来解决这个问题。现在,我们想将这种方法扩展到前一节中的变分贝叶斯神经网络(BNNs)。与传统网络不同,传统网络为每个权重值学习一个单点估计值,而BNNs的目标是学习每个权重参数上的分布(例如,具有均值和方差的高斯分布)。在前向传递过程中,网络中的每个参数都从相应的近似后验分布中抽样。从这个意义上讲,网络参数本身是随机变量,每次前向传递都是随机的,因为对于给定的输入,预测结果会在每次前向传递中变化。这可以用来评估网络的“不确定性”:如果预测结果变化很大,我们认为网络对其输出结果不确定。
[在colab中运行] ( https://colab.research.google.com/github/tum-pbs/pbdl-book/blob/main/bayesian-code.ipynb )
25.1.1 读取数据
与之前的笔记本一样,我们将跳过数据生成过程。这个示例改编自Deep-Flow-Prediction代码库,您可以查看详细信息。在这里,我们将简单地下载一小部分使用OpenFOAM中的Spalart-Almaras RANS模拟生成的训练数据。
import numpy as np
import os.path, random
# get training data: as in the previous supervised example, either download or use gdrive
dir = "./"
if True:
if not os.path.isfile('data-airfoils.npz'):
import requests
print("Downloading training data (300MB), this can take a few minutes the first time...")
with open("data-airfoils.npz", 'wb') as datafile:
resp = requests.get('https://dataserv.ub.tum.de/s/m1615239/download?path=%2F&files=dfp-data-400.npz', verify=False)
datafile.write(resp.content)
else: # cf supervised airfoil code:
from google.colab import drive
drive.mount('/content/gdrive')
dir = "./gdrive/My Drive/"
npfile=np.load(dir+'data-airfoils.npz')
print("Loaded data, {} training, {} validation samples".format(len(npfile["inputs"]),len(npfile["vinputs"])))
print("Size of the inputs array: "+format(npfile["inputs"].shape))
# reshape to channels_last for convencience
X_train = np.moveaxis(npfile["inputs"],1,-1)
y_train = np.moveaxis(npfile["targets"],1,-1)
X_val = np.moveaxis(npfile["vinputs"],1,-1)
y_val = np.moveaxis(npfile["vtargets"],1,-1)
Downloading training data (300MB), this can take a few minutes the first time...
Loaded data, 320 training, 80 validation samples
Size of the inputs array: (320, 3, 128, 128)
25.1.2 查看数据
现在我们有一些训练数据。我们可以使用在原始笔记本中所用的代码来查看它。
import pylab
from matplotlib import cm
# helper to show three target channels: normalized, with colormap, side by side
def showSbs(a1,a2, bottom="NN Output", top="Reference", title=None):
c=[]
for i in range(3):
b = np.flipud( np.concatenate((a2[...,i],a1[...,i]),axis=1).transpose())
min, mean, max = np.min(b), np.mean(b), np.max(b);
b -= min; b /= (max-min)
c.append(b)
fig, axes = pylab.subplots(1, 1, figsize=(16, 5))
axes.set_xticks([]); axes.set_yticks([]);
im = axes.imshow(np.concatenate(c,axis=1), origin='upper', cmap='magma')
pylab.colorbar(im); pylab.xlabel('p, ux, uy'); pylab.ylabel('%s %s'%(bottom,top))
if title is not None: pylab.title(title)
NUM=40
print("\nHere are all 3 inputs are shown at the top (mask,in x, in y) \nSide by side with the 3 output channels (p,vx,vy) at the bottom:")
showSbs( X_train[NUM],y_train[NUM], bottom="Target Output", top="Inputs", title="Training data sample")
Here are all 3 inputs are shown at the top (mask,in x, in y)
Side by side with the 3 output channels (p,vx,vy) at the bottom:

不出所料, 数据看起来仍然相同。有关详细信息, 请查看{doc} supervised-airfoils 中的描述。
25.1.3 神经网络定义
现在让我们来看看如何实现BNNs(贝叶斯神经网络)。与PyTorch不同,我们将使用TensorFlow,特别是TensorFlow Probability扩展,它具有易于实现的概率层。与另一个笔记本类似,我们使用一个由具有跳跃连接的卷积块组成的U-Net结构。目前,我们只想将解码器设置为贝叶斯部分,也就是U-Net的第二部分。为此,我们将利用TensorFlow的flipout层(特别是卷积实现)。
在前向传播中,这些层会自动从当前后验分布中进行采样,并将先验与后验之间的KL散度存储在_model.losses_中。如果希望使用非正态分布以外的其他先验和近似后验分布,可以指定所需的散度度量(通常是KL散度)并进行修改。除此之外,flipout层可以像顺序结构中的常规层一样使用。下面的代码实现了U-Net的单个卷积块:
import tensorflow as tf
import tensorflow_probability.python.distributions as tfd
from tensorflow.keras import Sequential
from tensorflow.keras.initializers import RandomNormal
from tensorflow.keras.layers import Input, Conv2D, Conv2DTranspose,UpSampling2D, BatchNormalization, ReLU, LeakyReLU, SpatialDropout2D, MaxPooling2D
from tensorflow_probability.python.layers import Convolution2DFlipout
from tensorflow.keras.models import Model
def tfBlockUnet(filters=3, transposed=False, kernel_size=4, bn=True, relu=True, pad="same", dropout=0., flipout=False,
kdf=None, name=''):
block = Sequential(name=name)
if relu:
block.add(ReLU())
else:
block.add(LeakyReLU(0.2))
if not transposed:
block.add(Conv2D(filters=filters, kernel_size=kernel_size, padding=pad,
kernel_initializer=RandomNormal(0.0, 0.02), activation=None,strides=(2,2)))
else:
block.add(UpSampling2D(interpolation = 'bilinear'))
if flipout:
block.add(Convolution2DFlipout(filters=filters, kernel_size=(kernel_size-1), strides=(1, 1), padding=pad,
data_format="channels_last", kernel_divergence_fn=kdf,
activation=None))
else:
block.add(Conv2D(filters=filters, kernel_size=(kernel_size-1), padding=pad,
kernel_initializer=RandomNormal(0.0, 0.02), strides=(1,1), activation=None))
block.add(SpatialDropout2D(rate=dropout))
if bn:
block.add(BatchNormalization(axis=-1, epsilon=1e-05,momentum=0.9))
return block
接下来,我们使用这些模块定义完整的网络结构,其结构与之前的笔记本几乎完全相同。我们手动定义了名为kdf的核散度函数,并用一个名为kl_scaling的因子对其进行了缩放。这样做有两个原因:
首先,如果我们要使用正确的损失(如在{doc}bayesian-intro中介绍的),我们应该每个周期只应用一次KL散度。由于我们将使用基于批次的训练,因此需要将KL散度按批次数量进行缩放,以便在每次参数更新中,只有kdf / num_batches被添加到损失中。在一个周期内,会执行num_batches次参数更新,并使用“完整的”KL散度。这个批次缩放值通过在稍后实例化Bayes_DfpNet 神经网络时,通过kl_scaling传递给网络初始化。
其次,通过调整损失函数中的KL散度部分的比例,我们可以调整网络中允许的随机性程度:如果完全忽略KL散度,我们将只是最小化常规损失(例如MSE或MAE),就像在传统神经网络中一样。如果我们忽略负对数似然,我们将优化网络,以便从先验分布中获得随机抽样。通过对KL散度的缩放进行平衡,可以调整这些极端情况,但实践中很困难。
def Bayes_DfpNet(input_shape=(128,128,3),expo=5,dropout=0.,flipout=False,kl_scaling=10000):
channels = int(2 ** expo + 0.5)
kdf = (lambda q, p, _: tfd.kl_divergence(q, p) / tf.cast(kl_scaling, dtype=tf.float32))
layer1=Sequential(name='layer1')
layer1.add(Conv2D(filters=channels,kernel_size=4,strides=(2,2),padding='same',activation=None,data_format='channels_last'))
layer2=tfBlockUnet(filters=channels*2,transposed=False,bn=True, relu=False,dropout=dropout,name='layer2')
layer3=tfBlockUnet(filters=channels*2,transposed=False,bn=True, relu=False,dropout=dropout,name='layer3')
layer4=tfBlockUnet(filters=channels*4,transposed=False,bn=True, relu=False,dropout=dropout,name='layer4')
layer5=tfBlockUnet(filters=channels*8,transposed=False,bn=True, relu=False,dropout=dropout,name='layer5')
layer6=tfBlockUnet(filters=channels*8,transposed=False,bn=True, relu=False,dropout=dropout,kernel_size=2,pad='valid',name='layer6')
layer7=tfBlockUnet(filters=channels*8,transposed=False,bn=True, relu=False,dropout=dropout,kernel_size=2,pad='valid',name='layer7')
# note, kernel size is internally reduced by one for the decoder part
dlayer7=tfBlockUnet(filters=channels*8,transposed=True,bn=True, relu=True,dropout=dropout, flipout=flipout,kdf=kdf, kernel_size=2,pad='valid',name='dlayer7')
dlayer6=tfBlockUnet(filters=channels*8,transposed=True,bn=True, relu=True,dropout=dropout, flipout=flipout,kdf=kdf, kernel_size=2,pad='valid',name='dlayer6')
dlayer5=tfBlockUnet(filters=channels*4,transposed=True,bn=True, relu=True,dropout=dropout, flipout=flipout,kdf=kdf,name='dlayer5')
dlayer4=tfBlockUnet(filters=channels*2,transposed=True,bn=True, relu=True,dropout=dropout, flipout=flipout,kdf=kdf,name='dlayer4')
dlayer3=tfBlockUnet(filters=channels*2,transposed=True,bn=True, relu=True,dropout=dropout, flipout=flipout,kdf=kdf,name='dlayer3')
dlayer2=tfBlockUnet(filters=channels ,transposed=True,bn=True, relu=True,dropout=dropout, flipout=flipout,kdf=kdf,name='dlayer2')
dlayer1=Sequential(name='outlayer')
dlayer1.add(ReLU())
dlayer1.add(Conv2DTranspose(3,kernel_size=4,strides=(2,2),padding='same'))
# forward pass
inputs=Input(input_shape)
out1 = layer1(inputs)
out2 = layer2(out1)
out3 = layer3(out2)
out4 = layer4(out3)
out5 = layer5(out4)
out6 = layer6(out5)
out7 = layer7(out6)
# ... bottleneck ...
dout6 = dlayer7(out7)
dout6_out6 = tf.concat([dout6,out6],axis=3)
dout6 = dlayer6(dout6_out6)
dout6_out5 = tf.concat([dout6, out5], axis=3)
dout5 = dlayer5(dout6_out5)
dout5_out4 = tf.concat([dout5, out4], axis=3)
dout4 = dlayer4(dout5_out4)
dout4_out3 = tf.concat([dout4, out3], axis=3)
dout3 = dlayer3(dout4_out3)
dout3_out2 = tf.concat([dout3, out2], axis=3)
dout2 = dlayer2(dout3_out2)
dout2_out1 = tf.concat([dout2, out1], axis=3)
dout1 = dlayer1(dout2_out1)
return Model(inputs=inputs,outputs=dout1)
让我们定义超参数并创建一个 TensorFlow 数据集来组织输入和目标。由于训练集中有 320 个观测值,对于批次大小为 10,我们应该将 KL 散度按比例缩放为 320/10=32,以便每个周期只应用一次完整的 KL 散度。此外,我们还将通过一个名为 KL_PREF=5000 的因子进一步将 KL 散度缩小,该因子在实践中已经被证明效果良好。
此外,我们将定义一个实现学习率衰减的函数。直观地说,这使得优化在后续epoch中更精确(通过更小的步长),同时在前几个epoch中仍然能够快速进展(通过更大的步长)。
import math
import matplotlib.pyplot as plt
BATCH_SIZE=10
LR=0.001
EPOCHS = 120
KL_PREF = 5000
dataset = tf.data.Dataset.from_tensor_slices((X_train, y_train)).shuffle(len(X_train),
seed=46168531, reshuffle_each_iteration=False).batch(BATCH_SIZE, drop_remainder=False)
def compute_lr(i, epochs, minLR, maxLR):
if i < epochs * 0.5:
return maxLR
e = (i / float(epochs) - 0.5) * 2.
# rescale second half to min/max range
fmin = 0.
fmax = 6.
e = fmin + e * (fmax - fmin)
f = math.pow(0.5, e)
return minLR + (maxLR - minLR) * f
我们可以可视化学习率衰减:我们从一个恒定的学习率开始,在 EPOCHS 的一半之后,我们开始指数衰减学习率,直到达到原始学习率的一半。
lrs=[compute_lr(i, EPOCHS, 0.5*LR,LR) for i in range(EPOCHS)]
plt.plot(lrs)
plt.xlabel('Iteration')
plt.ylabel('Learning Rate')
让我们初始化网络。在这里, 我们最终通过 KL_PREF 和批量大小计算 kl_scaling 因子。
from tensorflow.keras.optimizers import RMSprop, Adam
model=Bayes_DfpNet(expo=4,flipout=True,kl_scaling=KL_PREF*len(X_train)/BATCH_SIZE)
optimizer = Adam(learning_rate=LR, beta_1=0.5,beta_2=0.9999)
num_params = np.sum([np.prod(v.get_shape().as_list()) for v in model.trainable_variables])
print('The Bayesian U-Net has {} parameters.'.format(num_params))
一般来说,与其传统对应物相比,翻转层的参数是两倍,因为不仅需要学习高斯后验权重的均值和方差参数,还需要学习单点估计。由于这里我们只对解码器部分使用了翻转层, 生成的模型具有 846787 个参数,而传统 NN 具有 585667 个参数。
25.2 训练
现在我们准备开始训练!请注意,这可能需要一些时间(通常约为4小时),因为与常规层相比,翻转层的训练速度较慢。
from tensorflow.keras.losses import mae
import math
kl_losses=[]
mae_losses=[]
total_losses=[]
mae_losses_vali=[]
for epoch in range(EPOCHS):
# compute learning rate - decay is implemented
currLr = compute_lr(epoch,EPOCHS,0.5*LR,LR)
if currLr < LR:
tf.keras.backend.set_value(optimizer.lr, currLr)
# iterate through training data
kl_sum = 0
mae_sum = 0
total_sum=0
for i, traindata in enumerate(dataset, 0):
# forward pass and loss computation
with tf.GradientTape() as tape:
inputs, targets = traindata
prediction = model(inputs, training=True)
loss_mae = tf.reduce_mean(mae(prediction, targets))
kl=sum(model.losses)
loss_value=kl+tf.cast(loss_mae, dtype='float32')
# backpropagate gradients and update parameters
gradients = tape.gradient(loss_value, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))
# store losses per batch
kl_sum += kl
mae_sum += tf.reduce_mean(loss_mae)
total_sum+=tf.reduce_mean(loss_value)
# store losses per epoch
kl_losses+=[kl_sum/len(dataset)]
mae_losses+=[mae_sum/len(dataset)]
total_losses+=[total_sum/len(dataset)]
# validation
outputs = model.predict(X_val)
mae_losses_vali += [tf.reduce_mean(mae(y_val, outputs))]
if epoch<3 or epoch%20==0:
print('Epoch {}/{}, total loss: {:.3f}, KL loss: {:.3f}, MAE loss: {:.4f}, MAE loss vali: {:.4f}'.format(epoch, EPOCHS, total_losses[-1], kl_losses[-1], mae_losses[-1], mae_losses_vali[-1]))
Epoch 0/120, total loss: 4.265, KL loss: 4.118, MAE loss: 0.1464, MAE loss vali: 0.0872
Epoch 1/120, total loss: 4.159, KL loss: 4.089, MAE loss: 0.0706, MAE loss vali: 0.0691
Epoch 2/120, total loss: 4.115, KL loss: 4.054, MAE loss: 0.0610, MAE loss vali: 0.0589
Epoch 20/120, total loss: 3.344, KL loss: 3.315, MAE loss: 0.0291, MAE loss vali: 0.0271
Epoch 40/120, total loss: 2.495, KL loss: 2.471, MAE loss: 0.0245, MAE loss vali: 0.0242
Epoch 60/120, total loss: 1.712, KL loss: 1.689, MAE loss: 0.0228, MAE loss vali: 0.0208
Epoch 80/120, total loss: 1.190, KL loss: 1.169, MAE loss: 0.0212, MAE loss vali: 0.0200
Epoch 100/120, total loss: 0.869, KL loss: 0.848, MAE loss: 0.0208, MAE loss vali: 0.0203
BNN已经训练完毕!让我们来看一下损失。由于损失由两个独立的部分组成,监控这两个部分(MAE和KL)是很有帮助的。
fig,axs=plt.subplots(ncols=3,nrows=1,figsize=(20,4))
axs[0].plot(kl_losses,color='red')
axs[0].set_title('KL Loss (Train)')
axs[1].plot(mae_losses,color='blue',label='train')
axs[1].plot(mae_losses_vali,color='green',label='val')
axs[1].set_title('MAE Loss'); axs[1].legend()
axs[2].plot(total_losses,label='Total',color='black')
axs[2].plot(kl_losses,label='KL',color='red')
axs[2].plot(mae_losses,label='MAE',color='blue')
axs[2].set_title('Total Train Loss'); axs[2].legend()
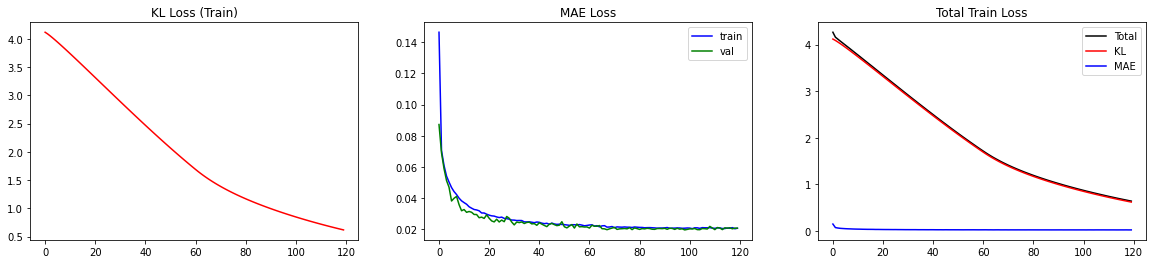
这样,我们可以进行双重检查,以确定减小损失的一个部分是否以增加另一个部分为代价。对于我们的情况,我们观察到两个部分都在平稳下降。特别是,MAE损失对于验证集而言并没有增加,这表明我们没有过拟合。
双重检查添加了多少层KL损失是一个好的实践。我们可以检查_model.losses来了解。由于解码器由6个连续块和flipout层组成,我们预计_model.losses中会有6个条目。
# there should be 6 entries in model.losses since we have 6 blocks with flipout layers in our model
print('There are {} entries in model.losses'.format(len(model.losses)))
print(model.losses)
There are 6 entries in model.losses
[<tf.Tensor: shape=(), dtype=float32, numpy=0.03536303>, <tf.Tensor: shape=(), dtype=float32, numpy=0.06506929>, <tf.Tensor: shape=(), dtype=float32, numpy=0.2647468>, <tf.Tensor: shape=(), dtype=float32, numpy=0.09337218>, <tf.Tensor: shape=(), dtype=float32, numpy=0.0795429>, <tf.Tensor: shape=(), dtype=float32, numpy=0.075103864>]
现在让我们来可视化一下BNN在验证集中的未知数据上的性能。理想情况下,我们希望将参数积分掉,即进行边缘化以获得预测结果。由于这在分析上很难实现,通常会通过从后验中进行采样来近似积分:
在实践中,这意味着对于每个输入,执行次前向传递,并计算平均值,其中每个是从中抽取的。以同样的精神,可以通过标准差来衡量不确定性:
请注意,和仍然具有形状,即均值和方差计算是按像素进行的(但可能在之后聚合为全局度量)。
REPS=20
preds=np.zeros(shape=(REPS,)+X_val.shape)
for rep in range(REPS):
preds[rep,:,:,:,:]=model.predict(X_val)
preds_mean=np.mean(preds,axis=0)
preds_std=np.std(preds,axis=0)
在检查前一个单元格中计算出的平均值和标准偏差之前,让我们可视化BNN的一个输出。在下面的图中,第一行显示输入,而第二行说明单次前向传递的结果。
NUM=16
# show a single prediction
showSbs(y_val[NUM],preds[0][NUM], top="Inputs", bottom="Single forward pass")
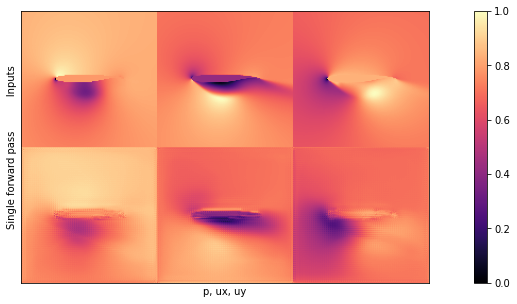
如果你将这个图像与{doc}supervised-airfoils中的输出进行比较,你会发现乍一看它们并没有太大的区别。这是一个好兆头,似乎网络已经学会了生成压力和速度场的内容。
然而,更重要的是,我们现在可以通过检查后验分布中的几个样本以及给定输入的标准差,更清楚地可视化预测的不确定性。下面是一个用于准确可视化的函数代码(为了突出与之前的非贝叶斯笔记本的差异,不确定性使用了不同的颜色映射)。
# plot repeated samples from posterior for some observations
def plot_BNN_predictions(target, preds, pred_mean, pred_std, num_preds=5,channel=0):
if num_preds>len(preds):
print('num_preds was set to {}, but has to be smaller than the length of preds. Setting it to {}'.format(num_preds,len(preds)))
num_preds = len(preds)
# transpose and concatenate the frames that are to plot
to_plot=np.concatenate((target[:,:,channel].transpose().reshape(128,128,1),preds[0:num_preds,:,:,channel].transpose(),
pred_mean[:,:,channel].transpose().reshape(128,128,1),pred_std[:,:,channel].transpose().reshape(128,128,1)),axis=-1)
fig, axs = plt.subplots(nrows=1,ncols=to_plot.shape[-1],figsize=(20,4))
for i in range(to_plot.shape[-1]):
label='Target' if i==0 else ('Avg Pred' if i == (num_preds+1) else ('Std Dev (normalized)' if i == (num_preds+2) else 'Pred {}'.format(i)))
colmap = cm.viridis if i==to_plot.shape[-1]-1 else cm.magma
frame = np.flipud(to_plot[:,:,i])
min=np.min(frame); max = np.max(frame)
frame -= min; frame /=(max-min)
axs[i].imshow(frame,cmap=colmap)
axs[i].axis('off')
axs[i].set_title(label)
OBS_IDX=5
plot_BNN_predictions(y_val[OBS_IDX,...],preds[:,OBS_IDX,:,:,:],preds_mean[OBS_IDX,...],preds_std[OBS_IDX,...])

我们正在查看通道0,也就是压力。可以观察到在不同的预测中,暗区和亮区变化相当大。令人欣慰的是,至少从视觉检查来看,平均(边缘)预测比大多数单次正向传递更接近目标。
还需要注意的是,每个帧都经过了归一化处理以进行可视化。因此,当观察不确定性帧时,我们可以推断出网络在哪些地方不确定,但不能确定其绝对值的不确定程度。为了评估不确定性的全局度量,我们可以计算验证集中所有样本的平均标准差。
# Average Prediction with total uncertainty
uncertainty_total = np.mean(np.abs(preds_std),axis=(0,1,2))
preds_mean_global = np.mean(np.abs(preds),axis=(0,1,2,3))
print("\nAverage pixel prediction on validation set: \n pressure: {} +- {}, \n ux: {} +- {},\n uy: {} +- {}".format(np.round(preds_mean_global[0],3),np.round(uncertainty_total[0],3),np.round(preds_mean_global[1],3),np.round(uncertainty_total[1],3),np.round(preds_mean_global[2],3),np.round(uncertainty_total[2],3)))
Average pixel prediction on validation set:
pressure: 0.025 +- 0.009,
ux: 0.471 +- 0.019,
uy: 0.081 +- 0.016
对于使用标准设置的运行,三个场的不确定性大约在0.01的数量级上。由于压力场的均值较小,相对而言其不确定性更大。这是有道理的,因为众所周知,压力场比两个速度分量更难预测。
25.3 测试评估
就像对于传统神经网络一样,现在让我们来看一下合适的测试样本,也就是OOD样本,对于这些样本,我们将使用新的翼型。这些翼型是网络在任何训练样本中都没有见过的,因此它可以告诉我们网络对新形状的泛化能力如何。
由于这些样本至少在某种程度上属于OOD,我们可以得出关于网络泛化能力的结论,而这是验证数据无法告诉我们的。特别是,我们想要调查神经网络在处理OOD数据时是否更加不确定。与之前一样,我们首先下载测试样本...
if not os.path.isfile('data-airfoils-test.npz'):
import urllib.request
url="https://physicsbaseddeeplearning.org/data/data_test.npz"
print("Downloading test data, this should be fast...")
urllib.request.urlretrieve(url, 'data-airfoils-test.npz')
nptfile=np.load('data-airfoils-test.npz')
print("Loaded {}/{} test samples".format(len(nptfile["test_inputs"]),len(nptfile["test_targets"])))
Downloading test data, this should be fast...
Loaded 10/10 test samples
...然后重复上述步骤,对测试样本进行BNN评估,并计算边缘化的预测和不确定性。
X_test = np.moveaxis(nptfile["test_inputs"],1,-1)
y_test = np.moveaxis(nptfile["test_targets"],1,-1)
REPS=10
preds_test=np.zeros(shape=(REPS,)+X_test.shape)
for rep in range(REPS):
preds_test[rep,:,:,:,:]=model.predict(X_test)
preds_test_mean=np.mean(preds_test,axis=0)
preds_test_std=np.std(preds_test,axis=0)
test_loss = tf.reduce_mean(mae(preds_test_mean, y_test))
print("\nAverage test error: {}".format(test_loss))
Average test error: 0.023046530292471824
# Average Prediction with total uncertainty
uncertainty_test_total = np.mean(np.abs(preds_test_std),axis=(0,1,2))
preds_test_mean_global = np.mean(np.abs(preds_test),axis=(0,1,2,3))
print("\nAverage pixel prediction on test set: \n pressure: {} +- {}, \n ux: {} +- {},\n uy: {} +- {}".format(np.round(preds_test_mean_global[0],3),np.round(uncertainty_test_total[0],3),np.round(preds_test_mean_global[1],3),np.round(uncertainty_test_total[1],3),np.round(preds_test_mean_global[2],3),np.round(uncertainty_test_total[2],3)))
Average pixel prediction on test set:
pressure: 0.03 +- 0.012,
ux: 0.466 +- 0.024,
uy: 0.091 +- 0.02
这是令人欣慰的:在具有新形状的OOD测试集上,不确定性至少略高于验证集。
25.3.1 可视化
下面的图表可视化了这些度量结果:它将验证集和测试集的平均绝对误差并排显示,同时使用误差线表示预测的不确定性:
# plot per channel MAE with uncertainty
val_loss_c, test_loss_c = [], []
for channel in range(3):
val_loss_c.append( tf.reduce_mean(mae(preds_mean[...,channel], y_val[...,channel])) )
test_loss_c.append( tf.reduce_mean(mae(preds_test_mean[...,channel], y_test[...,channel])) )
fig, ax = plt.subplots()
ind = np.arange(len(val_loss_c)); width=0.3
bars1 = ax.bar(ind - width/2, val_loss_c, width, yerr=uncertainty_total, capsize=4, label="validation")
bars2 = ax.bar(ind + width/2, test_loss_c, width, yerr=uncertainty_test_total, capsize=4, label="test")
ax.set_ylabel("MAE & Uncertainty")
ax.set_xticks(ind); ax.set_xticklabels(('P', 'u_x', 'u_y'))
ax.legend(); plt.tight_layout()
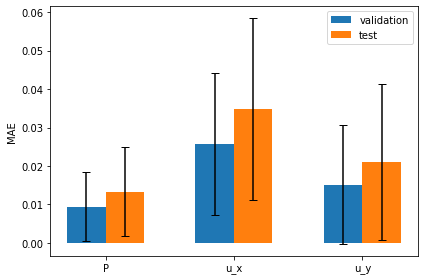
平均误差显然更大,而预测的稍大不确定性也通过误差线呈现出来。
一般来说,获得校准的不确定性估计是困难的,但由于我们处理的是一个相当简单的问题,BNN能够相当好地估计不确定性。
下一个图表展示了测试集中单个案例的BNN预测差异(使用与上述验证样本相同的样式):
OBS_IDX=5
plot_BNN_predictions(y_test[OBS_IDX,...],preds_test[:,OBS_IDX,:,:,:],preds_test_mean[OBS_IDX,...],preds_test_std[OBS_IDX,...])
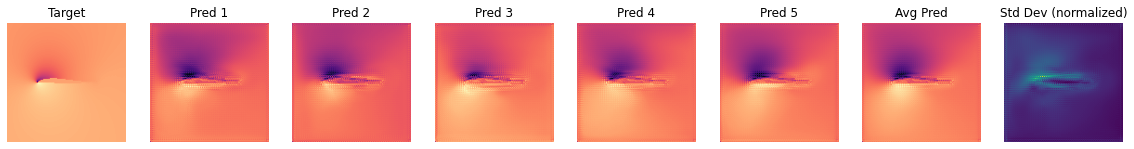
我们还可以将测试集中的几个形状与相应的边缘化预测和不确定性一起进行可视化。
IDXS = [1,3,8]
CHANNEL = 0
fig, axs = plt.subplots(nrows=len(IDXS),ncols=3,sharex=True, sharey = True, figsize = (9,len(IDXS)*3))
for i, idx in enumerate(IDXS):
axs[i][0].imshow(np.flipud(X_test[idx,:,:,CHANNEL].transpose()), cmap=cm.magma)
axs[i][1].imshow(np.flipud(preds_test_mean[idx,:,:,CHANNEL].transpose()), cmap=cm.magma)
axs[i][2].imshow(np.flipud(preds_test_std[idx,:,:,CHANNEL].transpose()), cmap=cm.viridis)
axs[0][0].set_title('Shape')
axs[0][1].set_title('Avg Pred')
axs[0][2].set_title('Std. Dev')
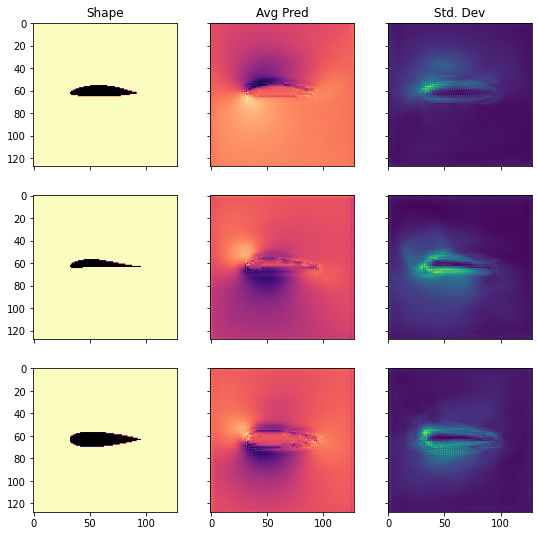
正如我们所看到的,测试集中的形状彼此之间有很大的差异。然而,不确定性估计相对合理地分布。它在翼型周围的边界层和低压区域尤为明显。
25.3.2 讨论
尽管这些结果令人鼓舞,贝叶斯神经网络仍存在一些问题,限制了它们在许多实际应用中的使用。其中一个严重的缺点是需要对KL损失进行额外的缩放,而且目前还没有令人信服的理由说明为什么这是必要的(详见这里 或 这里)。
此外,一些人认为将独立正态分布作为后验的变分近似是一种过度简化,因为在实践中,权重实际上是高度相关的(参考论文)。而其他一些人则认为,只要使用的网络足够深,这可能并不是一个问题(参考论文)。此外,还有关于BNN的许多其他方面的研究,例如使用不同的先验(如重尾分布)等。
25.4 下一步
现在是时候自己进行贝叶斯神经网络的实验了。
-
一个有趣的方面是观察我们的贝叶斯神经网络在调整KL预乘因子后的行为变化。在上面的训练循环中,我们将其设置为5000,但没有进一步的理由解释。你可以尝试使用理论建议的值1来替代5000,看看会发生什么变化。根据我们的实现,这样做应该使网络更具"贝叶斯"特性,因为我们赋予KL散度更大的重要性。
-
到目前为止,我们只使用了通过TensorFlow概率层来实现的变分贝叶斯神经网络。回想一下,还有一种更简单的方法来获得不确定性估计:不仅在训练时使用dropout,而且在推断时也使用dropout。你可以观察一下在这种情况下输出的变化。为了实现这个,你可以在网络规范中设置一个非零的dropout率,并将上面的预测阶段从_model.predict(...)更改为_model(..., training=True)。设置_training=True标志将告诉TensorFlow将输入视为训练数据,因此会应用dropout。请注意,training=True标志也会影响网络的其他特性。例如,批归一化在训练和预测模式下的工作方式是不同的。只要我们处理的数据差异不大,并且使用足够大的批量大小,这不会引入较大的误差。开始尝试的合理dropout率可能在0.1左右。