在这个例子中，我们将针对在连续偏微分方程${\mathcal{P}}^{\ast }$ 离散化时出现的数值误差进行处理，即当我们构建$\mathcal{P}$ 时。这种方法将证明，尽管缺乏封闭形式的描述，离散化误差通常是具有规则和重复结构的函数，因此可以通过神经网络进行学习。一旦网络训练完成，它可以在本地进行评估，以改善PDE求解器的解，即减少其数值误差。由此产生的方法是一种混合方法：它将始终运行（粗略的）PDE求解器，然后在运行时通过NN推断的修正来改进它。

几乎所有数值方法都包含某种形式的迭代过程：对于显式求解器，需要在时间上重复更新；对于隐式求解器，需要在单个更新步内进行迭代。第二种情况的示例可以在此处找到，但下面我们将针对第一种情况，即时间上的迭代。

run in colab

12.1 问题表述

在减少误差的背景下，拥有一个可微分的物理求解器非常重要，这样学习过程才能考虑到求解器的反应。这种交互在监督学习或PINN训练中是不可能的。即使是监督型神经网络的小推理误差也会随着时间的推移而累积，并导致数据分布与预计算数据的分布不同。这种分布偏移会导致次优结果，甚至会导致求解器崩溃。

为了学习误差函数，我们将考虑同一偏微分方程${\mathcal{P}}^{\ast }$的两种不同离散方式：一个我们认为准确的参考版本，具有离散化版本${\mathcal{P}}_r$和解$\mathbf{r}\in \mathcal{R}$，其中$\mathcal{R}$表示${\mathcal{P}}_r$的解流形。与此同时，我们有同一PDE的不太准确的近似，我们将其称为“源”版本，因为这将是我们的NN后来要与之交互的求解器。类似地，我们有${\mathcal{P}}_s$和解$\mathbf{s}\in \mathcal{S}$。在训练后，我们将获得一个“混合”求解器，它使用${\mathcal{P}}_s$与训练好的网络结合使用，以获得改进的解，即更接近${\mathcal{P}}_r$产生的解。

假设$\mathcal{P}$通过时间步长$\Delta t$推进了一个解，这里将$n$个连续步骤表示为上标：${\mathcal{P}}_s^n(\mathcal{T}{\mathbf{r}}_t)={\mathcal{P}}_s({\mathcal{P}}_s(\cdots {\mathcal{P}}_s(\mathcal{T}{\mathbf{r}}_t)\cdots )).$ 对应的模拟状态为${\mathbf{s}}_{t+n}={\mathcal{P}}^n(\mathcal{T}{\mathbf{r}}_t).$ 在这里，我们假设存在一个映射算子$\mathcal{T}$，其可以将参考解转移到源流形上。例如，这可以是一个简单的下采样操作。特别是对于较长的序列，即较大的$n$，源状态${\mathbf{s}}_{t+n}$将偏离相应的参考状态${\mathbf{r}}_{t+n}$。这就是我们接下来将用NN解决的问题。

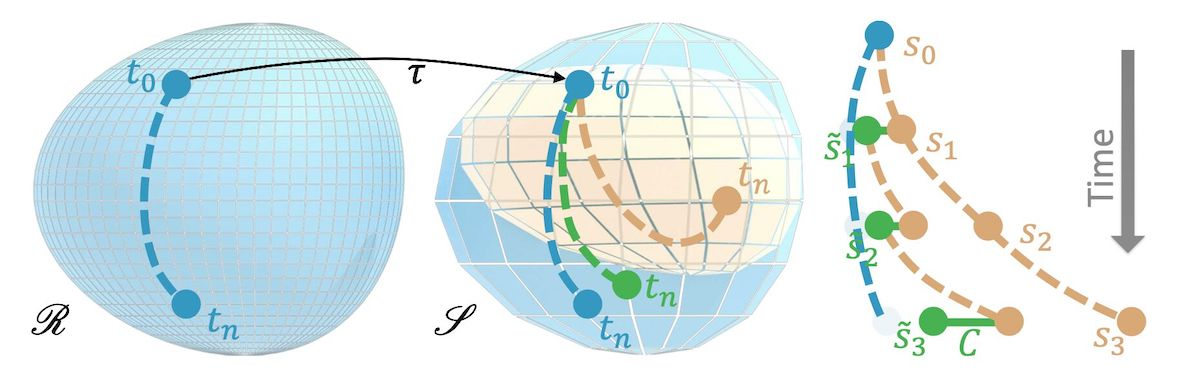
像以前一样, 我们将使用 $L^2$ 范数来量化偏差, 即误差函数 $e\left({\mathbf{s}}_t,\mathcal{T}{\mathbf{r}}_t\right)={\Vert {\mathbf{s}}_t-\mathcal{T}{\mathbf{r}}_t\Vert }_2$。

我们的学习目标是训练一个校正算子 $\mathcal{C}(\mathbf{s})$，应用校正后的解比原始未经修改的 (源)解具有更低的误差: $e\left({\mathcal{P}}_s\left(\mathcal{C}\left(\mathcal{T}{\mathbf{r}}_t\right)\right),\mathcal{T}{\mathbf{r}}_{t+1}\right)<e\left({\mathcal{P}}_s\left(\mathcal{T}{\mathbf{r}}_t\right),\mathcal{T}{\mathbf{r}}_{t+1}\right)$。

修正函数 $\mathcal{C}(\mathbf{s}|\theta )$ 表示为具有权重 $\theta$ 的深度神经网络，接收状态 $\mathbf{s}$ 并推断出具有相同维度的加性修正场。

为了区分原始状态 $\mathbf{s}$ 和修正后的状态，我们将后者用加了波浪线的符号 $\mathbf{s}$ 表示。现在，总体学习目标变为 $${\text{arg min}}_{\theta }(({\mathcal{P}}_s\mathcal{C}{)}^n(\mathcal{T}{\mathbf{r}}_t)-\mathcal{T}{\mathbf{r}}_{t+n}{)}^2$$ 为了简化符号，我们在此省略了对不同样本的求和（即以前版本中的 $i$）。在上述方程中容易被忽视的关键部分是，修正取决于修改后的状态，即它是 $\mathbf{s}$ 的函数，因此我们有 $\mathcal{C}(\tilde{\mathbf{s}}|\theta )$。

这些状态在训练过程中实际上会随时间演化，它们事先并不存在。

我们将训练一个网络 $\mathcal{C}$来降低模拟器的数值误差，并使用更准确的参考进行训练。关键是将源求解器实现为微分物理运算符，以便为改进 $\mathcal{C}$ 的训练提供梯度。

12.2 开始实现

以下是从Solver-in-the-loop：从可微分物理学习与迭代PDE求解器交互 {cite}holl2019pdecontrol中复制的实验，更多细节可以在论文的附录B.1中找到（https://arxiv.org/pdf/2007.00016.pdf）。

首先，让我们下载准备好的数据集（有关生成和加载的详细信息，请参见https://github.com/tum-pbs/Solver-in-the-Loop），然后让我们解决数据处理问题，以便我们可以专注于“有趣”的部分...

import os, sys, logging, argparse, pickle, glob, random, distutils.dir_util, urllib.request

fname_train = 'sol-karman-2d-train.pickle'
if not os.path.isfile(fname_train):
  print("Downloading training data (73MB), this can take a moment the first time...")
  urllib.request.urlretrieve("https://physicsbaseddeeplearning.org/data/"+fname_train, fname_train)

with open(fname_train, 'rb') as f: data_preloaded = pickle.load(f)
print("Loaded data, {} training sims".format(len(data_preloaded)) )

执行结果：

Downloading training data (73MB), this can take a moment the first time...
Loaded data, 6 training sims

同时让我们安装/导入所有必要的库。我们设置随机种子，这里设置的是42。

!pip install --upgrade --quiet phiflow==2.2
from phi.tf.flow import *
import tensorflow as tf
from tensorflow import keras

random.seed(42) 
np.random.seed(42)
tf.random.set_seed(42)

12.3 模拟设置

现在我们设置源模拟${\mathcal{P}}_s$。请注意，我们不会在下面处理${\mathcal{P}}_r$：下采样的参考数据包含在训练数据集中。它是用四倍的离散化生成的。下面，我们将重点关注源求解器和NN的交互。这个代码块和下一个代码块将定义许多函数，稍后将用于训练。

下面的KarmanFlow求解器模拟了一个相对标准的尾流情况，其中一个球形障碍物位于矩形域内，并使用显式粘度求解来获得不同的雷诺数。这是设置的几何形状：

求解器使用预乘掩码(vel_BcMask)为y-速度应用入流边界条件，以在模拟步骤期间设置域底部的y分量。该掩码是使用phiflow中的HardGeometryMask创建的，该掩码正确初始化了交错网格的分量的空间偏移条目。模拟步骤非常直接：它计算粘度、入流、对流的贡献，最后通过隐式压力求解使得结果运动无散。

class KarmanFlow():
    def __init__(self, domain):
        self.domain = domain

        self.vel_BcMask = self.domain.staggered_grid(HardGeometryMask( Box(y=(None, 5), x=None) ) )
    
        self.inflow = self.domain.scalar_grid(Box(y=(25,75), x=(5,10)) ) # scale with domain if necessary!
        self.obstacles = [Obstacle(Sphere(center=tensor([50, 50], channel(vector="y,x")), radius=10))] 
        #

    def step(self, density_in, velocity_in, re, res, buoyancy_factor=0, dt=1.0):
        velocity = velocity_in
        density = density_in

        # viscosity
        velocity = phi.flow.diffuse.explicit(field=velocity, diffusivity=1.0/re*dt*res*res, dt=dt)
        
        # inflow boundary conditions
        velocity = velocity*(1.0 - self.vel_BcMask) + self.vel_BcMask * (1,0)

        # advection 
        density = advect.semi_lagrangian(density+self.inflow, velocity, dt=dt)
        velocity = advected_velocity = advect.semi_lagrangian(velocity, velocity, dt=dt)

        # mass conservation (pressure solve)
        pressure = None
        velocity, pressure = fluid.make_incompressible(velocity, self.obstacles)
        self.solve_info = { 'pressure': pressure, 'advected_velocity': advected_velocity }
        
        return [density, velocity]

12.4 网络架构

我们还将定义两个替代版本的神经网络来表示$\mathcal{C}$。在这两种情况下，我们将使用完全卷积网络，即没有任何全连接层的网络。我们将使用TensorFlow中的Keras来定义网络的层（主要通过Conv2D），分别使用ReLU和LeakyReLU函数进行激活。

网络的输入为：

• 带有x、y速度的2个场
• 雷诺数作为常量通道。

输出为：

• 包含x、y速度的2个分量场。

首先，让我们定义一个仅包含四个ReLU激活的卷积层的小型网络（为简单起见，我们也在这里使用Keras）。输入维度由inputs_dict中的输入张量确定（它有三个通道：u、v和Re）。然后，我们通过三个具有32个特征的卷积层处理数据，然后在输出中将通道减少到2个。

def network_small(inputs_dict):
    l_input = keras.layers.Input(**inputs_dict)
    block_0 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_input)
    block_0 = keras.layers.LeakyReLU()(block_0)

    l_conv1 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(block_0)
    l_conv1 = keras.layers.LeakyReLU()(l_conv1)
    l_conv2 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_conv1)
    block_1 = keras.layers.LeakyReLU()(l_conv2)

    l_output = keras.layers.Conv2D(filters=2,  kernel_size=5, padding='same')(block_1) # u, v
    return keras.models.Model(inputs=l_input, outputs=l_output)

为了灵活性（以及稍后进行更大规模的测试），让我们也定义一个更多层的“正式”的ResNet。这个架构是来自原始论文的，将会给出相当不错的性能（上面的network_small将会训练得更快，但是推理时间会给出次优的性能）。

def network_medium(inputs_dict):
    l_input = keras.layers.Input(**inputs_dict)
    block_0 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_input)
    block_0 = keras.layers.LeakyReLU()(block_0)

    l_conv1 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(block_0)
    l_conv1 = keras.layers.LeakyReLU()(l_conv1)
    l_conv2 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_conv1)
    l_skip1 = keras.layers.add([block_0, l_conv2])
    block_1 = keras.layers.LeakyReLU()(l_skip1)

    l_conv3 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(block_1)
    l_conv3 = keras.layers.LeakyReLU()(l_conv3)
    l_conv4 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_conv3)
    l_skip2 = keras.layers.add([block_1, l_conv4])
    block_2 = keras.layers.LeakyReLU()(l_skip2)

    l_conv5 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(block_2)
    l_conv5 = keras.layers.LeakyReLU()(l_conv5)
    l_conv6 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_conv5)
    l_skip3 = keras.layers.add([block_2, l_conv6])
    block_3 = keras.layers.LeakyReLU()(l_skip3)

    l_conv7 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(block_3)
    l_conv7 = keras.layers.LeakyReLU()(l_conv7)
    l_conv8 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_conv7)
    l_skip4 = keras.layers.add([block_3, l_conv8])
    block_4 = keras.layers.LeakyReLU()(l_skip4)

    l_conv9 = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(block_4)
    l_conv9 = keras.layers.LeakyReLU()(l_conv9)
    l_convA = keras.layers.Conv2D(filters=32, kernel_size=5, padding='same')(l_conv9)
    l_skip5 = keras.layers.add([block_4, l_convA])
    block_5 = keras.layers.LeakyReLU()(l_skip5)

    l_output = keras.layers.Conv2D(filters=2,  kernel_size=5, padding='same')(block_5)
    return keras.models.Model(inputs=l_input, outputs=l_output)

接下来，我们要介绍两个非常重要的函数：它们将模拟状态转换为神经网络的输入张量，反之亦然。因此，它们是keras/tensorflow和phiflow之间的接口。

to_keras函数使用vector['x']和vector['y']中的两个向量分量来丢弃速度场网格的最外层层次。这样就得到了两个相等大小的张量，它们被连接在一起。然后，通过math.ones添加一个常量通道，该通道与ext_const_channel中所需的雷诺数相乘。结果的网格堆栈沿着channels维度堆叠，表示为神经网络的输入。

在网络评估之后，我们通过to_phiflow函数将输出张量转换回phiflow网格。它将网络返回的2分量张量转换为phiflow交错网格对象，以使其与流体模拟的速度场兼容。（注意：这是两个不同大小的_centered_网格，因此我们将工作留给domain.staggered_grid函数，该函数还根据域中给定的物理大小和边界条件进行设置）。

def to_keras(dens_vel_grid_array, ext_const_channel):
    # align the sides the staggered velocity grid making its size the same as the centered grid
    return math.stack(
        [
            math.pad( dens_vel_grid_array[1].vector['x'].values, {'x':(0,1)} , math.extrapolation.ZERO),
            dens_vel_grid_array[1].vector['y'].y[:-1].values,         # v
            math.ones(dens_vel_grid_array[0].shape)*ext_const_channel # Re
        ],
        math.channel('channels')
    )

def to_phiflow(tf_tensor, domain):
    return domain.staggered_grid(
        math.stack(
            [
                math.tensor(tf.pad(tf_tensor[..., 1], [(0,0), (0,1), (0,0)]), math.batch('batch'), math.spatial('y, x')), # v
                math.tensor( tf_tensor[...,:-1, 0], math.batch('batch'), math.spatial('y, x')), # u 
            ], math.channel(vector="y,x")
        ) 
    )

12.5 数据处理

到目前为止一切都很好 - 我们还需要处理一些更加繁琐的任务，例如一些数据处理和随机化。下面我们定义一个Dataset类，它存储所有真值参考数据（已经进行了下采样）。实际上，我们有很多数据维度：多个模拟，有许多时间步长，每个时间步长都有不同的物理场。这使得下面的代码有点难以阅读。

numpy数组dataPreloaded的数据格式是['sim_name'，frame，field（dens ＆ vel）]，其中每个场的维度为[batch-size，y-size，x-size，channels]（这是phiflow导出的标准格式）。

class Dataset():
    def __init__(self, data_preloaded, num_frames, num_sims=None, batch_size=1, is_testset=False):
        self.epoch         = None
        self.epochIdx      = 0
        self.batch         = None
        self.batchIdx      = 0
        self.step          = None
        self.stepIdx       = 0

        self.dataPreloaded = data_preloaded
        self.batchSize     = batch_size

        self.numSims       = num_sims
        self.numBatches    = num_sims//batch_size
        self.numFrames     = num_frames
        self.numSteps      = num_frames
        
        # initialize directory keys (using naming scheme from SoL codebase)
        # constant additional per-sim channel: Reynolds numbers from data generation
        # hard coded for training and test data here
        if not is_testset:
            self.dataSims = ['karman-fdt-hires-set/sim_%06d'%i for i in range(num_sims) ]
            ReNrs = [160000.0, 320000.0, 640000.0,  1280000.0,  2560000.0,  5120000.0]
            self.extConstChannelPerSim = { self.dataSims[i]:[ReNrs[i]] for i in range(num_sims) }
        else:
            self.dataSims = ['karman-fdt-hires-testset/sim_%06d'%i for i in range(num_sims) ]
            ReNrs = [120000.0, 480000.0, 1920000.0, 7680000.0] 
            self.extConstChannelPerSim = { self.dataSims[i]:[ReNrs[i]] for i in range(num_sims) }

        self.dataFrames = [ np.arange(num_frames) for _ in self.dataSims ]  

        # debugging example, check shape of a single marker density field:
        #print(format(self.dataPreloaded[self.dataSims[0]][0][0].shape )) 
        
        # the data has the following shape ['sim', frame, field (dens/vel)] where each field is [batch-size, y-size, x-size, channels]
        self.resolution = self.dataPreloaded[self.dataSims[0]][0][0].shape[1:3]  

        # compute data statistics for normalization
        self.dataStats = {
            'std': (
                np.std(np.concatenate([np.absolute(self.dataPreloaded[asim][i][0].reshape(-1)) for asim in self.dataSims for i in range(num_frames)], axis=-1)), # density
                np.std(np.concatenate([np.absolute(self.dataPreloaded[asim][i][1].reshape(-1)) for asim in self.dataSims for i in range(num_frames)], axis=-1)), # x-velocity
                np.std(np.concatenate([np.absolute(self.dataPreloaded[asim][i][2].reshape(-1)) for asim in self.dataSims for i in range(num_frames)], axis=-1)), # y-velocity
            )
        }
        self.dataStats.update({
            'ext.std': [ np.std([np.absolute(self.extConstChannelPerSim[asim][0]) for asim in self.dataSims]) ] # Reynolds Nr
        })

        
        if not is_testset:
            print("Data stats: "+format(self.dataStats))


    # re-shuffle data for next epoch
    def newEpoch(self, exclude_tail=0, shuffle_data=True):
        self.numSteps = self.numFrames - exclude_tail
        simSteps = [ (asim, self.dataFrames[i][0:(len(self.dataFrames[i])-exclude_tail)]) for i,asim in enumerate(self.dataSims) ]
        sim_step_pair = []
        for i,_ in enumerate(simSteps):
            sim_step_pair += [ (i, astep) for astep in simSteps[i][1] ]  # (sim_idx, step) ...

        if shuffle_data: random.shuffle(sim_step_pair)
        self.epoch = [ list(sim_step_pair[i*self.numSteps:(i+1)*self.numSteps]) for i in range(self.batchSize*self.numBatches) ]
        self.epochIdx += 1
        self.batchIdx = 0
        self.stepIdx = 0

    def nextBatch(self):  
        self.batchIdx += self.batchSize
        self.stepIdx = 0

    def nextStep(self):
        self.stepIdx += 1

在训练时，nextEpoch、nextBatch和nextStep函数将被调用以随机化训练数据的顺序。

现在我们需要一个编译小批量数据以进行训练的函数，称为下面的getData。它以标记密度、速度和雷诺数的形式返回所需大小的批次。

# for class Dataset():
def getData(self, consecutive_frames):
    d_hi = [
        np.concatenate([
            self.dataPreloaded[
                self.dataSims[self.epoch[self.batchIdx+i][self.stepIdx][0]] # sim_key
            ][
                self.epoch[self.batchIdx+i][self.stepIdx][1]+j # frames
            ][0]
            for i in range(self.batchSize)
        ], axis=0) for j in range(consecutive_frames+1)
    ]
    u_hi = [
        np.concatenate([
            self.dataPreloaded[
                self.dataSims[self.epoch[self.batchIdx+i][self.stepIdx][0]] # sim_key
            ][
                self.epoch[self.batchIdx+i][self.stepIdx][1]+j # frames
            ][1]
            for i in range(self.batchSize)
        ], axis=0) for j in range(consecutive_frames+1)
    ]
    v_hi = [
        np.concatenate([
            self.dataPreloaded[
                self.dataSims[self.epoch[self.batchIdx+i][self.stepIdx][0]] # sim_key
            ][
                self.epoch[self.batchIdx+i][self.stepIdx][1]+j # frames
            ][2]
            for i in range(self.batchSize)
        ], axis=0) for j in range(consecutive_frames+1)
    ]
    ext = [
        self.extConstChannelPerSim[
            self.dataSims[self.epoch[self.batchIdx+i][self.stepIdx][0]]
        ][0] for i in range(self.batchSize)
    ]
    return [d_hi, u_hi, v_hi, ext]

请注意，这里的density指的是被动传递的标记场，而不是流体的密度。下面我们将仅关注速度，标记密度仅用于可视化目的进行跟踪。

在所有定义完成后，我们最终可以运行一些代码。我们使用第一个单元格下载的数据定义dataset对象。

nsims = 6
batch_size = 3
simsteps = 500

dataset = Dataset( data_preloaded=data_preloaded, num_frames=simsteps, num_sims=nsims, batch_size=batch_size )

程序输出：

Data stats: {'std': (2.6542656, 0.23155601, 0.3066732), 'ext.std': [1732512.6262166172]}

此外，我们定义了几个全局变量来控制下一个代码单元格中的训练和模拟。

其中最重要和有趣的是msteps。它定义了在每个训练迭代中展开的模拟步数。这直接影响每个训练步骤的运行时间，因为我们首先必须模拟所有步骤，然后通过所有与NN评估交替的msteps模拟步骤反向传播梯度。然而，这是我们将在梯度方面收到重要反馈的地方，了解推断校正实际上如何影响运行中的模拟。因此，较大的msteps通常更好。

此外，我们在source_res中定义了模拟的分辨率，并分配了名为simulator的流体求解器对象。为了创建网格，它需要访问一个Domain对象，这个对象主要是为了方便而存在：它存储了域的分辨率、物理大小和边界条件。这些信息需要传递给每个网格，因此将其以Domain的形式放在一个地方是很方便的。对于上述设置，我们需要沿x和y方向有不同的边界条件：封闭壁面和自由流进出域。

我们还在下一个单元格中实例化了实际的NN network。

# one of the most crucial parameters: how many simulation steps to look into the future while training
msteps = 4

# # this is the actual resolution in terms of cells
source_res = list(dataset.resolution)
# # this is a virtual size, in terms of abstract units for the bounding box of the domain (it's important for conversions or when rescaling to physical units)
simulation_length = 100.

# for readability
from phi.physics._boundaries import Domain, OPEN, STICKY as CLOSED

boundary_conditions = {
    'y':(phi.physics._boundaries.OPEN,  phi.physics._boundaries.OPEN) ,
    'x':(phi.physics._boundaries.STICKY,phi.physics._boundaries.STICKY) 
}

domain = phi.physics._boundaries.Domain(y=source_res[0], x=source_res[1], boundaries=boundary_conditions, bounds=Box(y=2*simulation_length, x=simulation_length))
simulator = KarmanFlow(domain=domain)

network = network_small(dict(shape=(source_res[0],source_res[1], 3)))
network.summary()

输出为：

Model: "model"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 input_1 (InputLayer)        [(None, 64, 32, 3)]       0      
 conv2d (Conv2D)             (None, 64, 32, 32)        2432      
 leaky_re_lu (LeakyReLU)     (None, 64, 32, 32)        0         
 conv2d_1 (Conv2D)           (None, 64, 32, 32)        25632     
 leaky_re_lu_1 (LeakyReLU)   (None, 64, 32, 32)        0         
 conv2d_2 (Conv2D)           (None, 64, 32, 32)        25632     
 leaky_re_lu_2 (LeakyReLU)   (None, 64, 32, 32)        0         
 conv2d_3 (Conv2D)           (None, 64, 32, 2)         1602      
=================================================================
Total params: 55,298
Trainable params: 55,298
Non-trainable params: 0
_________________________________________________________________

12.6 交错模拟和神经网络

现在是整个设置中最关键的一步：我们定义一个函数，将模拟步骤和每个训练步骤中的网络评估封装起来。在定义辅助函数的所有工作之后，实际上很简单：我们通过tf.GradientTape()创建一个梯度磁带，以便稍后进行反向传播。然后，我们循环msteps，通过输入状态调用模拟器simulator.step，然后通过network(to_keras(...))评估校正。然后将NN校正添加到prediction列表中的最后一个模拟状态中（实际上我们只是用prediction[-1][1] + correction[-1]覆盖了最后一个模拟速度prediction[-1][1]）。

这里发生的另一件重要的事情是归一化：网络的输入被除以dataset.dataStats中的标准差。在评估network之后，我们只剩下一个速度，因此我们只需将其乘以速度的标准差（通过* dataset.dataStats['std'][1]和[2]）即可。

training_step函数还直接评估并返回损失。在这里，我们只是在整个序列上使用$L^2$损失，即迭代msteps。这需要一些代码行，因为我们分别循环“x”和“y”分量，以便将其归一化并与来自训练数据集的基准真值进行比较。

“学习”发生在最后两行中，通过tape.gradient()和opt.apply_gradients()，然后包含有关如何更改NN权重以将模拟推向完整模拟步骤的参考的聚合信息。

def training_step(dens_gt, vel_gt, Re, i_step):
    with tf.GradientTape() as tape:
        prediction, correction = [ [dens_gt[0],vel_gt[0]] ], [0] # predicted states with correction, inferred velocity corrections

        for i in range(msteps):
            prediction += [
                simulator.step(
                    density_in=prediction[-1][0],
                    velocity_in=prediction[-1][1],
                    re=Re, res=source_res[1],
                )
            ]       # prediction: [[density1, velocity1], [density2, velocity2], ...]

            model_input = to_keras(prediction[-1], Re)
            model_input /= math.tensor([dataset.dataStats['std'][1], dataset.dataStats['std'][2], dataset.dataStats['ext.std'][0]], channel('channels')) # [u, v, Re]
            model_out = network(model_input.native(['batch', 'y', 'x', 'channels']), training=True)
            model_out *= [dataset.dataStats['std'][1], dataset.dataStats['std'][2]] # [u, v]
            correction += [ to_phiflow(model_out, domain) ]                         # [velocity_correction1, velocity_correction2, ...]

            prediction[-1][1] = prediction[-1][1] + correction[-1]
 
        # evaluate loss
        loss_steps_x = [
            tf.nn.l2_loss(
                (
                    vel_gt[i].vector['x'].values.native(('batch', 'y', 'x'))
                    - prediction[i][1].vector['x'].values.native(('batch', 'y', 'x'))
                )/dataset.dataStats['std'][1]
            )
            for i in range(1,msteps+1)
        ]
        loss_steps_x_sum = tf.math.reduce_sum(loss_steps_x)

        loss_steps_y = [
            tf.nn.l2_loss(
                (
                    vel_gt[i].vector['y'].values.native(('batch', 'y', 'x'))
                    - prediction[i][1].vector['y'].values.native(('batch', 'y', 'x'))
                )/dataset.dataStats['std'][2]
            )
            for i in range(1,msteps+1)
        ]
        loss_steps_y_sum = tf.math.reduce_sum(loss_steps_y)

        loss = (loss_steps_x_sum + loss_steps_y_sum)/msteps

        gradients = tape.gradient(loss, network.trainable_variables)
        opt.apply_gradients(zip(gradients, network.trainable_variables))

        return math.tensor(loss)    

一旦定义了该函数，我们通过调用phiflow的math.jit_compile()函数来准备执行训练步骤。它会自动映射到所选后端的正确预编译步骤。例如，对于TF，它内部创建了一个计算图，并优化了操作链。对于JAX，它甚至可以编译优化的GPU代码（如果JAX设置正确）。因此，使用jit编译在运行时方面可以产生巨大的差异。

training_step_jit = math.jit_compile(training_step)

12.7 训练

为了训练，我们使用标准的Adam优化器，默认情况下运行5个时期。这是为了保持运行时间较短而选择的相对较低的数字。如果您有资源，进行10或15个时期将产生更准确的结果。对于更长时间的训练和更大的网络，降低学习率也将有益于时期的过程，但为了简单起见，我们将在这里保持LR为常数。

可选地，这也是加载网络状态以恢复训练的正确时机。

LR = 1e-4
EPOCHS = 5

opt = tf.keras.optimizers.Adam(learning_rate=LR) 

# optional, load existing network...
# set to epoch nr. to load existing network from there
resume = 0
if resume>0: 
    ld_network = keras.models.load_model('./nn_epoch{:04d}.h5'.format(resume)) 
    #ld_network = keras.models.load_model('./nn_final.h5') # or the last one
    network.set_weights(ld_network.get_weights())
    

最终，我们可以开始训练神经网络了！现在非常简单，我们只需循环所需的迭代次数，每次通过getData获取一个批次，将其馈入源模拟输入source_in，并在损失中与批次的reference数据进行比较。

上述设置将自动处理此处使用的可微分物理求解器提供正确的梯度信息，并将其提供给tensorflow网络。请注意：由于设置的复杂性，此次训练可能需要一段时间...(如果您有来自之前运行的保存的nn_final.h5网络，您可以潜在地跳过此块并通过上面的单元格加载先前训练过的模型。)

steps = 0
for j in range(EPOCHS):  # training
    dataset.newEpoch(exclude_tail=msteps)
    if j<resume:
        print('resume: skipping {} epoch'.format(j+1))
        steps += dataset.numSteps*dataset.numBatches
        continue

    for ib in range(dataset.numBatches):   
        for i in range(dataset.numSteps): 

            # batch: [[dens0, dens1, ...], [x-velo0, x-velo1, ...], [y-velo0, y-velo1, ...], [ReynoldsNr(s)]]            
            batch = getData(dataset, consecutive_frames=msteps)
            
            dens_gt = [   # [density0:CenteredGrid, density1, ...]
                domain.scalar_grid(
                    math.tensor(batch[0][k], math.batch('batch'), math.spatial('y, x')) 
                ) for k in range(msteps+1)
            ]

            vel_gt = [   # [velocity0:StaggeredGrid, velocity1, ...]
                domain.staggered_grid(
                    math.stack(
                        [
                            math.tensor(batch[2][k], math.batch('batch'), math.spatial('y, x')),
                            math.tensor(batch[1][k], math.batch('batch'), math.spatial('y, x')),
                        ], math.channel(vector="y,x")
                    ) 
                ) for k in range(msteps+1)
            ]
            re_nr = math.tensor(batch[3], math.batch('batch'))

            loss = training_step_jit(dens_gt, vel_gt, re_nr, math.tensor(steps)) 
            
            steps += 1
            if (j==0 and ib==0 and i<3) or (j==0 and ib==0 and i%128==0) or (j>0 and ib==0 and i==400): # reduce output 
              print('epoch {:03d}/{:03d}, batch {:03d}/{:03d}, step {:04d}/{:04d}: loss={}'.format( j+1, EPOCHS, ib+1, dataset.numBatches, i+1, dataset.numSteps, loss ))
            
            dataset.nextStep()

        dataset.nextBatch()

    if j%10==9: network.save('./nn_epoch{:04d}.h5'.format(j+1))

# all done! save final version
network.save('./nn_final.h5'); print("Training done, saved NN")

运行结果：

epoch 001/005, batch 001/002, step 0001/0496: loss=2565.1914
epoch 001/005, batch 001/002, step 0002/0496: loss=1434.6736
epoch 001/005, batch 001/002, step 0003/0496: loss=724.7997
epoch 001/005, batch 001/002, step 0129/0496: loss=40.198242
epoch 001/005, batch 001/002, step 0257/0496: loss=28.450535
epoch 001/005, batch 001/002, step 0385/0496: loss=27.100056
epoch 002/005, batch 001/002, step 0401/0496: loss=8.376183
epoch 003/005, batch 001/002, step 0401/0496: loss=4.7433133
epoch 004/005, batch 001/002, step 0401/0496: loss=4.522671
epoch 005/005, batch 001/002, step 0401/0496: loss=2.0179803
Training done, saved NN

损失应该从最初的1000以上下降到10以下。这是一个好的迹象，但当然更重要的是看NN-solver组合在新输入上的表现如何。通过这种培训方法，我们实现了一个混合求解器，由一个常规的“源”模拟器和一个经过训练以与此模拟器特定交互的网络组成，适用于所选的模拟案例领域。

让我们看看将其应用于一组新雷诺数的测试数据输入时，它的表现如何。

为了使事情保持简单，我们不会追求高性能版本的混合求解器。有关性能，请查看外部代码库：这里训练的网络应该直接可用于此应用脚本中。

12.8 评估

为了评估我们基于深度学习的求解器的性能，我们基本上只需要在每个训练迭代的内部循环中重复更多步骤。虽然在训练时我们受限于 msteps 次评估，但现在我们可以运行我们的求解器以任意长度。这是一个很好的测试，用于检验我们的求解器学习如何将数据保持在所需的分布中，并代表了更长回放的泛化测试。

我们重复使用上面的求解器代码，但在接下来，我们将考虑两个模拟版本：为了比较，我们将在“源”空间（即没有任何修改）中运行一个参考模拟。这个版本接收模拟器每次评估的常规输出，并忽略学习到的校正（存储在下面的 steps_source 中）。第二个版本是重复计算源求解器加上学习到的校正，并在求解器中推进这个状态（steps_hybrid）。

我们还需要一组新数据。下面，我们将下载一组新的雷诺数（在用于训练的雷诺数之间），在这些雷诺数上我们将运行未修改的模拟器和基于深度学习的模拟器。

fname_test = 'sol-karman-2d-test.pickle'
if not os.path.isfile(fname_test):
  print("Downloading test data (38MB), this can take a moment the first time...")
  urllib.request.urlretrieve("https://physicsbaseddeeplearning.org/data/"+fname_test, fname_test)

with open(fname_test, 'rb') as f: data_test_preloaded = pickle.load(f)
print("Loaded test data, {} training sims".format(len(data_test_preloaded)) )

输出：

Downloading test data (38MB), this can take a moment the first time...
Loaded test data, 4 training sims

接下来，我们创建一个新的数据集对象dataset_test，以组织数据。我们只是使用未打乱的数据集的第一个批次。

然而，有一个微妙但重要的问题：我们仍然必须使用原始训练数据集的标准化：dataset.dataStats['std']值。测试数据集有它自己的均值和标准差，因此训练过的神经网络从未见过这些数据。神经网络是使用上面的dataset中的数据进行训练的，因此我们必须使用那里的常量进行标准化，以确保网络接收到能够与其训练的数据相关的值。

dataset_test = Dataset( data_preloaded=data_test_preloaded, is_testset=True, num_frames=simsteps, num_sims=4, batch_size=4 )

# we only need 1 batch with t=0 states to initialize the test simulations with
dataset_test.newEpoch(shuffle_data=False)
batch = getData(dataset_test, consecutive_frames=0) 

re_nr_test = math.tensor(batch[3], math.batch('batch')) # Reynolds numbers
print("Reynolds numbers in test data set: "+format(re_nr_test))

输出：

Reynolds numbers in test data set: (120000.000, 480000.000, 1920000.000, 7680000.000) along batch

接下来，我们构建一个math.tensor作为居中标记场的初始状态，并从测试集批次的下两个索引中构建一个交错网格。类似于上面的to_phiflow，我们使用phi.math.stack()将适当大小的两个场组合成一个交错网格。

source_dens_initial = math.tensor( batch[0][0], math.batch('batch'), math.spatial('y, x'))

source_vel_initial = domain.staggered_grid(phi.math.stack([
    math.tensor(batch[2][0], math.batch('batch'),math.spatial('y, x')),
    math.tensor(batch[1][0], math.batch('batch'),math.spatial('y, x'))], channel(vector="y,x")) )

现在我们首先为基准运行 120 步的源模拟:

source_dens_test, source_vel_test = source_dens_initial, source_vel_initial
steps_source = [[source_dens_test,source_vel_test]]
STEPS=100

# note - math.jit_compile() not useful for numpy solve... hence not necessary here
for i in range(STEPS):
    [source_dens_test,source_vel_test] = simulator.step(
        density_in=source_dens_test,
        velocity_in=source_vel_test,
        re=re_nr_test,
        res=source_res[1],
    )
    steps_source.append( [source_dens_test,source_vel_test] )

print("Source simulation steps "+format(len(steps_source)))

结果：

Source simulation steps 101

接下来，我们计算我们学习到的混合求解器的相应状态。在这里，我们紧密地遵循训练代码，但是现在没有任何梯度磁带或损失计算。我们仅对每个模拟状态进行前向传递来评估神经网络，以计算校正场：

source_dens_test, source_vel_test = source_dens_initial, source_vel_initial
steps_hybrid = [[source_dens_test,source_vel_test]]
        
for i in range(STEPS):
    [source_dens_test,source_vel_test] = simulator.step(
        density_in=source_dens_test,
        velocity_in=source_vel_test,
        re=math.tensor(re_nr_test),
        res=source_res[1],
    )
    model_input = to_keras([source_dens_test,source_vel_test], re_nr_test )
    model_input /= math.tensor([dataset.dataStats['std'][1], dataset.dataStats['std'][2], dataset.dataStats['ext.std'][0]], channel('channels')) # [u, v, Re]
    model_out = network(model_input.native(['batch', 'y', 'x', 'channels']), training=False)
    model_out *= [dataset.dataStats['std'][1], dataset.dataStats['std'][2]] # [u, v]
    correction =  to_phiflow(model_out, domain) 
    source_vel_test = source_vel_test + correction

    steps_hybrid.append( [source_dens_test, source_vel_test] )
    
print("Steps with hybrid solver "+format(len(steps_hybrid)))

Steps with hybrid solver 101

根据存储的状态，我们量化神经网络带来的改进，并可视化结果。在下面的单元格中，索引b选择四个测试模拟中的一个（默认为索引0，低于训练数据范围之外的最低Re），并计算所有时间步长上的累积平均绝对误差（MAE）。

import pylab
b = 0 # batch index for the following comparisons

errors_source, errors_pred = [], []
for index in range(STEPS):
  vx_ref = dataset_test.dataPreloaded[ dataset_test.dataSims[b] ][ index ][1][0,...]
  vy_ref = dataset_test.dataPreloaded[ dataset_test.dataSims[b] ][ index ][2][0,...]
  vxs = vx_ref - steps_source[index][1].values.vector[1].numpy('batch,y,x')[b,...]
  vxh = vx_ref - steps_hybrid[index][1].values.vector[1].numpy('batch,y,x')[b,...]
  vys = vy_ref - steps_source[index][1].values.vector[0].numpy('batch,y,x')[b,...] 
  vyh = vy_ref - steps_hybrid[index][1].values.vector[0].numpy('batch,y,x')[b,...] 
  errors_source.append(np.mean(np.abs(vxs)) + np.mean(np.abs(vys))) 
  errors_pred.append(np.mean(np.abs(vxh)) + np.mean(np.abs(vyh)))

fig = pylab.figure().gca()
pltx = np.linspace(0,STEPS-1,STEPS)
fig.plot(pltx, errors_source, lw=2, color='mediumblue', label='Source')  
fig.plot(pltx, errors_pred,   lw=2, color='green', label='Hybrid')
pylab.xlabel('Time step'); pylab.ylabel('Error'); fig.legend()

print("MAE for source: "+format(np.mean(errors_source)) +" , and hybrid: "+format(np.mean(errors_pred)) )

输出结果：

MAE for source: 0.12054027616977692 , and hybrid: 0.04435234144330025

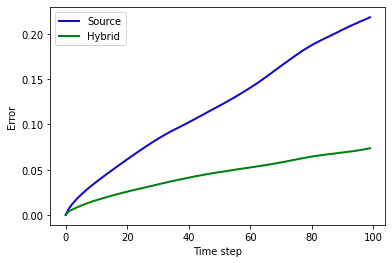
由于训练的复杂性, 性能各不相同, 但通常常规模拟的整体 MAE 约为混合模拟器的 2.5 倍。上图也显示了这种随时间的行为。通常甚至对于训练数据范围内的其他雷诺数,差距更大 (对上面的 b 尝试其他值)。

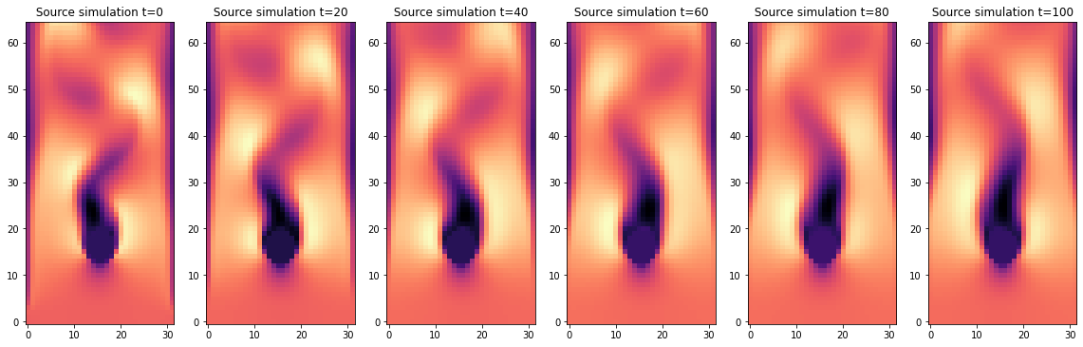
我们还通过绘制速度 y 分量随时间可视化两个输出的差异。以下两个代码单元显示了批处理索引 b 的六个速度快照, 以 20 个时间步长的间隔。

c = 0          # channel selector, x=1 or y=0 
interval = 20  # time interval
IMGS = STEPS//20+1

fig, axes = pylab.subplots(1, IMGS, figsize=(16, 5))    
for i in range(0,IMGS):
  v = steps_source[i*interval][1].values.vector[c].numpy('batch,y,x')[b,...]
  axes[i].imshow( v , origin='lower', cmap='magma')
  axes[i].set_title(f" Source simulation t={i*interval} ")

pylab.tight_layout()

fig, axes = pylab.subplots(1, IMGS, figsize=(16, 5))
for i in range(0,IMGS):
  v = steps_hybrid[i*interval][1].values.vector[c].numpy('batch,y,x')[b,...]
  axes[i].imshow( v , origin='lower', cmap='magma')
  axes[i].set_title(f" Hybrid solver t={i*interval} ")
pylab.tight_layout()

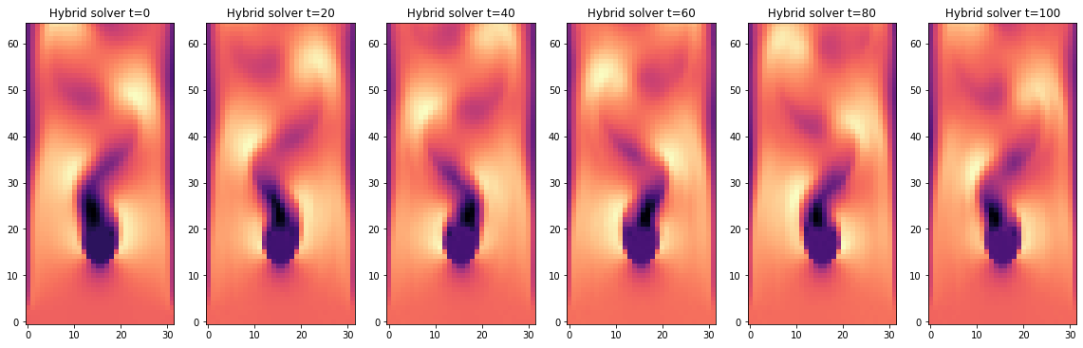
它们在$t=0$时都以相同的初始状态开始（参考解流形的下采样解），在$t=20$时，两个解仍然具有相似性。随着时间的推移，源版本强烈扩散了流动中的结构并失去了动量。障碍物后面的流动变得笔直，缺乏明显的涡旋。

混合求解器生成的版本要好得多。即使经过一百多次更新，它仍然保留了涡 shedding。请注意，这两个输出都是由相同的基础求解器生成的。第二个版本仅仅受益于学习到的修正器，它成功地恢复了源求解器的数值误差，包括其过度强的耗散。

我们还通过视觉比较NN相对于参考数据的表现。下一个单元格绘制了三个版本的一个时间步长：经过50步的参考数据，以及源和我们的混合求解器的重新模拟版本，以及两者的每个单元格误差。

index = STEPS//2 # time step index
vx_ref = dataset_test.dataPreloaded[ dataset_test.dataSims[b] ][ index ][1][0,...]
vx_src = steps_source[index][1].values.vector[1].numpy('batch,y,x')[b,...]
vx_hyb = steps_hybrid[index][1].values.vector[1].numpy('batch,y,x')[b,...]

fig, axes = pylab.subplots(1, 4, figsize=(14, 5))

axes[0].imshow( vx_ref , origin='lower', cmap='magma')
axes[0].set_title(f" Reference ")

axes[1].imshow( vx_src , origin='lower', cmap='magma')
axes[1].set_title(f" Source ")

axes[2].imshow( vx_hyb , origin='lower', cmap='magma')
axes[2].set_title(f" Learned ")

# show error side by side
err_source = vx_ref - vx_src 
err_hybrid = vx_ref - vx_hyb 
v = np.concatenate([err_source,err_hybrid], axis=1)
axes[3].imshow( v , origin='lower', cmap='cividis')
axes[3].set_title(f" Errors: Source & Learned")

pylab.tight_layout()

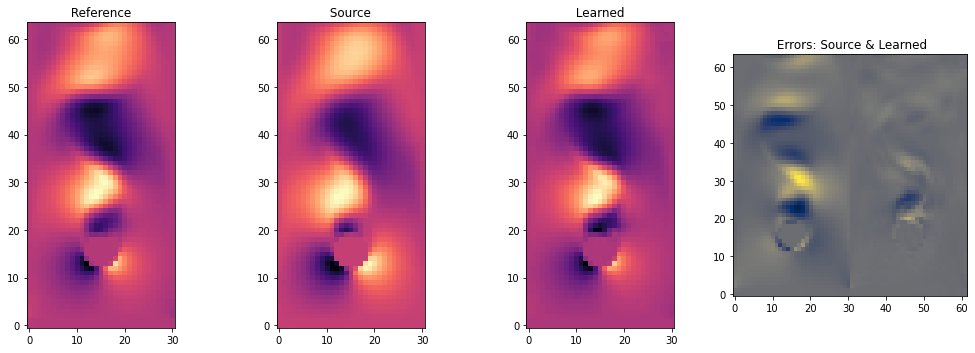
这清晰地展示了中间的纯源模拟与左侧参考解的偏差。学习版本与参考解的接近程度更高。

右侧的两个每单元误差图像也说明了这一点：源版本具有更大的误差（即更亮的颜色），显示它系统地低估了应该形成的涡旋。学习版本的误差分布更加均匀，且数量级显著较小。

本次评估到此结束。需要注意的是，混合求解器的改进行为往往难以通过简单的向量范数（如MAE或$L^2$范数）进行可靠的测量。为了改进这一点，我们需要采用其他特定领域的指标。在本例中，基于流动涡度和湍流特性的流体度量将是适用的。然而，在本文中，我们希望集中讨论与DL相关的主题，并在下一章中针对另一个可微物理求解器的反问题进行研究。

12.9 下一步

• 修改训练以进一步减少训练误差。使用中等规模的网络, 您应该能将损失降低到约 1。

• 关闭可微分物理训练 (通过设置 msteps=1), 并与 DP 版本进行比较。

• 类似地, 用更大的 msteps 设置训练网络, 例如 8 或 16。请注意, 由于训练的递归性质, 您可能需要加载预训练状态来稳定最初的迭代。

• 使用外部 github 代码生成新的测试数据, 并在这些用例上运行您的训练好的神经网络。您会发现, 降低训练误差不总是直接相关于改进的测试性能。