我们现在以Navier-Stokes方程作为物理模型来考虑一个更复杂的例子。根据 Navier-Stokes Forward Simulation，我们将考虑一个二维情况。

作为优化目标，我们将考虑前面Burgers方程例子的一个更困难的变体：观测到的密度 $s$ 在经过 $n = 20$ 步模拟后应与给定的目标匹配。与之前不同的是，以标记场 $s$ 的形式观测到的量不能以任何方式改变。只能修改 $t = 0$ 时速度 $u_{0}$ 的初始状态。这给了我们在损失函数表达中可观测量和在优化过程中（或之后通过神经网络）可以进行交互的量之间的分离。

10.1 物理模型

我们将使用无粘性Navier-Stokes模型，其中包含速度 $u$ ，没有显式的粘度项，并且有一个烟雾标记密度 $s$ ，它驱动一个简单的Boussinesq浮力项 $η d$ ，在y维度上添加一个力。由于缺乏显式粘度，这些方程等价于欧拉方程。因此，我们得到： $\frac{\partial u _{x}}{\partial t} + u \cdot \nabla u_{x} \frac{\partial u _{y}}{\partial t} + u \cdot \nabla u_{y} s.t. \nabla \cdot u = - \frac{1}{ρ} \nabla p = - \frac{1}{ρ} \nabla p + η d = 0 ，$

以及被动运移标记密度 $s$ 的额外的输运方程:

$\frac{\partial s}{\partial t} + u \cdot \nabla s = 0$

10.2 形式化

使用2 概述中的符号表示法，上述逆问题可以表述为最小化问题

$arg min_{u_{0}} i \sum (f (x_{t_{e} ， i}; u_{0}) - y_{t_{e} ， i}^{*})^{2} ，$

在目标时间 $t_{e}$ 处， $y_{t_{e}, i}^{*}$ 是参考解的样本，而 $x_{t_{e}, i}$ 表示我们模拟器在相同采样位置和时间的估计值。这里的索引 $i$ 遍历流体求解器中所有离散化的空间自由度（下面我们将使用 $32 \times 40$ ）。

与以前不同的是，我们不再处理预先计算的数量，而是现在 $x_{t_{e}, i}$ 本身是一个复杂的非线性函数。更具体地说，模拟器从初始速度 $u_{0}$ 和密度 $s_{0}$ 开始，通过对离散化的PDE $P$ 进行 $n$ 次评估来计算 $x_{t_{e}, i}$ 。这给出了模拟的最终状态 $y_{t_{e}, i} = s_{t_{e}} = P^{n} (u_{0}, s_{0})$ ，在接下来的过程中，我们将保持 $s_{0}$ 不变，将重点放在 $u_{0}$ 上作为我们的自由度。

因此，优化只能改变 $u_{0}$ 以尽可能准确地使 $y_{t_{e} ， i}$ 与参考值 $y_{t_{e} ， i}^{*}$ 对齐。

10.3 开始实现

首先，让我们先处理Python模块的加载。通过导入phi.torch.flow，我们可以获得在PyTorch中工作并能够提供梯度的流体模拟函数（对于TensorFlow，可以选择使用phi.tf.flow）。

!pip install --upgrade --quiet phiflow==2.2
from phi.torch.flow import *  
import pylab # for visualizations later on

10.4 批量模拟

现在我们可以设置模拟，该模拟将与之前的“常规”模拟示例（来自{doc}overview-ns-forw）保持一致。然而，现在我们将直接包含一个额外的维度，类似于用于神经网络训练的小批量。为此，我们将引入一个名为inflow_loc的命名维度。这个维度将存在于之前的空间维度y、x之上，这些维度被声明为vector通道的维度。正如inflow_loc这个名字所示，这个维度的主要区别在于入流的不同位置，以获得不同的流动模拟。在phiflow中的命名维度使得在不同张量的匹配维度之间广播信息非常方便。

# closed domain
INFLOW_LOCATION = tensor([(12, 4), (13, 6), (14, 5), (16, 5)], batch('inflow_loc'), channel(vector="x,y"))
INFLOW = (1./3.) * CenteredGrid(Sphere(center=INFLOW_LOCATION, radius=3), extrapolation.BOUNDARY, x=32, y=40, bounds=Box(x=(0,32), y=(0,40)))
BND = extrapolation.ZERO # closed, boundary conditions for velocity grid below

# uncomment this for a slightly different open domain case
#INFLOW_LOCATION = tensor([(11, 6), (12, 4), (14, 5), (16, 5)], batch('inflow_loc'), channel(vector="x,y"))
#INFLOW = (1./4.) * CenteredGrid(Sphere(center=INFLOW_LOCATION, radius=3), extrapolation.BOUNDARY, x=32, y=40, bounds=Box(x=(0,32), y=(0,40)))
#BND = extrapolation.BOUNDARY # open boundaries 

INFLOW.shape

输出结果：

(inflow_locᵇ=4, xˢ=32, yˢ=40)

最后一条语句验证我们的 INFLOW 网格同样具有 inflow_loc 维度，以及空间维度 x 和 y。您可以在 phiflow 中使用 .exists 布尔值来测试张量维度的存在。例如，上述 INFLOW.inflow_loc.exists 将给出 True，而 INFLOW.some_unknown_dim.exists 将给出 False。上标 $^{b}$ 表示 inflow_loc 是一个批量维度。

Phiflow 张量会通过其名称自动广播到新维度，因此通常不需要重新塑形操作。例如，您可以轻松添加或乘以具有不同维度的张量。在下面，我们将一个交错网格与沿 inflow_loc 维度的全 1 张量相乘，通过 StaggeredGrid(...) * math.ones(batch(inflow_loc=4)) 得到一个具有 x，y，inflow_loc 作为维度的交错速度场。

现在我们可以轻松地从这些不同的初始条件模拟几步。由于广播，我们在概述章节中用于单前向模拟的完全相同的代码将产生四个模拟，具有不同的烟雾进流位置。

smoke = CenteredGrid(0, extrapolation.BOUNDARY, x=32, y=40, bounds=Box(x=(0,32), y=(0,40)))  # sampled at cell centers
velocity = StaggeredGrid(0, BND, x=32, y=40, bounds=Box(x=(0,32), y=(0,40)))  # sampled in staggered form at face centers 

def step(smoke, velocity):
  smoke = advect.mac_cormack(smoke, velocity, dt=1) + INFLOW
  buoyancy_force = (smoke * (0, 1)).at(velocity)
  velocity = advect.semi_lagrangian(velocity, velocity, dt=1) + buoyancy_force
  velocity, _ = fluid.make_incompressible(velocity)
  return smoke, velocity

for _ in range(20):
    smoke,velocity = step(smoke,velocity)

# store and show final states (before optimization)
smoke_final = smoke 
fig, axes = pylab.subplots(1, 4, figsize=(10, 6))
for i in range(INFLOW.shape.get_size('inflow_loc')):
  axes[i].imshow(smoke_final.values.numpy('inflow_loc,y,x')[i,...], origin='lower', cmap='magma')
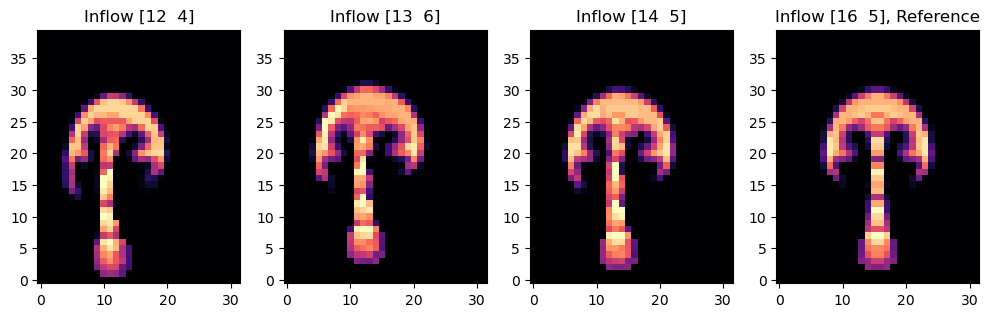
  axes[i].set_title(f"Inflow {INFLOW_LOCATION.numpy('inflow_loc,vector')[i]}" + (", Reference" if i==3 else ""))
pylab.tight_layout()

注：这里若报告“OMP: Error #15: Initializing libiomp5md.dll, but found libiomp5md.dll already initialized.”错误，可在最前面指定环境变量：import os os.environ['KMP_DUPLICATE_LIB_OK']='True'

最后一张图展示了经过20步模拟后，流场中烟雾的状态。模拟[3]中的最终烟雾形状，在右侧有一个直立的烟囱，将作为我们下面的参考状态。其他三个模拟的初始速度将在下面的优化过程中进行修改，以匹配这个参考状态。

（作为一个小的附注：phiflow张量将使用它们创建时的后端来跟踪它们的操作链。例如，使用NumPy创建的张量将继续使用NumPy/SciPy的操作，除非同时传递给相同操作的PyTorch或TensorFlow张量。因此，定期验证张量是否使用了正确的后端是一个好主意，例如通过GRID.values.default_backend。）

梯度

让我们看看如何从我们的模拟中获取梯度。上面已经处理的第一个简单的步骤是包含 phi.torch.flow 来导入可微分算子以构建我们的模拟器。

现在我们想要优化初始速度，使得所有模拟都到达一个类似于右侧模拟的最终状态，其中入口位于 (16, 5)，即沿 x 居中。为了实现这一点，我们在模拟过程中记录梯度，并定义一个简单的基于 $L^{2}$ 的损失函数。我们将使用的损失函数由 $L = ∣ s_{t_{e}} - s_{t_{e}}^{*} ∣^{2}$ 给出，其中 $s_{t_{e}}$ 表示烟密度， $s_{t_{e}}^{*}$ 表示我们批处理中第四个模拟的参考状态（均在最后时间步 $t_{e}$ 评估）。在评估损失函数时，我们将参考状态视为外部常量，通过 field.stop_gradient() 处理。正如上面所述， $s$ 是 $u$ 的函数（通过平流方程），而 $u$ 又由 Navier-Stokes 方程给出。因此，通过多个时间步的链式关系， $s$ 取决于初始速度状态 $u_{0}$ 。

重要的是，在记录梯度之前，我们的初始速度具有 inflow_loc 维度，以便我们具有完整的速度“小批量”（其中三个将在后续优化中通过梯度更新）。为了获得适当的速度张量，我们使用零张量初始化一个 StaggeredGrid，沿着 inflow_loc 批处理维度。由于交错网格已经具有 y,x 和 vector 维度，因此这给出了所需的四个维度，如下面的打印语句所验证的。

Phiflow 通过使用需要返回损失值以及可选状态值的函数，在不同平台上提供了统一的梯度 API。它使用基于损失函数的接口，我们在下面定义了 simulate 函数。simulate 计算上述 $L^{2}$ 误差，并在 20 个模拟步骤后返回演化的 smoke 和 velocity 状态。

initial_smoke = CenteredGrid(0, extrapolation.BOUNDARY, x=32, y=40, bounds=Box(x=(0,32), y=(0,40)))
initial_velocity = StaggeredGrid(math.zeros(batch(inflow_loc=4)), BND, x=32, y=40, bounds=Box(x=(0,32), y=(0,40)))
print("Velocity dimensions: "+format(initial_velocity.shape))

def simulate(smoke: CenteredGrid, velocity: StaggeredGrid):
    for _ in range(20):
        smoke,velocity = step(smoke,velocity)
        
    loss = field.l2_loss(smoke - field.stop_gradient(smoke.inflow_loc[-1]) )
    # optionally, use smoother loss with diffusion steps - no difference here, but can be useful for more complex cases
    #loss = field.l2_loss(diffuse.explicit(smoke - field.stop_gradient(smoke.inflow_loc[-1]), 1, 1, 10))
    
    return loss, smoke, velocity

输出结果：

Velocity dimensions: (inflow_locᵇ=4, xˢ=32, yˢ=40, vectorᶜ=x,y)

Phiflow的field.functional_gradient()函数是计算梯度的核心函数。接下来，我们将使用它来获取相对于初始速度的梯度。由于速度是simulate()函数的第二个参数，我们传递wrt=[1]。（Phiflow还有一个field.spatial_gradient函数，它计算张量沿空间维度（如x，y）的导数。）

functional_gradient生成一个梯度函数。作为演示，下一个单元格使用烟雾和速度的初始状态评估梯度一次。最后一条语句打印了结果梯度张量的部分摘要。

sim_grad = field.functional_gradient(simulate, wrt=[1], get_output=False)
(velocity_grad,) = sim_grad(initial_smoke, initial_velocity)

print("Some gradient info: " + format(velocity_grad))
print(format(velocity_grad.values.inflow_loc[0].vector[0])) # one example, location 0, x component, automatically prints size & content range

输出结果：

Some gradient info: StaggeredGrid[(inflow_locᵇ=4, xˢ=32, yˢ=40, vectorᶜ=x,y), size=(x=32, y=40) int64, extrapolation=0]
(xˢ=31, yˢ=40) 2.61e-08 ± 8.5e-01 (-2e+01...1e+01)

最后两行代码只是打印了一些关于生成的梯度场的信息。自然地，它的形状与速度本身相同：它是一个带有四个流入位置的交错网格。最后一行展示了如何访问其中一个梯度的x分量。

我们可以使用常规的绘图函数来查看计算得到的梯度的内容，例如，通过将其中一个模拟的x分量转换为numpy数组，使用velocity_grad.values.inflow_loc[0].vector[0].numpy('y,x')。另一种交互式的选择是使用phiflow的view()函数，它会自动分析网格内容并提供UI按钮来选择不同的查看模式。您可以使用它们来显示箭头、二维速度向量的单个分量或者它们的大小。由于它的交互性质，对应的图像不会在Jupyter之外显示，因此我们通过plot()来显示下面的向量长度。

# neat phiflow helper function:
vis.plot(field.vec_length(velocity_grad)) # show magnitude

输出结果：

<Figure size 864x360 with 5 Axes>

毫不奇怪，左侧的第四个梯度为零（它已经与参考值相匹配）。其他三个梯度已检测到初始回流位置的变化，表现为围绕回流的圆形形状的正负区域。左侧较大距离的梯度也明显更大。

优化

上面可视化的梯度只是指向增加损失的线性化变化。现在我们可以通过更新初始速度的相反方向来最小化损失，并迭代寻找最小值。

这是一个困难的任务：由于不同的初始空间密度配置，模拟产生了不同的动力学。我们的优化现在应该找到一个单一的初始速度状态，使得在 $t = 20$ 时与参考模拟具有相同的状态。因此，在进行20个非线性更新步骤后，模拟应该能够再现所需的标记密度状态。要达到这个目标，只需改变标记流入的位置会更容易，但为了使事情更困难和有趣，流入不是自由度。优化器只能改变初始速度 $u_{0}$ 。

下面的单元格实现了一个简单的最陡梯度下降优化：重新评估梯度函数，并迭代多次以使用学习率（步长）LR优化 $u_{0}$ 。

field.functional_gradient有一个参数get_output，确定是否返回函数的原始结果（在我们的例子中为simulate()）或仅返回梯度。由于追踪损失在迭代过程中的演变是有趣的，让我们重新定义带有get_output=True的梯度函数。

sim_grad_wloss = field.functional_gradient(simulate, wrt=[1], get_output=True) # if we need outputs...

LR = 1e-03 
for optim_step in range(80):    
    (loss, _smoke, _velocity), (velocity_grad,) = sim_grad_wloss(initial_smoke, initial_velocity)
    initial_velocity = initial_velocity - LR * velocity_grad
    if optim_step<3 or optim_step%10==9: print('Optimization step %d, loss: %f' % (optim_step, np.sum(loss.numpy()) ))

输出：

Optimization step 0, loss: 298.286163
Optimization step 1, loss: 291.454102
Optimization step 2, loss: 276.057861
Optimization step 9, loss: 235.939117
Optimization step 19, loss: 211.866379
Optimization step 29, loss: 186.080994
Optimization step 39, loss: 170.441772
Optimization step 49, loss: 181.928848
Optimization step 59, loss: 181.899567
Optimization step 69, loss: 164.614792
Optimization step 79, loss: 161.756241

损失应该显著下降，从近300降至170以下，现在我们还可以可视化在优化中获得的初始速度。

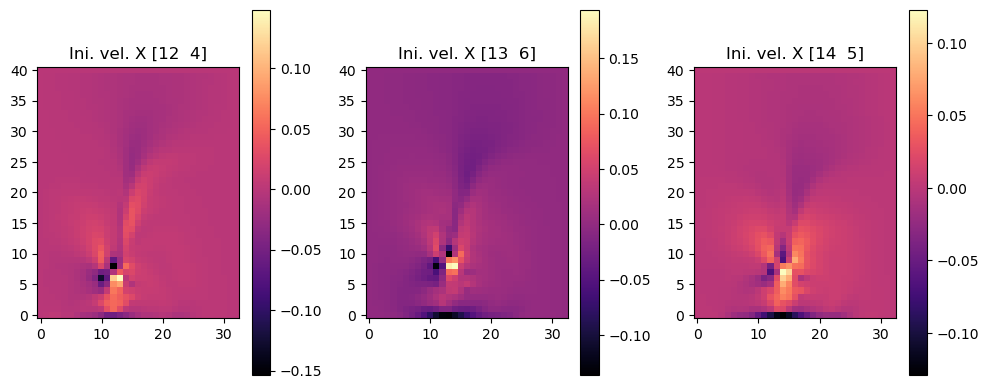
以下图像显示了三个初始速度的结果，分别是它们的x分量（第一组图像）和y分量（第二组图像）。我们跳过了第四组图像，即inflow_loc[0]，因为它只包含零。

fig, axes = pylab.subplots(1, 3, figsize=(10, 4))
for i in range(INFLOW.shape.get_size('inflow_loc')-1):
  im = axes[i].imshow(initial_velocity.staggered_tensor().numpy('inflow_loc,y,x,vector')[i,...,0], origin='lower', cmap='magma')
  axes[i].set_title(f"Ini. vel. X {INFLOW_LOCATION.numpy('inflow_loc,vector')[i]}")
  pylab.colorbar(im,ax=axes[i])
pylab.tight_layout()

fig, axes = pylab.subplots(1, 3, figsize=(10, 4))
for i in range(INFLOW.shape.get_size('inflow_loc')-1):
  im = axes[i].imshow(initial_velocity.staggered_tensor().numpy('inflow_loc,y,x,vector')[i,...,1], origin='lower', cmap='magma')
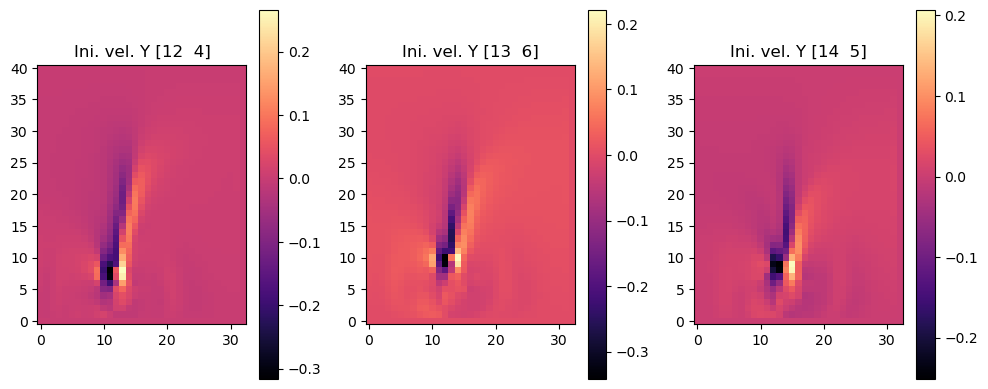
  axes[i].set_title(f"Ini. vel. Y {INFLOW_LOCATION.numpy('inflow_loc,vector')[i]}")
  pylab.colorbar(im,ax=axes[i])
pylab.tight_layout()

重新模拟

我们还可以可视化模拟在20步的完整过程，考虑到每个流入位置的新初始速度条件。这就是在每次梯度计算时优化过程内部发生的情况，也是我们的损失函数所测量的。因此，了解优化算法找到了哪些解是很有帮助的。

下面，我们使用initial_velocity中的新初始条件重新运行正向模拟：

smoke = initial_smoke 
velocity = initial_velocity

for _ in range(20):
    smoke,velocity = step(smoke,velocity)

fig, axes = pylab.subplots(1, 4, figsize=(10, 6))
for i in range(INFLOW.shape.get_size('inflow_loc')):
  axes[i].imshow(smoke_final.values.numpy('inflow_loc,y,x')[i,...], origin='lower', cmap='magma')
  axes[i].set_title(f"Inflow {INFLOW_LOCATION.numpy('inflow_loc,vector')[i]}" + (", Reference" if i==3 else ""))
pylab.tight_layout()

自然地，右边的图像是相同的（这是参考图像），而其他三个模拟现在向右偏移。由于差异有点微妙，让我们可视化目标配置与不同最终状态之间的差异。

以下图像显示了演化模拟和目标密度之间的差异。因此，暗区域表示目标应该出现但没有出现的地方。顶行显示了初始速度为零的原始状态，而底行显示了经过优化调整初始速度后的版本。因此，在每一列中，您可以比较之前（顶部）和之后（底部）的情况。

fig, axes = pylab.subplots(2, 3, figsize=(10, 6))
for i in range(INFLOW.shape.get_size('inflow_loc')-1):
  axes[0,i].imshow(smoke_final.values.numpy('inflow_loc,y,x')[i,...] - smoke_final.values.numpy('inflow_loc,y,x')[3,...], origin='lower', cmap='magma')
  axes[0,i].set_title(f"Org. diff. {INFLOW_LOCATION.numpy('inflow_loc,vector')[i]}")
  pylab.colorbar(im,ax=axes[0,i])
for i in range(INFLOW.shape.get_size('inflow_loc')-1):
  axes[1,i].imshow(smoke.values.numpy('inflow_loc,y,x')[i,...] - smoke_final.values.numpy('inflow_loc,y,x')[3,...], origin='lower', cmap='magma')
  axes[1,i].set_title(f"Result {INFLOW_LOCATION.numpy('inflow_loc,vector')[i]}")
  pylab.colorbar(im,ax=axes[1,i])

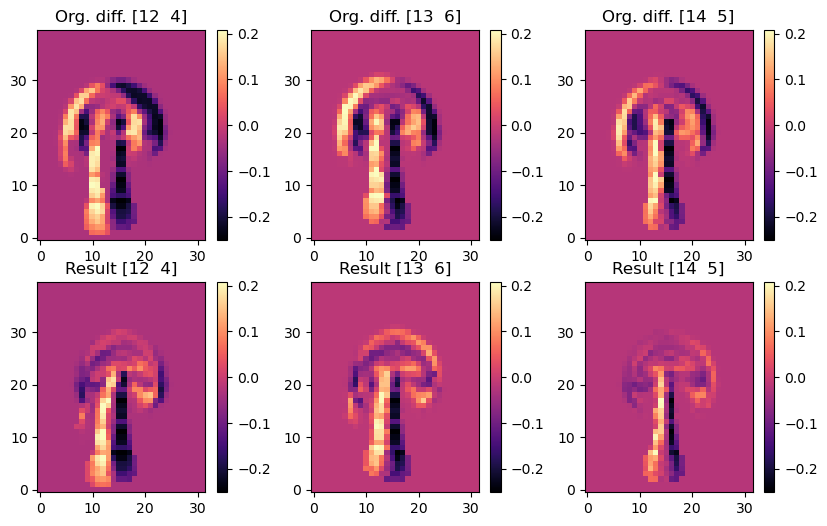
这些差异图清晰地显示出优化成功地对齐了烟羽的上部区域。每个原始图像（顶部）都显示出明显的不对齐，即黑色光晕，而优化后的状态在很大程度上与参考的目标烟雾配置重叠，并且在每个烟云的前部展示出更接近零的差异。

需要注意的是，所有三个模拟都需要与固定的流入进行“配合”，因此它们不能仅仅“凭空”产生标记密度以匹配目标。此外，每个模拟还需要考虑非线性模型方程如何在20个时间步骤内改变系统状态。因此，优化目标非常困难，在这种情况下，无法完全满足约束条件以匹配参考模拟。例如，这在烟羽的茎部是明显的，优化后仍然显示出黑色的光晕。优化无法改变流入位置，因此需要专注于对齐烟羽的上部区域。

结论

这个例子说明了可微分物理方法如何轻松地扩展到更加复杂的偏微分方程。如上所述，我们已经对一个完整的Navier-Stokes求解器进行了20个步骤的小批量优化。

这为将神经网络引入图像提供了强大的基础。正如你可能已经注意到的，我们的自由度仍然是一个常规的网格，并且我们共同解决了一个单一的反问题。当然，需要解决三个案例作为小批量，但尽管如此，这个设置仍然代表了一个直接的优化过程。因此，与{doc}physicalloss-code中的PINN示例一致，我们在这里并没有真正处理一个“机器学习”任务。然而，DP训练允许与神经网络进行各种灵活的组合，这将是下一章的主题。

下一步

基于上述的代码示例，我们可以推荐尝试以下实验：

修改模拟的设置，使其在四个实例之间的差异更加明显，运行时间更长，或者使用更细的空间离散化（即更大的网格尺寸）。请注意，这将使优化问题更加困难，因此可能无法通过这个简单的设置直接收敛。
作为一个更大的改变，添加多分辨率优化来处理具有更大差异的情况。即，首先使用粗糙的离散化求解，然后将此解作为更细的离散化的初始猜测。