可视化求解

可视化位移和应力的求解。

  1. 激活图形窗口中的位移场景。
  2. 单击 （保存-恢复-选择视图）并选择视图 > -X > 上 +Y。


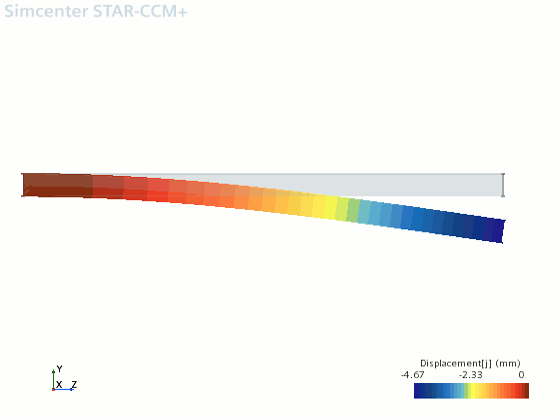
    计算的最大位移约为 4.67 mm。Bernoulli-Euler 梁理论预测位移大约为 4.63 mm，因此数值解决方案与理论结果差值小于 1%。

  3. 激活图形窗口中的应力场景。
  4. 单击 （保存-恢复-选择视图），并选择恢复视图 > 视图 1。


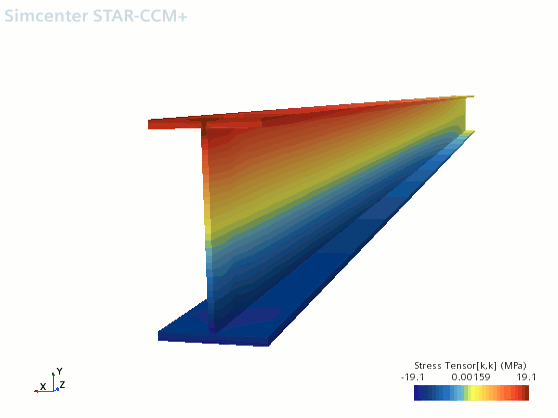
和预期一样，应力场景显示腹板末端的应力高度集中，此腹板在所有自由度上受到约束。检查顶凸缘角的应力，此凸缘角远离受约束区域：
  1. 右键单击报告 > 应力 [k,k] 节点，然后选择运行报告。
    报告打印至输出窗口。顶凸缘角的计算应力大约为 17.4 MPa，这与 Euler-Bernoulli 梁理论提供的值 17.3 MPa 十分一致。
为了可视化固定约束条件附近计算应力如何偏离 Euler-Bernoulli 梁理论：
  1. 右键单击报告 > 固定约束条件附近应力 [k,k] 节点，然后选择运行报告。
    报告打印至输出窗口。腹板上端点的计算应力大约为 18.61 MPa，这比 Euler-Bernoulli 梁理论给出的结果高。
下表总结了此分析的结果。第一行显示 Euler-Bernoulli 梁理论的分析求解。第二行报告此教程获得的数值求解。为了便于比较，第三行显示同时对凸缘和腹板应用固定约束条件时获得的数值求解。
求解法 位移 [j] σzz 在凸缘中心 σzz 在凸缘角
Euler-Bernoulli 梁理论 - 4.63 mm 17.34 MPa 17.34 MPa
Simcenter STAR-CCM+ 分析条件：
  • 腹板的固定约束条件
  • 凸缘的法向位移约束条件
 - 4.67 mm 18.61 MPa 17.42 MPa
Simcenter STAR-CCM+ 分析条件：
  • 腹板和凸缘的固定约束条件
 -4.66 mm 20.67 MPa 24.08 MPa