除冰

假设除冰是一个准稳态过程。

冰层在温度为 $T_{i c e}$ 时通过壁面热通量 $q$ 融化。其中，冰层吸收的热通量比例为 $C_{e m p}$ 。当冻结温度为 $T_{F}$ 时，已融化的冰将作为径流流走，它不能在当前模型中重新冻结。此过程相关的质量和能量通量如下图所示：

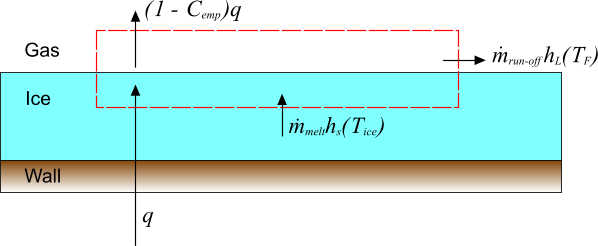
除冰过程的质量平衡很简单

图 1. EQUATION_DISPLAY

{\dot{m}}_{m e l t} = {\dot{m}}_{r u n - o f f}

(214)

由于假设径流无法重新冻结且存在额外约束 ${\dot{m}}_{r u n - o f f} \geq 0$ ，因此根据 Eqn. (214)， ${\dot{m}}_{m e l t} \geq 0$ 。

在此过程中，通过忽略与质量通量相关的动能，能量平衡为：

图 2. EQUATION_DISPLAY

{\dot{m}}_{m e l t} h_{s} (T_{i c e}) + q = {\dot{m}}_{r u n - o f f} h_{L} (T_{F}) + (1 - C_{e m p}) q

(215)

其中， $h_{s} (T_{i c e})$ 是冰层温度下固体冰的焓，而 $h_{L} (T_{F})$ 是冻结温度下与融冰相关的焓。这些焓通过以下公式与温度相关：

图 3. EQUATION_DISPLAY

h_{s} (T) = C_{p, s} T

(216)

图 4. EQUATION_DISPLAY

h_{L} (T) = C_{p, s} T + L

(217)

通过利用这些关系和质量平衡并重新排列，可以得出融化速率的显式表达式：

图 5. EQUATION_DISPLAY

{\dot{m}}_{m e l t} = \frac{C_{e m p} q}{C_{p, s} (T_{F} - T_{i c e}) + L}

(218)

必须对此方程强制施加约束 ${\dot{m}}_{m e l t} \geq 0$ 。如果 Eqn. (218) 预测 ${\dot{m}}_{m e l t}$ 为负，则将其剪切为零。

对于给定 ${\dot{m}}_{m e l t}$ ，可使用以下公式更新冰厚度 s：

图 6. EQUATION_DISPLAY

\frac{d s}{d t} = - \frac{{\dot{m}}_{m e l t}}{ρ_{s}}

(219)

其中 $ρ_{s}$ 是冰层的密度。

吸积

上述分析可进一步扩展，以包括液滴的额外入射质量通量，每个此类质量通量均具有质量 $m_{d}$ 、温度 $T_{d}$ 和速度 $v_{d}$ 。此表达式旨在表示碰撞到表面上的液滴。对总体能量平衡的各种影响如下所示：

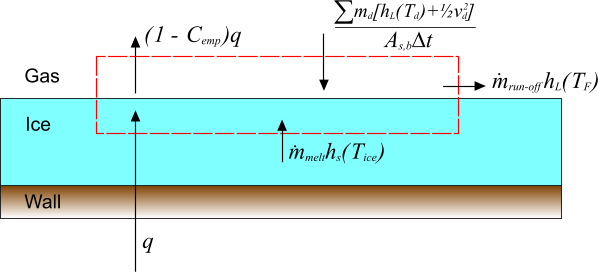
在上图中， $A_{s, b}$ 是液滴碰撞的边界面的表面积， $Δ t$ 为时间步。项：

$\frac{\sum_{}^{} m_{d} [h_{L} (T_{d}) + \frac{1}{2} v_{d}^{2}]}{A_{s, b} Δ t}$

指示因碰撞液滴产生的总体能量通量。

因此，质量平衡如下式所示：

图 7. EQUATION_DISPLAY

{\dot{m}}_{m e l t} + {\dot{m}}_{d} = {\dot{m}}_{r u n - o f f}

(220)

其中：

图 8. EQUATION_DISPLAY

{\dot{m}}_{d} = \frac{\sum_{}^{} m_{d}}{A_{s, b} Δ t}

(221)

除约束 ${\dot{m}}_{r u n - o f f} \geq 0$ 以外，还有 ${\dot{m}}_{d} \geq 0$ 。 ${\dot{m}}_{m e l t}$ 上的约束现为 ${\dot{m}}_{m e l t} \geq - {\dot{m}}_{d}$ ，即：允许冻结，但冻结速率不得超过流入液体速率。

此过程的能量平衡为：

图 9. EQUATION_DISPLAY

{\dot{m}}_{m e l t} h_{s} (T_{i c e}) + \frac{\sum_{}^{} m_{d} [h_{L} (T_{d}) + \frac{1}{2} v_{d}^{2}]}{A_{s, b} Δ t} + q = (1 - C_{e m p}) q + {\dot{m}}_{r u n - o f f} h_{L} (T_{F})

(222)

其中：

图 10. EQUATION_DISPLAY

{\dot{m}}_{m e l t} = \frac{C_{e m p} q + \frac{\sum_{}^{} m_{d} [C_{p, s} (T_{d} - T_{F}) + \frac{1}{2} v_{d}^{2}]}{A_{s, b} Δ t}}{C_{p, s} (T_{F} - T_{i c e}) + L}

(223)

对于固体颗粒的吸积，可以进行类似的分析。

吸积率

根据 Makkonen [195]，按如下所示定义非零 ${\dot{m}}_{d}$ 的吸积率十分有用：

图 11. EQUATION_DISPLAY

α = - \frac{{\dot{m}}_{m e l t}}{{\dot{m}}_{d}}

(224)

此物理量反映了吸积过程的特性。当 $α = 1$ 时，没有径流，进行“干”吸积，这往往会形成霜冰。否则存在一些径流，“湿”吸积会逐渐增加，形成雨凇。吸积率有时也称为“冻结分数”。