Controlling a K-Omega Model

Accounting for Strong Streamline Curvature and Frame-Rotation

Curvature correction is a factor that alters the turbulent energy production term according to local rotation and vorticity rates.

The Curvature Correction Parameters node provides the properties with which you can control the curvature correction factor. It is activated as a sub-node of any K-Omega model node when the Curvature Correction Option property is activated.

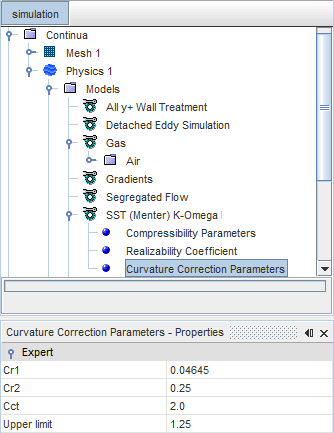
This feature is deactivated by default. It is only necessary for cases that have strong streamline curvature or a rapidly rotating reference frame. Only activate this feature to improve the results when you have a stable solution.

Overcoming an Unexpectedly Large Growth of K

It has been observed [321] that two-equation models predict an unexpectedly large growth of turbulent kinetic energy in stagnation point flows. This issue can have an adverse effect on the rest of the flow solution. To overcome this issue, a lower limit on the turbulence time scale has been proposed that imposes the “realizability” constraint on the eddy-viscosity formula. The Realizability Option property of the parent model object is set to Durbin Scale Limiter.

The effect of this coefficient can be demonstrated by observing the difference between two solutions of flow over an airfoil. In the first solution that is shown below, the realizability option has not been activated. The build-up of turbulence at the stagnation point is clearly observed. In the second solution, the realizability option has been activated.

This time scale realizability constraint is applied by default to the K-Omega turbulence models in Simcenter STAR-CCM+.

Turbulence Damping for Free-Surface Waves

In free-surface flows, two-equation turbulence models occasionally predict an excessive turbulent viscosity and a pronounced velocity gradient within the near-potential flow zone beneath waves, at the interface of the two fluids. This results in a rapid production of turbulent kinetic energy and eddy viscosity. This phenomenon influences various aspects of fluid dynamics, particularly wave dynamics, causing a gradual decrease in wave amplitude over multiple wavelengths, typically required for marine and offshore simulations. Consequently, this can impact the predicted forces acting on structures, resistance experienced by ships, and wave breaking.

To overcome this effect, a limiter on the eddy viscosity turbulence time scale is used that imposes a vorticity coefficient constraint for turbulence damping. To apply turbulence damping, set Realizability Option property of the K-Omega turbulence model to Vorticity Limiter. This method is available only for Volume Of Fluid (VOF) wave simulations, using the VOF Waves model.

The effect of this coefficient can be demonstrated by observing the difference between two solutions of ship waves shown below. In the first solution, where the Vorticity Limiter realizability option is not activated, wave damping occurs. In the second solution, where the Vorticity Limiter realizability option is activated, the wave amplitude (position in Z) is preserved.

Realizability Option: None	Realizability Option: Vorticity Limiter

For more information, see Realizability Option.

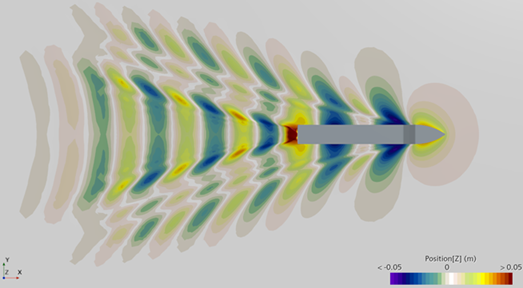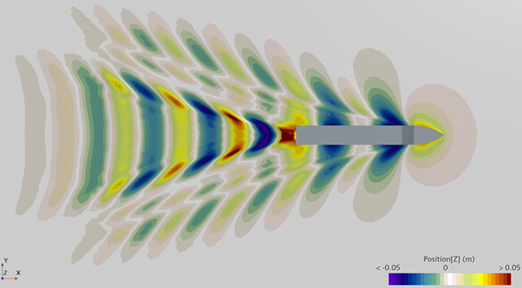Accounting for Low Reynolds Number Effects

The Low Re Damping Modification property of a K-Omega model is needed for low Reynolds number flows, or when it is important to predict turbulent quantities close to surfaces.

The Low Re Damping Parameters sub-node provides the properties with which you can control the damping modification.

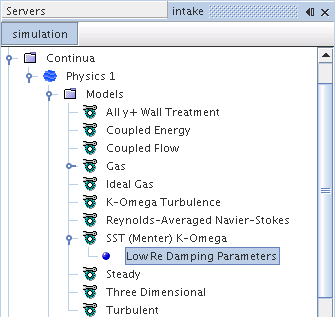
This feature is deactivated by default. It is not needed for low- $y^{\text{+}}$ wall treatment, only for “transitional flows”. Although further development is required to make it reliable as a transition model, it can handle laminar bubble transition to some degree. It is not compatible with the Gamma ReTheta Transition model.

Overcoming the Round/Plane-Jet Anomaly

Almost all two-equation models tend to predict a larger spreading rate for round jet than for plane jets, while the opposite effect is observed in experiments. The Vortex Stretching Modification property of the Standard (Wilcox) K-Omega model allows you to remedy this problem. This model is suitable for most cases where flow separates from a surface.

This feature is deactivated by default.

Accounting for Compressibility Effects

The compressibility correction that is implemented for the K-Omega models allows you to account for dilatation dissipation and enhances the prediction of flows where compressible effects are dominant.

The Compressibility Parameters node provides the properties with which you can control the compressibility correction. It is activated as a sub-node of any K-Omega model node when the Compressibility Correction property is activated.

Improving Predictions for Free-Shear Flows

The free-shear modification improves predictions for flows that are dominated by free-shear layers (like jets and mixing layers) or when free-stream turbulence is high.

The Free-Shear Modification property is available for the Standard (Wilcox) K-Omega model and is deactivated by default. The following modification methods are available:

• Dissipation Limiter
• Cross-diffusion Limiter

Accounting for Anisotropy of Turbulence

You can account for anisotropy of turbulence by extending the Boussinesq approximation to include non-linear functions of the strain and vorticity-rate tensors. Using non-linear constitutive relations improves turbulence prediction for flows with strong secondary recirculation, streamline curvature, or where highly non-equilibrium conditions are prevalent.

The Constitutive Option property is available for the SST (Menter) K-Omega model. Two non-linear relations are available:

• QCR (Quadratic Constitutive Relation)
• Cubic

The Quadratic relation improves the performance of the SST (Menter) K-Omega model by predicting secondary flows better.

The Cubic relation extends the non-linear constitutive relation of the Quadratic relation by including cubic functions of the velocity gradients. These additional terms improve the sensitivity of the SST (Menter) K-Omega Model to streamline curvature.