Controlling a K-Epsilon Model
Accounting for Strong Streamline Curvature and Frame-Rotation
Curvature correction is a factor that alters the turbulent energy production term according to local rotation and vorticity rates.
The Curvature Correction Parameters node provides the properties with which you can control the curvature correction factor. It is activated as a subnode of any realizable K-Epsilon model node when the Curvature Correction Option property is enabled.
This feature is disabled by default. It is only necessary for cases that have strong streamline curvature or a rapidly rotating reference frame. In addition, we recommend you activate it only when you have a stable solution, to improve the results.
For more information, see Curvature Correction Option.
Overcoming an Unexpectedly Large Growth of K
Two-equation models predict an unexpectedly large growth of turbulent kinetic energy in stagnation point flows [321]. This growth can have an adverse effect on the rest of the flow solution. To overcome this effect, a lower limit on the turbulence time scale has been proposed that imposes the “realizability” constraint on the eddy-viscosity formula. To apply it, set the Realizability Option property of the parent model object to Durbin Scale Limiter.
The effect of this coefficient can be demonstrated by observing the difference between two solutions of flow over an airfoil. In the first solution that is shown below, the Realizability option has not been activated. The build-up of turbulence at the stagnation point is clearly observed. In the second solution, the Realizability option has been activated.

For more information, see Realizability Option.
Turbulence Damping for Free-Surface Waves
In free-surface flows, two-equation turbulence models occasionally predict an excessive turbulent viscosity and a pronounced velocity gradient within the near-potential flow zone beneath waves, at the interface of the two fluids. This results in a rapid production of turbulent kinetic energy and eddy viscosity. This phenomenon influences various aspects of fluid dynamics, particularly wave dynamics, causing a gradual decrease in wave amplitude over multiple wavelengths, typically required for marine and offshore simulations. Consequently, this can impact the predicted forces acting on structures, resistance experienced by ships, and wave breaking.
To overcome this effect, a limiter on the eddy viscosity turbulence time scale is used that imposes a vorticity coefficient constraint for turbulence damping. To apply turbulence damping, set Realizability Option property of the K-Epsilon turbulence model to Vorticity Limiter. This method is available only for Volume Of Fluid (VOF) wave simulations, using the VOF Waves model.
| Realizability Option: None | Realizability Option: Vorticity Limiter |
|---|---|
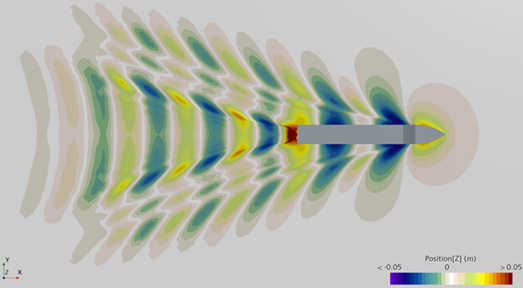 |
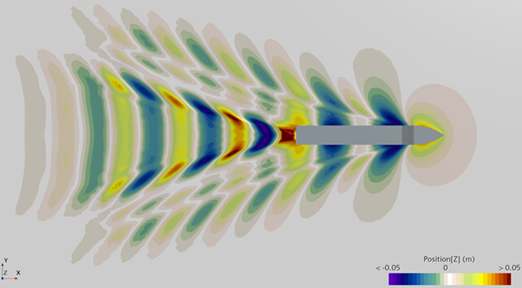 |
Accounting for Anisotropy of Turbulence
You can account for anisotropy of turbulence by extending the Boussinesq approximation to include non-linear functions of the strain and rotation tensors. These non-linear constitutive relations improve turbulence prediction by including effects such as secondary flows, streamline curvature and rotation [311].
Relation coefficients appear as sub-nodes of the Standard K-Epsilon, Standard Two-Layer K-Epsilon, or Standard Low-Reynolds Number model node, depending on the Constitutive Relation property setting of that node. Two non-linear relations are available:
- Quadratic
- Cubic
The Quadratic relation improves the performance of the K-Epsilon model by predicting secondary flows better.
The Cubic relation extends the non-linear constitutive relation of the Quadratic relation by including cubic functions of the velocity gradients. These additional terms improve the sensitivity of the K-Epsilon Model to streamline curvature and rotation.
For more information, see Constitutive Relation.