Operators and Functions

Arithmetic Operators

Logical Operators

Logical operators allow you to write conditional expressions. See Conditional Expressions.

Trigonometric Functions

Trigonometric functions accept a scalar expression (that is, an expression that evaluates to a scalar) as input, returning a scalar. The input scalar expression can be space or time dependent. If the input depends on space, or time, the returned quantity also depends on space, or time.

In the following table, x and y indicate input scalar expressions. The input scalar expression could simply be a constant value (for example, cos(3.14), sin(6.28)), or an expression that references other scalar quantities (for example, sin(2*${omega}*${Time}), where omega is a scalar parameter and Time is the Time field function).

Vector Functions

Vector functions accept a vector expression (that is, an expression that evaluates to a vector) as input, returning either a scalar or vector quantity. The input vector expression can be space or time dependent. If the input depends on space, or time, the returned quantity also depends on space, or time.

In the following table, u and v indicate input vector expressions. The input scalar expression could be a constant vector (for example, u = [0.5, 1, 2], or an expression that references other vector quantities (for example, u = ${coefficient}*$${Velocity}, where coefficient is a scalar parameter and Velocity is a vector field function).

When applying the dot or cross vector functions, supply both vectors with reference to the same Cartesian coordinate system.

When plotting vector fields within a vector displayer, the vector is always considered defined in the laboratory Cartesian coordinate system.

Symmetric Tensor Functions

Tensor functions accept tensor quantities as inputs, returning either a scalar or vector quantity. In the following table, the field function A represents a 3x3 symmetric tensor $\mathbf{A}$ :

$$$A.dot($$$B), 
						

dot($$$A, $$$B)

$$$A.dotVector($$v),

$$v.dotVector($$$A),

dotVector($$$A, $$v),

dotVector($$v, $$$A)

Miscellaneous Functions

In the following table, x and y indicate input scalar expressions.

Conditional Expressions

The ternary “?:” operator defines a condition operation if-then-else similar to the C language. For example:

(a > b) ? a : b

is equivalent to

z = max(a, b)

You can also use parentheses to nest conditional expressions.

Nested conditional expressions allow you to specify different values for a user field function over different time intervals:

($Time <= t_1) ? Value 1 : 
( 
($Time > t_1 && $Time <= t_2) ? Value 2 : Value 3
)
)

For example, consider a case where the value alternates between 125 and 0 in five-second intervals, and remains at 0 after 15 seconds:

($Time <= 5) ? 125 : 
( 
($Time > 5 && $Time <= 10) ? 0 : 
( 
($Time > 10 && $Time <= 15) ? 125 : 0
)
)

The ternary “?:” operator requires all fields to be available on the part (such as the boundary or volume). If one of the fields is not available on the part, then the entire user-defined expression involving the “?:” operator is judged to be invalid and Simcenter STAR-CCM+ fails to fill the field function. In this case, you would see gray in a scene instead of the expected results.

Alternate Value Function

If the value for a scalar or vector expression on a part is not available or computable, you can provide an alternate value for that expression.

Normally Simcenter STAR-CCM+ requires all terms in an expression to exist for the expression to be computable. For example, in the following expression:

$Pressure * $Volume

if Pressure, Volume, or both do not exist for a part, this expression is not computable on that part.

To provide an alternate value, use the alternateValue() operator:

alternateValue($Pressure, 0) * $Volume

In this example, Simcenter STAR-CCM+ substitutes zero for Pressure if Pressure is not available.

The alternate value operator is not restricted to constants; it can also work with another expression. The syntax for this use of the operator is alternateValue(<scalar/vector expression 1>, <scalar/vector expression 2>), for example:

alternateValue($Pressure1, $Pressure2) * $Volume

In this example, if both Pressure1 and Pressure2 are not computable, then the alternateValue expression is not computable.

Interpolation of Direction from Parts

The interpolateDirection function generates a field of direction vectors based on the part curves, surfaces, or a filter that you specify. Having a field of direction vectors can be useful when you model anisotropic behavior in materials.

interpolateDirection(@Part("<partname>"), @Representation("<representation>"), @CoordinateSystem("<coordinatesystem>"), <direction>) 

interpolateDirection(@Filter("<filter>"), @Representation("<representation>"), @CoordinateSystem("<coordinatesystem>"), <direction>)

where:

• <coordinatesystem> is the name of a coordinate system in the Tools > Coordinate Systems node in the object tree. The direction vectors are returned based on this coordinate system. If you do not specify a coordinate system, the function uses the default Laboratory coordinate system.
• <partname> is a surface or a curve. For a surface, the direction field is given using the normals of that part. For a part curve, the direction field is given using the line segment directions. If using a surface or a part curve name of a part, the syntax is <partname.surface/curve name>.
• <representation> is the representation that is used to extract the part. It is set in the Representation node in the object tree.
• <direction> defines the orientation of the vectors based on the direction of the normals of the input surface or the direction of the line segment of the input line. Use FORWARD to follow the direction vectors or BACKWARD to reverse the direction vectors.
• <filter> is a filter defined under the Automation > Filters node in the simulation tree. The filter can be used to define any compatible objects including multiple part curves or surfaces.

interpolateDirection(@Part("<partname1>::<partname2>::<partname3>"), @Representation("<representation>"), @CoordinateSystem("<coordinatesystem>"),FORWARD)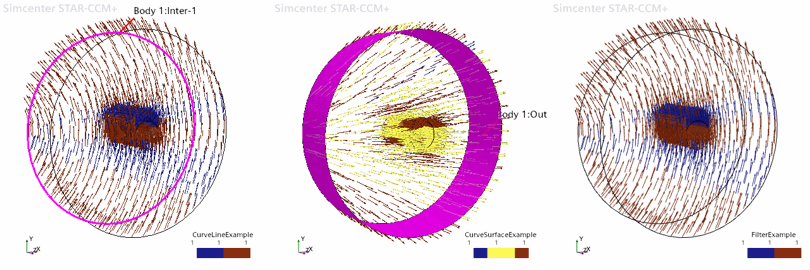 

The following is an example of using this function. The left image is a tangential field function that uses a part curve input. The central image shows a radial field function that uses a surface input for the given geometry. The right image shows a radial field function that uses a filter input for the given geometry.

InsidePart Field Function

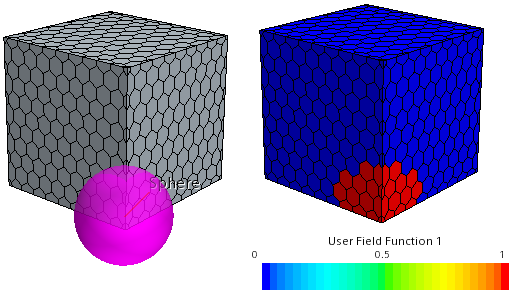
The insidePart function provides a 0-1 field of values that indicate whether points lie outside (0) or inside (1) a spatial location described by geometry parts. This function is useful in defining initial conditions on part of a mesh, for example.

The insidePart function always returns a value of 0 or 1; 0 indicates points are outside the specified part whereas 1 indicates points are within the specified part. The insidePart function accepts two types of argument: @GeometryPart and @Filter.

insidePart(selectorParam, tolerance)

insidePart(@GeometryPart("<geometrypart>"))

where:

If a part belongs to a composite part then you must include vertical bars in the @GeometryPart argument that distinguish between the names of the items. For example, the image below shows a cylinder part that belongs within a composite part:

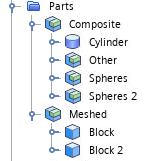
The syntax to identify the cylinder part by name is:

insidePart(@GeometryPart("Composite|Cylinder"))

insidePart(@Filter("<filter>"))

where:

The following image shows an example of this function's use in an expression. The blue color (value 0) on the block indicates the portion of the mesh outside the sphere and the red color (value 1) indicates the portion of the mesh inside the sphere.

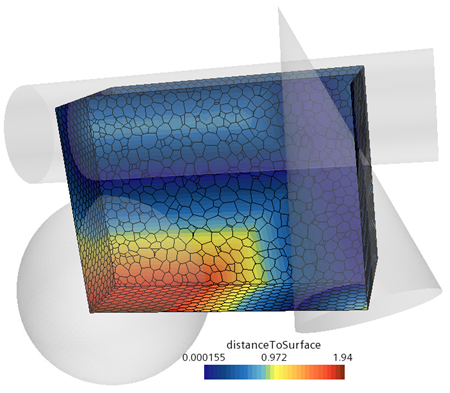
DistanceToPart and DistanceToSurface Field Function

The distanceToPart and distanceToSurface functions provide a field of values that indicate the distance to a given part or part surface.

The distanceToPart function returns the distance to a part or set of parts. The parts provided to the function must be closed and manifold.

distanceToPart(selectorParam, maxSearchDistance)

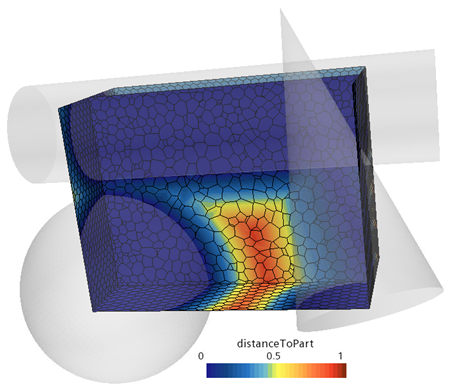
The distanceToSurface function returns the distance to a part surface. This function allows you to include parts that are not closed or manifold.

distanceToSurface(selectorParam, maxSearchDistance)

The distanceToSurface field function always uses the root description of the geometry so it is unaware of any imprint surfaces (which only impact a later description).