多孔阻力属性设置示例

可以采用多种不同的方式指定多孔阻力属性，具体取决于要建模的多孔介质的特性以及通过它的预期流动条件。

为了能够通过使用场函数和表达式（以及常数值）来指定多孔阻力，Simcenter STAR-CCM+ 提供了一个架构，可用于定义用户自己的阻力模型。本节介绍如何完成此操作的一些示例。

正交各向异性粘性阻力

考虑通常用于规定管和管道中的流动条件类型的管束。此多孔介质位于与 x 轴成 45 度的管道截面内，如下所示。

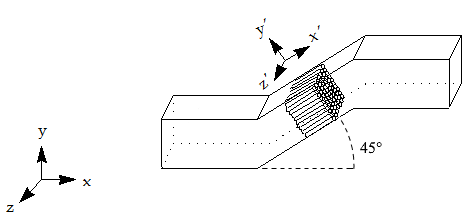
在风洞（工作流体为空气）内进行的测量显示，当速度为 1 m/s 时，管束装置会造成每米 70 Pa 的压降。此外，在相关速度范围内，压降随速度呈线性变化。

由于雷诺数很低，只需指定粘性阻力张量 $P_{v}$ ，因此多孔阻力是流速的线性函数。在正交各向异性坐标中，主系数为 70。要限制垂直于主方向的方向上的流，需要选择比主系数大 2-3 个数量级的阻力系统，例如 10000。选择较大的阻力不会影响流体，但会对收敛特性造成不利影响。因此，采用正交各向异性坐标的粘性阻力张量的选择如下所示：

[\begin{matrix} 70 & 0 & 0 \\ 0 & 10000 & 0 \\ 0 & 0 & 10000 \end{matrix}]

可以在 Simcenter STAR-CCM+ 中使用正交各向异性张量分布法指定此张量：XX、YY 和 ZZ 分量分别为 70、10000 和 10000。方向管理器 > [局部方向] > Principle Axis 1(主轴 1) 为相对于基准坐标系的矢量 (1, 1, 0)，表示与基准坐标系的 x 轴呈 45 度倾斜的矢量。Principle Axis 2(主轴 2) 为 (-1, 1, 0)，同样相对于基准坐标系。

使用 Ergun 方程（适用于填充层的 Forchheimer）的各向同性阻力

描述通过多孔介质的流体的经典方程之一是达西定律，它根据渗透率的度量将流速与压力梯度相关联。应用于蠕流 ( $Re ≪ 1$ ) 的此定律使用 [425] 表示如下：

图 1. EQUATION_DISPLAY

- \nabla p = \frac{μ}{k_{p}} v_{s}

(237)

其中， $μ$ 为流体分子粘度， $k_{p}$ 为渗透率（视为多孔介质的特性属性）， $v_{s}$ 为通过介质的表观速度。

随着流速的增加，速度和压力梯度之间的关系变为非线性。Dupuit 和 Forchheimer（如 [425] 中报告）提议添加二次项，如下所示：

图 2. EQUATION_DISPLAY

- \nabla p = \frac{μ}{k_{p}} v_{s} + b ρ | v_{s} | v_{s}

(238)

Eqn. (238) 通常称为 Forchheimer 方程 [425]。因子 $b$ 必须根据特定流体和相关介质推导得出，且通常通过实验加以确定。

对于特定类别的流体，Forchheimer 方程的一个示例为 Ergun 方程（如 [156] 中所述）。此方程是针对流体（流经填充层）长度 $L$ 方向上的压降 $d p$ 的经验模型：

图 3. EQUATION_DISPLAY

- \frac{d p}{L} = P_{v} + P_{i} = \frac{150 μ {(1 - χ)}^{2} v_{s}}{χ^{3} {D_{p}}^{2}} + \frac{1.75 ρ (1 - χ) v_{s}^{2}}{χ^{3} D_{p}}

(239)

其中：

$P_{v}$ 和 $P_{i}$ 分别为粘性项和内部项。
$ρ$ 为流体密度。
$D_{p}$ 为多孔介质中颗粒的平均直径。
$χ$ 为体积孔隙率。

通过比较 Eqn. (239) 与 Eqn. (238) 表明，渗透率和 $b$ 因子如下：

图 4. EQUATION_DISPLAY

\frac{1}{k_{p}} = \frac{150 {(1 - χ)}^{2}}{χ^{3} {D_{p}}^{2}}

(240)

且

图 5. EQUATION_DISPLAY

b = \frac{1.75 (1 - χ)}{χ^{3} D_{p}}

(241)

要在 Simcenter STAR-CCM+ 中实现此模型，需要为其中每个项创建用户场函数。首先定义体积孔隙率和平均颗粒直径（在此示例中设为常数值）的场函数。然后，这些值将在这两个项的场函数中使用。

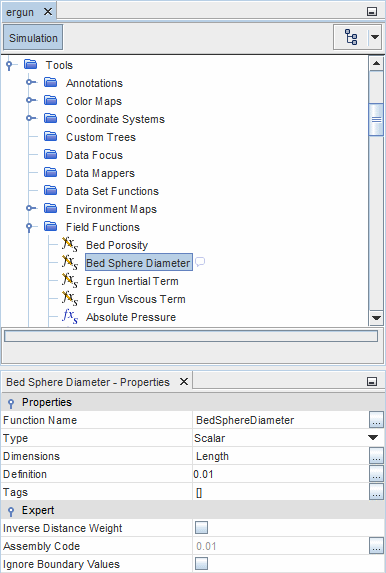
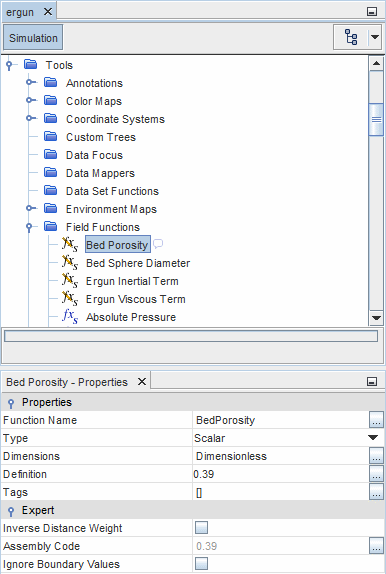
参数场函数

体积孔隙率定义为无维度的标量场函数，其定义设为所需的值（在此示例中为 0.39）。

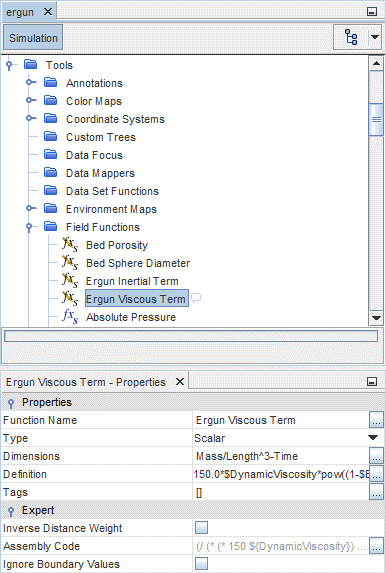
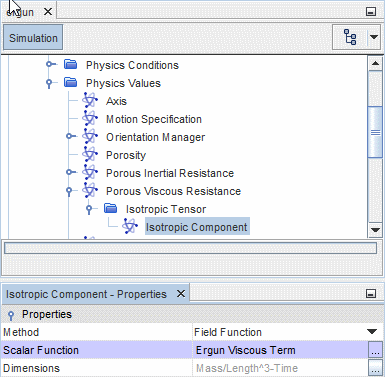
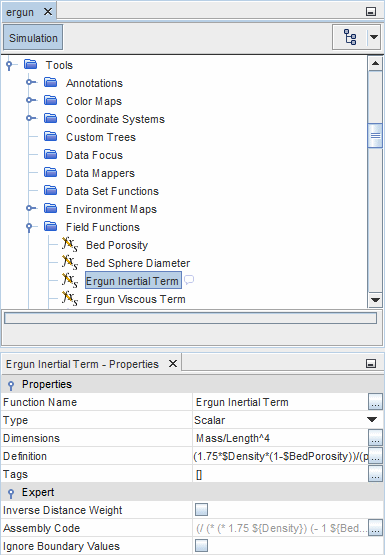
颗粒直径（在此示例中为 0.01 m）以类似方式定义，区别是维度属性设为长度。

粘性项场函数

粘性项的标量场函数的维度是

M a s s \cdot L e n g t h^{- 3} \cdot T i m e^{- 1}

，完整定义为：

150.0*$DynamicViscosity*pow((1-$BedPorosity),2)/(pow($BedPorosity,3)*pow($BedSphereDiameter,2))

此函数使用先前定义的 Bed Porosity(层孔隙率) 和 Bed Sphere Diameter(层球体直径) 函数。

此场函数将作为各向同性张量应用于多孔粘性阻力节点。

选择多孔区域上的物理值 > 多孔粘性阻力节点。
在属性窗口中，使用下拉菜单将方法设为各向同性张量。各向同性张量子节点将显示在多孔粘性阻力节点下方。
选择各向同性张量 > 各向同性分量节点，然后在属性窗口中，将方法设为场函数。
最后，编辑标量函数属性并选择 Ergun Viscous Term(Ergun 粘性项)。

惯性项场函数

惯性项的标量场函数的维度是

M a s s \cdot L e n g t h^{- 4}

，且定义为：

(1.75*$Density*(1-$BedPorosity))/ (pow($BedPorosity,3)*$BedSphereDiameter)

此场函数中包括流体密度。流体密度的任何变化均会影响惯性阻力。像之前一样，通过使用各向同性张量法，此函数适用于多孔惯性阻力：

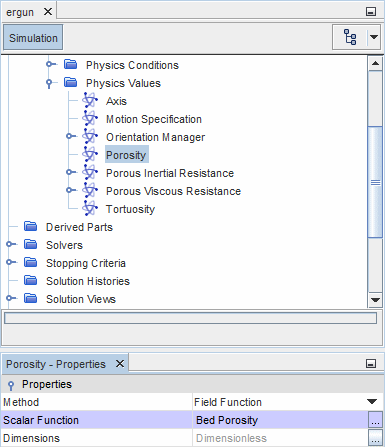
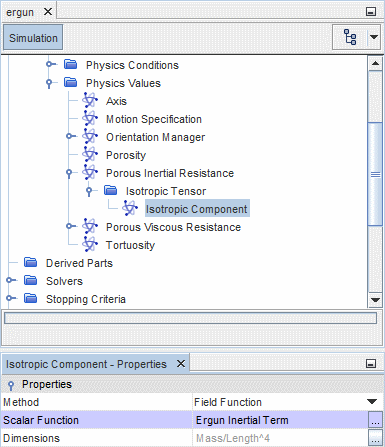
区域孔隙率

在非稳态计算中，可使用 Bed Porosity(层孔隙率) 场函数在区域上设置体积孔隙率

χ

。要设置体积孔隙率：

选择多孔区域的物理值 > 孔隙率节点。
在属性窗口中，使用下拉菜单将方法属性设为场函数，然后将标量函数属性设为 Bed Porosity(床孔隙率)。