Radiation Properties on Boundaries

When solving fluid flows in the presence of thermal radiation, Simcenter STAR-CCM+ requires additional input that characterizes the radiation properties of boundary surfaces.

Kirchhoff's law requires that radiation properties sum up to one on every surface where they are required. Kirchhoff's law is tied to the radiative energy conservation which is in turn tied to the overall energy conservation, so the law must be enforced for virtually all applications. The Kirchhoff Enabled setting of the Gray Thermal Radiation model is on by default.

The radiation properties are defined in the Surface Materials model for each physics continuum. The Surface Materials model contains a user-definable set of surface materials, and is selected automatically when the Radiation model is selected. Each surface material contains the following optical properties:

Emissivity
Reflectivity
Transmissivity
Reflection specularity

Surface materials are then specified in the Regions node for each boundary surface.

Boundaries are classified either as closed, open, or inactive. Closed boundaries require specification of a surface material. In addition, open boundaries require specification of the radiation temperatureT_rad. The radiation does not directly interact with inactive boundaries, so these do not require any further specifications.

If the Radiation Transfer option is set to Internal and External, then each boundary within the region has both Surface Material and External Surface Material nodes, to allow for specification of radiative properties on each side of the boundary.


	Boundary Type			Specify
Boundary Condition	Closed	Open	Inactive	Surface Material	$T_{r a d}$
Inlet: mass flow, stagnation, velocity		X		X	X
Outlet: pressure, flow-split		X		X	X
Wall	X			X
Symmetry plane			X
Cyclic			X
Baffle	X			X

For interfaces, you are required to specify a surface material on each side of the corresponding interface boundary.

While emissivity and reflectivity can be different on each side of the interface, the transmissivity must be the same. In order to satisfy both the second law of thermodynamics and the reciprocity constraint, the transmissivity must be the same for both sides.

With the Participating Media (DOM) model, semi-transmissive external boundaries only interact with the surrounding thermal environment, and not with other objects separated by a space. (The S2S model handles interaction across separating spaces.) If a meshless region, however thin, separates two semi-transparent objects when Participating Media is used for radiation modeling, radiation exchange happens within each object and between each object and the environment, but not between the two objects through the meshless space.

The boundaries at an interface need to be coincident. Since meshing is not perfect, a very small tolerance is allowed between the two sides of the interface. The ray tracing procedure ignores this separation and treats the geometries as coincident. If the two boundaries are not coincident with a too large distance between them, the ray tracing algorithm stops giving meaningful results.

For the Surface-to-Surface (S2S) model, the radiation transfer option can be applied to boundaries. This option can be set to external transfer only, for opaque regions, or external and internal for regions with dual-sided boundaries.

Emissivity

Emissivity is the ratio of the power that a body emits to the power it would emit as a black body at the same temperature (dimensionless). For the Multiband spectrum model, values of this property can be specified for each spectral band.

Reflectivity

Reflectivity is the ratio of reflected radiant energy over incident radiant energy at a given surface (dimensionless).

It can be defined with a material property method or calculated automatically using the Auto-Calculate method. The Auto-Calculate method is the easiest and preferred approach. When this method is selected, the reflectivity is calculated automatically from the specified emissivity and transmissivity using Kirchhoff's law (reflectivity = 1 - emissivity - transmissivity). Anytime afterwards, when you change the emissivity and/or transmissivity, the reflectivity is automatically recalculated. If the reflectivity is entered using a scalar profile, you are responsible for ensuring Kirchhoff's law is satisfied. The only time the Auto-Calculate method must not be used is in the special situation where Kirchhoff's law is explicitly deactivated (see The Gray Thermal Radiation Model).

For the Multiband spectrum model, values of this property can be specified for each spectral band.

Transmissivity

Transmissivity is the ratio of transmitted radiant energy over incident radiant energy at a given surface (dimensionless). For the Multiband spectrum model, values of this property can be specified for each spectral band.

Transmissivity must be same on both sides of an interface or boundary, and therefore must have the same radiation model and spectrum model (gray or multiband) activated for solutions to be valid.

Most radiative models are incompatible with one another, and therefore the transmissivity defined the surface material of each boundary should be set to zero. There are two exceptions: the boundary of a volume region when the Fluid Film and Surface-to-Surface Radiation models are selected. In that case, the boundary on the volume region side of the fluid film interface has transmissivity input instead of the interface. Radiation is not active on the fluid film region side. The other exception is for the case of Volumetric PMC with Surface PMC models, where radiation can be exchanged across interfaces.

Radiation Temperature

Radiation temperature is the temperature of an open boundary that has a total radiant emittance identical to that of a black body radiator (K).

Reflection Specularity

Reflection specularity is the specular fraction of the surface reflectivity:

A value of 0 denotes that all of the reflection is diffuse.
A value of 1 denotes that all of the reflection is specular.
A value in between denotes a combination of diffuse and specular reflection.

Specular reflectivity is determined from the product of reflection specularity and surface reflectivity.

A special case is that of a mirrored surface, which is represented by setting the surface reflectivity and the reflection specularity to 1. This setting means that the surface is completely reflective, and all of the reflection is specular. In this case, the specular reflectivity is also equal to 1. Alternatively, specular reflective surfaces can also be partially transmissive (such as plate glass, particularly low-emissivity glass) or absorptive (such as high-gloss-painted surface). In such cases, the surface reflectivity is less than 1, with surface transmissivity or surface emissivity making up the difference to satisfy Kirchhoff’s law. If part of the reflection is diffuse, the reflection specularity can be set to 1 or less. Specular reflectivity here would thus be less than 1.

Diffuse Radiation Flux

This is diffuse non-Planck radiation unrelated to the temperature of the boundary, although this source can affect the thermal behavior of the far field boundaries and the system being modeled. The source can be either uniform over the spectrum (Gray Thermal Radiation model) or spectrally variant (Multiband Thermal Radiation model). See the theory section for more information. Examples include illumination from LED bulbs or from daylight.

To activate diffuse radiation at a boundary, select Physical Conditions > Radiation Flux Option for the boundary and set the Radiation Flux Option to Diffuse radiation flux. This action adds the node Physics Values > Diffuse Radiation Flux. If you are using the Multiband Thermal Radiation model, this option creates a Composite node with a node for each thermal band under it. If you are using the Gray Thermal Radiation model, there is only one set of properties.Select the method for specifying the flux. The value must be positive.

Directional Radiation Flux

This is non-Planck radiation directed from the boundary but not related to boundary temperature. The source can be either uniform over the spectrum (Gray Thermal Radiation model) or spectrally variant (Multiband Thermal Radiation model). Examples include laser beams and reflected beams of sunlight.

To activate directional radiation at a boundary, select Physical Conditions > Radiation Flux Option for the boundary and set the Radiation Flux Option to Directional radiation flux. This action adds the nodes Directional Flux Orientation and Directional Flux Power Distribution under Physics Values.

If Radiation Transfer Option is set to External or Internal and External, two extra nodes appear under Physics Values, used to describe the directional flux from the external side of the boundary: External Directional Flux Orientation and External Directional Flux Power Distribution.

Directional and External Directional Flux Orientation Properties

Determines the orientation of the directional radiation flux in terms of a direction vector and a divergence angle.

Specify by Part Subgroup: When On, allows you to specify boundaries by subgroups within the region. See Applying Quantities by Subgroup. The default is Off.
Direction: Specifies the direction for the directional flux source with respect to the Coordinate System.
Coordinate System: The coordinate system in which you define Direction.
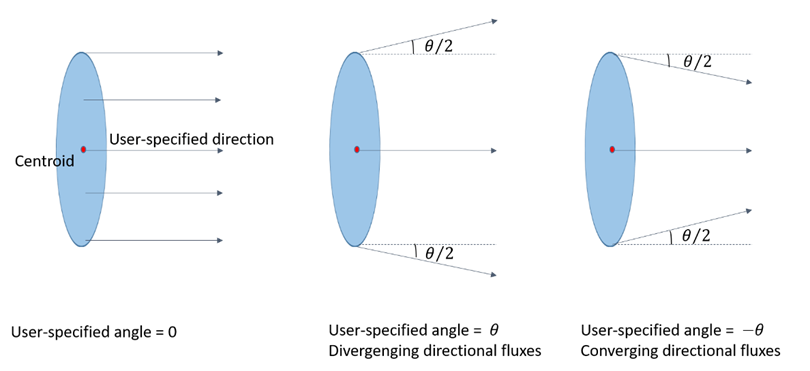
Divergence Angle: Defines the angle of divergence for the directional source as it leaves the boundary. The default is zero, which means that the directional fluxes from the entire boundary are in the specified direction. For a non-zero angle value, the area-based centroid of the boundary is computed and fluxes are then diverged or converged with respect to the centroid. The flux direction at the centroid is set to the specified direction, and the fluxes are diverged or converged (diverged for positive angles, converged for negative angle values) in a linear fashion as a function of distance from the centroid. That is, the divergence or convergence angles vary gradually from zero at the boundary centroid to the half the specified value at the boundary extrema, as shown in the following illustration:

Directional and External Directional Flux Power Distribution Properties

Specifies the directional flux power distribution on the boundary. The value must be positive.

If you are using the Multiband Thermal Radiation model, this option creates a Composite node with a node for each thermal band under it. If you are using the Gray Thermal Radiation model, there is only one set of properties.

Method: The distribution of power on the boundary can be entered as a standard scalar profile, or you can use the Gaussian method.; The Gaussian method allows you to specify a Gaussian power distribution on the boundary, characterized by the Centerline Power value, applied at the boundary centroid, and the rate at which power decays with distance from the centroid, expressed in terms of standard deviation.; The standard deviation is computed internally and set to 1/3.5 of the distance from the centroid to the boundary extrema (the furthest point from the centroid). For this standard deviation, the value at the boundary extrema is close to 1/1000 of the centerline value.; Therefore, for Gaussian method, the recommended boundary is circular, with a radius equal to 3.5 times the standard deviation of the Gaussian energy source.