示例:泡沫导流毛细管压力建模
可以使用用户自定义势能力对毛细管压力进行建模。下面介绍了示例应用“泡沫导流建模”。
对泡沫导流建模是用户自定义势能力的一个应用示例。
泡沫的结构如下所示:

液膜厚度可忽略不计,并且可在 Plateau 边界中捕捉干泡沫中的大多数液体。由于交界面的曲率,液相中存在负毛细管压力 ,用于支持重力下的液体。
此示例使用 Koehler [490] 建议的模型。在干泡沫中,Plateau 边界的曲率半径为:
其中:
- 为 Plateau 边界的特征长度。
- 为液体的体积分数。
毛细管压力为:
其中, 为表面张力。
气相和液相的动量平衡为:
其中:
- 为相的密度
- 为相的速度
- 为液体的粘度
- 为压力
- 为重力加速度。
以下公式中可给定泡沫的渗透率 (Koehler [490]):
其中, 。
此示例将水用作连续相,将空气用作离散相。表面张力视为等于水-空气交界面 ( ),Plateau 边界的长度为 。模拟从 的均匀分布开始。随着液体在重力作用下向下流,将在底部产生纯液体层,而有些液体则被毛细管压力所截留。一段时间后,流动停止并且泡沫将呈现其平衡形状。
假设 表示垂直坐标, 表示液体层的厚度;当 时,这两种相共存。根据 Eqn. (286), ,由此得出 。
因此,力平衡为:
Eqn. (289) 的积分可得出:
根据 求解此方程可得出液体垂直分布的公式:
Eqn. (285) 和 Eqn. (288) 可提供完整的泡沫导流模型。
要在 Simcenter STAR-CCM+ 中实现此模型,应执行以下操作:
- 在液相中,打开 Phase Model Selection(相模型选择) 对话框,然后在可选模型组合框中,选择用户势能力。
-
指定“用户势能”。
在此示例中,此值为 Eqn. (285) 中给定的毛细管压力。
-
指定“用户势能力前因子”。
在此示例中,此值为液体的体积分数 。
-
指定“用户势能体积分数导数”。
在此示例中,此值大约等于:
-
在相间相互作用中,将曳力模型设为使用场函数(线性化系数)法。
提供 Eqn. (288) 作为场函数。
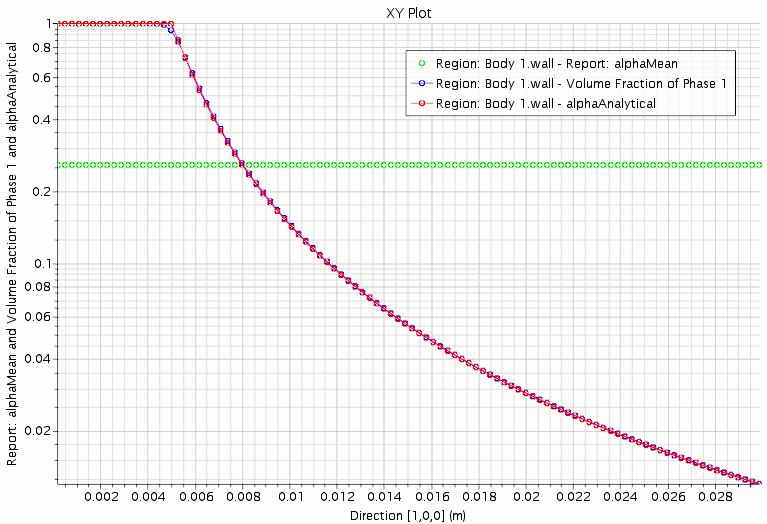
下面显示了模拟结果的示例:静态泡沫中液体垂直分布的绘图。
初始体积分数 绘制为绿色。随着液体沉降,将在底部形成 的区域,但是一些液体仍由气相捕捉。大约五分钟后,流动停止。液相的最终垂直分布(绘制为蓝色)与分析求解(绘制为红色)完全一致。