模型假设和工程方法

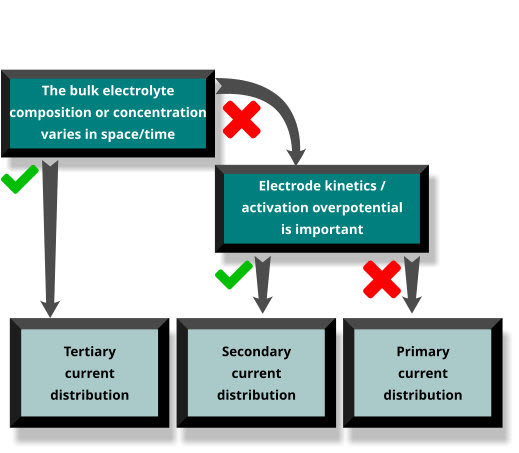
电流分布方法

电化学工程师和科学家根据电流分布概念对模拟进行分类。以下是考虑或忽略的三个主要方面：

1. 因电解质溶液或金属相中的电阻导致的电输运损失
2. 活化过电位
3. 浓度相关反应率和过电位

一次电流分布

一次电流分布设置仅考虑因电阻 (1.) 导致的电传输损失，而忽略 (2.) 和 (3.)。这些模拟不要求解组分浓度，仅需求解电势即可。如果温度也固定，则仅求解电势的一个偏微分方程 (PDE)，从而显著减少计算量。此外，由于电势与组分浓度之间不存在耦合效应，因此计算速度会加快。在 Simcenter STAR-CCM+ 中，仅结合使用电动势模型与电化学反应模型（在这种情况下，将应用最大单位交换电流以最大程度地降低活化过电位）近似此类设置。

忽略活化过电位相当于假设电化学反应率为无限（即，所有重大损失均发生在电解质和/或电荷载体金属输运中）。对于明显快于组分输运的反应，此假设存在矛盾，即：以高进展率达到化学平衡的真实反应可能会消耗反应物，从而降低其速率。但是，一次电流分布设置不考虑任何浓度效应。因此，这些设置不适用于模拟明显快于组分输运的反应。

然而，正如许多（防腐蚀）腐蚀设置中一样，如果反应受金属/溶质输运的限制，则该方法非常有效。尽管这是一种计算性能卓越的建模方法，但建议在 Simcenter STAR-CCM+ 中使用二次电流分布。

二次电流分布

二次电流分布设置建立在一次电流分布的基础之上，但除此之外，还会考虑活化过电位 (2.)。这种处理方法设定的 Simcenter STAR-CCM+ 模型与一次电流分布设置相同，但针对单位交换电流的参数更实际。这种处理在计算开销方面同样表现突出，但提供的结果更为实际，因而建议使用。

二次电流分布设置存在限制，即：不求解组分浓度。因此，二次处理假设电解质均匀混合。但是，在电化学反应率中考虑一定程度的饱和效应，这通常会降低极值，使这些值变得更真实。如果电化学反应不会导致反应物的摩尔浓度明显变化，例如，当反应物过量（例如，海水中的盐）且反应的时间尺度相对对流和扩散流时间尺度来说比较大时，首选这种处理方法。

三次电流分布

三次电流分布建模代表着最详细的建模，其反应率和过电位与浓度相关。在此情景下，(1.)(2.) 和 (3.) 均会考虑。

尽管此情景可提供质量最佳且保真度最高的结果，但所需的计算工作量最大，且对模拟模型参数化的需求也最高。

对于等温三次电流分布设置，将对每个组分求解一个偏微分方程。这些偏微分方程取决于流速，因此将对速度分量求解三个额外方程，而对压力求解一个额外方程。除了电势偏微分方程之外，还求解这些方程。因此，三次电流分布设置需要求解至少 5+n 个偏微分方程，而一次和二次电流分布设置只需求解一个。通常建议额外求解一个温度变化偏微分方程，因为与整体计算量相比，这样做所需的额外计算成本较少。

* 在模拟电化学界面时，需要使用电化学反应模型，以对固体和电解质之间的平衡电势差进行建模。

参数化要求也相当可观。反应必须已知并参数化，才能考虑它们对浓度的依赖性。循环伏安等简单测量不足以对设置进行参数化，必须详细了解过程中涉及的反应机制，这不仅涉及化学计量，而且还涉及每个反应的速率常数和交换电流密度。

当反应物浓度明显影响反应率时，对模型进行详细的参数化可以达到更佳的效果，通常当反应率不是无穷大，但时间尺度等于或小于某个扩散/对流时间尺度时就会出现这种情况，也就是说，在这种情况下，反应物的进给速度或产物的消除速度不足以保持反应率不变。这种情况适用于许多技术应用领域（例如，临界负载情景中的燃料电池）或湿法蚀刻模拟（在此类模拟中，制造速度对于降低生产成本至关重要）。

温度效应

电化学反应率显然与温度相关。然而，对于在固定温度级别发生的工程问题，可以忽略温度求解。

例如，以多年冻土中埋藏的供水管道腐蚀为例。温度由加热元件控制，但研究腐蚀率时，可将此温度视为固定温度。

其他应用需要求解温度。在石油处理管道中，金属温度同时受到空间和时间的影响。如果电化学反应率仍然较低（例如，考虑不必要的腐蚀效应时），可能仍会忽略电化学加热，因为它对总体温度的贡献可以忽略不计。

就一次和二次电流分布设置而言，忽略温度效应对运行时间具有重大影响，在这种情况下只需求解一个偏微分方程。求解三次设置中的温度将在 5+n 个现有偏微分方程中额外添加一个偏微分方程。因此，忽略温度求解只会产生最小限度的节省，为了获得精确的结果，建议不要这样做。