VOF Waves Formulation

Simcenter STAR-CCM+ provides the VOF Waves model to simulate surface gravity waves on the interface between a light fluid and a heavy fluid.

The VOF Waves model supports the following:

First Order Waves
Fifth Order Waves
Cnoidal Waves
Irregular Waves
Superposition Waves
A superposition wave is a linear superposition of two or more first order waves.
Wave Damping
Wave Forcing

First Order VOF Waves

A first order wave is modeled with a first order approximation to the Stokes theory of waves. This approximation generates waves that have a regular periodic sinusoidal profile.

The equation for horizontal velocity is:

图 1. EQUATION_DISPLAY

υ_{h} = a ω \cos (K \cdot x - ω t) e^{K z}

(320)

The equation for vertical velocity is:

图 2. EQUATION_DISPLAY

υ_{v} = a ω \sin (K \cdot x - ω t) e^{K z}

(321)

The equation for surface elevation is:

图 3. EQUATION_DISPLAY

η = a \cos (K \cdot x - ω t)

(322)

where:

$a$ is the wave amplitude
$ω$ is the wave frequency
$K$ is the wave vector
$K$ is the magnitude of the wave vector
$z$ is the vertical distance from the mean water level.

The wave period $T$ is defined as:

图 4. EQUATION_DISPLAY

T = \frac{2 π}{ω}

(323)

The wavelength $λ$ is defined as:

图 5. EQUATION_DISPLAY

λ = \frac{2 π}{K}

(324)

The dispersion relation (between wave period $T$ and wave length $λ$ ) for first order waves in finite water depth $d$ is:

图 6. EQUATION_DISPLAY

T = {[\frac{g}{2 π λ} \tanh (\frac{2 π d}{λ})]}^{- 1 / 2}

(325)

Whereas for infinite water depth, the dispersion relation is:

图 7. EQUATION_DISPLAY

λ = \frac{g T^{2}}{2 π}

(326)

The wave shape is independent of depth.

Fifth Order VOF Waves

A fifth order wave is modeled with a fifth order approximation to the Stokes theory of waves. This wave more closely resembles a real wave than a wave that is generated by the first order method. The wave profile and the wave phase velocity depend on the water depth, wave height, and current.

The fifth order VOF waves are based on work by Fenton [125].

The Ursell number $U_{R}$ is defined as [122]:

图 8. EQUATION_DISPLAY

U_{R} = \frac{H λ^{2}}{d^{3}}

(327)

where $H$ , is the wave height $λ$ is the wavelength and $d$ is the depth of the water.

This wave theory is valid only for Ursell numbers less than 30.

Cnoidal Waves

A cnoidal wave is a nonlinear and exact periodic wave solution of the Korteweg–de Vries equation, which describes the propagation of waves over a flat bed. Korteweg & de Vries [129] obtained periodic solutions which they termed ”cnoidal” because the surface elevation is proportional to the square of the Jacobian elliptic function $c n ()$ . Cnoidal waves are used to describe surface gravity waves that have a long wavelength when compared to the fluid depth. The cnoidal solution displays the long flat troughs and narrow crests that are observed in natural shallow water waves. As the wavelength tends to infinity, the cnoidal solution describes a solitary wave.

The cnoidal solution presents results in terms of expansions in wave height. The parameter that is used is the wave height relative to the trough depth of fluid, $H / h$ , which is denoted by $ϵ$ .

The series is expressed as a power series in $ϵ / m$ rather than $ϵ$ , [124]. As $m$ can be less than 1, it is better to monitor the magnitude of $ϵ / m$ than to have a power series in $ϵ$ with coefficients which are polynomials in $1 / m$ .

The full solution to third order is presented. This solution is more applicable to shorter and reduced-amplitude waves, where the parameter $m$ is less than 0.96.

For small Ursell numbers, the solution scheme for $m$ can fail to converge and this results in an error that indicates that the specific cnoidal wave has an invalid model parameter $m$ . More details regarding the solution approach for $m$ is given in the literature [130].

The symbol $c n$ is used to denote $c n (α X / h | m) = c n (α (x - c t) / h | m)$ .

Surface elevation calculation

图 9. EQUATION_DISPLAY

\frac{η}{h} = 1 + (\frac{ϵ}{m}) m {c n}^{2} + {(\frac{ϵ}{m})}^{2} (- \frac{3}{4} m^{2} {c n}^{2} + \frac{3}{4} m^{2} {c n}^{4}) + {(\frac{ϵ}{m})}^{3} ((- \frac{61}{80} m^{2} + \frac{111}{80} m^{3}) {c n}^{2} + (\frac{61}{80} m^{2} - \frac{53}{20} m^{3}) {c n}^{4} + \frac{101}{80} m^{3} {c n}^{6})

(328)

Horizontal fluid velocity in the frame of the wave calculation

Variation in the $x$ -direction is assumed to be relatively slow and can be expressed in terms of a scaled dimensionless variable $α x / h$ . $α$ is a small quantity which expresses the relative slowness of variation in the $x$ -direction, and $h$ is the trough depth.

The series are expressed in terms of $α^{2}$ (specifically $δ = 4 α^{2} / 3$ ) [126]. The results are accurate even for high waves.

图 10. EQUATION_DISPLAY

\frac{U}{\sqrt{g h}} = - 1 + δ (\frac{1}{2} - m + m {c n}^{2}) + δ^{2} (- \frac{19}{40} + \frac{79}{40} m - \frac{79}{40} m^{2} + {c n}^{2} (- \frac{3}{2} m + 3 m^{2}) - m^{2} {c n}^{4} + {(\frac{Y}{h})}^{2} (- \frac{3}{4} m + \frac{3}{4} m^{2} + {c n}^{2} (\frac{3}{2} m - 3 m^{2}) + \frac{9}{4} m^{2} {c n}^{4})) + δ^{3} (\frac{55}{112} - \frac{3471}{1120} m + \frac{7113}{1120} m^{2} - \frac{2371}{560} m^{3} + {c n}^{2} (\frac{71}{40} m - \frac{339}{40} m^{2} + \frac{339}{40} m^{3}) + {c n}^{4} (\frac{27}{10} m^{2} - \frac{27}{5} m^{3}) + \frac{6}{5} m^{4} {c n}^{6} + {(\frac{Y}{h})}^{2} (\frac{9}{8} m - \frac{27}{8} m^{2} + \frac{9}{4} m^{3} + {c n}^{2} (- \frac{9}{4} m + \frac{27}{2} m^{2} - \frac{27}{2} m^{3}) + {c n}^{4} (- \frac{75}{8} m^{2} + \frac{75}{4} m^{3}) - \frac{15}{2} m^{3} {c n}^{6}) + {(\frac{Y}{h})}^{4} (- \frac{3}{16} m + \frac{9}{16} m^{2} - \frac{3}{8} m^{3} + {c n}^{2} (\frac{3}{8} m - \frac{51}{16} m^{2} + \frac{51}{16} m^{3}) + {c n}^{4} (\frac{45}{16} m^{2} - \frac{45}{8} m^{3}) + \frac{45}{16} m^{3} {c n}^{6}))

(329)

The leading term $- 1$ arises because the wave is considered to be traveling in the positive $x$ -direction. The fluid is flowing under the wave in the negative $x$ -direction, relative to the wave, with velocities of the order of the wave speed.

Vertical fluid velocity calculation

The vertical fluid velocity can be obtained from Eqn. (329) by using the mass conservation equation $\partial U / \partial X + \partial V / \partial Y = 0$ , and $d (c n (θ | m)) / d θ = - s n (θ | m) d n (θ | m)$ . Each term that contains ${(Y / h)}^{i} {c n}^{j} (α X / h | m)$ , for $j > 0$ , is replaced by $α s n () d n () (\frac{j}{i + 1}) \times {(Y / h)}^{i + 1} {c n}^{j - 1} ()$ . Hence, if Eqn. (329) is written as:

图 11. EQUATION_DISPLAY

\frac{U}{\sqrt{g h}} = - 1 + \sum_{i = 1}^{5} δ^{i} \sum_{j = 0}^{i - 1} {(\frac{Y}{h})}^{2 j} \sum_{k = 0}^{i} {c n}^{2 k} () Φ_{i j k}

(330)

where each coefficient $Φ_{i j k}$ is a polynomial of degree $i$ in the parameter $m$ , then the vertical velocity component is:

图 12. EQUATION_DISPLAY

\frac{V}{\sqrt{g h}} = 2 α c n () s n () d n () \sum_{i = 1}^{5} δ^{i} \sum_{j = 0}^{i - 1} {(\frac{Y}{h})}^{2 j + 1} \sum_{k = 1}^{i} {c n}^{2 (k - 1)} () \frac{k}{2 j + 1} Φ_{i j k}

(331)

Irregular VOF Waves

An irregular wave models wind seas (a short-term sea state) with a wave spectrum, that is, the power spectral density function of the vertical sea surface displacement. An irregular wave can use either the Pierson-Moskowitz spectrum or the JONSWAP spectrum [123]. Both spectra describe wind sea conditions that often occur for the most severe sea states.

The Pierson-Moskowitz spectrum available with Simcenter STAR-CCM+, also referred to in literature as the Two-Parameter Pierson-Moskowitz or the Modified Pierson-Moskowitzan spectrum is an adapted representation of the Bretschneider spectrum [120] :

图 13. EQUATION_DISPLAY

S (ω) = A ω^{- 5} exp (- B ω^{- 5})

(332)

The Pierson-Moskowitz spectrum $S_{P M} (ω)$ is then obtained by replacing parameters A and B from Eqn. (332) as $A = \frac{5}{16} (H_{S}^{2} ω_{p}^{4})$ , and $B = \frac{5}{4} (ω_{p}^{4})$ .

where:

$ω_{p} = (2 π) / (T_{p})$ is the angular spectral peak frequency
$H_{S}$ is the significant wave height.

The JONSWAP spectrum $S_{J} (ω)$ is expressed as:

图 14. EQUATION_DISPLAY

S_{J} (ω) = A_{γ} {S_{P M} (ω) γ}^{exp (- 0.5 {(\frac{ω - ω_{p}}{{σ ω}_{p}})}^{2})}

(333)

where:

$S_{P M} (ω)$ is the Pierson-Moskowitz spectrum
$γ$ is the non-dimensional peak shape parameter
$A_{γ} = 1 - 0.287 ln (γ)$ is a normalizing factor
$σ$ is the spectral width parameter:
$σ_{a}$ for $ω \leq ω_{p}$

$σ_{b}$ for $ω > ω_{p}$ .

Wave Damping

Damping of waves is possible by introducing resistance to vertical motion. Simcenter STAR-CCM+ implements the method by Choi and Yoon [121], adding a resistance term to the equation for $w$ -velocity:

图 15. EQUATION_DISPLAY

S_{z}^{d} = - ρ (f_{1} + f_{2} | w |) \frac{e^{κ} - 1}{e^{1} - 1} w

(334)

with:

图 16. EQUATION_DISPLAY

κ = {(\frac{x - x_{sd}}{x_{ed} - x_{sd}})}^{n_{d}}

(335)

where:

$x_{sd}$ is the starting point for wave damping (propagation in the x-direction)
$x_{ed}$ is the end point for wave damping (boundary)
$f_{1}$ , $f_{2}$ and $n_{d}$ are parameters of the damping model
$w$ is the vertical velocity component.

From Eqn. (334), the damping strength indicator $r^{d}$ is given by:

图 17. EQUATION_DISPLAY

r^{d} = \frac{e^{κ} - 1}{e^{1} - 1}

(336)

Wave Forcing

Following the approach of Kim and others ([128]), Simcenter STAR-CCM+ allows coupling of the 3D flow simulation with a theoretical solution that is specified by VOF waves.

Forcing the solution of the discretized Navier-Stokes equations towards another solution (such as a theoretical solution or simplified numerical solution) over a specified distance reduces the computing effort by using a reduced-size solution domain. This forcing also eliminates problems that are associated with reflections of surface waves at boundaries, owing to the damping feature of the gradual forcing.

Wave forcing applies only to Momentum. No Phase sources or Turbulence sources are added. Wave forcing is achieved by adding a source term to the transport (momentum) equations of the form:

图 18. EQUATION_DISPLAY

q_{ϕ} = - γ ρ (ϕ - ϕ^{*})

(337)

where:

$γ$ is the forcing coefficient
$ρ$ is the fluid density
$ϕ$ is the current solution of the transport equation
$ϕ^{*}$ is the value towards which the solution is forced.

When the solution needs to be fixed to a particular value of $ϕ^{*}$ , a large number is used for $γ$ . The remaining parts of the discretized equation then become negligible.

The source term from Eqn. (337) is applied with a variable forcing coefficient over a specified forcing zone. For example, the figure below is a schematic view of two overlapping solution domains. The 3D Navier-Stokes equations are solved in one domain, within the shaded zones. No forcing is applied within the inner zone (3D Navier-Stokes), but within the outer zone (Forcing zone) the forcing source term is activated along the solution domain boundaries. The width of the forcing zone can be different for different boundaries. The optimal width of the forcing zone depends on the problem that you are modeling.

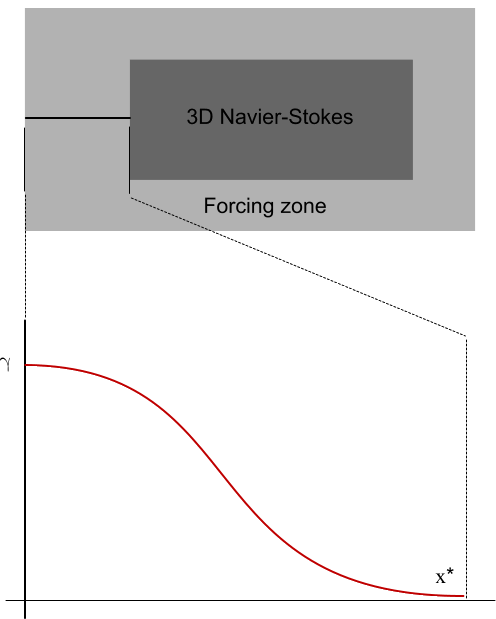
The forcing coefficient varies smoothly from zero at the inner edge of the forcing zone to the maximum value $γ$ at the boundary (the outer edge of the forcing zone).

图 19. EQUATION_DISPLAY

γ = - γ_{0} \cos^{2} (π x^{*} / 2)

(338)

The volume coupling can also be either one-way or two-way, as the forcing zones usually do not coincide.

From Eqn. (338), the forcing strength indicator $r^{f}$ is given by:

图 20. EQUATION_DISPLAY

r^{f} = \cos^{2} (\frac{π x^{*}}{2})

(339)