为一个模式曲线拟合线性模型参数
要校准粘弹性模型的模型参数,从线性参数的聚合物松弛时间和聚合物粘度开始。像以前一样,禁用所有的模型参数,然后绘制和分析一般流体的行为。
使用实验性的 、 曲线的对数绘图来获取线性模型参数的估计初始值:聚合物粘度和松弛时间。在绘图中,您可以找到两条曲线的交点。然后,从 x 和 y 轴上读出 和频率 的值。通过应用下列经验法则,您可以获得曲线拟合算法的合适初始值:
初始松弛时间:
初始聚合物粘度:
对于松弛时间 和粘度 的最小和最大值,使用合理的范围(通常从十分之一的最小值到十倍的最大值)。
可以使用以下关系来计算精确的聚合物松弛时间和粘度的最小和最大值:
- 其中 为频率与 GpGpp 曲线上的最高频率。
- 其中 为频率与 GpGpp 曲线上的最低频率。
- 其中, 和 分别为 和 值的频率。
- 。
要曲线拟合线性模型参数:
-
在扩展的 Pom-Pom 下,右键单击材料校准节点,然后选择拟合工具...。
显示材料参数拟合对话框。该图显示了导入的存储模量和损耗模量曲线。
-
选择 Log 图表选项卡以显示图形的 log-log 版本。
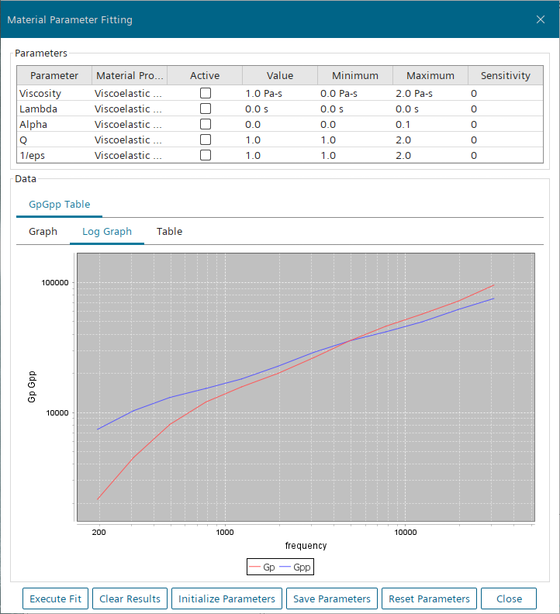
-
检查显示的曲线。请注意,Gp 和 Gpp 曲线相交于频率为 4000/s 处,其中 Gp= Gpp= 32,000 Pa。
Lambda 的初始值是 1/4000 s = 0.00025 s。
粘度的初始值是 2 · 32,000 Pa · 0.00025 s = 16 Pas。
-
输入粘度和 Lambda 的初始值、最小和最大值,如下所示。
将最小和最大值分别指定为初始值的十分之一和十倍,这是一个良好的做法。
参数 值 最小值 最大值 粘度 16 Pa-s 1.6 Pa-s 160 Pa-s Lambda 0.00025 s 0.000025 s 0.0025 s -
通过选择激活并单击执行适配,激活粘度和 Lambda 参数。
调用曲线拟合算法。请注意,结果 1 和结果 2 曲线与 Gp 和 Gpp 曲线不一致,根据单模式粘弹性模型的优化引擎,它们是频谱中最好的候选者。
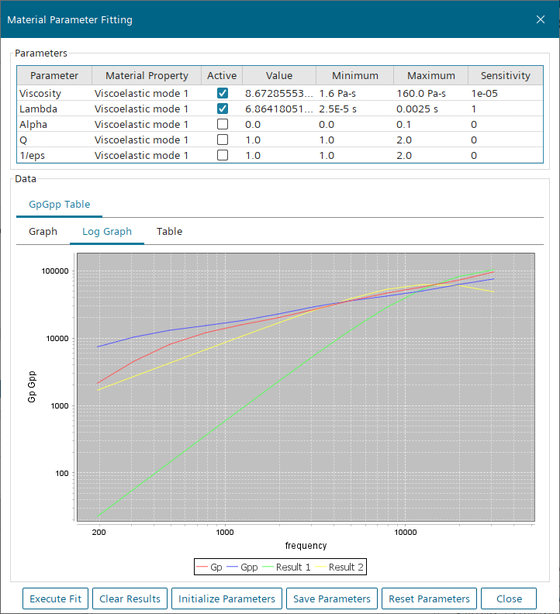
- 单击清除结果和重置参数以恢复曲线拟合的初始状态。
- 禁用粘度和 Lambda 参数
- 单击关闭以关闭对话框。
- 保存模拟。
以下各节另外增加了两个模式来扩展搜索,以便更好地适配。