分析模拟结果
您需要将模拟颗粒体积分数分布与实验数据进行比较,并确认 Morris 和 Boulay 模型适用于对剪切感应颗粒迁移进行建模。
要分析模拟结果:
检查体积分数场景和对应的绘图,以查看 Couette 设备内的模拟颗粒体积分数分布。
-
打开 Volume Fraction of Particles(颗粒的体积分数) 场景并检查颗粒体积分数分布。
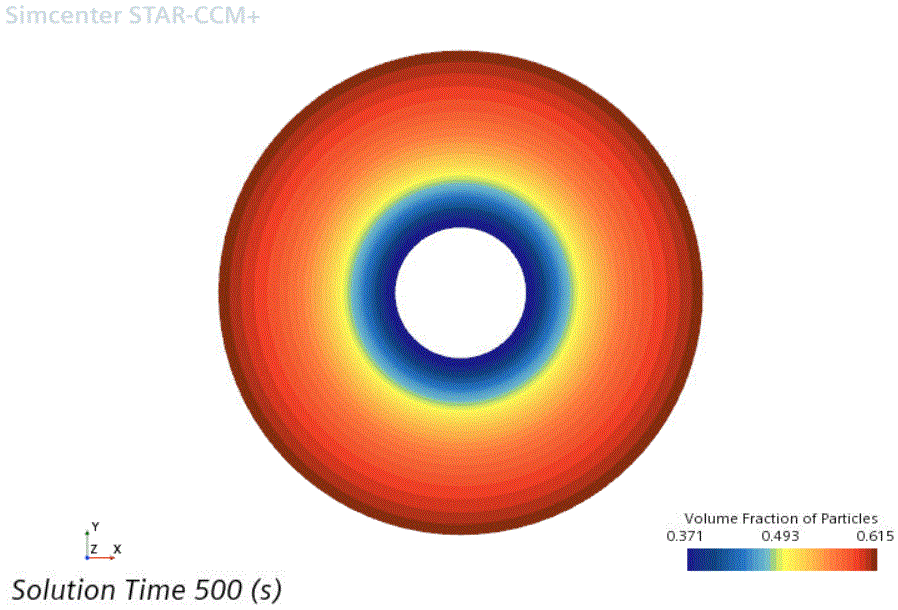
固体颗粒已在剪切流中迁移,朝远离旋转内壁的方向移动。颗粒体积分数的范围为:最小 0.37(靠近内壁),最大 0.615(在外壁处)。
-
打开 Volume Fraction Plot(体积分数绘图) 并将颗粒体积分数分布与实验值进行比较。
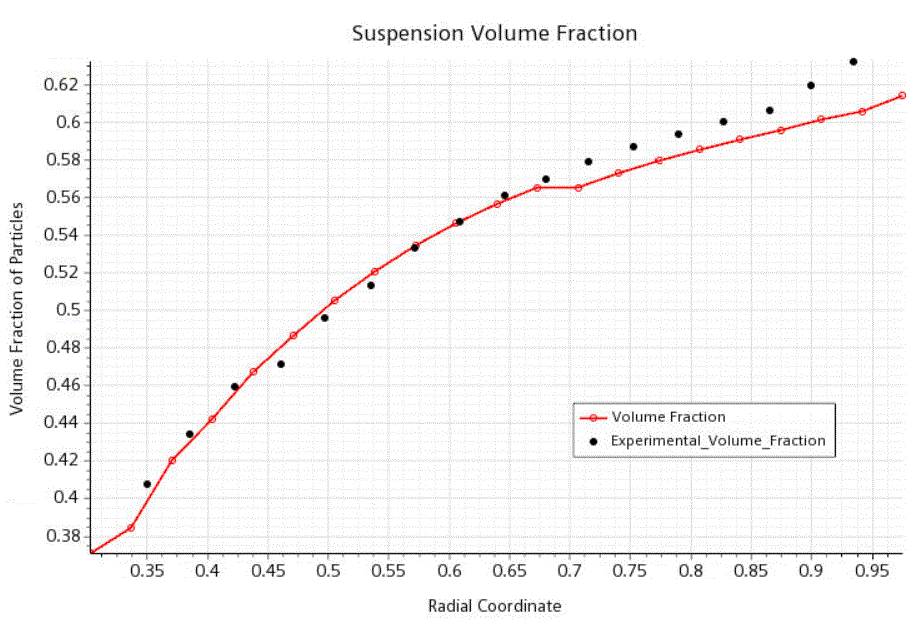
在内部区域,体积分数结果与实验值非常匹配。在外部区域,模拟结果较低,因为在本教程中使用的是粗糙网格。使用更精细的网格会更详细地捕捉颗粒的迁移。
颗粒相压力梯度会驱动颗粒迁移。检查 Phase Particle Pressure(相颗粒压力) 场景,并确认压力梯度最小,这表示颗粒迁移几乎已完成。
-
打开 Phase Particle Pressure(相颗粒压力) 场景,并检查 Couette 设备中的压力梯度。
在模拟前几秒形成的强压力梯度会驱动最初浪涌般的颗粒迁移。下面的示例说明了一秒的物理时间后的压力分布:
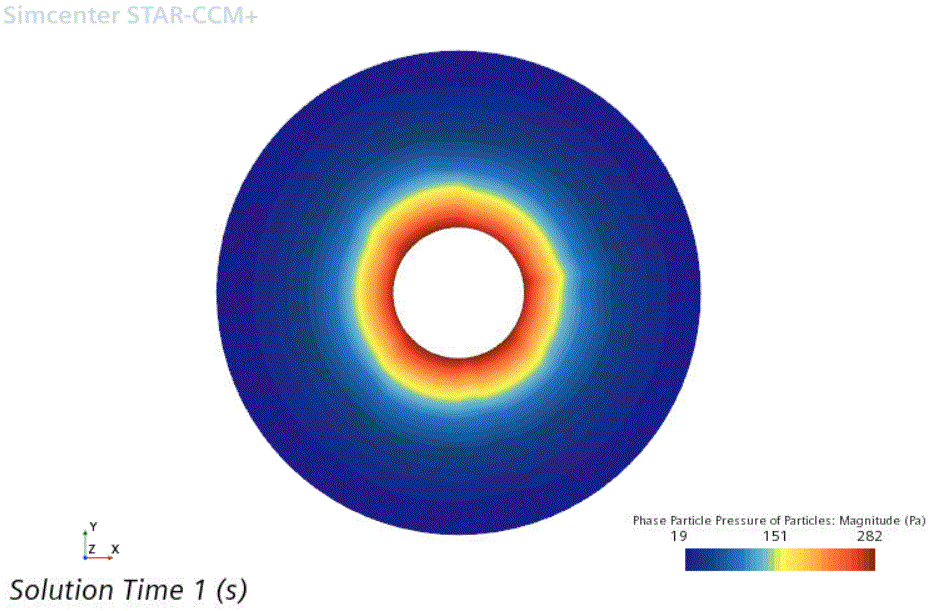
压力分布呈较小的径向梯度逐渐变为低压。在模拟的最后,500 秒的物理时间后,相颗粒压力分布如下所示:
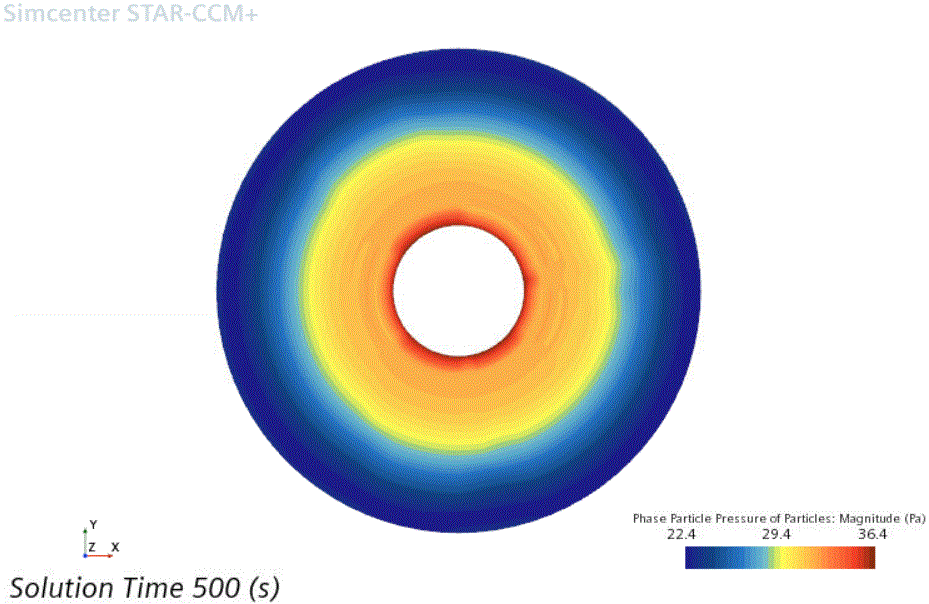
颗粒相压力的范围为约 34(在内壁处)到 22(在外壁处)之间。这种平缓的梯度表明颗粒迁移已放缓,体积分数分布正在趋于稳定。
-
打开 Velocity of Oil(油速度) 场景并检查油速度分布。
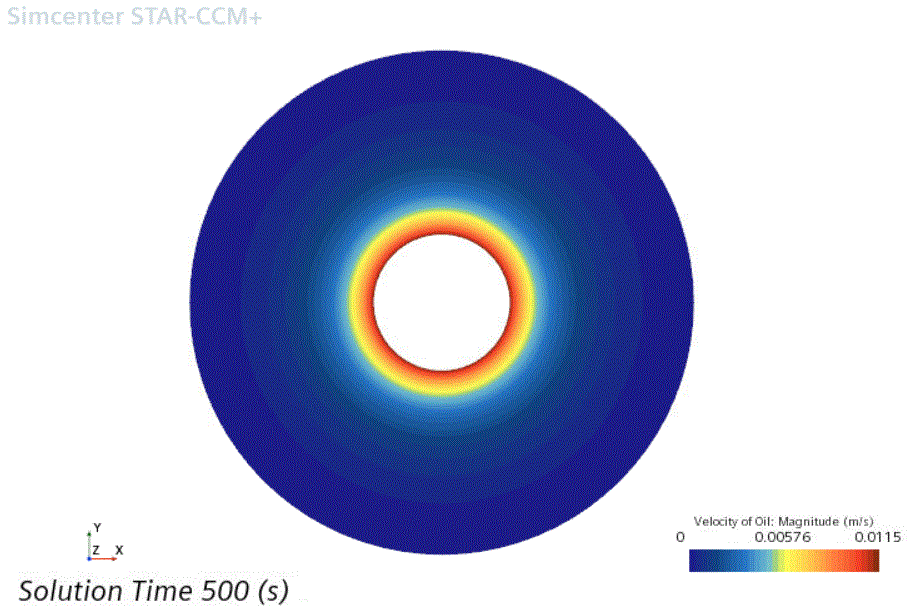
约 300 秒后,油速度分布逐渐进入稳态。在此稳态下,油速度随流体区域内的径向距离而降低;此径向变化会形成导致固体颗粒迁移的流体剪切。
相对粘度取决于颗粒的体积分数,并以颗粒浓度函数的形式呈指数增加。随着颗粒体积分数接近最大填充,粘度将向无穷方向增加。
-
打开相对粘度绘图,并检查粘度随颗粒体积分数的变化情况。
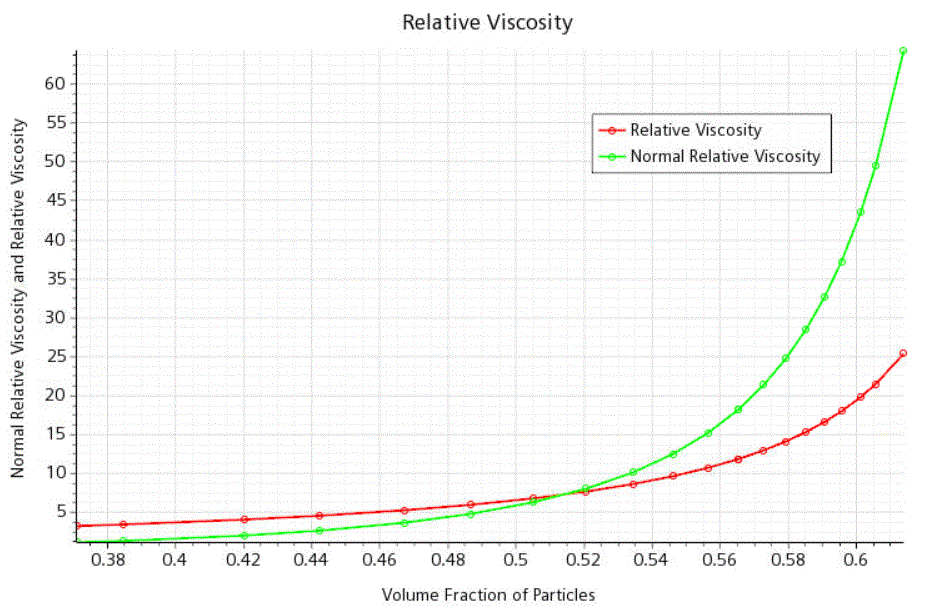
到 500 秒时,在最大体积分数(约 0.615)处,法向相对粘度高达 65。