欧拉：悬浮液流变

本教程演示如何设置对非牛顿浓悬浮液的流进行建模的 Simcenter STAR-CCM+ 模拟。

在本教程中，您将通过 Couette 设备模拟牛顿液体中中性悬浮单分散颗粒悬浮液的低雷诺数旋转剪切流。模拟将预测速度场、颗粒体积分数和颗粒相压力。几何尺寸、旋转速度和材料属性对应于 Philips 等人 [978] 开展的实验调查。模拟结果将与论文中的实验值进行比较。

Phillips 实验测量了因旋转流中的颗粒迁移而导致颗粒体积分数发生的空间变化。悬浮液中的颗粒往往从高剪切速率区域迁移到低剪切速率区域：在 Couette 设备中，颗粒朝远离旋转壁面的方向移动。

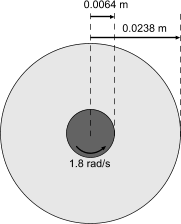
此模拟中使用的几何是 Couette 设备的圆形 2D 横截面。半径为 0.64 cm 的 Couette 设备内壁以 1.8 rad/s 的角速度旋转，它对应的旋转速率大约为 17 rpm。外壁半径为 2.38 cm 并且保持固定。

计算域填充有密度为 1182 kg-m⁻³ 的聚甲基丙烯酸甲酯 (PMMA) 球形颗粒，这些颗粒悬浮在与颗粒具有相同密度并且动力粘度为 4.95 Pa-s 的牛顿四溴乙烷/油混合物中。平均颗粒直径为 0.001 米，颗粒的初始体积分数为 0.55。

几何通过具有 1600 个网格单元的六面体网格进行求解。悬浮液的流通过欧拉多相流方法进行建模。悬浮液的流变描述由 Morris 和 Boulay 模型提供。此模型不仅考虑了纯剪切粘度，还考虑了法向应力效应，法向应力效应会导致流中发生剪切感应颗粒迁移。

在悬浮液流变中，无量纲相对（有效）粘度用于描述混合物粘度。随着越来越多的颗粒相互作用，混合物粘度将随颗粒体积分数以及流体中颗粒之间的流体动力而提高。随着混合物接近颗粒的最大填充，会在颗粒之间形成接触网络并且混合物出现堵塞 [973]，因此，相对粘度趋于无穷大。

在 Morris 和 Boulay 模型中，相对粘度定义为：

其中， $K_s$ 为剪切接触效应， ${\varphi }_m$ 为最大填充分数。

压缩的剪切感应法向应力对颗粒体积分数 $\varphi$ 的依赖性根据法向相对粘度 ${\eta }_n\left(\varphi \right)$ 捕捉，法向相对粘度定义为：

其中， $K_n$ 为法向接触效应。

在此模拟中，法向相对粘度等同于导致颗粒朝剪切速率低的区域迁移的各向同性颗粒压力。

此模拟使用悬浮液的最大填充体积分数 ${\varphi }_m$ ，即 0.68。为了反映颗粒的多分散性，此值高于随机严密填充的理论单分散值（大约为 0.645）。