从二十多年前的公开发行开始,OpenFOAM从根本上颠覆了计算流体力学的世界,其在全世界的学术界和研究中心广泛地传播。 它的成功很大程度上与项目的开源性质和软件的革命性设计有关。 最重要的是,OpenFOAM降低了CFD软件的成本。 由于这个原因,学术界以其丰富的学生劳动,引导了早期OpenFOAM的大部分采用。 开放源码的灵活性允许研究人员以无与伦比的自由进行创新。该行业还对OpenFOAM的定制能力和针对内部问题专门设计的求解器感兴趣。 如今OpenFOAM作为CFD的一个标准为该领域的每个人所熟悉。然而OpenFOAM的所有优势都有一个弱点:缺乏文档及相对陡峭的学习曲线。
从理论上讲,在开源的情况下代码就是文档。一个有经验的用户可以深入到C++的各个层面并理解代码的基本功能。然而对于新用户来说,这种期望是开始使用该软件的巨大障碍。 C++语言和模板化OpenFOAM代码的复杂性加剧了这一困难。即便是像Doxygen这样的工具(它试图对OpenFOAM类结构进行编目)也不能充分减少这些障碍。在用户论坛上,一个沮丧的人哀叹说,对一个C++初学者来说,挖掘Doxygen的输出就像倒着阅读中文。OpenFOAM社区非常需要一种全面的且易于访问的文档形式,为世界各地的OpenFOAM新手提供一个入口。因为OpenFOAM是免费的,学习曲线是OpenFOAM用户进入的根本障碍。
人们可以以合适的价格从OpenFOAM专家那里购买培训,但一流的参考书依然是无可替代的。 多年来,没有任何参考文档为新的OpenFOAM用户提供深度和广度的支持。 这一切在2014年发生了变化,当时Tomislav Marić, Jens Höpken, 及Kyle Mooney出版了《OpenFOAM Technology Primer》。 这本书对那些想要从一个单一的来源可以理解OpenFOAM的人来说是一笔意外之财。 该书的目标受众是那些对CFD有基本背景,但希望更深入地研究OpenFOAM的工作原理和使用方法的人。 尽管我有近十年的OpenFOAM经验,但那本书成了我研究实验室的圣经,就在我的桌子上触手可及。 但在取得巨大成功的几年后,这本书完全消失了。 社区渴望这个可爱的参考资料的回归--直到2021年。
我们现在很幸运,作者们投入了更多的时间来更新和重新发布它。 编写OpenFOAM文档的一个根本挑战是,它是一个不断发展的软件,不断地改变和改进。保持这样一个文档是一个永远做不完的任务,需要一个无休止的承诺。出于这些原因,我很激动地看到作者选择在知识共享许可证下发布文档。就像开源原始OpenFOAM代码的决定一样,这本有价值的书将引领OpenFOAM使用和文档编制的新时代。
Professor David P. Schmidt
Dept. of Mechanical and Industrial Engineering
University of Massachusetts Amherst
Tomislav Marić
Tomislav在克罗地亚萨格勒布大学学习机械工程,并于2017年在德国达姆施塔特工业大学数学系Dieter Bothe教授领导的数学建模与分析研究所(MMA)获得博士学位。在德国达姆施塔特工业大学数学系Dieter Bothe教授的领导下,于2017年获得博士学位。Tomislav目前在达姆施塔特工业大学作为雅典青年研究员工作(2020年10月)。Tomislav自2008年以来一直在开发非结构化的拉格朗日/欧拉界面近似(LEIA)方法,用于OpenFOAM开源软件中的两相流模拟。他与Jens共同创立了sourceflux,自2016年以来,作为达姆施塔特工业大学合作研究中心(CRC)1194的成员,Tomislav在科学软件开发和研究数据管理方面支持CRC-1194的研究人员。
Jens Höpken
Jens在杜伊斯堡-埃森大学学习海军建筑学,毕业于德国杜伊斯堡-埃森大学的船舶技术、海洋工程和运输系统研究所(ISMT)。Jens从2007年开始与OpenFOAM合作,他是一位OpenFOAM专家,在为海军水动力学开发OpenFOAM方面有超过十年的经验。Jens与Tomislav共同创立了sourceflux。
Kyle G. Mooney
Kyle于2016年在马萨诸塞大学阿默斯特分校获得机械工程博士学位。他的研究涉及粘弹性流体和喷雾液滴动力学的数值模拟。研究生毕业后,他加入了ICON技术流程与咨询公司,帮助福特汽车公司、菲亚特克莱斯勒汽车公司和通用汽车公司创新汽车空气动力学模拟流程。在搬到旧金山后,他转向领导流体机械研发工作,同时在几个初创公司进行硬件和软件产品开发。他目前是Geminus.AI的高级应用工程师,为工业应用创建高保真度流动系统仿真模型。在他的空闲时间,你可能会发现他在打拳击、玩滑板、在高山上徒步旅行,或者表演音乐。
计算流体动力学(CFD)开源软件OpenFOAM被广泛应用于工业界和学术界。相较于使用专有CFD软件,使用OpenFOAM的优势在于开源通用公共许可证(GPL),其允许用户自由使用和修改现代高端CFD代码。开源许可消除了产品优化周期中的许可成本,实现了参数变化的直接自动化,并加速了新的数值方法和模型的开发。加快了新方法的开发和实现,因为它们是从OpenFOAM中的现有功能开始的,而不是从头开始的。
除了上面提到的所有优点之外,使用OpenFOAM还有一个缺点。OpenFOAM使用了C++编程语言和现代软件设计模式,因此学习如何以模块化和可持续的方式在OpenFOAM中编写新方法需要付出大量的努力。使用OpenFOAM需要结合不同背景的知识,包括应用数学、物理、软件开发、C++编程语言和高性能计算(并行编程和性能测量)等。
这本书致力于在一个地方描述OpenFOAM的不同方面,帮助初学OpenFOAM的用户发展成为中级OpenFOAM程序员。为了实现这一目标,强烈建议读者通读所涵盖的例子。本书没有介绍OpenFOAM的一些核心部分所必须的C++编程语言的更高级部分。但是这些知识可以在有关C++编程语言和软件设计模式方面的书籍中找到。
本书涵盖了使用OpenFOAM的两个主要方面:使用应用程序以及开发和扩展OpenFOAM应用程序和库。本书第一部分使用几个OpenFOAM实用程序和应用程序描述OpenFOAM工作流程,第二部分介绍了OpenFOAM新求解器和库的开发。
1 目标读者
本书面向对开源计算流体动力学(CFD)感兴趣的任何人。
但是不可能在一本书中提供有效开发OpenFOAM所需的C++编程语言、软件设计、计算流体动力学(CFD)和高性能计算(HPC)的所有背景信息,本书将重点放在OpenFOAM解算器和库的使用、设计和开发上,并引导读者了解那些没有详细介绍的主题所涉及的其他深入信息来源。
因此,假设C++编程语言中的一些面向对象编程知识,涉及类(封装、继承和组合)、虚函数(动态多态性)和运算符重载,这些主题的背景信息在书的第二部分提供。然而,读者也应该使用每章末尾所引用的文献独立地了解这些主题。本书所提供的示例故意避开了验证和确认,因为这会让读者偏离学习OpenFOAM的轨道。然而如果没有计算流体动力学的知识,以及非结构有限体积法(FVM)的知识,就不可能学习和理解OpenFOAM,这本书中简要介绍了该方法,在其他地方也有更详细的介绍。
2 本书涵盖的内容
- 第1章 概述了CFD模拟的工作流程,以及OpenFOAM中的非结构有限体积法(FVM)。
- 第2章介绍了区域离散化(网格生成和转换)及区域分解。
- 第3章描述了仿真实例的结构和设置:设置初始条件与边界条件,配置模拟控制参数及数值参数。
- 第4章概述了前后处理实用程序和数据可视化。
- 第5章对OpenFOAM库进行了深入的概述。
- 第6章描述了如何以高效且可持续的方式编程OpenFOAM:开发和使用库、使用git版本控制系统、调试和分析
- 第7章简要概述了湍流建模:将湍流引入模拟案例并配置湍流模型。
- 第8章介绍了OpenFOAM预处理和后处理应用程序的编程。
- 第9章介绍了OpenFOAM中解算器设计的背景,并展示了如何使用新功能扩展现有求解器。
- 第10章介绍了OpenFOAM中边界条件的数值背景和软件设计。提供了一个自定义边界条件的实现示例,该示例使用了第6章中描述的原则。
- 第11章以温度相关粘度模型为例,介绍了OpenFOAM中输运模型的数值背景、设计和实现。
- 第12章介绍了OpenFOAM中的函数对象的设计与实现,并与C++函数对象进行了比较。
- 第13章介绍OpenFOAM中的动态网格处理。介绍OpenFOAM中动态网格引擎的设计和使用,以及使用动态网格处理扩展解算器。
- 第14章对本书进行了总结。
3 如何阅读此书
对于刚开始使用OpenFOAM的用户,建议从头到尾阅读这本书,并对示例进行独立的研究。有经验的OpenFOAM用户可以从第二部分中选择一章,其中有关于如何对OpenFOAM的某个特定部分进行编程的相关信息。
4 OpenFOAM版本
OpenFOAM有不同的版本可供选择,例如OpenFOAM Foundation、Foam Extended和OpenFOAM。本书没有介绍这些forks之间的区别和相似之处。书中的内容和实例库与OpenFOAM-v2012相匹配,并且该书将只遵循此OpenFOAM版本。
有关如何安装此版本OpenFOAM的信息,请访问其官方网站。可以选择将OpenFOAM作为Linux包安装,编译源代码的快照,或者编译克隆的git存储库。由于本书的目标是解决OpenFOAM编程问题,因此建议编译源代码快照或OpenFOAM git存储库的克隆。
5 命名和排版约定
命令行使用带有前缀?> 的输入。下面是一个示例:
?> ls $FOAM_TUTORIALS
Allclean basic electromagnetics lagrangian
Allrun combustion financial mesh
Alltest compressible heatTransfer multiphase
DNS discreteMethods incompressible stressAnalysis
C++代码排版形式如下所示:
template<class GeoMesh>
tmp<DimensionedField<scalar, GeoMesh> > stabilise
(
const DimensionedField<scalar, GeoMesh> &,
const dimensioned<scalar> &
);
OpenFOAM模拟的配置依赖于所谓的字典文件。字典文件是一种文本文件,以OpenFOAM特有的格式存储键值对的列表:
ddtSchemes
{
default Euler;
}
在方程式中,标量(如通量)的排版没有强调;矢量的排版使用粗体(例如,速度);张量使用粗体和下划线(如单位矩阵)。
6 随书示例
书中包含的示例可以在GitLab上找到: https://gitlab.com/ofbook-/ofprimer。
最新版本合并到主分支中,所有版本都与OpenFOAM git标签版本相匹配,如OpenFOAM-v2012。
7 贡献
错误报告和主题建议使用GitLab服务台处理,并且可以投票表决。支持率最高的话题将有更大的机会在下一版中得到解决。
在提交错误报告或功能请求之前,请搜索existing issues以确保该问题尚未被报告。
本章概述了在OpenFOAM中求解计算流体力学(CFD)问题的工作流程。
此外本章还包含了OpenFOAM所使用的非结构化网格上的有限体积法(FVM)的背景信息,以及对OpenFOAM平台顶层结构的描述。
CFD 分析的目标是更深入地理解所考虑的问题。由于模拟结果通常伴随着实验数据,因此需要考虑结果的有效性和模拟的整体目标。此外,模拟的物理过程需要得到适当的数学建模。为此,CFD 工程师需要在 OpenFOAM 框架中选择合适的求解器。在 CFD 分析过程中,假设可能会使分析变得更加复杂或简化。通常会对模拟域的几何形状进行分析和简化,考虑到可用的计算资源、所需的模拟保真度和期望的运行
任何 CFD 分析的目的都是为了更深入地了解所考虑的问题。由于仿真结果往往伴随着实验数据,因此需要考虑结果的有效性和仿真的总体目标。此外需要对模拟的物理过程进行适当的数学建模,这又要求 CFD 工程师在 OpenFOAM 框架内能够正确地选择合适的求解器。在 CFD 分析过程中,任何假设都可能会使分析变得复杂或简化。考虑到可用的计算资源、所需的仿真保真度以及仿真所需的周转时间,通常会对仿真区域的几何形状进行分析和简化。
下面概述了在进行 CFD 分析项目之前可能提出的实用问题。
1、一般考虑
- CFD 分析得出的结论应该是什么?
- 如何定义计算结果的精度程度?
- 用什么方法来验证计算结果?
- 这个项目有多少时间可用?
2、热物理问题
- 流动是层流、湍流还是转捩流动?
- 流动是可压缩的还是不可压缩的?
- 流动是否包含多种流体相或化学组分?
- 传热在问题中是否起着重要作用?
- 材料属性是否为自变量的函数?例如剪切稀化流体。
- 边界条件和初始条件方面是否有足够的信息?它们是否有适当的模型,是否可以准确地进行近似?
3、几何与网格
- 能否建立流体域的精确离散形式?
- 在模拟过程中,计算域是否会变形或移动?
- 是否可以在不影响求解精度的情况下降低计算区域的复杂性?
4、计算资源
- 有多少可用的模拟计算时间?
- 可用的分布式计算资源有哪些?
- 一次计算就足够,还是需要多次计算?
这些问题有助于对任何流动问题进行精确的 CFD 分析。使用 OpenFOAM 或任何其他 CFD 模拟软件都需要对物理学、数值方法以及可用的计算资源有适当的理解。CFD 的跨学科性质极大地增加了它的复杂性。
CFD 分析通常可细分为 5 个主要步骤。其中一些步骤有时需要进行多次以获取所需的高质量结果。
1.2.1 问题定义
从工程的角度出发,数值模型应尽可能简单,并能准确地描述实际工程系统。忽略模拟问题的无关方面可以提高 CFD 分析的效率,因为它简化了物理过程,从而简化了描述它的数学模型。例如,尽管空气是可压缩的,但在某些流动状态下,模拟机翼上的流动时可以将空气视为不可压缩的流体。
1.2.2 数学建模
一旦物理过程的相关方面被独立出来,问题就需要以数学模型的形式进行描述,这在 CFD 中通常是一组偏微分方程 (PDE)。CFD 工程师必须了解用来描述不同物理现象的模型。在 OpenFOAM 框架中,用户可以在几十种求解器之间进行选择。每个求解器实现一个特定的数学模型,选择正确的数学模型对于获得模拟问题的有效解通常是至关重要的。例如在翼型绕流的问题中,采用不可压缩假设会忽略对能量方程的求解。作为另一个例子,势流只受拉普拉斯方程控制(详情可见 Ferziger 及 Peric(2002)的教材)。若需要考虑更加复杂的物理输运现象,则数学模型的复杂性也会随之增加,这通常导致更复杂的数学模型。例如用于模拟湍流使用雷诺平均 NS 方程(RANSE)。
数学模型描述了流动的细节,这意味着数值模拟最多只能近似模型的解,无法产生比数学模型本身所能描述的更多的关于流动的信息。有关 OpenFOAM 中湍流建模的更多信息可以在第 7 章中找到。关于特定数学模型的更多细节可以在流体力学教科书中找到。
1.2.3 前处理及网格生成
数学模型将物理场定义为模型方程的因变量。在 CFD 中,方程通常描述的是一个边值和初值问题。因此,在开始模拟之前需要对物理场进行初始设置 (预处理)。如果物理场在空间上变化,则可以使用不同的应用程序 (utility)来计算和预处理。有些应用程序是随 OpenFOAM 一起发布的 (例如 setFields 实用程序),或者是其它项目的一部分 (例如 swak 4 Foam 项目的 funkySetFields 实用程序)。
一些可用的预处理程序的使用将在第 8 章进行描述。
注:有关 swak 4 Foam 项目的更多信息可以在 http://openfoamwiki.net/index.php/Contrib/swk4Foam上的OpenFOAM wiki 上找到。
为了在数值上近似模型解,必须对模拟区域进行离散化。模拟域的空间离散化包括将区域分割成由不同形状的控制体积 (单元)组成的计算网格。所有这些控制体一起被称为“网格”或计算网格。通常情况下,在感兴趣的区域需要对网格进行细化:例如在出现较大的流场梯度的那些区域。此外,还必须注意数学模型的准确性和正确的选择。以空间的方式解析流动特征并不能补偿一个最初没有考虑这些特征的模型。
另一方面,瞬态模拟中增加网格分辨率可能会极大地降低模拟速度。这是因为当使用显式离散方式时,为了获得稳定的解,离散时间步长通常需要设置成较小的值。如果数值模拟不收敛,则网格可能是模拟中最有可能需要改变的部分。失败的模拟经常是由网格质量不足引起的。OpenFOAM 附带两个不同的网格生成器,即 blockMesh 和 snappyHexMesh。这两种网格生成器的用法都将在第 2 章中介绍。
此外,预处理还包括其他各种任务,例如,如果模拟是在多台计算机或 CPU 核心上并行运行,则要对计算域进行分解。
1.2.4 求解
除了网格生成外,计算求解通常是 CFD 分析中最耗时的部分。
计算求解所需的时间在很大程度上取决于数学模型、用于近似求解的数值格式以及计算网格的几何和拓扑性质。在这一步中,微分数学模型被 (线性化的)代数方程组所取代。在 CFD 中,这样的代数线性方程组通常很大,导致矩阵具有数百万或数十亿的系数。这些代数方程组是用专门为此开发的算法——迭代线性求解器来求解的。
OpenFOAM 框架支持选择多种线性求解器,尽管求解器应用程序通常有预设或理想的线性求解器和参数选择。熟练的 CFD 工程师有机会修改求解器和相应的参数。线性求解器和离散化策略的选择是影响计算速度和稳定性的重要因素。
1.2.5 后处理
在模拟成功完成之后,用户通常会有大量的数据需要分析和讨论。为了检查流动细节,必须适当地提取数据、绘制数据和/或可视化数据。通过使用诸如 paraView 之类的专用工具,可以相当容易地讨论这些数据。为了分析模拟结果,OpenFOAM 提供了广泛的后处理应用程序。
OpenFQAM 自带标准后处理工具 paraView。它是一个开源工具,可以从以下网站免费获得: www.paraview.org 。
1.2.6 验证和确认
用户必须自己决定是否信任计算结果。通常 CFD 软件非常复杂,其依赖于可配置的参数,这给错误留下了很大的空间。如果在前面的步骤中出现了错误,很有可能在验证和确认过程中被发现。
验证(Verification)保证了数值方法能正确地求解它所近似的数学模型。换句话说,验证检查数学模型的解是否被适当逼近。
确认(Validation)将仿真结果与实验数据进行比较:当涉及到仿真结果的置信度时,引入了更严格的安全系数。当与实验进行比较时,验证确保选择了正确的数学模型,其解充分反映了现实。如果模拟结果不满足要求,则必须重新进行之前的 CFD 分析步骤。
本节简要概述OpenFOAM中的有限体积法(Finite Volume Method,FVM)。关于有限体积法的更详细描述,读者可以参考一下相关文献:Ferziger和Peric(2002)、Versteeg and Malalasekra,Weller,Tabor, Jasak及Fureby、Jasak, Jemcov及Tuković、Moukalled, Mangani, Darwish, et al等。
OpenFOAM中非结构有限体积法离散步骤与1.2节中描述的CFD分析步骤有一定的关联。用于定义流体流动的物理属性(如压力、速度或温度/焓等)是数学模型(描述流体流动的偏微分方程组)中的相关变量。
看似不同的物理过程有时可以使用相似的数学模型进行描述,例如热传导过程与水中糖分浓度扩散过程都可以使用扩散模型进行描述。如Ferziger和Peric 2002所描述的通用标量输运方程中包含了用于模拟不同物理过程的项(微分算子),如:流体粒子随流体速度的输运(对流项)、热源(源项)等。由于通用方程中包含了经常遇到的项,因此常用其描述FVM的离散过程。通用输运方程为:
式中, 为待求标量; 为指定的速度向量; 为扩散系数。方程(1.1)中各项从左至右分别为:瞬态项、对流项、扩散项及源项。方程中的每一项都描述了一个以不同方式改变场变量 的物理过程。
有时可以根据物理过程的特性忽略一些项:如对于无粘流体流动,可忽略动量的扩散,因此可以将其从动量方程中去掉。此外出现在某些项中的系数可以是恒定值,也可以是空间和/或时间上变化的物理场,或与介质的物性参数有关。
数值方法的目的为了获取数学模型的近似解。对复杂物理过程进行近似求解是有必要的,因为精确求解通常只能在一些非常特殊的情况下才能得到,而这些特殊情况往往难以应用在工程实际中。
数学模型的近似解通过求解控制方程组的离散近似而得到。有限体积法(FVM)的近似过程涉及使用相应的线性代数方程组替代PDE系统,然后使用计算机进行求解。非结构有限体积法(FVM)生成代数方程组包括两个主要步骤:解域离散和方程离散。
1.3.1 解域离散
数学模型使用连续变量。为了逼近数学模型的解,空间被离散成有限数量的控制体积(网格单元)。这些有限体积(单元)构成了有限体积网格。
图1.1显示了从连续流体域到离散流体域的转变。
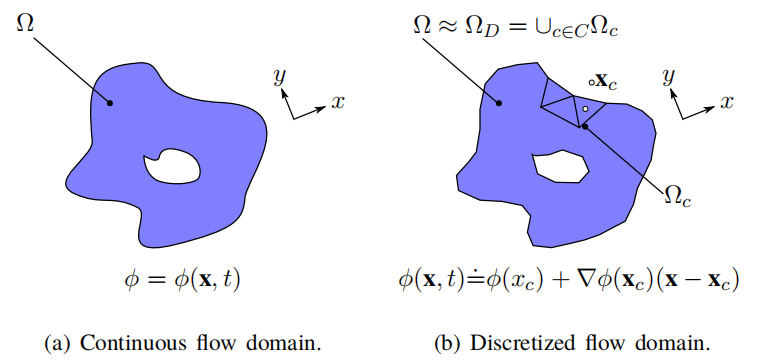
连续流体域近似为网格单元(有限体积)的集合:
其中,为有限体积网格,是离散区域中所有网格索引的集合。在图1.1a中流体填充的空间的每一点上定义的连续物理场在有限体积内被线性近似,如图1.1b所示。
每个有限体积都存储与其中心相关的物理属性(如温度)的体积平均值。将该值与网格中心相关联可使区域离散达到二阶精度。为了解为何会出现这种情况,可以假设物理场可以使用泰勒级数展开为:
引入在点 处定义的量(这些量在 上是恒定的),用式(1.3)中的泰勒级数展开表示网格 内部 的体积平均值,可得到:
体积域的中心定义为:
将式 到式 中,可得到:
由式 可知,对于线性分布的 ,由于其高阶导数为零,因此 在有限体积 上的平均值正好等于 在 的中心 处的值。换句话说,有限体积中心处的单元平均值(以网格为中心)可以准确地恢复线性物理场的值。能精确恢复线性函数值的方法至少具有二阶精度。
注:在网格的中心处得到的单元平均值的非结构FVM的区域离散具有二阶精度。
基于式 的变量 的插值:
式 具有二阶精度,因为式中泰勒级数截断部分的最大项与 成比例。
在式 中,网格中心处的梯度 也必须估计,计算方法在1.3.2节方程离散中会介绍。在理解方程如何离散之前,应当更详细地定义网格 ,特别是网格单元 的相互连接方式,因为这种连接性决定了哪些区域可以离散化。
我们在此区分三种类型的网格:结构网格、块结构网格及非结构网格。这三种网格对区域和方程的离散有不同的要求,并且网格单元相互连接和寻址方式也不同。网格单元之间的连接(网格连通性)决定了相邻单元的访问方式,这对于方程离散非常重要。这进一步影响了在访问网格单元时可能进行的优化,这些优化反映了数值运算的效率以及如何将这些运算并行化。
例如,网格单元的非结构化寻址使得很难在任何特定方向上访问网格单元。这使得在高阶插值格式所需的非结构化网格上构建更大的模板变得复杂,因为它们依赖于来自更宽邻域的单元平均(单元中心)值。使用域分解和消息传递方法对这种依赖单元中心值的高阶插值进行并行化也很复杂,而且可能效率不高,因为必须跨进程边界传递长度可变的大消息。因此,网格的连通性决定了在网格上可以有效地计算什么,有时会产生这样的效果:即为特定的网格选择错误的数值方法所造成的效率低下,使得该方法无法用于实际问题,而这些问题通常需要更多的网格单元。在OpenFOAM中,网格连通性在数值算法的实现方式中也起着非常重要的作用,OpenFOAM仅支持非结构化网格。
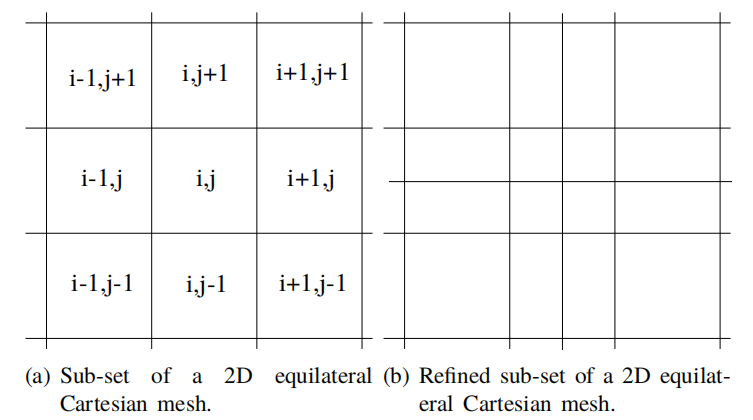
结构网格支持对任意网格单元的邻居进行直接寻址以及对网格单元的直接遍历:单元被标记为沿坐标轴方向递增的索引(参见图1.2a)。另一方面,非结构化网格没有明显的方向(见图1.3a)。
结构网格连通性提高了FVM中涉及的插值的绝对精度,但是当将其用于复杂几何区域的网格生成时,会使网格的灵活性降低。
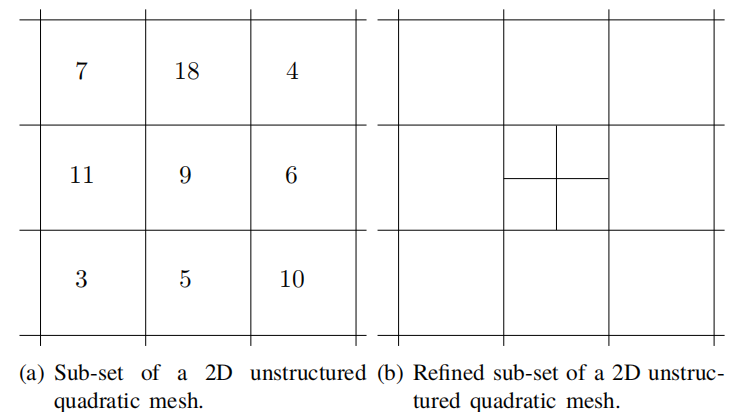
在网格生成过程中,用户通常希望在解发生较大变化的地方生成密集的网格,而不希望在变量梯度较小的流动区域中浪费网格。所有网格生成步骤应在最短的时间内完成,如果没有实质性的改善,使用结构化网格是无法实现此目的的。对结构网格进行局部网格细化是不可能实现的,因为网格细化必须通过整个网格传播到各自的方向。图1.3b给出了结构网格和非结构网格之间拓扑差异的示意图。
图1.2a显示了一个二维结构网格。这种网格也被称之为笛卡尔网格,因为其由体积中心沿坐标轴方向分布的控制体积组成的。通过改变索引在网格中移动具有一个显著的优势:使用这种网格的数值方法可以通过简单地将索引,递增或递减1来访问任何相邻的网格。例如当通过单元面的通量从单元中心插值到面中心时,可以轻松地应用高阶插值格式以提高求解精度。高阶插值格式意味着将更多的网格单元(不一定与当前网格相邻)包括在插值计算中。
但存在一个问题:在结构网格中进行网格局部细化是很难实现的。
当结构网格上可用的插值阶次仍然不够精确时,在极端变化的区域中常会出现这种情况。例如,在激波模拟或两种不相溶流体的两相流模拟中,会出现物性参数值的显著变化。将它们分开的两种流体之间形成了一个界面,物性参数值可能会存在几个数量级的变化(如气-水界面,密度比约为1000),如图1.4中的示意图所示。
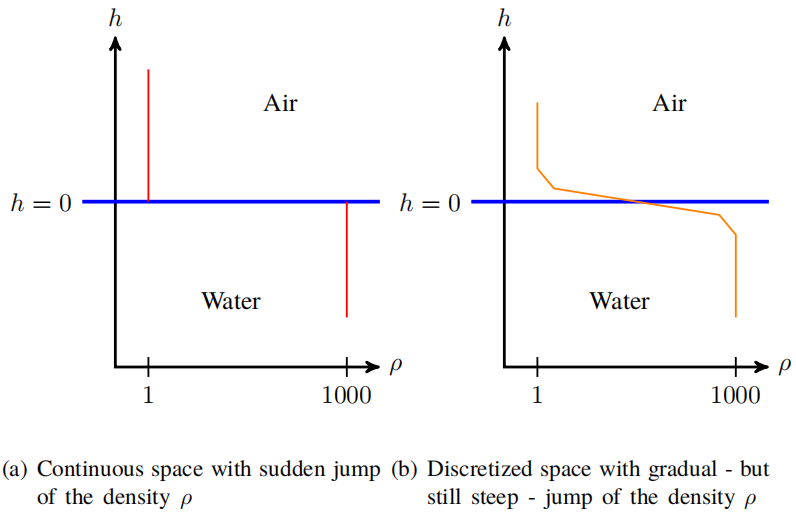
为求解这种数值的急剧变化,需要对网格进行局部细化。这种网格细化既可以在前处理期间完成,也可以在求解计算时进行。如前所述,结构网格的细化不能在局部完成:结构化网格的拓扑结构迫使网格在整个方向上进行细化(请参见图1.2b),其中在两个方向上对单个网格的细化会在整个方向上产生细化。符合弯曲几何形状的结构化网格尤其难以生成,为保持结构网格的连通性,必须对弯曲边界进行参数化,这仅适用于相对简单的几何边界。
然而,结构网格离散在实际应用中有一些扩展,其中一些扩展允许对网格进行局部和动态细化。为了提高局部精度,可以使用块结构细化,这是一个构建由多个结构块组成的网格的过程。当组装这样的块结构网格时,不同的块可以具有不同的网格密度。不幸的是,这引入了新的复杂性,因为数值方法必须能够处理不一致的悬挂节点。或者通过精心地处理结构块,以使不同密度的相邻块上的网格节点完全匹配。即使对于简单的流体域,构建块结构网格也是一个复杂的问题,这往往使得在许多涉及复杂几何形状或边界形状的技术应用中,块结构的网格都不是一个好的选择。细化块结构的网格会导致细化区域扩展到整个块中。使用依赖于边界一致性的块结构网格的标准求解器,细化会使得网格生成更加复杂。
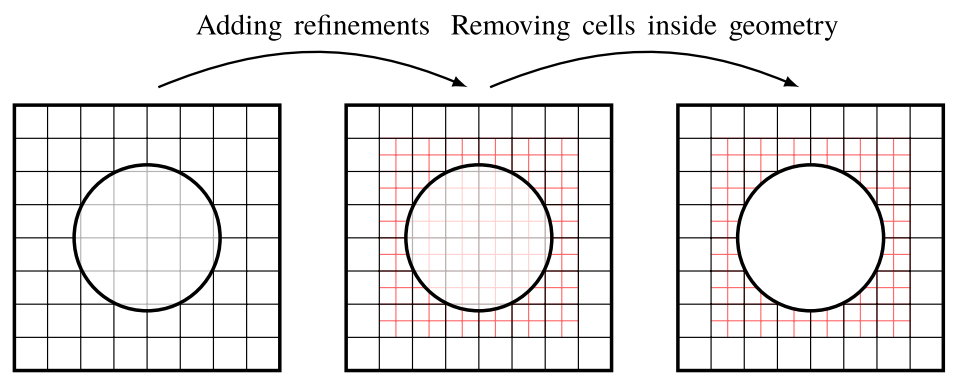
OpenFOAM中的动态自适应局部细化是通过引入额外的数据结构来实现的,这些数据结构产生并存储与网格细化过程相关的信息。这种方法的其中一个例子是基于八叉树的细化,其利用八叉树数据结构将每个结构笛卡尔网格元拆分为八个。这种方法要求网格(或至少是正在细化的网格子集)仅由六面体单元组成。数值插值程序(离散微分算子)使用八叉树数据结构存储信息,并考虑局部网格细化导致的网格拓扑变化。然后可以使用切割单元方法将处理更复杂几何域的可能性添加到八叉树精细结构网格中。在这种情况下,通过边界的分段线性近似来切割弯曲域边界的网格。基于八叉树的自适应网格细化在效率方面具有优势,这取决于在底层结构化网格上执行拓扑操作的方式。然而基于八叉树的细化逻辑要求细化域必须是盒形的。更多关于局部自适应网格细化程序的信息可以在[文献](8 “Tomasz Plewa, Timur Linde, and V Gregory Weirs. Adaptive mesh refinement-theory and applications. Vol. 41. Springer, 2005, pp. 3–5.”)中找到。
OpenFOAM实现了一个支持任意非结构网格的二阶收敛的FVM。除了非结构化网格的连通性之外,任意非结构网格的单元可以是任何形状。这允许用户对几何复杂度非常高的流体区域进行离散。非结构网格允许非常快速、有时甚至是自动的生成,这对于工业应用来说非常重要,因为在工业应用过程中需要尽可能快速地获得结果。
图1.3a显示了一个二维非结构网格。由于网格寻址不是结构化的,所以仅出于解释网格连通性的目的对单元进行了标记。无序的网格单元使得在特定方向上执行操作变得更加复杂,但无需执行昂贵的额外搜索及在局部重新创建网格方向信息。非结构网格的另一个优点是能够直接对网格进行局部细化,如图1.3b所示。局部细化在控制网格密度方面更为有效,因为它只在需要时提高网格密度。
注:OpenFOAM中的网格连接是完全非结构的。对于简单几何区域,常使用blockMesh以块方式生成网格,但这并不意味着会生成块结构网格。
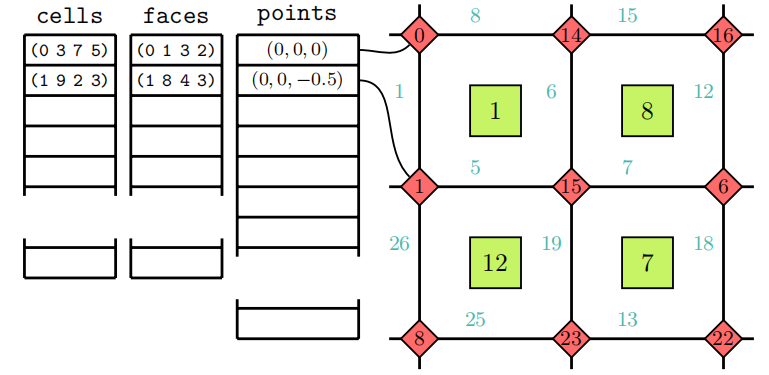
数值算法对网格单元的寻址方式屈居于网格的连接性。OpenFOAM依靠Indirect addressing、Owner-neighbor addressing和boundary mesh addressing来寻址网格单元。
1. Indirect addressing
Indirect addressing(间接寻址)定义了如何从网格节点组装网格,其中网格以全局点列表的形式给出。网格面使用整数标签对全局网格节点列表进行索引。这样在构造网格面时,不需要重复点的坐标,从而能够节省内存,并提高计算效率。因此,每个网格面都是全局网格节点的整数索引列表。网格中的所有网格面都存储在一个全局面列表中(一个索引列表的列表)中,这就是间接寻址这个名称的含义。类似地,网格也被构建为索引列表,用于寻址全局面列表中的面的位置,如图1.5所示。与网格面一样,网格单元也存储在全局(单元)列表中。如图1.5所示的面1就是一个例子,它是由点0和点1以及图中未显示的点3和点2构成的。该面又被用于组装单元1。用于网格面和网格单元的间接寻址可避免在创建网格面或单元的实例时复制网格节点,否则在内存中会存储多个相同网格节点和网格面的副本,这将浪费计算能力,并会使数值和拓扑操作严重复杂化。
2. Owner-neighbor addressing
Owner-neightbor寻址定义哪个网格拥有某个面,哪个网格是该网格面的邻居网格。此外它还优化了对网格面的访问。当使用二阶精度的非结构FVM离散输运方程时,离散由每个网格面上的总和组成,且在每个网格面的中心使用插值。由于相邻网格共享网格面,每个网格面的离散计算会导致在两个网格共享的网格面上执行两次相同的计算。为避免出现这种情况,在网格中引入两个全局列表:face-owner列表和face-neighbor列表。每个网格面最多由两个网格共享。由于网格存储在全局网格列表中,因此它们由其在该列表中的位置索引(cell label)唯一标识。具有较小索引的网格成为与具有较大索引的网格共享的面的owner网格。在图1.6中,面的owner网格用标记,与面相邻但具有较大网格索引的另一个网格称为face-neighbor,其在图1.6中用标记。面区域法线向量的方向如图1.6中的箭头所示。面法向量总是从owner指向neighbor,从索引较小的网格指向索引较大的网格。这样,不是在所有网格单元上离散计算,而是在所有网格面上只计算一次。然后,按照外向法线面积向量的约定,通过离散的微分运算操作将面中心处的贡献加到owner上,并从neighbor中减去。
3、Boundary addressing
Boundary addressing(边界寻址)负责处理边界网格面的寻址问题。根据定义,所有只有一个owner网格且没有neighbor的网格面都是边界面。为提高效率,边界网格面存储在网格面全局列表的末尾,并组合为patch。 将边界网格面分组为边界patch与应用边界条件有关,对于不同的边界面组,边界条件会有所不同。因此,完整的边界网格定义为边界面列表。这允许高效地将边界面定义为全局网格面列表的子集。边界网格的这种定义导致OpenFOAM中依赖于基于网格面的插值实践的所有顶层代码的自动并行化。因为它们只有一个网格owner,所以边界网格的所有法向量都指向计算域的外部。
虽然间接寻址和非结构化网格连接增加了处理复杂几何体和应用局部优化的灵活性,但间接寻址是有代价的。与结构网格代码相比,间接寻址降低了代码的性能。
图1.6显示了面owner-neighbor寻址机制如何对非结构网格的体心值寻址的示意图。为每个网格面定义索引对,该索引对包含与面相邻的网格和的索引及。具有较小网格索引的面相邻网格称为的所有者网格(Owner),具有较大索引的网格称为所谓的相邻网格(Neighbor)。索引标记网格1的边界面,边界面只有一个owner网格:网格1本身。
OpenFOAM中的非结构网格也存储了其他的寻址,如单元单元和网格节点。附加寻址可以用来构造不同于非结构FVM的、需要不同网格单元连通性的数值方法。
时间被认为是求解域的附加维度,时间间隔被离散为分区,其中,差值称为时间步长,是前一个时间点,是当前时间点,是下一时间点。
1.3.2 方程离散
一旦求解域被离散为有限体积,就可以对数学模型中微分算子()的项进行近似,将其转化为方程 中的离散微分算子。非结构 FVM 的离散微分算子表示为网格中心平均值(由式 )计算)的线性组合,换句话说,它们是以网格中心值为因变量的线性代数方程组。由于网格 的偏微分方程的离散过程将离散形式的 PDE 表示为其相邻网格中心值的线性组合,因此相邻网格会影响网格 中的解。由于这是针对每个网格 进行的,所以离散得到基于网格 和 的全局代数线性方程组,然后求解 。下一节将介绍如何使用非结构 FVM 方程离散来实现这一点。
非结构化FVM的其他描述可见[文献](6 “F Moukalled, L Mangani, M Darwish, et al. The finite volume
method in computational fluid dynamics. Springer, 2016.”)和[文献](2 “Charles Hirsch. Numerical computation of internal and external flows: The fundamentals of computational fluid dynamics. Elsevier, 2007.”)。OpenFOAM中非结构FVM的公开描述可以在[3](3 “Jasak. “Error Analysis and Estimatino for the Finite Volume Method with Applications to Fluid Flows”. PhD thesis. Imperial College of Science, 1996.”),[5](5 “F. Juretić. “Error Analysis in Finite Volume CFD”. PhD thesis. Imperial College of Science, 2004.”),[12](12 “O. Ubbink. “Numerical prediction of two fluid system with sharp interfaces”. PhD thesis. Imperial College of Science, 1997.”),[9](9 “Henrik Rusche. “Computational Fluid Dynamics of Dispersed Two-Phase Flows at High Phase Fractions”. PhD thesis. Imperial college of Science, Technology and Medicine, London, 2002.”)等文档中找到。
方程 的所有项都需要离散才能得到代数方程。数值方法必须是一致的(见[1](1 “J. H. Ferziger and M. Perić. Computational Methods for Fluid Dynamics. 3rd rev. ed. Berlin: Springer, 2002.”)):随着网格尺寸的减小,离散(代数)数学模型必须接近精确的数学模型。也就是说,无限细化计算域并在此空间离散上求解离散模型,可以得到由偏微分方程组成的数学模型的解。为了获得离散模型,在网格区域 上对方程 进行积分:
回想一下式 中给出的与 中心相关的二阶精度体积平均值:
1.3.2.1 时间项
利用式 对式 中的时间项进行离散化,并对网格中心值使用速记符号 ,可得到空间二阶精度离散:
然后可以使用有限差分来近似时间项。在OpenFOAM中,可以使用first-order backward Euler(Euler)或second-order backward difference二阶精后向差分(BDS2)格式,即
式中,为新的时间步,为当前时间步,为前一时间步。最后,使用由式(1.11)给出的二阶精度后向差分格式(BDS2),时间项被离散为:
1.3.2.2 散度(对流)项
利用散度定理对方程(1.8)中的进行离散:
方程(1.13)中解域的边界是由线段(几何边)限定的并集面,即有:
式中,为网格域的面的索引。式(1.1.3)可写为:
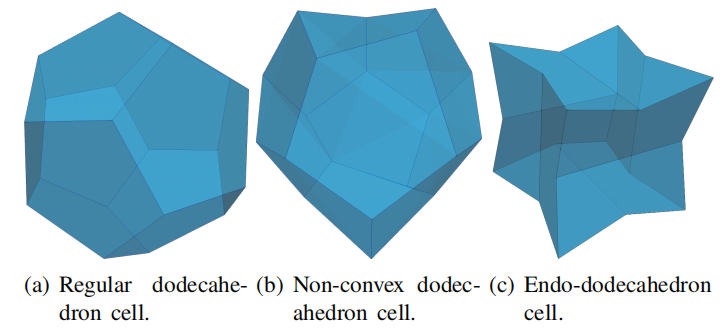
若网格为凸多面体(四面体、立方体、长方体等),则网格的网格面为平面多边形,如上图1.7a中所示的十二面体。或者可以是“广义多面体”:由面围成的非凸体,这些面既可以是非平面,也可以是平面且非凸的面。例如,图1.7b中的非凸十二面体是非凸的,原因很简单,因为它的面不是平面。图1.7c所示的内十二面体是非凸的,因为它的面虽然是平面,但却是非凸的。多面体网格生成算法通常创建非平面多面体,如图1.7b所示。此多面体的面是以直线段(网格边)为边界的非线性直纹曲面。这在图1.7b中的非平面多面体的顶面清晰可见。内十二面体对于多面体网格的生成并不那么重要,尽管理论上它可以出现在十二面体网格中。为了避免在离散过程中引入特殊情况的处理,OpenFOAM中将所有的网格视为广义的多面体。通过使用每个多边形面的质心将面分解成一组三角形来线性化所有的网格面。当网格确实是凸多面体时,这当然不会引入误差。如果是具有非平面面的广义多面体,则使用基于质心的三角剖分对其面进行三角剖分会在方程式(1.15)上引入逼近误差。
为了进一步离散式(1.15),通过应用由式(1.7)给出的平均的2D等效函数,对每个面进行的平均,在面的质心处:
其中,。将方程(1.16)插入式(1.15)可得到:
由等式(1.1)给出的散度项的空间二阶精度离散。在OpenFOAM中,使用所谓的同位离散(collocated discretization):线性代数方程组中的所有因变量都存储在网格中心。因此,使用存储在每个面的两个面相邻网格中心处的值来表示等式(1.17)上的面心平均值。
注:非结构FVM中,面心平均值相当于体心值,具有二阶精度。
应用于正交三角形网格的中心差分插值格式如下图所示。
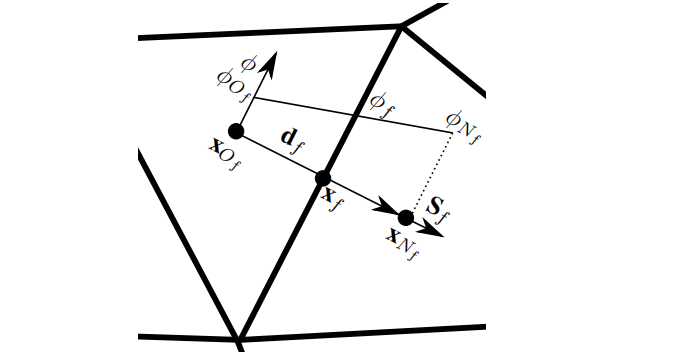
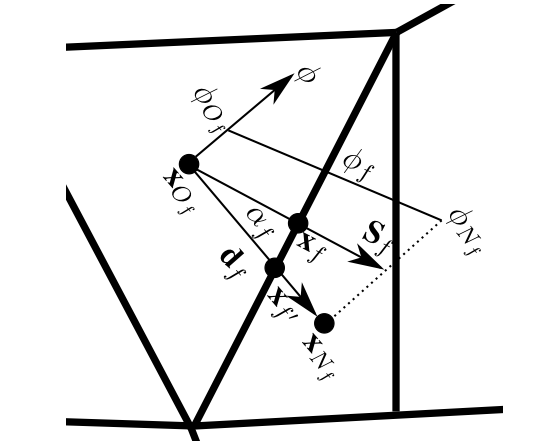
考虑图1.8所示的2D三角形网格上的面f及其两个相邻的所有者网格和相邻网格,如果以面心值使用线性插值(中心差分格式,CDS)表示的,就有:
式中,;OpenFOAM中所谓的delta系数;为通过CDS格式计算的线性面系数:
面系数 , 也可以使用迎风格式进行计算,对于对流项,可以使用存储在上游网格体心上的值来定义:
式中,为出的标量体积通量:
若指定了速度,则其不是方程(1.1)中的因变量,并且其在方程(1.17)中的表达方式与完全相同,使用线性插值(CDS)或方程(1.19)中面相邻值的其他组合。
将面心平均值计算为来自相邻网格的单元中心值(例如通过CDS方程(1.18))以及来自方程(1.22)的标量体积通量的组合,可以得到离散散度算子为:
式中,为属于网格的owner面的索引集。
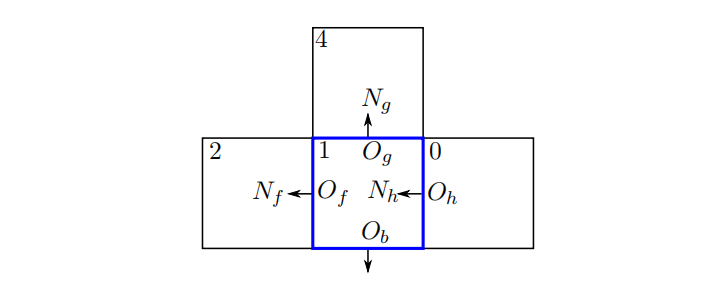
到目前为止,没有对网格边界的法向量的方向(即网格的网格面的法向面积向量的方向)作出任何假设或离散。然而,OpenFOAM不会使用网格所有面上的和(索引集)来离散方程(1.1)(方程(1.8))中的散度/扩散微分算子项,也不会在OpenFOAM中为每个网格一致地确定其边界的法向量方向(仅向外或仅向内)。对于每个网格面中心,定义唯一的向量。这妨碍了法线的一致性,因为对于与面相邻的网格,必须向内。
离散散度算子在OpenFOAM中通过使用owner-neighbor寻址实现。向量为式中从owner单元指向neighbor单元的面法向向量,这是OpenFOAM中非结构FVM的一个非常重要的实现。
散度定理假设方程 (1.13) 中边界 的法线方向一致:法线 可以相对于单元 向外或向内,并且在OpenFOAM中使用法向方向向外的约定。等式 (1.23) 对散度项的离散化导致网格的所有面的总和。如果要对每个网格执行离散化,则强制法线方向的一致性会很复杂。例如,对于图 1.6 中的网格 1,由于所有者-邻居寻址,单个面区域法线向量方向向内。以任何其他方式定义唯一的法线向量 Sf 仍会使该向量从一个网格指向另一个网格,有效地指向其中一个网格。onwer-neightbor寻址用于第 1.3.2 节中介绍的域离散化,因为它根据面相邻网格的索引唯一地确定法向方向:owner网格的索引小于neighbor网格。
所以问题是:如果网格(图 1.6 中的网格 1)的一些面朝外而有些面向内,如何进行方程(1.23)给出的散度项的离散化?
由于向量总是从具有较低索引的网格 (face-owner, owner-cell, owner) 指向具有较高索引的网格 (face-neighbor, neighbor-cell, neighbor),因此对r.h.s.总和的贡献被添加到owner面,并从面 的neighbor中减去。为了实现这一点,引入了两个索引集:owner(owner-cell ) 和neighbor(neighbor-cell)索引集,即
由等式(1.24)和(1.25)给出的索引集O、N分别包含网格中每个面的所有者和邻居单元的标签,而不是像等式(1.23)中的索引集Fc那样包含单元的每个面的所有者和邻居单元的标签。这使得即使当单元的法向量SF不都指向外部或内部时,也可以执行与等式(1.23)中相同的计算。
对于所有,有:
其中F为网格中所有面的索引几何,为由方程(1.24)给出的面owner单元从O中得到的索引,为由方程(1.25)给出的面相邻单元n的索引,为由方程(1.23)给出的离散散度算子。
注:方程(1.23)对散度算子的离散有助于理解非结构化有限体积法,而OpenFoam中的实际计算则是用方程(1.26)进行的。
注:可以使用FVMesh类的owner()和neighbour()成员函数从网格访问所有者和邻居索引集。
如第1.3.1节所述,并在单元格1的图1.6中所示,边界面只有一个所有者-单元格。 因为这个面没有邻居单元,所以在等式(1.26)中它不会有贡献。 为了避免检查面是否属于网格边界,边界面(图1.6中的B面)在OpenFoam中与内部面分开存储。
1.3.2.3 Laplace(扩散)项
方程(1.1)中的拉普拉斯(扩散)项与散度(对流)项相似地离散化。 离散从上的积分和散度定理的应用开始,使用速记符号,可以得到:
其中空间二阶精度误差项是由方程(1.16)给出的面内平均产生的。
拉普拉斯项离散的下一个步骤是梯度的离散。 方程(1.27)中的面心梯度不是从面相邻网格中心梯度中插值得到的。取而代之的是,泰勒级数从面中心到owner,以及到neighbor网格中心都被使用。 为了简化表达式,引入了以下速记表示法。 对于面心值,使用(等价于),此外还使用向量的张量积表示法:
利用这种表示法,从面心、面owner和neighbor分别给出泰勒级数为:
从式(1.29)减去式(1.28)得到:
在等距网格上,类似于图1.8中所示的网格,面中心将向量分解成两个相等的部分,这样
将方程(1.31)代入方程(1.30)中,乘以,除以,就可以消除方程(1.30)中的二阶项,即:
这导致面心梯度的最终离散为:
方程(1.33)只在满足方程(1.31)的等距网格上,并且对于可展开为泰勒级数的足够规则的,证明了面心梯度在项中的二阶精度,但只有在满足方程(1.33)的等距网格上才具有二阶精度。 如果方程(1.31)不成立,则方程(1.33)中的最大误差项包含来自方程(1.30)的贡献,这使得离散具有一阶精度。
在预计φ发生强烈变化的区域,宽高比应为理想的0.5,因为这样方程(1.31)成立,并实现了方程(1.33)的二阶精度离散。 在不足够小且对求解的二阶收敛几乎没有影响的情况下,可以使用更强的网格分级。
考虑图1.9:在垂直方向上变化很大,边界层捕捉到了的垂直变化。 然而,边界层在停止之前结束时变化很大,并且由于长宽比不等于0.5,在用表示的面上的梯度离散引入了一阶误差项。 另一方面,在图1.9中没有任何水平变化,因此不等于0.5的纵横比实际上对这些面的求解精度没有影响。
利用方程(1.33)对进行二阶精度离散,通过将方程(1.33)代入方程(1.27)来确定Laplace项的离散,得到Laplace(扩散)项的二阶精确FVM离散:
如果和共线(),或者换句话说,如果网格是正交的,方程(1.34)对Laplace项的离散可以进一步简化,如
图1.10中显示了一个非正交网格:在一个非正交网格中,在面处,向量不共线,形成一个所谓的非正交角。 非正交性在方程(1.35)中引入了一个误差,基于高斯散度定理,利用网格中心梯度的离散来校正这个误差。 网格质心处的梯度可以离散为
二阶精度由方程(1.16)中的面心平均和方程(1.18)中的线性插值给出。 在网格质心处以这种方式离散的梯度用表示。 如果方程(1.36)与方程(1.18)在面中心处线性插值,即
由于线性插值是有界的,面心梯度保持了方程(1.36)给出的owner及neighbor梯度的二阶精度,这意味着它保持了和网格的误差的界。 在方程(1.36)中,二阶精度项简化为:实际上,在一般非结构网格上,该表达式更为复杂。 该误差可以用最大误差来粗略估计,如及,其中是所有面点的集合。 最后,在方程(1.31)给出的条件下,即使,以网格为中心的高斯梯度的线性插值仍保持二阶精度。
用方程(1.36)近似的面心梯度在方程(1.27)中不用于拉普拉斯项的离散,因为方程(1.37)会引起所谓的棋盘网格。 棋盘网格是指在某些情况下,由于方程式(1.37)中存在的人为抵消,离散无法计算。 作为一个最简单的例子,考虑五个用(0,1,2,3,4)标记的一维有限体积网格,它们之间有一个单位距离,在它们的网格中心有(50,100,50,100,50)的分布。 如果使用公式(1.18)和(1.36)计算以网格为中心的梯度及,以及基于owner-neighbor寻址的法向量定向(分别为),则所得梯度为和。 这些假零点,通过方程(1.37)进一步插值以计算面心梯度及保持零值。
或者,如果用公式(1.37)计算,则有,同样适用于。 这个例子显然是人为的,但它表明离散忽略了两个相邻网格之间求解的振荡,这种振荡虽然不像这个例子中那样有规律,但实际上可以是求解的一部分。 这种振荡的一个例子是压力中由一系列小的(未解析的)涡旋引起的振荡。
方程(1.37)不使用面心梯度,因为它会导致棋盘式。
由方程(1.37)给出的线性插值面心梯度可以用来校正方程(1.35)中的非正交性。 通常用于表面积法向量分解的方法有三种:最小校正法、正交校正法和过松弛校正法。 三种方法都将面积法向量分解为与共线的正交部分和非正交部分,
这样:
图1.11给出了不同的的计算方法,并根据方程(1.39)计算了\mathbf{S}_f^\cancel{\perp}。 用方程(1.33)计算方程(1.40)中的梯度的正交贡献,该方程包含两个面相邻网格的平均值,并采用隐式离散化。非正交项贡献(\nabla \phi)_f^\cancel{\perp}采用显式离散。
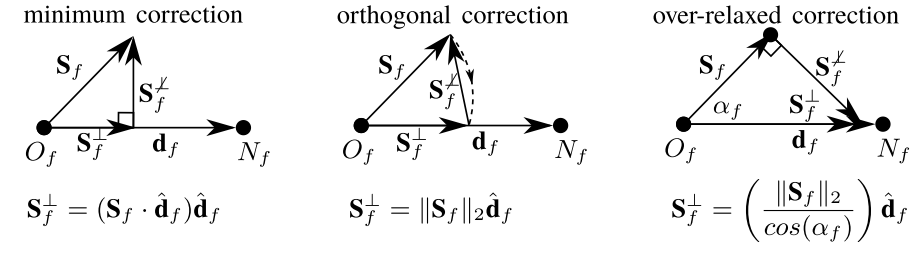
对方程(1.40)中(\nabla \phi)_f^\cancel{\perp}的显式离散结果为:
这是不成立的,因为正交和非正交贡献是在不同的时间步长上评估的。 为了修正方程(1.40)中和之间的差异,在OpenFoam中使用在每个时间步长内附加固定数目的附加迭代进行非正交修正,即
希望经过次迭代后,。 非正交校正的迭代在压力-速度耦合算法中起着至关重要的作用,其中拉普拉斯算子用于压力的泊松方程。 这就是为什么OpenFoam中的pressure velocity耦合算法的配置文件有一个适当的条目。
注:
- 在 OpenFoam 中,用于压力泊松方程的非正交性校正的迭代次数 可以在 System/FVSolution 配置文件中设置。
- CheckMesh应用程序报告了非结构OpenFoam网格中的非正交角信息。
- 在一般情况下,如果网格是非正交的,也是非等距的,此时方程(1.31)不成立,在面心处的梯度近似变成一阶精度。
通常,网格非正交性将和之间的交点(图1.10中的点)从面中心移开,用于方程(1.16)中的平均。 方程(1.16)期望面平均值与面中心相关联,以确保二阶精度,并且由于是插值实际发生的地方,因此引入了所谓的网格偏斜误差。
注:如果方程(1.16)中用于面上平均的面中心不对应于交点,则会引入网格偏度误差。
在科学文献中提出了不同的解决偏斜误差的方法,但目前在OpenFoam中没有任何偏斜校正方法是可用的,因此这里不详细讨论偏斜误差。 关于非结构FVM的非正交性和偏度误差的附加信息可以在[3,5,6]中找到。
1.3.2.4 时间离散
时间离散结合了迄今为止所描述的时间、对流(散度)和扩散(拉普拉斯)项的离散。 使用到目前为止描述的离散化算子重组离散化标量输运方程(1.1),我们可以写
用泰勒级数对进行时间展开,以为时间步长,得到:
且有:
由方程(1.44)和方程(1.46)给出的离散化是等价的,并且具有同等的一阶精度。 然而,OpenFOAM使用方程(1.46)给出的隐式欧拉离散,因为它对于初始条件光滑的线性方程组是无条件稳定的。
将方程(1.46)插入方程(1.42)中,得到了标量输运方程(1.1)的离散,采用了常用的隐式欧拉格式,该格式在时间上具有一阶精度,在空间上具有二阶精度:
其中源项要么在旧的时间步处求值,要么在和时间处使用线性外推。 关于源项线性化的附加信息可以在[7]中找到。 或者,将方程(1.44)插入方程(1.42)并将所得方程与方程(1.47)求和,得到Crank-Nicolson格式:
这在时间上也是二阶精度,因为项和分别在方程(1.44)和方程(1.46)的求和中抵消,留下作为前导截断项。 验证这一点留给读者做一个简短的练习。
OpenFOAM中应用CreakNicolson格式,可以在system/fvSchemes文件中设置:
ddtSchemes
{
default
CrankNicolson 0.5;
}
在OpenFOAM中,Crank-Nicolson格式中的系数0.5是通过将隐式和显式项组合在一起而变的,即:
当时,从方程(1.49)恢复方程(1.48)。 如果用方程(1.46)表示得到方程(1.47)给出的一阶欧拉隐式方法。
在仿真案例中,在仿真文件夹的System/fvSchemes字典中选择时间积分格式,如清单所示,其中使用。 当然,方程(1.49)中的源项是的线性化函数,这保证了一个线性代数系统是由方程离散得到的,可以用线性求解器求解。
ddtSchemes
{
default
CrankNicolson 0.5;
}
1.3.2.5 线性代数方程组
用方程离散法构造了一个线性代数方程组,求解了网格中每个网格中的。 例如,考虑由方程(1.48)在正交网格上给出的离散。 项和将分别依赖于方程(1.35)和方程(1.23),从时间步长中,将来自网格C的面的值引入方程(1.48)。 其他项,如只包含当前和新时间步长的值。 从网格C和它的面邻居集合中分离贡献,得到一个线性代数方程,通常写为
隐式离散,如公式(1.48)所示,为网格中的每生成一个线性代数方程(1.50)。 方程式1.50是相互耦合的,因为在方程式中,对于每一个单元,都有来自相邻网格的贡献。 然而,由于贡献仅来自于与单元共用一个面的相邻单元,方程组将只有几个非零系数,由此得到的线性系统将是稀疏的。 求解稀疏线性代数系统的结果是对于新的时间步长计算网格中的每一个值,
1.3.2.6 边界条件
当一个面心值属于作为网格边界一部分的单元面时,在离散中需要边界条件。 所谓的边界面不具有相邻单元格,相邻单元格的值参与离散。 相反,定义的内容通常是:
- 值由Dirichlet或固定值边界条件指定
- 梯度由Neumann边界条件指定
- 或者一个值和梯度的线性组合是由混合边界条件或Robin边界条件指定
无论离散的隐式或显式性质、用于的插值格式或用于的梯度离散格式,边界条件在边界面上都是必要的。 图1.12中的粗线突出了边界面。
例如,用方程(1.48)组合线性代数方程方程(1.50),离散化算子所用的求和在某些单元中会遇到边界面。 让我们考虑对流算子,假设这样的边界面用标记,那么显然,离散对流项中的和应该加上。 对于内部面,该值将在与面b相邻的网格的以网格为中心的值之间插值。 但是,边界面旁边只有一个网格,根据定义,这个网格是那个面的owner。
对于FixedValue边界条件,过程很简单: 边界条件指定了属性的取值,速度的取值。这对于定值边界条件就足够了,但这使边界条件的实现变得非常复杂。 网格中的绝大多数面是内部面,而不是边界面。 因此,将内部面和边界面以某种方式混合在一起并加以分类是没有意义的,这样离散就可以“询问每一个面”它是否属于边界,以及另外为这个面规定了哪一个边界条件。 为了避免这一复杂情况,网格的面被分成内部面和边界面。 在OpenFOAM中,边界面被进一步分组为边界Patch:应用相同边界条件的边界网格子集。 这是有意义的,因为模拟过程通常有暴露在不同条件下的表面。 以传热为例:有些表面可以被隔离,有些表面可以通过流动的空气或液体喷雾冷却,有些表面将邻近由不同材料制成的物体。 因此,如图1.12所示,OpenFOAM中的物理场被分为内部(以细胞为中心的)物理场和边界面为中心的物理场,分为与特定边界斑块(边界条件)相对应的斑块物理场。 由于离散化算子中求和的方法可以分别应用于区域的内部和边界,因此,将面和边界分别划分为内部和边界块以及物理场,从而大大简化了OpenFOAM中的离散。
另一个边界条件是Neumann或“自然”边界条件,它规定区域边界处的性质梯度为零:
因此,在零梯度边界条件下,边界面上的值取自网格中心的值,即
对于边界面b上的零梯度边界条件,对代数方程方程(1.50)的边界贡献将以新时间步长中的单元值旁边的系数结束:方程(1.50)中的。 换句话说,零梯度边界条件将影响边界块下一个单元的线性代数方程组的对角线系数。 在OpenFOAM中实现了各种边界条件,它们要么指定了边界值,要么指定了梯度,或者指定了两者的组合。
1.3.2.7 解线性代数方程组
求解由非结构化FVM生成的线性代数方程组(线性方程组)通常需要大量的计算工作,因为它的大小为,其中是网格中的网格数,d是空间维度。 因此,方程(1.50)中旁边的系数是稀疏矩阵中的系数。 OpenFOAM使用一种特定的矩阵表示格式,以及一组与OpenFoam矩阵格式紧密耦合的线性求解器。 这里没有涉及这个主题,相反,读者可以参考[6,第10章]了解关于OpenFOAM矩阵格式和线性求解器的详细信息。 请注意,除了许多教程中的配置之外,很少需要对OpenFOAM中的线性求解器配置进行重大调整或修改。 文献[11]提供了共轭梯度线性求解器的一个信息和直观的推导。 关于稀疏线性系统的迭代求解方法的详细背景知识可在[10]中获得。
OpenFOAM由许多不同的库、求解器和实用程序组成。为了对这个庞大且经常令人生畏的代码库有一定的了解,我们可以查看一下OpenFOAM根目录的内容。
OpenFOAM目录的内容:
- application:求解器、实用程序和辅助测试函数的源代码。解算器代码按其功能进行组织,如
incompressible、lagrangian或combustion。实用程序被类似地组织为mesh、pre-precessing和post-precessing等类型。 - bin:Bash脚本(不是C++二进制文件),具有广泛的功能:检查安装(foamInstallationTest),在调试模式下执行并行运行(mpirunDebug),生成空源代码模板(foamNew)或case模板(foamNewCase)等。
- doc:用户文档、编程文档和Doxygen生成文件。
- etc:编译和运行时可选配置控制整个库的标志。
/etc/bashrc中设置了许多安装设置,包括使用哪个编译器、编译哪个MPI库以及安装的位置(用户本地或系统范围)。 - platforms:根据精度、调试标志和处理器体系结构存储的编译后的二进制文件。大多数安装在这里只有一个或两个子文件夹,这些子文件夹将根据编译类型命名。例如,linux64GccDPOpt可以解释为:
- linux:操作系统类型
- 64:处理器体系结构
- Gcc:使用的编译器(GCC、icc、clang)
- Dp:浮点精度(双精度(DP)与单精度(SP))
- Opt:编译器优化或调试标志
- src:工具包的大部分源代码。包含所有CFD库源,包括有限体积离散化、输运模型和最基本的原始结构,如标量、向量、列表等。Applications文件夹中的主要CFD解算器使用这些库的内容来运行。
- tutorials:工具包的大部分源代码。包含所有CFD库源,包括有限体积离散化、传输模型和最基本的原始结构,如标量、向量、列表等。Applications文件夹中的主要CFD解算器使用这些库的内容来运行。
- wmake:基于bash的脚本wmake是一个配置和调用C++编译器的实用程序。使用wmake编译求解器或库时,来自make/files和make/options的信息用于包括头文件和链接其他支持库。使用wmake需要make文件夹,因此编译大多数OpenFOAM代码都需要make文件夹。
第五章从软件设计的角度对OpenFOAM库进行了深入的描述,解释了C++编程语言的不同范型,以及如何使用它们来使OpenFOAM成为一个模块化的、功能强大的CFD平台。
OpenFOAM CFD框架通常看起来令人望而生畏,因为它要求用户对物理、数值和工程有扎实的理解。OpenFOAM是开源,因为解决方案过程的许多方面都向用户公开(这与商业模拟产品中常见的不透明形成对比)。对源代码的访问使用户能够根据自己的需要调整内容。然而,这种能力是以学习如何在Linux操作系统中使用命令行、学习定义非结构化有限体积法使用的参数的配置文件等为代价的。 理解本章是成功使用 OpenFOAM 的第一步。了解 OpenFOAM 中的非结构化有限体积方法,不仅对于开发新的方法,而且对于充分理解在某些模拟中可能出现问题的原因以及如何修复它,都是至关重要的。本书其余部分介绍的 OpenFOAM 的所有元素,如边界条件、离散格式、求解器应用程序等,都基于非结构化有限体积方法。
- J. H. Ferziger and M. Perić. Computational Methods for Fluid Dynamics. 3 rd rev. Ed. Berlin: Springer, 2002.
- Charles Hirsch. Numerical computation of internal and external Flows: The fundamentals of computational fluid dynamics. Elsevier, 2007.
- Jasak. “Error Analysis and Estimatino for the Finite Volume Method With Applications to Fluid Flows”. PhD thesis. Imperial College of Science, 1996.
- Hrvoje Jasak, Aleksandar Jemcov, and Željko Tuković. "Open FOAM: A C++ Library for Complex Physics Simulations". In: Proceedings of the International Workshop on Coupled Problems In Numerical Dynamics (CMND 2007) (2007).
- F. Juretić. “Error Analysis in Finite Volume CFD”. PhD thesis. Imperial College of Science, 2004.
- F Moukalled, L Mangani, M Darwish, et al. The finite volume Method in computational fluid dynamics. Springer, 2016.
- Suhas Patankar. Numerical heat transfer and fluid flow. CRC Press, 1980.
- Tomasz Plewa, Timur Linde, and V Gregory Weirs. Adaptive mesh Refinement-theory and applications. Vol. 41. Springer, 2005, pp. 3–5.
- Henrik Rusche. “Computational Fluid Dynamics of Dispersed Two Phase Flows at High Phase Fractions”. PhD thesis. Imperial college Of Science, Technology and Medicine, London, 2002.
- Yousef Saad. Iterative Methods for Sparse Linear Systems, Second Edition. 2 nd ed. Society for Industrial and Applied Mathematics, Apr. 2003. Url: http://www-users.cs.umn.edu/~saad/PS/All_pdf.Zip.
- Jonathan Richard Shewchuk et al. An introduction to the conjugate Gradient method without the agonizing pain. 1994.
- O. Ubbink. “Numerical prediction of two fluid system with sharp Interfaces”. PhD thesis. Imperial College of Science, 1997.
- H. K. Versteeg and W. Malalasekra. An Introduction to Computational Fluid Dynamics: The Finite Volume Method Approach. Prentice Hall, 1996.
- H. G. Weller et al. “A tensorial approach to computational continuum mechanics using object-oriented techniques”. In: Computers In Physics 12.6 (1998), pp. 620–631.
在进入本章的详细内容之前,需要将一些概念放入背景中。在计算流体力学(CFD)的背景下,几何体本质上是流动区域的三维表示。另一方面,网格可以有多重含义,但在这里通常考虑的是三维体积网格。当然,也存在一些小的变化,例如表面网格,它是对表面进行离散化处理。对于表面离散化,与体积网格不同的是使用平面单元而不是体积单元。对于复杂的几何体,正确定义表面网格可能是至关重要的。
从计算流体力学(CFD)的角度来看,与每个特定流动问题相关的几何形状是感兴趣的。以模拟汽车周围流动的空气动力学为例,汽车内部通常并不重要,因为它在整体流动中没有显著贡献。因此,只有汽车外部的细节才是相关的,并且需要在空间离散化中得到充分求解。
本章概述了如何从头开始创建网格,如何在不同格式之间转换网格,以及创建网格后用于操作网格的各种实用程序。
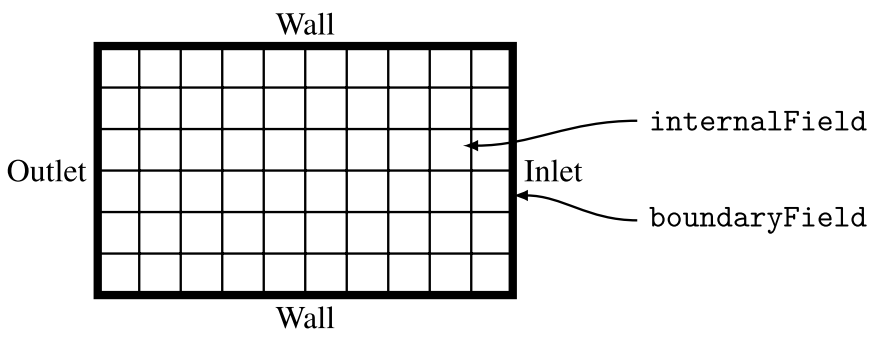
区分实际网格几何图形和由计算辅助设计(CAD)程序生成的几何图形非常重要。虽然在上一章中已经用了一些关于一般网格连接的内容,但这里还是给出了实际网格是如何存储在文件系统中的概述。在标准的OpenFOAM案例中,有三个主要目录:0、constant和system。0文件夹存储网格生成过程中不需要的场的初始条件,system目录存储与模拟的数值和整体执行有关的设置。本章考虑的是constant目录,因为其存储网格,包括所有与空间和连接相关的数据。有关OpenFOAM案例结构的其他详细信息将在第3章中提供。
只要使用静态网格,计算网格始终存储在Constant/PolyMesh目录中。此处的静态网格是指在模拟过程中不会发生改变的网格,即使点位移或连接性发生变化。网格数据自然位于此处,因为假设它是恒定的,因此是Constant文件夹。从编程的角度来看,它被描述为PolyMesh,这是对OpenFOAM网格及其所有功能和限制的一般描述。对于给定的静态网格情况,网格数据将存储在常量/多边形网格中。这里找到的典型网格数据文件包括:points、faces、owner、neighbour及boundary。当然,包含的数据必须有效,才能正确定义网格。
在下面的讨论中,以potentialFoam求解器的PitzDaily教程为例,可以通过发出以下命令找到该示例
?> tut
?> cd basic/potentialFoam/pitzDaily
检查PolyMesh目录的内容后,很明显其还不包含所需的网格数据。本教程中仅提供了blockMeshDict,在case目录中执行blockMesh会生成网格和关联的连接数据:
?> ls constant/polyMesh
blockMeshDict boundary
?> blockMesh
?> ls constant/polyMesh
blockMeshDict boundary faces neighbour owner points
以前使用过CFD代码的用户,特别是使用基于结构化网格的代码的用户,可能会错过每个网格单元的寻址。
OpenFOAM中的非结构化FVM方法不是基于每个单元构建网格,而是基于每个网格面构建网格。以下列表说明了Constant/PolyMesh中每个文件的用途。
1、points
定义向量场中网格的所有节点,其中它们在空间中的位置以米为单位。这些点并非细胞中心,而是网格的角点。要将网格在正x方向上平移1米,必须相应地更改每个节点。不需要为此更改polyMesh子目录中的任何其他结构,节2.4介绍了这一点。
通过使用文本编辑器打开相应的文件,可以更仔细地查看这些点。为了限制输出,忽略标题,只显示前几行:
?> head -25 constant/polyMesh/points | tail -7
25012 // 节点数量
((-0.0206 0 -0.0005) // 点0的坐标
(-0.01901716308 0 -0.0005) // 点1的坐标
(-0.01749756573 0 -0.0005)
(-0.01603868134 0 -0.0005)
(-0.01463808421 0 -0.0005)
该文件包含一个包含25012个点的列表。此列表不需要以任何方式排序。此外,列表中的所有节点都是唯一的,这意味着相同的点坐标不能多次出现。访问和寻址这些点是通过vectorField中的列表位置从0开始执行的。该位置存储为label。
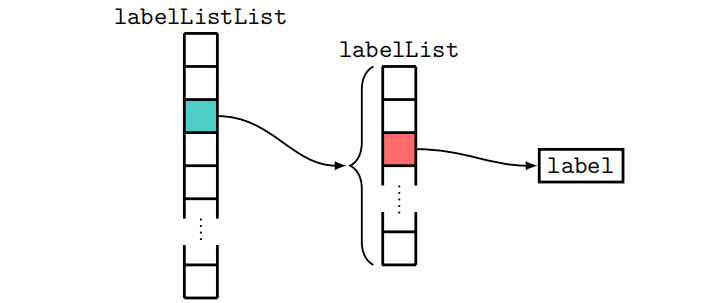
2、faces
根据点在点向量场中的位置合成网格面,并将其存储在labelListList中。这是一个嵌套列表,每个面包含一个元素。这些元素中的每一个都有自己的labelList,存储用于构造面的points的标签。图2.1显示了labelListList的结构。
每个网格面必须至少由三个节点组成,其大小后面紧跟一个点标签列表。在网格面上,每个节点都通过一条直边与其相邻的点相连[4]。使用定义网格面的节点,可以计算表面积矢量,其方向由右手定则确定。
同样,仅显示faces文件的前几行以保持简短:
?> head -25 constant/polyMesh/faces | tail -7
49180 // 网格面的数量
(
4(1 20 172 153) // 网格面0包含4个节点,其标签为(1 20 172 153)
4(19 171 172 20)
4(2 21 173 154)
4(20 172 173 21)
4(3 22 174 155)
...
)
从输出的第一行可以看出,网格由49180个网格面组成,上面只显示了其中的一个子集。与面列表的长度49180类似,每个labelList的长度在列表开始之前声明。因此,此处显示的所有面都是从4个点构建的,这些点由它们在点列表中的位置表示。
3、owner
Owner也是一个与存储面的列表具有相同维度的labelList。由于面已构建并存储在面列表中,因此必须定义它们与体网格的从属关系。根据定义,一个网格面只能在两个相邻的网格之间共享。owner列表存储哪个面属于哪个网格,而这是根据网格标签来决定的。具有较低单元格标签的网格拥有该面,其另一个面被视为neighbor。它指示代码第一个面(列表中的索引0)属于标签存储在该位置的网格。
查看下面的owner文件可知,网格面0、1、2、3分别归属于网格单元0、0、1、1。owner文件中的网格面数量与faces文件中的网格面数量一致。
?> head -25 constant/polyMesh/owner | tail -7
49180
(0
0
1
1
同样,上一章解释了owner-neighbour寻址的工作原理。
4、neighbour
neighbour必须与owner列表结合起来一起考虑,其与owner列表相反。neighbour存储相邻的网格,而不是定义哪个网格拥有每个特定的面。将owner文件与neighbour文件进行比较,可以发现它们的主要区别:owner列表要短得多。这是因为边界面没有相邻的网格。
?> head -25 constant/polyMesh/neighbour | tail -7
24170
(1
18
2
19
5、boundary
边界包含有关嵌套子字典列表中网格边界的所有信息。边界通常被称为patch或边界patch。与之前的网格组件类似,仅显示了一些相关行:
?> head -25 constant/polyMesh/boundary | tail -8
5
(
inlet
{
type patch;
nFaces 30;
startFace 24170;
}
对于本节中使用的 pitzDaily 示例,边界文件包含 5 个patch的列表。每个patch由一个字典表示,由patch名开始。字典中包含的信息包括:patch类型、面数和起始面。由于面列表的排序,可以使用此约定快速轻松地处理属于某个面片的面。
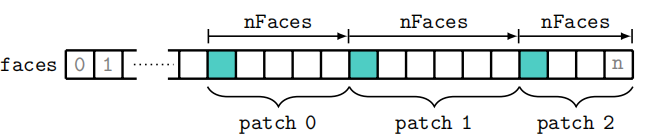
边界面的寻址方法如图 2.2 所示。根据设计,所有没有neighbor的面都被存放在faces列表的末尾,根据他们的owner patch对其进行排序。所有作为边界面的面都必须被边界描述所覆盖。
从用户的角度来看,点和面、owner和neighbor都不需要手动接触或操作。如果手动更改它们,这肯定会破坏网格。但是,根据工作流程,可能需要针对某些设置更改边界文件。更改边界文件的最可能原因是更改patch名称或类型。在此处进行此更改可能比重新运行相应的网格生成器要容易得多。
现在解释了 OpenFOAM 网格的基本结构,接下来将回顾边界类型。有几种类型可以分配给边界,其中一些比其他更常见。区分边界(或patch)和边界条件(见图 2.3)很重要。
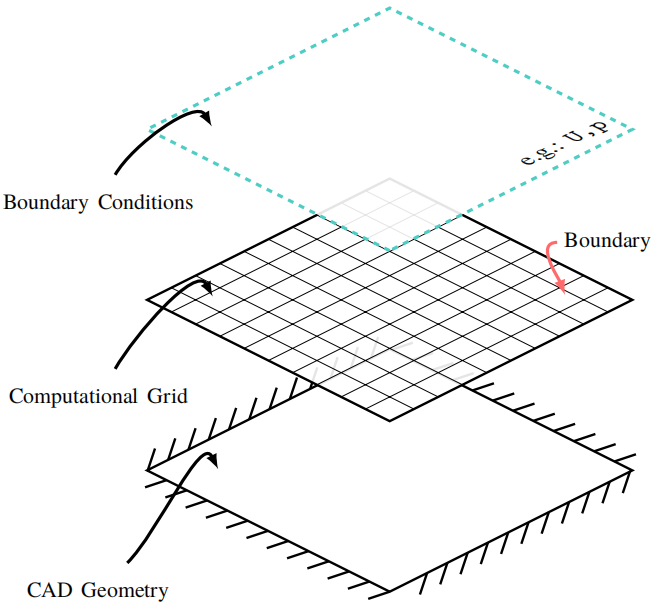
patch是计算域的外边界,其在边界文件中指定,因此是一种拓扑属性。边界和 CAD 几何之间的逻辑联系是两者的表面应尽可能相同。用网格拓扑表示,它是一组面,只有一个owner网格,没有neighbor网格。与patch相反,边界条件分别应用于每个物理场(U、p 等)的patch。patch类型有:
Patch。大多数patch(边界)可以用patch类型来描述,因为它是最一般的描述。 Neumann、Dirichlet 或 Cauchy 边界条件都可以应用于这种类型的边界。wall。如果patch被定义为wall,这并不意味着没有流体通过过该边界。它仅使湍流模型能够正确地将壁面函数应用于该patch(参见第 7 章),仍然需要通过速度边界条件明确定义防止流体通过类型为wall的patch。symmetryPlane。将patch类型设置为 SymmetryPlane 声明它充当对称平面。除了 SymmetryPlane 之外,不能对其应用其他边界条件,并且必须将其应用于所有物理场。empty。在二维模拟的情况下,这种类型应该应用于“平面内”的patch。与 SymmetryPlane 类型类似,这些patch的边界条件也必须为所有物理场设置为empty。不会对这些patch应用其他边界条件。两个empty边界之间的所有网格边必须平行,否则无法进行精确的二维模拟。cyclic。如果一个几何结构由多个相同的部件组成(例如螺旋桨叶片或涡轮叶片),则只需将其中一个组件离散化并将其视为位于相同组件之间。对于四叶片螺旋桨,这意味着只有一个叶片是网格化的(90° 网格),并通过将cyclic边界类型分配给具有切线方向法线的patch。然后这些patch将充当物理耦合。wedge。这种边界类型类似于cyclic边界,只是专门为形成小的(例如≤5°)楔形的循环边界设计的。
从执行和兼容性的角度来看,polyMesh 结构的创建方式并不重要,只要网格数据本身是有效的即可。虽然 OpenFOAM 打包了各种网格生成工具,但只要可以进行有效的转换或输出,就可以使用外部第三方网格生成器。
除了上面提到的 OpenFOAM 网格的基本核心组件之外,还有各种可选的网格结构,它们只能用于特定的应用程序。由于它们是可选的,因此无论案例设置如何,它们都可以存在。 OpenFOAM 应用程序会根据需要读取它们,并在它们丢失时向用户报告。
6、Sets及Zones
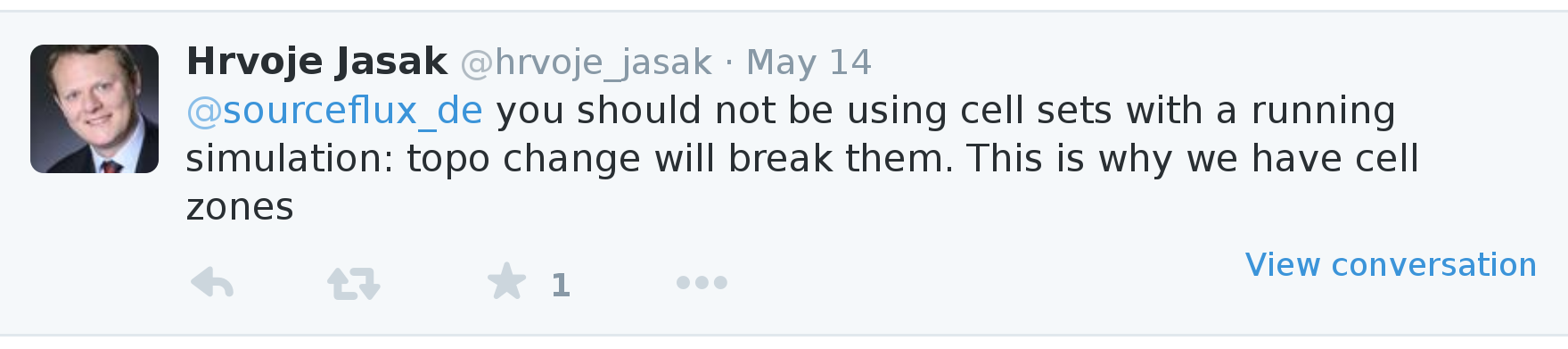
作为用户,当用户担心时,很容易被 OpenFOAM 中的区域(zones)和集合(sets)以及两者都非常相似的事实所混淆:他们选择网格实体。对使用哪个问题的非常简短的回答是:使用区域,正如 Hrvoje Jasak 通过 Twitter 简要解释的那样(参见图 2.4)。
然而,这仅与求解器应用程序真正相关。如果应用程序以预处理或后处理为中心,则任何一个都可以。Set本质上是 labelHashSets,而Zone继承自 labelLists。两者都可以将任何网格实体(点、面或单元)存储在类似于列表的数据结构中。主要区别在于网格实体的内部处理,特别是在具有拓扑网格变化的并行模拟的情况下。在这种情况下,必须相应地更新列表中的地址,并且只有Zone提供这种方法。
选择通常由工具 setSet 或 topoSet 执行,它们都可以选择网格的子集并对其进行布尔运算。一般来说,这两个实用程序都可以将区域转换为集合,反之亦然。可以为任何网格实体(单元、点或面)创建集合或区域,但 cellSet 和 cellZone 是最常用的两个。区域作为普通字典存储在 constant/polyMesh 中,而集合存储在 constant/polyMesh 的 sets 子目录中。区域和集合以相同的方式存储在文件系统中:作为相应网格实体的标签的长列表。
我们已经发布了一些博客文章,其中包含有关区域和集合如何组装的一定程度的信息 [2, 1]。
2.1.1 CAD几何
导入外部 CAD 软件中生成的几何图形是CFD 工程师的常规任务。在 OpenFOAM 中,这通常使用 snappyHexMesh 执行,但是,稍后将解释这个网格生成器的用法。目前唯一重要的概念是本节仅处理Stereolithography(STL) 文件的导入。支持其他文件类型并以类似的方式工作。 STL 是一种文件格式,可以以三角面片方式存储几何图形的表面。二进制和 ASCII 编码文件都是可能的,但为了简单起见,我们将使用 ASCII 编码。
作为 STL 文件的示例,以下代码段显示了仅由一个三角形组成的 STL 曲面:
solid TRIANGLE
facet normal -8.55322e-19 -0.950743 0.30998
outer loop
vertex -0.439394 1.29391e-18 -0.0625
vertex -0.442762 0.00226415 -0.0555556
vertex -0.442762 1.29694e-18 -0.0625
endloop
endfacet
endsolid TRIANGLE
在此示例中,仅定义了一个名为 TRIANGLE 的实体。一个 STL 文件可能包含多个实体,这些实体一个接一个地定义。组成表面的每个三角形都有一个法线向量和三个点。
使用 ASCII STL 文件的缺点是它们的文件大小会随着表面分辨率的增加而迅速增长。边没有明确包含,因为文件中只存储了三角形。因此,从 STL 中识别和提取特征边缘有时是一项具有挑战性的任务。
使用 STL 作为文件格式的一个优点是可以获得三角形表面网格,根据定义,它总是具有平面表面组件(三角形)。
有很多专门为 OpenFOAM 设计的开源网格生成器,分布在两个主要开发分支(vanilla OpenFOAM 和foam-extend)中。这包括 blockMesh、snappyHexMesh、foamyHexMesh、foamyQuadMesh 和 cfMesh。还有一些其他的工具,如extrudeMesh 和 extrude2DMesh,但在本节中没有讨论,因为多数 OpenFOAM 用户不使用它们。此外,它们主要属于网格实用程序,而不是本章讨论的核心网格生成器。本节将简要介绍 blockMesh 和 snappyHexMesh,并回顾它们的用法和工作原理。一般来说,网格生成器的目的是以用户友好的方式生成上一节中描述的 polyMesh 数据结构。两个网格生成器具有相似的输入和输出,因为它们读取字典文件并将最终网格写入constant/polyMesh文件中。
2.2.1 blockMesh
当调用可执行的 blockMesh 时,会自动从 constant/polyMesh 目录中读取blockMeshDict ,因此该目录文件必须存在。
blockMesh 生成块结构的六面体网格,然后将其转换为 OpenFOAM 所需的任意非结构化格式。使用 blockMesh 为复杂的几何图形生成网格通常是一项非常乏味和困难的任务,有时甚至是不可能的。对于复杂的几何图形,用户生成 blockMeshDict 所花费的精力会大大增加。因此,通常只使用 blockMesh 生成简单的网格,然后将实际几何的离散化转移到 snappyHexMesh。这使得 blockMesh 成为生成网格的好工具,这些网格要么由相当简单的几何体组成,要么为 snappyHexMesh 生成背景网格。
blockMesh 用于构建网格的示例块如图 2.5 所示。每个块由称为顶点的 8 个角组成。六面体块是从这些角点及边线构建的。
如图 2.5 所示,将顶点相互连接。最后,块的表面由patch定义,尽管这些patch仅必须为没有相邻块的块边界显式指定。两个块之间的边界不得在patch定义中列出,因为根据定义,它们不是patch。特定边上的节点的长度和数量必须匹配,以保持拓扑一致。实际模拟的边界条件稍后将应用于这些patch。
请注意,可以生成少于 8 个顶点的块并且在patch上具有不匹配的节点(请参阅 [4]),但是,本指南不涵盖这一点。块的边缘默认为直线,但可以替换为不同的线类型,例如圆弧、多段线或样条线。选择例如圆弧确实会影响块边缘拓扑的形状,但该边缘上最终网格点之间的连接保持直线(见图 2.6)。
1、坐标系统
最终网格在全局(右手)坐标系中构建,该坐标系是笛卡尔坐标系并与主要坐标轴对齐:x、y 和 z。当块必须在空间中任意对齐和定位时,这会导致问题。为了避免这个问题,每个块都分配有自己的右手坐标系,根据定义,这并不要求三个轴正交。这三个轴标记为 x1、x2、x3(参见 [4] 和图 2.5)。根据图 2.5 所示的符号定义局部坐标系:顶点 0 定义原点,顶点对 (0, 1) 表示 x1,而 x2 和 x3 由顶点对 (0, 3) 和 (0, 4)分别定义。
2、节点分布
在网格划分过程中,每个块被细分为单元。单元由块坐标系的三个坐标轴中每个坐标轴的边缘上的节点定义,并遵循下式给出的关系: 用户可以在 blockMeshDict 中定义在某条边上将出现多少个单元格。边上的单元可以均匀分布,也可以基于分级分布在非均匀分布上。存在两种类型的分级:simpleGrading 和 edgeGrading based。 simpleGrading 描述了基于特定边缘上最后一个网格与第一个网格的大小比对边缘的分级(见图 2.7):
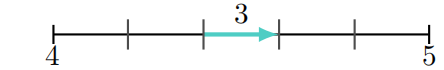
如果 ,所有节点都在该指定边上均匀分布,则不存在分级。当膨胀比 时,节点间距从边的开始到结束增加。从 blockMesh 的 C++ 源代码中可以发现,由用户 (er) 定义的扩展比由以下关系缩放:
其中表示该指定边上的节点数。通第个节点在边上的相对位置可以通过下式计算:
{\lambda(r, i)=\frac{1-r^{i}}{1-r^{n}} \quad \text { with } \lambda \in[0,1]}\tag{2.4}\label{2.4}
尽管对于BlockMeshdict中的所有块来说,这看起来太费力了,但当需要在相邻的两个块之间平滑地转换网格大小时,这就派上了用场。 在许多情况下,简单的试错通常就足够了。
3、为最小示例定义字典
作为如何正确设置BlockMeshdict的一个小例子,对一个体积为1m3的立方体进行了离散化。 可以在示例案例存储库的chapter2/blockMesh目录中找到准备好的案例。字典由一个关键字和四个子字典组成。 第一个关键字是convertTometers,通常为1。 所有的点位置都是按这个因子缩放的,如果几何尺寸很大或很小,这就派上了用场。 在任何这种情况下,我们最终都会键入大量的前导零或后导零,这是一项乏味的任务。 通过相应地设置convertTometers,我们可以节省一些键入。blockmeshdict的第一个相关行是:
convertToMeters 1;
其次,必须定义顶点。 重要的是要记住BlockMesh中的顶点不同于所创建的PolyMesh中的点,尽管它们的定义相当相似。 对于单位立方体示例,顶点定义为
vertices
(
(0 0 0)
(1 0 0)
(1 1 0)
(0 1 0)
(0 0 1)
(1 0 1)
(1 1 1)
(0 1 1)
);
通过查看上面的定义,可以清楚地看出该语法是一个列表,类似于polymesh定义中的点列表。 这是由于在OpenFoam中圆括号指示列表,而花括号则定义字典。 前四行定义了平面中的所有四个顶点,下面的行定义了平面中的所有四个顶点。 与polymesh中的点类似,每个元素都是通过其在列表中的位置而不是坐标来访问的。 请注意,每个顶点必须是唯一的,因此在列表中只出现一次。
下一步,必须定义这些块。 图2.5可以作为参考。 单位多维数据集的示例块定义如下所示:
blocks
(
hex (0 1 2 3 4 5 6 7) (10 10 10) simpleGrading (1 1 1);
);
同样,由于圆括号的存在,这是一个包含块的列表,而不是字典。 这个定义乍一看可能有点奇怪,但实际上很直截了当。 第一个单词hex和第一组包含八个数字的圆括号告诉blockMesh在顶点0到7中生成一个六面体。 这些顶点正是上面顶点部分中指定的顶点,并通过它们的标签进行访问。 它们的顺序不是任意的,而是由如下所示的局部块坐标系定义的:
- 对于局部平面,列出所有从原点开始并按照右手坐标系移动的四个顶点标记。
- 对局部平面执行相同操作
通过打乱特定块定义中顶点列表的顺序可以获得有效的块定义。 生成的块将看起来扭曲或使用不正确的全局坐标方向。 一旦执行blockMesh和checkMesh并在后处理器(例如Paraview)中分析网格,就检测到这一点。
注:checkMesh是一种原生的OpenFOAM工具,用于根据各种标准检查网格的完整性和质量。如果checkMesh的输出指出网格不正常,则必须对其进行改进。
第二组圆形括号定义了在块的每个特定方向上分布多少单元格。 在这个示例中,块每个方向有10个网格格。 若修改方向为2个网格,中为20个网格,中为1337个单元格,则块定义可以写为:
hex (0 1 2 3 4 5 6 7) (2 20 1337) simpleGrading (1 1 1);
最后剩下的是SimpleGrading部分,与圆括号中的最后一组数字结合在一起。 如前所述,这是定义分级(或扩展比率)的最简单的方法。 在本例中,关键字simpleGrading定义了三个局部坐标系轴方向上所有四条边的等级分为相同。 因此simpleGrading后面括号中的三个数字分别定义了、和方向的分级。 不过,有时这还不够通用。 这就是可以使用edgeGrading的地方。 这种更先进的分级方法本质上与simpleGrading相同,但可以明确指定六面体上12条边中每条边的分级,此时最后一组括号不会列出3个数字,而是3乘以4。 现在,每个边都可以单独设置。
保存blockMeshdict文件并在之后执行blockMesh,将得到一个与blockMeshdict中定义的类似的有效网格。 但是blockMesh会警告未定义的patches,这些patch默认被放入DefaultFaces中。
手动指定patch是通过在名为patches的列表中定义它们来完成的,对于示例patch 0:
patches
(
XMIN
{
type patch;
faces
(
(4 7 3 0)
);
}
);
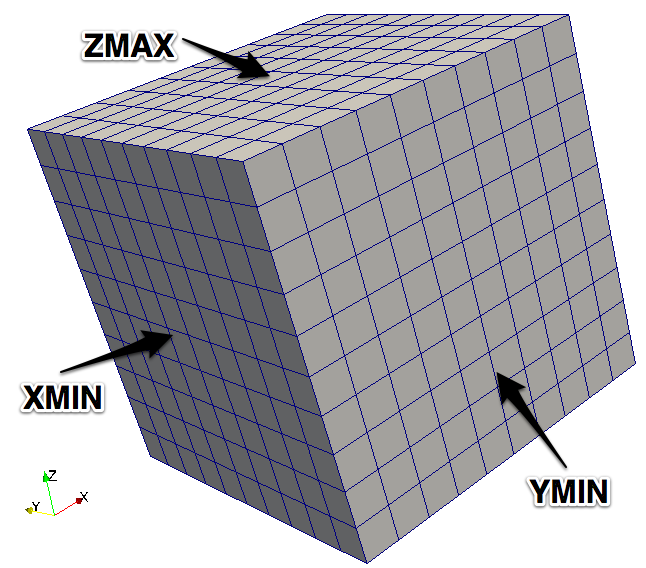
这将指示blockMesh根据从顶点4、7、3和0构造的面生成名为Xmin的patch类型的patch。在内部,patch名称定义为word,并且此数据类型会定期显示在错误消息中。不过,顶点的排序方式不是任意的。它们需要从块内部看以顺时针方向指定。图2.8显示了示例的单位立方体的图像,该立方体由1000个小立方体组成,带有突出显示的XMIN,YMIN和ZMAX的patch。用于生成此网格的文件可以在chapter2/blockMesh下的示例存储库中找到。
如前所述,缺省情况下,块的边是行,因此包含边定义的列表是可选的。 与上面定义的块和patch非常类似,通过弧线而不是默认线连接两个顶点将如下所示:
edges
(
arc 0 1 (0.5 -0.5 0)
);
包含边定义的列表中的每个项都以指示边类型的关键字开始,然后是开始和结束顶点的标签。 在本例中,这条线被构造弧所需的第三个点闭合。 对于任何其他边形状(例如折线或样条),该点将被一系列支撑点所取代。
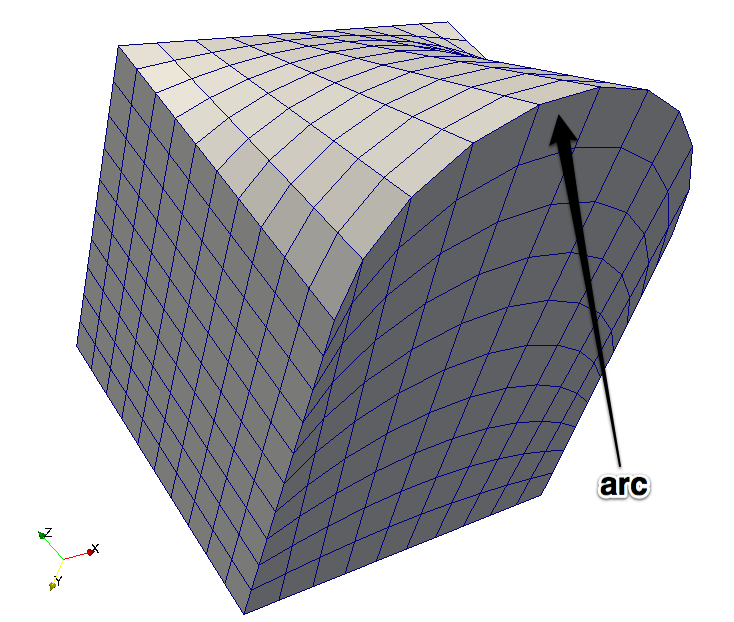
插入上面列出的代码如何改变单位立方体的形状(参见图2.8),在图2.9中给出了一个示例。
要继续SnappyHexMesh部分,需要生成一个由每个方向的50个单元格组成的单位立方体。
2.2.2 snappyHexMesh
与BlockMesh相比,snappyHexMesh可能不需要太多繁琐的工作,比如添加和连接块。 另一方面,对最终网格的控制较少。 使用snappyHexMesh,可以轻松生成六面体占优网格,只需要两件事:一个六面体背景网格,第二个是一个或多个兼容曲面格式的几何图形。 snappyHexMesh支持由各种体积形状定义的局部网格细化(见表2.1),边界层单元(棱镜和多面体)的应用以及并行执行。
snappyHexmesh是一个复杂的程序,由大量的控制参数控制。 详细描述这些超出了本书的范围。 请结合本书阅读[4],以获得对snappyHexMesh更深入的讨论。 其他信息可以在这里[5]找到。
snappyHexMesh的执行流程可以分为三个主要步骤,然后依次执行。可以通过在snappyHexMeshDict的开头将相应的关键字设置为false来禁用这些步骤中的每个步骤。这三个步骤可以概括如下:
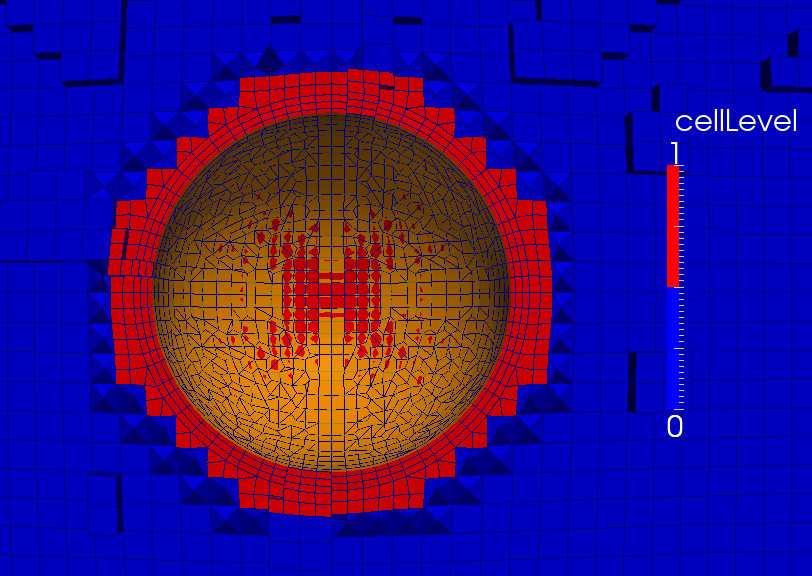
castellateMesh。这是第一阶段,执行两个主要操作。首先,它将几何形状添加到网格中,并删除不在流动域内的单元。其次,根据用户的指定对现有单元格进行拆分和细化。结果是一个仅由或多或少类似于几何形状的六面体组成的网格。但是,应该放置在几何图形表面上的大多数网格点都不与它对齐。在图2.10中示出了在网格划分过程的这一阶段的后面示例的屏幕截图。snap。通过执行捕捉步骤,表面附近的网格点被移动到表面上。 这一点在图2.11中可见一斑。 在此过程中,这些网格的拓扑结构可能由六面体变为多面体。 靠近表面的网格可能被删除或合并在一起。

addLayers。最后,在几何表面上引入额外的单元,通常用于细化近壁流动(见图2.12)。 将预先存在的单元从几何图形中移开,以便为额外的单元创造空间。 那些网格很可能是棱柱层。
上述所有设置以及更多设置都在system/snappyHexMeshDict中定义,该字典包含snappyHexMesh所需的所有参数。在网格化/snappyHexMesh下的OpenFOAM教程目录中可以找到一些有用的教程。与其他OpenFOAM字典相比,snappyHexMeshDict非常长,由许多层次结构级别组成,这些层次结构级别由嵌套的子词典表示。对于上述每个步骤 (假设您具有标准配置),将一个时间步骤写入case目录。这三个步骤中的每一个将在下一节中单独讨论。
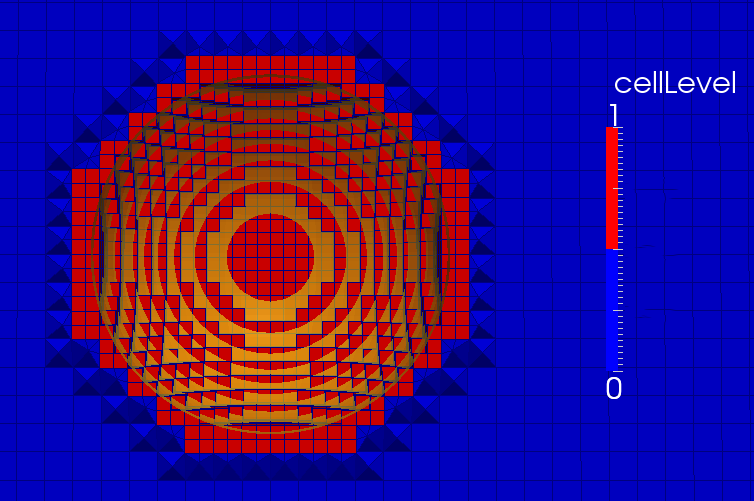
2.2.2.1 Cell levels
网格级别用于描述背景网格单元格的细化状态。 启动snappyHexMesh时,将读取背景网格,并将所有单元格分配为单元格级别0(图2.12中为蓝色单元格)。
如果一个网格被细化一个级别,每个边缘被减半,从前一个“父”单元格生成八个单元格。 这种细化方法基于八叉树,只适用于六面体,这就是为什么snappyHexmesh需要六面体背景网格。 使用snappyHexmesh不可能只在一个方向上细化单元格,因为八叉树无法覆盖这一点。 因此根据定义,它们在所有三个空间方向上都是一致的。
2.2.2.2 定义几何图形
在snappyHexMeshdict中定义任何内容,constant/polymesh中的现有网格将自动读取并用作背景网格。 如果没有这样的网格可用,或者如果它不是纯粹基于六面体,snappyHexmesh将无法运行。 对于外部流动模拟,由背景网格定义的外部边界不如内部流动重要。 因此,它们可以保持由背景网格定义,而不需要在它们上花费更多的工作。 另一方面,在内部流动模拟中,背景网格的外部形状是由实际几何形状定义的,因此它是不受关注的。
STL几何图形可以使用几乎任何CAD程序生成。 Paraview可用于生成基本形状的STL表示,如圆柱、球体或锥体。 在sources菜单下,可以使用file菜单下的save data项导出各种形状。
对于现实世界的几何学,当然有各种方法来生成曲面网格并将其存储为STL。 然而,请记住,表面网格的质量对获得良好的体积网格至关重要。
作为一个简单的例子,在前一节中准备的单位立方体网格被重用,并在其中插入一个球体。 球体是使用STL文件生成的,而不是表2.1中列出的形状。 加载STL几何图形可以以直接的方式完成,只需将几何图形复制到case的constant/triSurface,并在snappyHexMeshdict中添加以下几何图形子字典。 一个这样的示例如下所示:
geometry
{
sphere.stl // Name of the STL file
{
type triSurfaceMesh; // Type that deals with STL import
name SPHERE; // Name access the geometry from now on
}
}
上面的行告诉snappyHexMesh从constant/triSurface中读取spher.stl作为triSurfaceMesh,并将该STL中包含的几何体引用为sphere。一些简单的几何对象可以在不需要打开任何CAD程序的情况下直接在snappyHexMesh中构建。表2.1列出了这些几何形状。
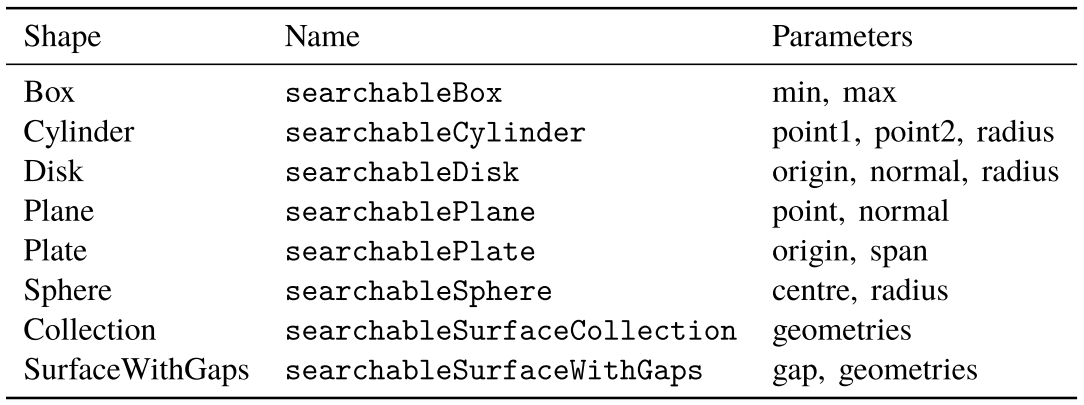
表2.1中列出的任何形状都可以在geometry子字典中构造,方法是简单地追加到现有的子字典中。例如,要将一个box添加到几何子字典中,该子字典由最小点和最大点构成。使用此方法时,不可能直接旋转长方体,它将始终与坐标轴对齐。
smallerBox
{
type searchableBox;
min (0.2 0.2 0.2);
max (0.8 0.8 0.8);
}
与STL定义类似,定义searchableBox的子字典的前导字符串是用于稍后访问该几何体的名称。有时候,我们希望用表2-1中列出的形状组合一个几何体,但要将其视为一个几何体而不是多个几何体。这是可以使用searchableSurfaceCollection的地方。通过在已经存在的几何体组件上使用此方法,可以组合、旋转、平移和缩放曲面。在任何情况下,将SPHERE和smallerBox合并为一个,并将fancybox放大2倍,将如下所示:
geometry
{
...
fancyBox
{
type searchableSurfaceCollection;
mergeSubRegions true;
SPHERE2
{
surface SPHERE
scale (1 1 1);
}
smallerBox2
{
surface smallerBox;
scale (2 2 2);
}
}
}
2.2.2.3 设置castellatedMesh步骤
这是执行snappyHexMesh期间三个步骤中的第一个步骤。它包括以下两个主要步骤:根据用户规范分割单元并删除网格区域之外的单元。图2.13给出了这一过程的示意图。
现有的背景网格(图2.13中的黑色)从constant/polyMesh中读取。根据snappyHexMeshDict的castellatedMeshControls子字典中的参数细化网格。区分由几何曲面定义的细化和体积细化是很重要的。曲面细分可确保表示几何图形的边界面细分到定义的层级。需要注意的是,这不仅会影响拥有特定单元的单元,还会影响邻近的单元。因此,表面细化可能看起来有点类似于体积细化,但是,它是明显不同的。对SPHERE应用这样的曲面细化由castellatedMeshControls中的条目控制,如下所示:
castellatedMeshControls
{
...
refinementSurfaces
{
SPHERE // Name of the surface
{
level (1 1); // Min and max refinement level
}
}
...
}
这会将球体的表面细化到1级。圆括号之间的两个数字定义了此曲面的最小和最大细化级别。snappyHexMesh根据曲面曲率在两者之间进行选择:高度弯曲的表面区域被细化到较高水平,较小弯曲的表面区域被细化到较低水平。
snappyHexMesh中的细化不限于曲面定义。在几何子字典中定义的任何几何也可以用作体积细化的定义形状。这些体积细化称为refinementRegions,并在castellatedMesh控件中的同名子字典中定义。与refinementSurfaces相比,refinementRegions提供了更高级别的多功能性,因此需要定义更多选项。
模式有三种选择:inside、outside和distance。 顾名思义,inside只影响选定几何体内的单元格,而outside则恰恰相反。 第三个选项,距离,是两者的组合,并在表面的向外和向内法线方向上计算。 除了modes,还有一个levels选项,它比refinementSurface更复杂。 从名称上已经可以猜到,它确实支持任意数量的级别。 每个级别必须结合distance来定义。 随着在列表中位置的增加,级别必须减少,distance必须增加。 将smallerBox中的任何内容细化到级别1可以通过向castellatedMeshControls添加以下行来完成:
castellatedMeshControls
{
...
refinementRegions
{
smallerBox // Geometry name
{
mode inside; // inside, outside, distance
levels ((1E15 1)); // distance and level
}
}
...
}
上述代码使用 m的距离,以便安全地选择几何体内部的所有网格单元。
如果不指定位于最终网格体积内的点,snappyHexMesh就无法确定用户要离散化球体的哪一侧。这就是为什么locationInMesh关键字也必须在castellatedMeshControls子字典中定义的原因。此点不得放置在背景网格的面上。对于单位立方体示例,该点定义为:
locationInMesh (0.987654 0.987654 0.987654);
下一步是调整snappyHexMeshDict中snap子字典的参数。
2.2.2.4 设置捕捉步骤
与snappyHexMesh的其他两个步骤相比,这不需要大量的用户输入。此步骤负责通过将新点引入网格并替换它们来将纯六面体网格面与几何体对齐(请参见图2.11)。这是一个高度迭代的过程,这就是为什么不需要太多用户交互的原因。snappyHexMeshDict的示例snapControls子字典如下:
snapControls
{
nSmoothPatch 3;
tolerance 2.0;
nSolveIter 30;
nRelaxIter 5;
// Feature snapping
nFeatureSnapIter 10;
implicitFeatureSnap false;
explicitFeatureSnap true;
multiRegionFeatureSnap false;
}
只定义了迭代计数器、容差和标志。 一半的参数处理到几何体边缘的对齐,这不是本描述的一部分。 然而,对此的描述可以在[3]中找到。 根据具体情况,增加迭代计数器通常会得到更高质量的网格,但也会显著增加网格划分时间。
所有参数在OpenFOAM提供的snappyHexMeshDicts中有更详细的解释。
2.2.2.5 设置addLayers步骤
addLayers步骤的所有设置都在snappyHexMeshDict的addLayersControls子字典中定义。可以使用任何表面从挤出棱柱层,而不论其类型为何。首先,需要通过layers子字典指定每个边界要拉伸的单元层数。示例条目如下所示:
addLayersControls
{
...
layers
{
"SPHERE_.*" // Patch name with regular expressions
{
nSurfaceLayers 3; // Number of cell layers
}
}
...
}
每个patch名称后跟一个包含nSurfaceLayers关键字的子字典。此关键字定义要拉伸的网格层数,因此后面跟一个整数,表示要拉伸的网格层数。在上面的示例中,使用正则表达式来匹配以SPHERE_开头的任何patch程序名称。在这种情况下,它只是球体本身,但是以这种方式使用通配符可以大大减少设置时间。最终网格的横截面如图2.12所示。
snappyHexMesh的各种参数(尤其是与层挤出相关的参数)需要进行调整,以获得符合要求的网格。下面简要解释其中的几个。
- relativeSizes可以针对以下值从绝对标注切换到相对标注。默认情况下为true。
- expansionRatio定义从一个网格层到下一个网格层的扩展因子。
- finalLayerThickness是最后一个网格层(距离壁面最远)相对于网格的下一个网格的厚度,或以绝对米为单位,具体取决于对relativeSizes参数的选择。
- minThickness如果层的厚度不能大于minThickness,则不会拉伸该层。
在该示例中,采用了以下所示的设置。
relativeSizes true;
expansionRatio 1.0;
finalLayerThickness 0.5;
minThickness 0.25;
最后,必须在case目录中执行snappyHexMesh以开始网格化过程。每个步骤都会生成一个新的时间点目录,其中包含该特定阶段的网格。如果选择通过调整snappyHexMeshDict中的参数来更改网格,请记住在重新运行snappyHexMesh之前删除旧的时间点。
- 另一个用于OpenFOAM的高质量网格生成器是enGrid,可以从www.example.com免费获得http://engits.eu/en/engrid。
- cfMesh应用程序是一个分布式内存并行OpenFOAM网格工具,它与snappyHexMesh一样,将STL曲面作为输入。此软件包由Creative Fields Ltd.开发,可在www.c-fields.com上与文档一起下载。
2.2.3 cfMesh
cfMesh库是一个跨平台库,用于自动生成网格,它构建在OpenFOAM之上。它与OpenFOAM和foam-extend的所有最新版本兼容,并根据通用公共许可证(GPL)授权。该库由Franjo Juretić博士开发,并由Creative Fields Ltd.发布,可从http://www.c-fields.com 下载。
本节简要概述了库、控制网格生成过程的选项以及cfMesh附带的一些实用程序。它绝不是项目的完整文档。有关更多信息,请访问上述项目网页。
cfMesh库支持使用主库中的组件构建的各种3D和2D工作流,这些组件是可扩展的,可以组合到各种网格化工作流中。核心库基于网格修改器的概念,可通过消息传递接口(MPI)使用对称多处理器(SMP)与分布式内存并行(DMP)实现高效的并行化。此外,还特别注意内存使用,通过实现数据容器(列表、图形等)来保持较低的内存使用。其在网格化处理期间不需要许多动态存储器分配操作。
cfMesh中的网格化过程是自动进行的,需要输入三角剖分和包含各种网格化参数(设置)的字典。给定曲面网格和设置后,网格化过程将从控制台启动,并且自动运行,无需任何用户干预。该库经过优化,网格化工作流需要的设置较少,并且语法简单。目前,cfMesh可以在内部创建体积网格,请参见图2.14,它不需要几何封闭。

2.2.3.1 可用网格化工作流
所有工作流都针对共享内存计算机进行并行化处理,并在运行时使用所有可用的CPU内核。使用的核心数可由OMP_NUM_THREADS环境变量控制,该变量可设置为所需的核心数。
可用的网格划分工作流通过从输入几何图形和用户指定的设置创建所谓的网格模板来启动网格划分过程。 模板随后被调整以匹配输入几何图形。 将模板拟合到输入几何形状的过程被设计为能够容忍质量差的输入数据,这不需要封闭几何。 可用的工作流因模板中生成的网格类型而不同。
笛卡尔工作流生成的三维网格主要由六面体单元组成,不同尺寸单元之间的过渡区域为多面体。 它是通过在shell窗口中键入CartesianMesh开始的。 默认情况下,它生成一个边界层,可以根据用户的要求进一步细化。 此外,该工作流可以使用MPI并行化来运行,该并行化用于生成不适合于单个可用计算机内存的大型网格。
该工作流将生成2D笛卡尔网格。在控制台中键入cartesian 2DMesh可启动网格生成器。依预设,它会产生一个边界层,可进一步细分。此网格化工作流需要带状几何体,如图2.16a所示,该几何体在x-y平面中延伸并在z方向上拉伸。

四面体工作流生成由四面体单元组成的网格,如图2.17所示,并通过在控制台中键入tetMesh启动。默认情况下,它不生成任何边界图层,并且可以根据用户请求添加和优化边界层。
2.2.3.2 输入几何
cfMesh使用的几何尺寸需要以曲面三角剖分的形式定义。对于2D情况,几何图形以三角形带的形式给出,其边界边位于x-y平面中(不支持其他方向)。几何由下列对象组成:
- List of points。包含曲面三角剖分中的所有点。
- List of triangles。包含曲面网格中的所有三角形。
- Patches。在网格划分过程中转移到体网格上的实体。 曲面中的每一个三角形都分配给单个的patch,不能分配给多个patch。 每个patch由其名称和类型标识。 默认情况下,所有patch名称和类型都被转移到体积网格中,并且很容易用于定义模拟的边界条件。
- Facet subsets。在网格划分过程中没有转移到体网格上的实体。 它们用于定义网格划分设置。 每个面子集包含曲面网格中三角形的索引。 请注意,曲面网格中的三角形可以包含在多个子集中。 刻面子集可以由cfSuite生成,cfSuite是由Creative物理场有限公司开发的商业应用程序。
- Feature edges。特征边在网格化过程中被视为约束。三条或更多特征边相交的曲面点被视为角点。特征边可以通过surfaceFeatureEdges工具或cfSuite生成。
图2.18显示了一个带有高亮显示的patch的曲面网格。
由cfMesh转换的所有尖锐特征必须在网格化过程之前由用户定义。在网格划分过程中,两个面片之间的边界边缘(图2.19a)和特征边缘作为尖锐特征进行处理(见图2.19b)。三角剖分中的其他边不受约束。
网格的文件格式建议:fms、ftr和stl。此外几何可以在所有支持的格式导入带有OpenFOAM surfaceConvert效用。然而这三个建议格式支持定义的patch转移到默认体网格。其他格式还可以用于网格划分但是他们不支持定义输入几何和patch的面上产生的体积网格边界的结束在一个patch。
cfMesh的首选格式为fms,用于保存设置网格作业的所有相关信息。它将补片、子集和特征边存储在单个文件中。此外,它是唯一一种可以将所有几何实体存储到单个文件中的格式,强烈建议用户使用它。
2.2.3.3 字典和可用的设置
网格划分过程由位于案例的系统目录中的meshDict字典中提供的设置来指导。 对于使用MPI的并行网格划分,需要一个位于case的系统目录中的decomposePardict,并且用于并行运行的节点数必须与decomposepardict中的numberofsubdomains条目匹配。 decomposePardict中的其他条目不是必需的。 生成的卷网格写在constant/polyMesh目录中。 meshDict中可用的设置将在本节的其余部分中更详细地解释。
cfMesh库只需要两个强制设置就可以启动网格划分过程:
- surfaceFile。指向几何文件。 几何文件的路径相对于case目录的路径。
- maxCellSize。表示用于网格划分的默认网格大小。 它是域中生成的最大单元格大小。
2.2.3.4 细化设置
当统一的单元大小不令人满意时,cfMesh中有许多用于局部细化源的选项。
- boundaryCellSize选项用于优化边界处的单元格。这是一个全局选项,所请求的网格大小将应用于边界的所有位置。
- minCellSize是一个全局选项,可激活网格模板的自动细化。此选项在像元大于估计要素大小的区域中执行优化。此设置提供的标量值指定此过程可生成的最小像元大小。此选项对于快速模拟非常有用,因为它可以在复杂几何图形中生成网格,用户只需很少的工作。但是,如果需要高网格质量,它会在需要进行网格细化的位置提供提示。
- localRefinement允许在边界处进行局部细化区域。它是一个字典的字典,并且localRefinement主字典中的每个字典都由用于细化的几何图形中的面片或面子集命名。实体的请求像元大小由cellSize关键字和标量值控制,或通过指定additionalRefinementLevels关键字和相对于maxCellSize的所需细化数来控制。
- objectRefinement用于指定体积块内的细化区域。可用于优化的支持对象包括:直线、球体、长方体和截锥。它被指定为字典的字典,其中objectRefinement字典中的每个字典都表示用于细化的对象的名称。
cfMesh中实现的网格化工作流基于由内向外网格化,网格化过程从基于用户指定的单元尺寸生成所谓的网格模板开始。但是,如果网格尺寸局部大于几何要素尺寸,则可能导致该几何形状由网格填充。相反,如果指定的网格大小大于局部特征大小,则几何体中较薄部分的网格可能会丢失。
keepCellsIntersectingBoundary选项是一个全局选项,可确保模板中与边界相交的所有单元仍是模板的一部分。默认情况下,所有网格化工作流仅保留模板中完全位于几何体内部的单元。keepCellsIntersectingBoundary关键字后面必须跟1(活动)或0(非活动)。激活此选项可能会导致局部连接的网格超过间隙,该问题可以通过checkForGluedMesh选项解决,该选项后面还必须跟有1(活动)或0(非活动)。
keepCellsIntersectingPatches选项是在用户指定的区域中保留模板中的单元的选项。它是字典的字典,主字典中的每个字典都以patch或面子集命名。启用keepCellsIntersectingBoundary选项时,此选项处于非活动状态。
removeCellsIntersectingPatches选项是从模板中删除用户指定区域中的单元格的选项。 它是一个字典的字典,主字典中的每个字典都由一个patch或一个方面子集命名。 当KeepCellsIntersectingBoundary选项打开时,该选项处于活动状态。

cfMesh中的边界层从体积网格的边界面向内部拉伸,在网格划分过程之前不能拉伸。 此外,它们的厚度由边界处指定的单元尺寸控制,网格生成器倾向于生成与单元尺寸相似厚度的层。 CFMesh中的层可以跨越多个补丁,如果它们共享凹边或角,且价大于3。 此外,CFMESH从不对边界层的拓扑进行Breask,其最终几何形状依赖于光滑过程。 所有边界层设置都在BoundaryLayers字典中提供。 选项有:
- nlayers指定将在网格中生成的层数。 它不是强制性的。 如果没有指定,网格划分工作流将生成默认的层数,该层数要么为一,要么为零。
- thicknessRatio是连续两层厚度之间的比值。 它不是强制性的。 该比率必须大于或等于1。
- maxFirstLayerThickness确保第一边界层的厚度永远不会超过指定值。 它不是强制性的。
- patchBoundaryLayers设置是一个字典,用于指定单个斑块边界层的局部属性。
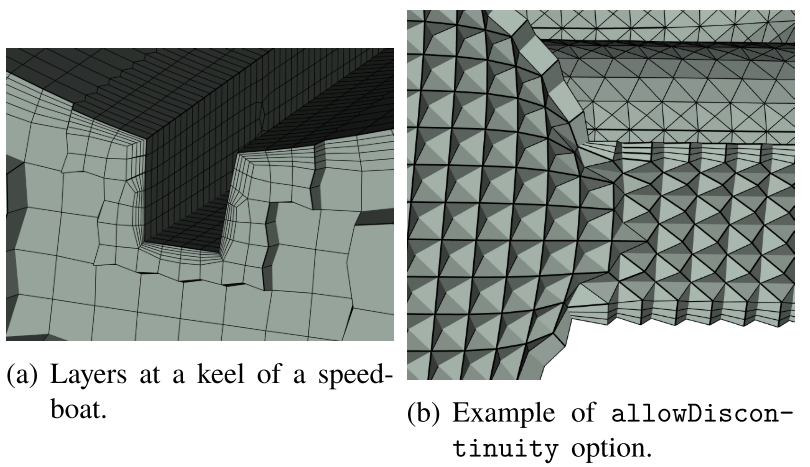
可以在名称与patch名称相同的字典中分别为每个面片指定nLayers,thicknessRatio与maxFirstLayerThickness选项。默认情况下,在面片处生成的层数由全局层数控制,或由在与现有面片一起形成连续层的任何面片处指定的最大层数控制。allowDiscontinuity选项可确保patch所需的层数不会扩展到同一层中的其他patch。
本节中提供的设置用于在网格生成过程中更改patch名称和类型。这些设置在renameBoundary字典中提供,其中包含以下选项:
- newPatchNames是renameBoundary字典内的字典。它包含带有应重命名的patch名称的词典。对于每个patch,可以使用以下设置指定新名称或新patch类型:
- newName关键字后跟给定patch的新名称。该设置不是必需的。
- type关键字后跟给定patch的新类型。该设置不是必需的。
- defaultName是除newPatchNames字典中指定的patch之外的所有patch的新名称。该设置不是必需的。
- defaultType为所有patch(newPatchNames目录中指定的patch除外)设置新类型。该设置不是必需的。
2.2.3.5 cfMesh中的各种实用程序
目前,cfMesh项目提供了以下实用程序:
- FLMAToSurface将几何体从AVL的flma格式转换为cfMesh可读的格式。输入文件中定义的单元选择将作为面子集进行传输。
- FPMAToMesh是用于从AVL的fpma格式导入体积网格的实用程序。在输入网格上定义的选择将作为子集传递。
- copySurfaceParts将指定多面子集中的曲面多面复制到新曲面网格中。
- extrudeEdgesInto2DSurface将几何图形中作为特征边写入的边拉伸到生成2D网格所需的三角形带中。生成的三角形存储在单个面片中。
- meshToFPMA将网格转换为AVL的fpma格式。
- patchesToSubsets将几何中的曲面片转换为多面子集。
- preparePar创建MPI并行化所需的处理器目录。处理器目录的数目取决于在decomposeParDict中指定的numberOfSubdmains。
- removeSurfaceFacets是用于从曲面网格中移除镶嵌面的工具。应移除的面由面片名称或面子集给出。
- subsetToPatch在曲面网格中创建由给定小平面子集中的小平面组成的patch。
- SurfaceFeatureEdges用于生成几何中的特征边。 如果输出是FMS文件,则生成的边缘存储为特征边缘。 否则,它将生成以所选特征边缘为界的patch。
- SurfaceGenerateBoundingBox在几何图形周围生成一个box。 它不会解决自交集,以防盒子与几何的其余部分相交。
虽然blockMesh和snappyHexMesh是强大的网格生成工具,但用户可能经常使用第三方网格划分工具来定义和离散更复杂的流域。
2.3.1 从第三方网格软件包转换
许多高级外部网格化实用程序在网格生成过程中为用户提供了额外的控制级别。这包括可选元素类型、拟合边界层网格和长度比例控制等。某些网格生成器可以直接导出为功能OpenFOAM网格格式。下面列出了OpenFOAM-3.0中支持转换的网格格式的汇编:
- Ansys
- CFX
- Fluent
- GMSH
- Gambit
- Ideas
- Kiva
- Netgen
- Plot3D
- Star-CD
- tetgen
- KIVA
导入实用程序的功能以及它们使用的命名法差别很大。Fluent导入工具将内部边界转换为faceSet,而其他工具完全忽略此类特征。
由于许可证问题,用于从Star CCM+导入网格的网格转换工具及其相关库需要手动下载和编译,而不是通过Allrun脚本。
如果您的特定网格化软件未在上述列表中提及,则它很可能能够将网格导出为支持的中间格式。
上面提到的所有转换实用程序的源代码可以在这里找到:FOAM_TUTORIALS/incompressible/icoFoam/elbow/ meshConversionTest ?> cd meshConversionTest
转换网格非常简单,只需运行转换实用程序并将网格文件作为参数传递,该参数必须存在于目录中。 在转换过程中,Utility将向控制台输出补丁名称和网格统计信息。 Polymesh目录中包含的文件将相应更新。
```bash
?> fluentMeshToFoam elbow.msh
重要的是要记住,导入的网格只和导出的网格一样好。 对于Fluent网格,由于OpenFoam只支持三维网格,所以不可能导入2D网格。 导入完成后,需要更新case,以反映初始和边界条件文件中的新修补程序名称。 所有现有的补丁可以从导入工具的输出中收集,也可以通过编辑器打开constant/polymesh/boundary手动查找。 对于本教程,U和P物理场是为这个特定的网格预先配置的。
在导入过程中缩放网格就像在命令中添加选项和缩放因子一样简单。 为了本教程,网格应该缩小一个数量级。
?> fluentMeshToFoam -scale 0.1 elbow.msh
在许多第三方网格划分工具中构造网格时,用户通常可以为每个特定的贴片分配边界条件类型,如入口、出口、壁面等。 转换过程将尝试将某些边界条件格式匹配到相应的OpenFoam格式,但不能保证边界条件转换的成功或准确性。 检查转换是否正确解析了流信息是至关重要的。 要检查这一点,请检查constant/polymesh/boundary,并在新转换的网格上运行checkmesh。
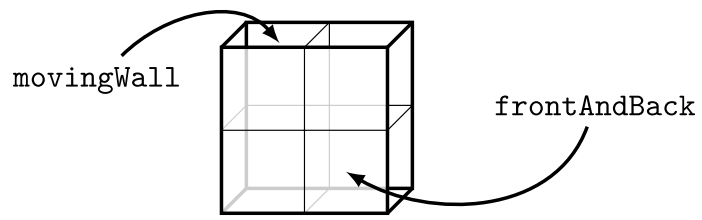
2.3.2 从二维网格到轴对称网格的转换
为了将网格转换为轴对称网格,必须满足以下要求。 网格必须已经是一个有效的OpenFOAM网格,它必须只有一个网格“厚”。 后一个要求对OpenFOAM中的所有二维网格都有效。 由于icoFoam的腔体示例满足所有这些要求,因此本教程使用它。 它位于$foam_tutorials/incompressible/icofoam/cavity。
由于网格形状为矩形并且只有一个单元,因此可以创建非常基本的几何体。在OpenFOAM中,轴对称网格具有以下属性:网格为一个单元“厚”,并绕对称轴旋转以形成5°楔形。楔形体的两个成角度边界被视为楔形体类型的单独patch。
makeAxialMesh的来源可在OpenFOAM wiki上找到:http://openfoamwiki.net/index.php/Contrib_MakeAxialMesh。按照其中的说明下载并编译该实用程序。
接下来的步骤是在您选择的工作目录中创建案例文件夹的副本,重命名该目录以避免将来发生任何混淆,然后创建2D基础网格。
?> cp -r <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.02778em;">FO</span><span class="mord mathnormal">A</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3283em;"><span style="top:-2.55em;margin-left:-0.109em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right:0.13889em;">T</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord mathnormal" style="margin-right:0.10903em;">U</span><span class="mord mathnormal" style="margin-right:0.00773em;">TOR</span><span class="mord mathnormal" style="margin-right:0.07847em;">I</span><span class="mord mathnormal">A</span><span class="mord mathnormal">L</span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord">/</span><span class="mord mathnormal">u</span><span class="mord mathnormal">t</span><span class="mord mathnormal">i</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">i</span><span class="mord mathnormal">t</span><span class="mord mathnormal">i</span><span class="mord mathnormal">es</span><span class="mord">/</span><span class="mord mathnormal">in</span><span class="mord mathnormal">co</span><span class="mord mathnormal">m</span><span class="mord mathnormal">p</span><span class="mord mathnormal">ress</span><span class="mord mathnormal">ib</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">e</span><span class="mord">/</span><span class="mord mathnormal">i</span><span class="mord mathnormal">co</span><span class="mord mathnormal" style="margin-right:0.13889em;">F</span><span class="mord mathnormal">o</span><span class="mord mathnormal">am</span><span class="mord">/</span><span class="mord mathnormal">c</span><span class="mord mathnormal">a</span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mord mathnormal">i</span><span class="mord mathnormal">t</span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span><span class="mord">.</span><span class="mclose">?</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">></span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord mathnormal">m</span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mord mathnormal">c</span><span class="mord mathnormal">a</span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mord mathnormal">i</span><span class="mord mathnormal">t</span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span><span class="mord mathnormal">a</span><span class="mord mathnormal">x</span><span class="mord mathnormal">i</span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span><span class="mord mathnormal">m</span><span class="mord mathnormal" style="margin-right:0.07153em;">C</span><span class="mord mathnormal">a</span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mord mathnormal">i</span><span class="mord mathnormal">t</span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span><span class="mclose">?</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">></span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord mathnormal">c</span><span class="mord mathnormal">d</span><span class="mord mathnormal">a</span><span class="mord mathnormal">x</span><span class="mord mathnormal">i</span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span><span class="mord mathnormal">m</span><span class="mord mathnormal" style="margin-right:0.07153em;">C</span><span class="mord mathnormal">a</span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mord mathnormal">i</span><span class="mord mathnormal">t</span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span><span class="mclose">?</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">></span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.9805em;vertical-align:-0.2861em;"></span><span class="mord mathnormal">b</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">oc</span><span class="mord mathnormal" style="margin-right:0.03148em;">k</span><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="mord mathnormal">es</span><span class="mord mathnormal">h</span><span class="mord">‘‘‘</span><span class="mord cjk_fallback">对于轴对称网格,</span><span class="mord mathnormal">m</span><span class="mord mathnormal">o</span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mord mathnormal">in</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal">Wa</span><span class="mord mathnormal" style="margin-right:0.01968em;">ll</span><span class="mord cjk_fallback">面片被用作对称轴(参见图</span><span class="mord">2.24</span><span class="mord cjk_fallback">)。此外,单个</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal">ro</span><span class="mord mathnormal">n</span><span class="mord mathnormal">t</span><span class="mord mathnormal">A</span><span class="mord mathnormal">n</span><span class="mord mathnormal">d</span><span class="mord mathnormal" style="margin-right:0.05017em;">B</span><span class="mord mathnormal">a</span><span class="mord mathnormal">c</span><span class="mord mathnormal" style="margin-right:0.03148em;">k</span><span class="mord cjk_fallback">面片将被分割,并充当楔形体的两个边界(</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal">ro</span><span class="mord mathnormal">n</span><span class="mord mathnormal">t</span><span class="mord mathnormal">A</span><span class="mord mathnormal">n</span><span class="mord mathnormal">d</span><span class="mord mathnormal" style="margin-right:0.05017em;">B</span><span class="mord mathnormal">a</span><span class="mord mathnormal">c</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03148em;">k</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.1514em;"><span style="top:-2.55em;margin-left:-0.0315em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">n</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord cjk_fallback">与</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal">ro</span><span class="mord mathnormal">n</span><span class="mord mathnormal">t</span><span class="mord mathnormal">A</span><span class="mord mathnormal">n</span><span class="mord mathnormal">d</span><span class="mord mathnormal" style="margin-right:0.05017em;">B</span><span class="mord mathnormal">a</span><span class="mord mathnormal">c</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.03148em;">k</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.1514em;"><span style="top:-2.55em;margin-left:-0.0315em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">p</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.2861em;"><span></span></span></span></span></span></span><span class="mord mathnormal">os</span><span class="mord cjk_fallback">)。在命令行中输入的参数反映了这一点:</span><span class="mord">‘‘‘</span><span class="mord mathnormal">ba</span><span class="mord mathnormal">s</span><span class="mord mathnormal">h</span><span class="mclose">?</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">></span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.7778em;vertical-align:-0.0833em;"></span><span class="mord mathnormal" style="margin-right:0.03148em;">mak</span><span class="mord mathnormal">e</span><span class="mord mathnormal">A</span><span class="mord mathnormal">x</span><span class="mord mathnormal">ia</span><span class="mord mathnormal" style="margin-right:0.10903em;">lM</span><span class="mord mathnormal">es</span><span class="mord mathnormal">h</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord mathnormal">a</span><span class="mord mathnormal">x</span><span class="mord mathnormal">i</span><span class="mord mathnormal">s</span><span class="mord mathnormal">m</span><span class="mord mathnormal">o</span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mord mathnormal">in</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal">Wa</span><span class="mord mathnormal" style="margin-right:0.01968em;">ll</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord mathnormal" style="margin-right:0.02691em;">w</span><span class="mord mathnormal">e</span><span class="mord mathnormal">d</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal">ro</span><span class="mord mathnormal">n</span><span class="mord mathnormal">t</span><span class="mord mathnormal">A</span><span class="mord mathnormal">n</span><span class="mord mathnormal">d</span><span class="mord mathnormal" style="margin-right:0.05017em;">B</span><span class="mord mathnormal">a</span><span class="mord mathnormal">c</span><span class="mord mathnormal" style="margin-right:0.03148em;">k</span><span class="mord">‘‘‘</span><span class="mord cjk_fallback">该工具将创建一个新的时间目录(在本例中为</span><span class="mord">0.005</span><span class="mord cjk_fallback">)来存储转换后的网格。如果创建未按预期工作,则只需删除此目录,并再次恢复基本网格。案例目录现在应包含如下所示的文件夹:</span><span class="mord">‘‘‘</span><span class="mord mathnormal">ba</span><span class="mord mathnormal">s</span><span class="mord mathnormal">h</span><span class="mclose">?</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">></span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">s</span><span class="mord">00.005</span><span class="mord mathnormal">co</span><span class="mord mathnormal">n</span><span class="mord mathnormal">s</span><span class="mord mathnormal">t</span><span class="mord mathnormal">an</span><span class="mord mathnormal">t</span><span class="mord mathnormal">sys</span><span class="mord mathnormal">t</span><span class="mord mathnormal">e</span><span class="mord mathnormal">m</span><span class="mord">‘‘‘</span><span class="mord cjk_fallback">此时,网格已弯曲成</span><span class="mord">5°</span><span class="mord cjk_fallback">楔形,如图</span><span class="mord">2.25</span><span class="mord cjk_fallback">所示。但是,</span><span class="mord mathnormal">m</span><span class="mord mathnormal">o</span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mord mathnormal">in</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal">Wa</span><span class="mord mathnormal" style="margin-right:0.01968em;">ll</span><span class="mord cjk_fallback">面片中的面仍然存在,但它们现在被挤压为面面积接近于零的面。</span><span class="mord mathnormal" style="margin-right:0.03148em;">mak</span><span class="mord mathnormal">e</span><span class="mord mathnormal">A</span><span class="mord mathnormal">x</span><span class="mord mathnormal">ia</span><span class="mord mathnormal" style="margin-right:0.10903em;">lM</span><span class="mord mathnormal">es</span><span class="mord mathnormal">h</span><span class="mord cjk_fallback">变换点位置,但不改变网格连接。因此,对称面片没有指定面(</span><span class="mord mathnormal">n</span><span class="mord mathnormal" style="margin-right:0.13889em;">F</span><span class="mord mathnormal">a</span><span class="mord mathnormal">ces</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord">0</span><span class="mord cjk_fallback">),必须移除。</span><span class="mclose">!</span><span class="mopen">[</span><span class="mord cjk_fallback">图</span><span class="mord">2.25</span><span class="mord cjk_fallback">:</span><span class="mord mathnormal" style="margin-right:0.03148em;">mak</span><span class="mord mathnormal">e</span><span class="mord mathnormal">A</span><span class="mord mathnormal">x</span><span class="mord mathnormal">ia</span><span class="mord mathnormal" style="margin-right:0.10903em;">lM</span><span class="mord mathnormal">es</span><span class="mord mathnormal">h</span><span class="mord cjk_fallback">楔形块变换前后的</span><span class="mord">2</span><span class="mord mathnormal" style="margin-right:0.02778em;">D</span><span class="mord cjk_fallback">型腔网格</span><span class="mclose">]</span><span class="mopen">(</span><span class="mord mathnormal">h</span><span class="mord mathnormal">ttp</span><span class="mord mathnormal">s</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">:</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord">//</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal">a</span><span class="mord mathnormal">ee</span><span class="mord">0</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:0.8389em;vertical-align:-0.1944em;"></span><span class="mord">1253397841.</span><span class="mord mathnormal">cos</span><span class="mord">.</span><span class="mord mathnormal">a</span><span class="mord mathnormal">p</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal">c</span><span class="mord mathnormal">h</span><span class="mord mathnormal">e</span><span class="mord mathnormal">n</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal">d</span><span class="mord mathnormal">u</span><span class="mord">.</span><span class="mord mathnormal">m</span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span><span class="mord mathnormal" style="margin-right:0.03588em;">q</span><span class="mord mathnormal">c</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">o</span><span class="mord mathnormal">u</span><span class="mord mathnormal">d</span><span class="mord">.</span><span class="mord mathnormal">co</span><span class="mord mathnormal">m</span><span class="mord">/</span><span class="mord mathnormal" style="margin-right:0.02691em;">w</span><span class="mord mathnormal">i</span><span class="mord mathnormal" style="margin-right:0.04398em;">z</span><span class="mord mathnormal">im</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord">/202212030308697.</span><span class="mord mathnormal">p</span><span class="mord mathnormal">n</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mclose">)</span><span class="mord cjk_fallback">在这种情况下,建议使用</span><span class="mord mathnormal">co</span><span class="mord mathnormal" style="margin-right:0.01968em;">ll</span><span class="mord mathnormal">a</span><span class="mord mathnormal">p</span><span class="mord mathnormal">se</span><span class="mord mathnormal" style="margin-right:0.05764em;">E</span><span class="mord mathnormal">d</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal">es</span><span class="mord cjk_fallback">工具。它需要两个必需的命令行参数:边长和合并角:</span><span class="mord">‘‘‘</span><span class="mord mathnormal">ba</span><span class="mord mathnormal">s</span><span class="mord mathnormal">h</span><span class="mclose">?</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">></span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord mathnormal">co</span><span class="mord mathnormal" style="margin-right:0.01968em;">ll</span><span class="mord mathnormal">a</span><span class="mord mathnormal">p</span><span class="mord mathnormal">se</span><span class="mord mathnormal" style="margin-right:0.05764em;">E</span><span class="mord mathnormal">d</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal">es</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel"><</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal">e</span><span class="mord mathnormal">d</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">e</span><span class="mord mathnormal">n</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal">t</span><span class="mord mathnormal">h</span><span class="mopen">[</span><span class="mord mathnormal">m</span><span class="mclose">]</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">><</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal">m</span><span class="mord mathnormal" style="margin-right:0.02778em;">er</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal">e</span><span class="mord mathnormal">an</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">e</span><span class="mopen">[</span><span class="mord mathnormal">d</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal">rees</span><span class="mclose">]</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">></span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.6944em;"></span><span class="mord">‘‘‘</span><span class="mord cjk_fallback">在许多应用中,边长为</span></span></span></span>1 × 10^{−8}$米,合并角为179°时,可以正确识别和移除最近塌陷的面。在网格边长比例极小的某些情况下,可能需要较小的边长以避免误报和无意中删除有效边。对于本示例,使用所示参数执行collapseEdges不会出现问题。
```bash
?> collapseEdges -latestTime 1e-8 179
对于一些最终的内务处理,建议从边界列表中删除现在为空的面片。打开constant/polyMesh/boundary并删除movingWall与frontAndBack条目。请注意,它们被列为包含零个面:nFaces 0;。将边界列表大小变更为3,以反映这两项删除。边界文件现在应类似于:
3
(
fixedWalls
{
type wall;
nFaces 60;
startFace 760;
}
frontAndBack_pos
{
type wedge;
nFaces 400;
startFace 820;
}
frontAndBack_neg
{
type wedge;
nFaces 400;
startFace 1220;
}
)
此时,可以使用autoPatch工具将fixedWalls面片分割为3个单独的面片。这将查看连续的面片,并尝试根据给定的特征角度确定适当的位置来分割它。
在这种情况下,任何形成大于30°角的patch边都可以被分割以形成新的patch。在分配边界条件时,这提供了更大的灵活性。
?> autoPatch -latestTime 30
分割后将重命名面片。-latestTime标志将仅读取可用的最新时间步。分割网格面会储存在另一个时间步长目录中,而不是覆写时间步长。最后,应使用checkMesh工具检查网格是否存在错误,这应被视为最佳实践的一般规则:更改网格时始终运行checkMesh。
可以在目录WM_PROJECT_DIR/applications/utilities/mesh中找到处理网格操作的实用程序应用程序(或只是简短的实用程序)。网格实用程序分为以下类别:生成、操纵、推进和转换。这种分类在最新版本中完全没有改变。生成网格并将其从不同格式转换为OpenFOAM格式已在第2.2节和第2.3节中描述。本节介绍如何在生成基础网格后操纵网格以及诸如网格细化等高级操作。
2.4.1 按指定标准细化网格
在此示例中,网格细化应用程序refineHexMesh用于细化interFoam解算器的damBreak教程的网格。这样做的目的是细化初始自由表面周围的区域,其中两相标志场(\alpha_{water}\nabla(\alpha_{water}\alpha_{water}FOAM_TUTORIALS/multiphase/interFoam/laminar/damBreak . ?> cd damBreak ?> blockMesh ?> setFields
现在用blockMesh生成网格,并使用setFields前处理实用程序设置$\alpha_{water}$场。 setfields实用工具在3.2节中进行了描述。 基本的计算工具foamCalc可以用来计算和存储$\alpha_{water}$的梯度。
```bash
?> foamCalc magGrad alpha.water
这将把梯度幅度的以单元为中心的标量场存储在名为magGradalphaWater.的初始时间目录0中。 要使用refineMesh应用程序根据梯度大小细化网格,必须将该实用程序的配置字典文件复制到dambreake案例的系统目录中。
?> cp <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.02778em;">FO</span><span class="mord mathnormal">A</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3283em;"><span style="top:-2.55em;margin-left:-0.109em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">A</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord mathnormal" style="margin-right:0.13889em;">PP</span><span class="mord">/</span><span class="mord mathnormal">u</span><span class="mord mathnormal">t</span><span class="mord mathnormal">i</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">i</span><span class="mord mathnormal">t</span><span class="mord mathnormal">i</span><span class="mord mathnormal">es</span><span class="mord">/</span><span class="mord mathnormal">m</span><span class="mord mathnormal">es</span><span class="mord mathnormal">h</span><span class="mord">/</span><span class="mord mathnormal">mani</span><span class="mord mathnormal">p</span><span class="mord mathnormal">u</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">a</span><span class="mord mathnormal">t</span><span class="mord mathnormal">i</span><span class="mord mathnormal">o</span><span class="mord mathnormal">n</span><span class="mord">/</span><span class="mord mathnormal">re</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal">in</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="mord mathnormal">es</span><span class="mord mathnormal">h</span><span class="mord">/</span><span class="mord mathnormal">re</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal">in</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="mord mathnormal">es</span><span class="mord mathnormal">h</span><span class="mord mathnormal" style="margin-right:0.02778em;">D</span><span class="mord mathnormal">i</span><span class="mord mathnormal">c</span><span class="mord mathnormal">t</span><span class="mord mathnormal">sys</span><span class="mord mathnormal">t</span><span class="mord mathnormal">e</span><span class="mord mathnormal">m</span><span class="mord">/</span><span class="mclose">?</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">></span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">ssys</span><span class="mord mathnormal">t</span><span class="mord mathnormal">e</span><span class="mord mathnormal">m</span><span class="mord">/</span><span class="mord mathnormal">co</span><span class="mord mathnormal">n</span><span class="mord mathnormal">t</span><span class="mord mathnormal">ro</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal" style="margin-right:0.02778em;">D</span><span class="mord mathnormal">i</span><span class="mord mathnormal">c</span><span class="mord mathnormal">t</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord mathnormal">c</span><span class="mord mathnormal">h</span><span class="mord mathnormal">e</span><span class="mord mathnormal">m</span><span class="mord mathnormal">esre</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal">in</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="mord mathnormal">es</span><span class="mord mathnormal">h</span><span class="mord mathnormal" style="margin-right:0.02778em;">D</span><span class="mord mathnormal">i</span><span class="mord mathnormal">c</span><span class="mord mathnormal">t</span><span class="mord mathnormal">d</span><span class="mord mathnormal">eco</span><span class="mord mathnormal">m</span><span class="mord mathnormal">p</span><span class="mord mathnormal">ose</span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mord mathnormal">a</span><span class="mord mathnormal" style="margin-right:0.02778em;">rD</span><span class="mord mathnormal">i</span><span class="mord mathnormal">c</span><span class="mord mathnormal">t</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord mathnormal">o</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">u</span><span class="mord mathnormal">t</span><span class="mord mathnormal">i</span><span class="mord mathnormal">o</span><span class="mord mathnormal">n</span><span class="mord mathnormal">se</span><span class="mord mathnormal" style="margin-right:0.13889em;">tF</span><span class="mord mathnormal">i</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">d</span><span class="mord mathnormal" style="margin-right:0.02778em;">sD</span><span class="mord mathnormal">i</span><span class="mord mathnormal">c</span><span class="mord mathnormal">t</span><span class="mord">‘‘‘</span><span class="mord cjk_fallback">在</span><span class="mord mathnormal">sys</span><span class="mord mathnormal">t</span><span class="mord mathnormal">e</span><span class="mord mathnormal">m</span><span class="mord cjk_fallback">目录中的配置中,</span><span class="mord mathnormal">re</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal">in</span><span class="mord mathnormal">eHe</span><span class="mord mathnormal">x</span><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="mord mathnormal">es</span><span class="mord mathnormal">h</span><span class="mord cjk_fallback">对某个网格集中的所有网格进行细化。</span><span class="mord">‘‘‘</span><span class="mord mathnormal">c</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord">+</span><span class="mord">//</span><span class="mord mathnormal" style="margin-right:0.07153em;">C</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.01968em;">ll</span><span class="mord mathnormal">s</span><span class="mord mathnormal">t</span><span class="mord mathnormal">ore</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal">in</span><span class="mord mathnormal">e</span><span class="mpunct">;</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord mathnormal">nam</span><span class="mord mathnormal">eo</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal">ce</span><span class="mord mathnormal" style="margin-right:0.01968em;">ll</span><span class="mord mathnormal">se</span><span class="mord mathnormal">t</span><span class="mord mathnormal">se</span><span class="mord mathnormal">t</span><span class="mord mathnormal">c</span><span class="mord">0</span><span class="mpunct">;</span><span class="mspace" style="margin-right:0.1667em;"></span><span class="mord">‘‘‘</span><span class="mord cjk_fallback">创建此</span><span class="mord mathnormal" style="margin-right:0.07153em;">C</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.05764em;">llS</span><span class="mord mathnormal">e</span><span class="mord mathnormal">t</span><span class="mord cjk_fallback">时,将存储在</span><span class="mord mathnormal">co</span><span class="mord mathnormal">n</span><span class="mord mathnormal">s</span><span class="mord mathnormal">t</span><span class="mord mathnormal">an</span><span class="mord mathnormal">t</span><span class="mord">/</span><span class="mord mathnormal">p</span><span class="mord mathnormal">o</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span><span class="mord mathnormal">m</span><span class="mord mathnormal">es</span><span class="mord mathnormal">h</span><span class="mord cjk_fallback">中,</span><span class="mord mathnormal" style="margin-right:0.00773em;">R</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal">in</span><span class="mord mathnormal">eHe</span><span class="mord mathnormal">x</span><span class="mord mathnormal">m</span><span class="mord mathnormal">es</span><span class="mord mathnormal">h</span><span class="mord cjk_fallback">将使用它来细化单元格。在本例中,</span><span class="mord mathnormal">t</span><span class="mord mathnormal">o</span><span class="mord mathnormal">p</span><span class="mord mathnormal">o</span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord mathnormal">e</span><span class="mord mathnormal">t</span><span class="mord cjk_fallback">用于生成</span><span class="mord mathnormal">ce</span><span class="mord mathnormal" style="margin-right:0.05764em;">llS</span><span class="mord mathnormal">e</span><span class="mord mathnormal">t</span><span class="mord cjk_fallback">。这要求</span><span class="mord mathnormal">t</span><span class="mord mathnormal">o</span><span class="mord mathnormal">p</span><span class="mord mathnormal">o</span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord mathnormal">e</span><span class="mord mathnormal">t</span><span class="mord mathnormal" style="margin-right:0.02778em;">D</span><span class="mord mathnormal">i</span><span class="mord mathnormal">c</span><span class="mord mathnormal">t</span><span class="mord cjk_fallback">存在于系统目录中并正确配置。因此,随后会复制并更改现有的文件。</span><span class="mord">‘‘‘</span><span class="mord mathnormal">ba</span><span class="mord mathnormal">s</span><span class="mord mathnormal">h</span><span class="mclose">?</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">></span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.625em;vertical-align:-0.1944em;"></span><span class="mord mathnormal">c</span><span class="mord mathnormal">p</span></span></span></span>FOAM_APP/utilities/mesh/manipulation/topoSet/topoSetDict system/
Toposetdict的示例操作子字典必须由以下内容替换:
actions
(
{
name c0;
type cellSet;
action new;
source fieldToCell;
sourceInfo
{
fieldName magGradalpha1;
min 20;
max 100;
}
}
);
现在可以根据System/Toposetdict中的定义生成cellset:
?> topoSet
?> refineHexMesh c0
当网格现在使用Paraview查看时,自由表面的区域现在应该有额外的分辨率。
2.4.2 变换点
在OpenFOAM网格格式中,与网格的比例和位置有关的唯一信息位于点位置向量中。如前所述,所有剩余的存储的网格信息是纯粹基于连通性的。也就是说,网格大小、位置和方向可以通过单独变换点位置来改变。为此,transformPoints网格实用程序随OpenFOAM提供。由于此实用程序相对简单,因此只显示了所需的语法。变换网格时最常用的选项是-rotate、-translate和-scale选项。
也可以在括号周围使用双引号而不是单引号。 执行任务的顺序是硬编码的,用户不能更改。 如果要确保在转换之前执行缩放,请运行TransformPoints两次。
- scale。按指定的标量量在任意或所有基本方向上缩放网格的点。-scale '(1.0 1.0 1.0)'不会变更点位置,而-scale '(2.0 2.0 2.0)'会在所有方向上将点位置均匀加倍。任何非均匀缩放都将沿给定方向拉伸或压缩网格。
- translate。按给定向量移动网格,有效地将此向量添加到网格中的每个点位置向量。
- rotate。旋转网格。旋转由输入向量定义。网格将经历使用第二个向量定向第一个向量所需的旋转。旋转网格时,也可以通过添加
-rotateFields选项来旋转任何初始或边界向量与张量值。
这三个点转换的语法如下所示。
?> transformPoints -scale '(x y z)'
?> transformPoints -translate '(x y z)'
?> transformPoints -rotateFields -rotate '( (x0 y0 z0) (x1 y1 z1) )'
2.4.3 镜像网格
有时,用对称平面生成网格,然后执行镜面反射比在一个步骤中网格化整个几何结构更容易。 mirrorMesh实用程序正是这样做的。 关于镜像进程本身的所有参数都是从位于system/mirrorMeshDict中的字典中读取的。
为了成功镜像网格,镜像平面必须是平面。在本例中,四分之一网格被镜像到全域中。首先,下面的固析例必须复制到选择的目录中并重新命名,以防以后混淆。mirrorMeshDict需要从现有案例复制到案例系统目录中。
?> cp -r <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.02778em;">FO</span><span class="mord mathnormal">A</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3283em;"><span style="top:-2.55em;margin-left:-0.109em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right:0.13889em;">T</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord mathnormal" style="margin-right:0.10903em;">U</span><span class="mord mathnormal" style="margin-right:0.00773em;">TOR</span><span class="mord mathnormal" style="margin-right:0.07847em;">I</span><span class="mord mathnormal">A</span><span class="mord mathnormal">L</span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord">/</span><span class="mord mathnormal">s</span><span class="mord mathnormal">t</span><span class="mord mathnormal">ress</span><span class="mord mathnormal">A</span><span class="mord mathnormal">na</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">ys</span><span class="mord mathnormal">i</span><span class="mord mathnormal">s</span><span class="mord">/</span><span class="mord mathnormal">so</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">i</span><span class="mord mathnormal">d</span><span class="mord mathnormal" style="margin-right:0.02778em;">D</span><span class="mord mathnormal">i</span><span class="mord mathnormal">s</span><span class="mord mathnormal" style="margin-right:0.01968em;">pl</span><span class="mord mathnormal">a</span><span class="mord mathnormal">ce</span><span class="mord mathnormal">m</span><span class="mord mathnormal">e</span><span class="mord mathnormal">n</span><span class="mord mathnormal" style="margin-right:0.13889em;">tF</span><span class="mord mathnormal">o</span><span class="mord mathnormal">am</span><span class="mord">/</span><span class="mord mathnormal" style="margin-right:0.01968em;">pl</span><span class="mord mathnormal">a</span><span class="mord mathnormal">t</span><span class="mord mathnormal">eHo</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">e</span><span class="mord">.</span><span class="mclose">?</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">></span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord mathnormal">m</span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mord mathnormal" style="margin-right:0.01968em;">pl</span><span class="mord mathnormal">a</span><span class="mord mathnormal">t</span><span class="mord mathnormal">eHo</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">e</span><span class="mord mathnormal">mi</span><span class="mord mathnormal" style="margin-right:0.02778em;">rror</span><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="mord mathnormal">es</span><span class="mord mathnormal">h</span><span class="mord mathnormal" style="margin-right:0.05764em;">E</span><span class="mord mathnormal">x</span><span class="mord mathnormal">am</span><span class="mord mathnormal" style="margin-right:0.01968em;">pl</span><span class="mord mathnormal">e</span><span class="mclose">?</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">></span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.8889em;vertical-align:-0.1944em;"></span><span class="mord mathnormal">c</span><span class="mord mathnormal">d</span><span class="mord mathnormal">mi</span><span class="mord mathnormal" style="margin-right:0.02778em;">rror</span><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="mord mathnormal">es</span><span class="mord mathnormal">h</span><span class="mord mathnormal" style="margin-right:0.05764em;">E</span><span class="mord mathnormal">x</span><span class="mord mathnormal">am</span><span class="mord mathnormal" style="margin-right:0.01968em;">pl</span><span class="mord mathnormal">e</span><span class="mclose">?</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">></span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.7778em;vertical-align:-0.1944em;"></span><span class="mord mathnormal">c</span><span class="mord mathnormal">p</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:0.4306em;"></span><span class="mord mathnormal" style="margin-right:0.02778em;">r</span></span></span></span>FOAM_APP/utilities/mesh/manipulation/mirrorMesh/mirrorMeshDict system/
下一步是定义将作为镜像平面的平面。这样的平面可以由原点和法向向量定义,在mirrorMeshDict中如下所示。发生镜像的patch会自动移除。

pointAndNormalDict
{
basePoint (0 0 0);
normalVector (0 -1 0);
}
正确定义后,可以执行mirrorMesh,并检查网格是否存在错误:
?> mirrorMesh
?> checkMesh
这会产生半网格。对于第二次镜像,必须更改字典以说明不同的镜像平面:
pointAndNormalDict
{
basePoint (0 0 0);
normalVector (-1 0 0);
}
再次运行mirrorMesh并使用checkMesh检查网格本身是否存在任何错误:
?> mirrorMesh
?> checkMesh
这将生成一个全域网格。
有很多开源应用程序可用于设计计算域几何形状以及生成网格。另一方面,也有用于相同目的的商业解决方案。几何图形定义和网格生成有时涉及冗长的工作流,直到几何图形减少到模拟可接受的级别,并且生成的网格具有足够的质量。对于简单的情况,例如验证,blockMesh仍然是许多用户首选的网格生成工具。自动网格生成解决方案(如snappyHexMesh、cfMesh、foamHexMesh和engrid)降低了网格生成的复杂性和持续时间,但仍涉及处理不同的网格生成参数。上述应用程序随其详细文档分发,因此本章旨在提供OpenFOAM中网格的组成方式信息,以及使用blockMesh和snappyHexMesh生成网格的附加信息,以扩展当前可用的文档。
- Sept. 2014. Url: http://www.sourceflux.de/blog/adding-source-terms-equations-fvoptions/.
- May 2015. Url: http://www.sourceflux.de/blog/a-changing-cell-set-in-openfoam/.
- J. Höpken and T. Maric. Feature handling in snappyHexMesh. Url: www.sourceflux.de/blog/snappyhexmesh-snapping-edges.
- OpenFOAM User Guide. OpenCFD limited. 2016.
- E. de Villiers. 7 th OpenFOAM Workshop: snappyHexMesh Training. Url: http://www.openfoamworkshop.org/2012/downloads/Training/EugenedeVilliers/EugenedeVilliers-TrainingSlides.tgz (visited on 12/2013).
本章将介绍 OpenFOAM 模拟的结构以及边界条件和初始条件的定义。
注:本章的模拟测试用例可在第 3 章子目录下的示例案例库中找到。
OpenFOAM仿真文件是一个目录,其中包含存储在不同子目录中的一组文件。一些文件用于配置和控制仿真,其他文件用于存储生成的仿真数据。通常,OpenFOAM模拟案例的基于文件的组织相对简单易用:可以使用文本编辑器轻松编辑配置文件。使用基于文件的组织还有一个优点:可以轻松地参数化仿真。
使用icoFoam不可压缩Navier-Stokes求解器使用的方腔顶盖流教程案例解释了OpenFOAM案例(模拟)的标准组成。图3.1显示了型腔设置的示意图。
Case目录中存在icoFoam不需要的其他输入文件,它们由预处理实用程序使用。通常,所需输入字典的数量随着求解器复杂性的增加而增加。
下面的方腔案例的子目录列表显示了模拟文件的组织方式:
?> cd $FOAM_TUTORIALS/incompressible/icoFoam/cavity
?> ls *
0:
p U
constant:
polyMesh transportProperties
system:
controlDict fvSchemes fvSolution
0、constant和system目录是OpenFOAM模拟案例必须包含的标准目录。0目录保存应用于物理场的初始条件和边界条件。特定求解器使用的每个物理场都由一个以该物理场命名的文本文件表示。对方腔案例的问题,模拟中使用的场是压力场和速度场,这些场的定义如第3.2节所示。
随着模拟的进行,求解器应用程序将结果模拟数据写入案例目录的新子目录。这些目录就是所谓的时间步目录,该目录中的文件是根据模拟时间值命名的。它们不仅包含已在0/目录中定义的那些物理场变量,还包含解算器的辅助变量,如体积通量phi。
尽管icoFoam求解器使用压力p场和速度U场的初始值开始模拟,但FVM在方程离散过程中会使用体积通量场(Phi)(有关详细信息,请参见第1章)。因此,时间步长目录将保存由求解器应用程序计算的体积通量场phi。
除了时间点目录之外,还可以写入其他模拟数据:
- 通过求解器应用程序(如体积通量phi)
- 通过通过与求解器一起运行的function object
- 在模拟完成之后,作为后处理的结果
Constant目录存储整个模拟过程中保持不变的模拟数据。这通常包含polyMesh子目录中的网格数据,以及各种配置文件:
transportProperties。输运数据turbulenceProperties。湍流模型数据dynamicMeshDict。动网格控制数据
并非所有上述配置文件都存在于方腔实例的constant目录中。缺少的是icoFoam不需要的turbulenceProperties字典。需要提供哪些附加字典,这取决于选定的求解器应用程序。如果在缺少必要输入数据的情况下在案例目录中执行求解器,则会向用户提示错误消息,通知用户缺少或定义了错误的字典、字典参数或物理场变量。
如果求解器应用程序使用了动态网格功能,若网格节点位置或网格拓扑发生更改,则新的polyMesh文件夹也会写入每个时间点目录。第13章讨论了OpenFOAM的动态网格功能。
OpenFOAM中的配置文件通常称为字典文件,甚至简称为字典。这种命名是由于它们在源代码中的使用,源代码基于IODICTIONARY类。
这些方法见第1章。它还可能包含用于配置不同预处理和后处理应用程序(如设置字段)的字典。system目录中最重要的字典是controlDict,其控制与解算器运行时间相关的所有参数,以及将求解数据写入到case目录的频率。controlDict中定义的所有参数与用于模拟的求解器无关。有关使用controlDict控制模拟运行的更多信息,请参见第3.4节。[5]对controlDict中的参数进行了相当广泛的讨论,第3.4.1节对其中一些参数进行了解释。
0OpenFOAM simulation是一个包含用于配置模拟的不同子目录和文件的目录。这种OpenFOAM模拟的文件结构使得设置边界和初始条件非常简单。每个对模拟重要的物理量(压力、温度、速度场等)都有其文件,存储在0目录中:属于模拟第一个时间步的目录。本节介绍如何在这些文件中实际应用第1.3节中的边界条件和初始条件。根据场的张量秩(标量、向量、张量),使用稍微不同的语法设置它们各自的值。本次讨论仅限于案例配置;第1.3节和第10章分别讨论了边界条件的数值和设计细节。顾名思义,边界条件定义网格边界处的场值。初始条件指内部场变量的初始值。图1.12显示了内部值和边界值之间的差异示意图。
有关计算网格的更多信息,请参见第2.1章。第1章讨论了数值方法的基本原理。读者应该在一定程度上了解这两个主题。
在仔细查看如何定义边界条件文件之前,必须将用icoFoam模拟的方腔实例复制到选择的位置。要设置方腔仿真实例的基本边界条件,需要复制并重命名仿真实例目录:
?> cp -r $FOAM_TUTORIALS/incompressible/icoFoam/cavity/cavity cavityOscillatingU
?> cd cavityOscillatingU
列出0/目录表明定义了两个不同的物理场:p和U。这两个文件都可以直接从命令行中使用任何文本编辑器进行编辑。可以使用以下命令将压力边界条件文件的相关行打印到屏幕上:
?> cat 0/p | tail -n 23 | head -21
dimensions [0 2 -2 0 0 0 0];
internalField uniform 0;
boundaryField
{
movingWall
{
type zeroGradient;
}
fixedWalls
{
type zeroGradient;
}
frontAndBack
{
type empty;
}
}
内容显示边界条件文件的三个顶级对象:dimensions、internalField和boundaryField。第一个对象是一组标量维度(dimsionSet),用于定义物理场的量纲。每个标量对应于特殊SI单位的幂,如维度集(dimensionSet.H)的声明源文件中所定义。
// 定义维度指数名称的枚举
enum dimensionType
{
MASS, // 质量 kg
LENGTH, // 长度 m
TIME, // 时间 s
TEMPERATURE, // 温度 K
MOLES, // 物质的量 mol
CURRENT, // 电流 A
LUMINOUS_INTENSITY // 光强 Cd
};
另一个对象是internalField,其定义了物理场的初始条件。请注意,这不包括由最后一个子字典:boundaryField定义的边界。在本例中,所有网格值都设置为0。还可以在每个网格格的基础上定义初始值,这反过来要求用户为每个网格组成一个包含所需值的列表。该列表中的网格数量必须与网格中的单元数量相同,其组成如[5]所述。最后,在boundaryField子目录中定义边界条件。必须为每个patch和每个物理场指定边界条件。因此,每个patch的边界条件在boundaryField字典的子字典中定义。
3.2.1 设置边界条件
OpenFOAM的官方发布已经附带了许多边界条件。在案例目录中执行foamHelp命令时,会提供所有可用边界条件的列表。 它说明了场类型,只显示了与相应场兼容的边界条件。结果列表中显示的一些边界条件非常一般,而其他边界条件则非常特定于问题。对于速度场U,可以用以下方式调用:
?> foamHelp boundary -field U
foamHelp要求在检查可用边界条件时生成网格。作为定义边界条件的一个小例子,使用了之前复制的cavityOscillatingU案例。在本例中,将速度场U的动壁边界条件更改为确保速度随时间振荡的边界条件(图3.1)。要设置振荡速度,我们将使用codedFixedValue边界条件。这种边界条件允许其用户编写C++代码,定义边界条件如何运行。这个C++代码然后在上面的编码边界条件的C++代码片段中,我们重载了OpenFOAM场赋值操作符,以将速度向量设置为cos(πt)(1,0,0),使其每秒切换一次方向。除了上述对U场的改变外,还必须延长模拟时间,以便可以可视化几个速度振荡周期。为此,必须更改system/control Dict字典:将条目endTime从0.5修改为4.0。所有需要的调整都已完成,更改后的边界条件可以使用icoFoam解算器进行测试。在执行此操作之前,必须使用block Mesh工具生成网格:OpenFOAM编译成仿真实例中的库,存储在dynamicCode子文件夹中。该库动态链接到求解器应用程序,并在模拟中使用。由于它是实现边界条件的C++代码,边界条件的用户应该知道如何在OpenFOAM中用标量、向量或张量来执行它们各自物理场的基本操作。
本书第二部分介绍了C++编程知识。一般来说,关于边界条件、function object和其他OpenFOAM组件的使用信息可以在扩展代码指南中找到,也在第5章中介绍。或者在OpenFOAM源代码中读取边界条件的头文件通常更快。必须使用文本编辑器打开文件中codedFixedValue边界条件的声明。该文件位于:
$FOAM_SRC/finiteVolume/fields/fvPatchFields/derived/codedFixedValue/codedFixedValueFvPatchField.H
头文件顶部的注释部分的Description部分包含边界条件用法的描述,我们在这里针对movingWall边界进行修改:
movingWall
{
type codedFixedValue;
value uniform (0 0 0);
name oscillatingFixedValue; // name of generated BC
code
#{
operator==(Foam::cos(this-> db().time().value() * M_PI)*vector(1,0,0));
#};
}
在上面的边界条件的C++代码片段中,我们重载了OpenFOAM场赋值操作符,以将速度向量设置为,使其每秒切换一次方向。除了上述对速度场的改变外,还必须延长模拟时间,以便可以观察几个速度振荡周期。为此,必须更改system/controlDict字典:将条目endTime从0.5修改为4.0。所有需要的调整都已完成,更改后的边界条件可以使用icoFoam解算器进行测试。在执行此操作之前,必须使用blockMesh工具生成网格:
?> blockMesh
?> icoFoam
可以使用paraView实现速度场的可视化。
注:要使用ParaView查看OpenFOAM的计算结果,可以创建一个扩展名为.foam的空文件,然后利用ParaView打开。
在振荡边界条件的驱动下,内部流动发生脉动。
在选择边界条件时总是需要仔细考虑,特别是在将结果与实验(验证)或精确解(验证)进行比较时。在 foam _ tutorial cases 教程中包含了使用不同边界条件的模拟示例。教程案例可以是一个使用不同的边界条件有用的信息来源。
3.2.2 设置初始条件
在这一节中,概述了如何设置模拟的初始条件。初始条件在模拟开始时定义内部物理场的值。有各种不同的工具用于用户指定初始化物理场。第八章提供有关如何开发新的前后处理应用的资料。
注:设定初始条件(IC)称为前处理。
初始条件可以是微不足道的,就像方腔案例一样:将初始内部速度和压力设置为统一的向量值0。在第一个时间步长之后,计算的流动解通常与初始设置的流动解有很大不同。对于定常的单相不可压缩流动,初始条件可以看作是加速收敛到定常的初始条件。如果这个猜测离最终结果,可能会出现计算发散。
在其他情况下,初始条件是至关重要的,因为它们决定了场如何从初始值在时间上演变。可压缩流动模拟在很大程度上依赖于初始压力、温度和/或密度来正确地计算状态方程。不可压缩的多相模拟需要非常精确的用于分离流体相的相指示器场的初始值。初始相位指示器中的较大误差会导致更大的曲率近似误差,从而导致很强的数值不稳定性和可能的灾难性失败。
如前所述,空腔示例情况对初始条件的定义相对宽容。对初始条件有特殊要求的情况是使用interFoam解算器模拟的damBreak情况。求解器interFoam是一个两相流动求解器,使用代数流体体积方法区分两个不可混溶和不可压缩的流体相。为此,引入了一个新的标量场:alpha.water。本例中的气体和液相的alpha.water值分别为0和1。对于第一个示例,将向damBreak案例添加一个水滴,如图3.2所示。
首先,创建damBreak教程案例的副本,并将案例重命名:
?> run
?> cp -r FOAM_TUTORIALS/multiphase/interFoam/laminar/damBreak/damBreak damBreakWithDrop
原始场值通常保存在子文件夹0中,或保存在0文件夹中的*.orig字段文件中。要重置alpha.water的初始值,请将0/alpha.water文件复制到0/alpha.water:
?> cp 0/alpha.water 0/alpha.water
此时检查0/alpha.water字段的当前状态显示,整个内部字段的值均为0:
internalField uniform 0;
setFields实用程序可用于创建更复杂、不均匀的物理场分布。此实用程序由system/setFields字典控制。setFields应用程序的模板字典文件存储在应用程序源目录中:$FOAM_APP/utilities/pre-Processing/setFields。由于该文件相当长,因此不显示内容。然而,值得研究setFieldsDict的内容,因为它存储了setFields应用程序可用于预处理非均匀物理场的所有可用规范。
下面显示了测试用例的setFieldsDict的内容,以及用于初始化小水滴(即alpha.water值为1的圆)的添加的spherToCell子字典条目:
defaultFieldValues
(
volScalarFieldValue alpha.water 0
);
regions
(
boxToCell
{
box (0 0 -1) (0.1461 0.292 1);
fieldValues
(
volScalarFieldValue alpha.water 1
);
}
sphereToCell
{
origin (0.4 0.4 0);
radius 0.05;
fieldValues
(
volScalarFieldValue alpha.water 1
volVectorFieldValue U (-1 0 0)
);
}
);
初始场如下图所示。

defaultFieldValues将内部场设置为提供的默认值0,然后继续处理regions子字典。
setFieldsDict的语法对于上面所示的简单形状体积选择基本上是不言自明的。对于选定的体积,其单元中心位于该体积内的所有单元都将相应地设置给定的字段。例如,sphereToCell源选择中心位于指定中心和半径球体内的单元,并设置物理场alpha.water=1和U=(−1, 0, 0)。
为了预处理alpha.water并运行模拟,需要在命令行中执行以下步骤:
?> blockMesh
?> setFields
?> interFoam
图3.2显示了由于我们增加了setFieldDict而改变的初始条件的说明。
选择离散格式以及调整线性求解器的控制参数与选择边界条件同等重要。
离散格式在system/fvSchemes中定义,求解器由system/fvSolution字典控制。
3.3.1 数值格式(fvSchemes)
从用户的角度来看,与非结构化有限体积离散和插值相关的所有定义都在system/fvSchemes字典中定义。所需的设置因求解器而异,并取决于数学模型的特定项的公式。在有限体积法的框架内使用离散和插值格式来离散数学模型各项。
在OpenFOAM中,数学模型是使用区域指定语言(Domain Specific Language,DSL)在求解器应用程序中定义的。DSL作为抽象层发展起来,随着时间的推移,算法的实现也越来越高。在其他有关OpenFOAM的信息来源中,OpenFOAM DSL通常被称为公式模拟。在更高级别的抽象中使用算法和公式模拟,允许对数学模型进行非常可读的定义,以及对数学模型进行微不足道的修改。
例如,来自icoFoam求解器应用程序的以下源代码片段显示了动量守恒定律方程的OpenFOAM实现:
fvVectorMatrix UEqn
(
fvm::ddt(U)
+ fvm::div(phi, U)
- fvm::laplacian(nu, U)
);
solve(UEqn == -fvc::grad(p));
动量方程的不同项很容易识别、添加、删除或修改。对于这些项中的每一个,都需要在system/fvSchemes中定义等效的离散化。
注:区域指定语言(Domain Specific Language,DSL)是专门为某些应用程序开发的,它是软件开发的自然结果,具有明确的抽象层分离。根据离散化的方程、矩阵和源项而不是迭代循环、变量指针和函数进行思考,这代表了OpenFOAM中的方程模拟/DSL的基础。分离抽象级别是良好软件开发实践的标志。
离散和插值格式是上述源代码中列出的操作的组成部分,其将局部微分方程转化为代数方程,具有有限体积的平均性质。那些参与代数系统组装的项被称为隐式项(implicit terms),明确计算的项都被称为显式项(explicit terms)。显式项使用来自FVC(finite volume calculus)名称空间的离散运算符进行求值,而隐式项使用来自FVM(finite volume method)名称空间的运算符进行计算。记住这一区别很重要,因为在system/fvSchemes字典文件中为某项定义的离散格式将被用作应用程序代码中的fvc::和fvm::运算符的默认格式。
要获得特定项的支持格式列表,只需用任何单词替换fvSchemes字典文件中的现有格式并执行求解器。求解器返回的错误中会包括按目的选择的名称不存在格式。但是这之后是一个大列表,显示了所有可用的格式。为了获得关于格式参数(方案特定的关键字和值)的信息,用户需要浏览与格式实现相关的源文件。
在求解器应用程序中实现的方程式是在编译时定义的。但是,用于离散化这些方程项的格式的选择是在运行时执行的。这允许用户修改数学模型的离散方式:通过修改system/fvSchemes中的条目,为不同的问题选择不同的格式。
注:离散和插值是OpenFOAM中常用的算法。为了区分隐式算法(矩阵组装)和显式算法(源项),将算法利用C++命名空间进行分类。命名空间是一种编程语言结构,用于避免名称查找冲突(更多细节见[6])
cavityOscillating的system/fvSchemes字典为:
ddtSchemes
{
default Euler;
}
gradSchemes
{
default Gauss linear;
grad(p) Gauss linear;
}
divSchemes
{
default none;
div(phi,U) Gauss linear;
}
laplacianSchemes
{
default Gauss linear orthogonal;
}
interpolationSchemes
{
default linear;
}
snGradSchemes
{
default orthogonal;
}
每个fvSchemes字典都有相同的7个子字典,并且很可能在每个子字典的开头定义了一个默认参数。
将在icoFoam中实现的动量方程的代码片段与上面的清单进行比较,可以看出在此配置中,div(Phi,U)是使用线性方法离散化的。下面概述不同的离散化格式类别,以及所选格式的特点。
注:如果在第一次阅读后,对所选方案的以下描述不清楚,这并不会影响对本书其余部分的理解。感兴趣的读者可以稍后再阅读本书的这一部分,并与第一章一起阅读。在OpenFOAM中描述所有可用的格式超出了本书的范围,因此只讨论了几个选定的格式。
这些格式被分类为与数学模型项以及system/fvSchemes中的条目相关的类别:
- ddtSchemes
- gradSchemes
- divSchemes
- laplacianSchemes
- interpolationSchemes
- snGradSchemes
注:OpenFOAM中的所谓运行时选择(Run-Time Selection)允许在System/fvSchemes中选择不同的格式。如果system/fvSchemes中的条目错误,此模块将输出所有可用格式的列表。这可用于了解可用的格式:输入不存在的格式的名称会提供可用格式的列表。
3.3.1.1 ddtSchemes
ddtScheme是用于时间离散的格式。欧拉一阶时间(Euler first-order temporal)离散格式被设置为瞬态问题的默认值,其恰好是第一章中用来展示FVM离散实践的格式。时间离散化格式的备选方案包括:
- CoEuler
- CrankNicolson
- Euler
- SLTS
- backward
- bounded
- localEuler
- steadyState
在可用的时间离散化方案中,以下将更详细地解释CoEuler和backward。
1、CoEuler
CoEuler格式是一种一阶时间离散格式,既可用于隐式离散,也可用于显式离散。此格式可以自动调整局部时间步长,以便局部Courant数受用户指定的值限制。该格式使用当前时间步长值和从局部Courant数域计算的比例系数来计算局部时间步长。Courant数受限的局部时间步长的倒数计算为: 其中,局部面中心Courant数根据体积通量、面法向矢量及在面处连接的网格的网格中心之间的距离计算的: 在提供质量通量的情况下,需要利用密度场来计算局部面中心的Courant数: 其中为存储在面中心的质量通量。一旦计算出以面中心的Courant数,就可以使用公式(1)计算时间步长的倒数。对于面中心场,使用面中心的时间步长的倒数来计算一阶时间导数: 由于时间格式主要在网格中心场上操作,因此时间步长的倒数的网格中心值被计算为面中心的最大值,即 其被用来计算网格中心物理场的时间导数: 这样,使用时间步长δt倒数的局部计算场,局部计算时间导数。基于局部Courant数的时间导数的局部估计允许在Courant数较低的流域部分使用较大的时间步长。因此,模拟速度提高了(数值时间在计算域的这些部分人为地加快,因为那里的流动预计会经历较小的变化)。对局部Courant数进行限制,可以增强求解的数值稳定性。
2、backward
二阶后向格式或后向差分格式(BDS2)使用来自当前和两个连续的旧时间步长的物理量的值来组合二阶收敛时间导数。从当前时间开始,使用泰勒级数展开式计算导数,可追溯到两个时间步:
将方程(3.7)乘以4,然后减去方程(3.8),得到网格中心物理场的BDS2时间离散格式:
使用旧值计算导数是在OpenFOAM中完成的,不需要客户代码来存储旧的场和网格值。所有的体积场和面心场都有自动存储旧(o)和旧-旧(oo)时间步长值的能力。网格本身也能存储高阶时间离散化所需的信息(如旧的和旧-旧的网格体积场)。由于o和oo场值是已知的,backward格式计算的二阶时间导数可以被显式计算。实际实现时考虑到了时间步长的可能调整,得到以网格为中心的场的导数为: 式中,系数定义为:
而在两个次级时间步长相等的情况下,系数使用式(9)中的恒定时间步长进行离散化。
3.3.1.2 gradSchemes
梯度格式决定了对求解器中定义的项使用何种梯度计算方式。在实践中有许多例子表明,梯度格式的选择可能会得到更好的计算结果。例如,在两相流模拟中,梯度用于计算表面张力,因此它在由表面张力驱动的流动中起着重要作用。无论何时出现陡峭的梯度,或应用不同的网格拓扑(例如四面体网格),使用更广泛网格模板的梯度格式可能会提供更好的计算结果。
OpenFOAM中可用的梯度格式有:
- Gauss
- cellLimited
- cellMDLimited
- edgeCellsLeastSquares
- faceLimited
- faceMDLimited
- fourth
- leastSquares
- pointCellsLeastSquares
下面选择并描述了其中三种格式:Gauss、cellLimited和pointCellLeastSquares。
1、Gauss
Gauss格式是梯度项、散度项(对流项)和拉普拉斯项(扩散项)最常用的离散格式。第1章也对其进行了描述。此个需要以面心值来计算以体心值的梯度。
2、cellLimited
cellLimited格式扩展了标准梯度格式的功能,其为以网格体心的梯度值计算一个限制器,先以标准方式计算梯度,然后利用限制器对梯度值进行缩放。限制器通过网格体心属性值的最大值与最小值()来构造,该属性是通过间接搜索面相邻网格得到的,如下所示:
式中为网格中心的属性值;为网格的所有网格面相邻网格的集合。一旦得到网格面相邻网格的最小值和最大值,则使用最小值与最大值来计算其与网格体心值的差异:
差异值通过用户指定的系数() 进行缩放:
注意,当用户指定系数为1时,差异值不会进行缩放。
注:本节中的方程依赖于网格与网格之间的连接,它们也使用基于网格的模版。实际的实现是使用owner-neighbor寻址。
限制器初始值设置为1,但当其通过使用h在网格面上循环计算时,其值会被更新。这也是为什么min和max函数将给定的最小值和最大值的属性差与梯度给出的外推差的比率进行比较的原因: 这里为连接网格体心与网格面中心的向量。之后使用与min/max的值相比增加的差值来计算限制器: 用限制器缩放标准方式计算得到的梯度来确定网格中心点的最终梯度值: 3、pointCellsLeastSquares
PointCellsLastSquares为梯度提供了更大的模板,其引入相邻的网格单元,这些网格与所讨论的网格相邻,不仅跨网格面,而且跨网格节点。在非结构化六面体网格上,此模板包含个网格。虽然在OpenFOAM中实现的数值格式是二阶收敛的,但当流场中出现急剧阶跃时,绝对精度成为数值近似的另一个非常重要的方面。使用更宽的模板,该格式提供了梯度估计,且绝对误差较低。若对网格中心的属性进行线性泰勒展开,可以得到: 计算三个未知变量(梯度的三个分量)需要三个值。最小二乘梯度涉及将泰勒级数(方程式3.23)从计算梯度的网格中心扩展到相邻网格。展开次数与网格模板的大小成正比。对于二维三角形网格,可以直接从相邻模板的周围三个网格计算梯度。但是,在模板中包含更多的网格可以提高梯度的绝对精度。当已知三个以上的点值时,系统会变得过渡确定。因此,使用最小平方梯度误差计算梯度,定义为: 其中是模板的网格。是与所讨论的网格和模板网格相关的加权因子。通常将两个网格之间的反向距离作为权重,是从计算梯度的网格到模板网格的泰勒展开的平方误差: 经过一些代数处理([4]),使平方误差最小化,得到梯度分量的线性代数系统。由于系统尺寸为3×3,因此对每个单元的线性代数系统尺寸进行组装和求解。此外,由于系数矩阵是对称张量,因此通过直接反转每个网格的系数矩阵来获得解。作为使用此梯度方案的动机,考虑图3.3,其中体积分数场的梯度是使用标准Gauss linear和新的PointCellsLastSquares梯度格式计算的。体积分数场设置为半径R=2cm的圆,中心位于6×6 cm的区域内,使用具有30×30体积的网格进行离散化([1])。PointCellsLastSquares计算圆形液滴的梯度比Gauss linear计算得到的更均匀,因为梯度计算中涉及到点邻域。点邻域的参与提高了具有急剧阶跃的场的绝对精度。
提示:图3.3中示例字段所示的高斯梯度计算是网格各向异性的教科书示例-计算强烈依赖于面相对于坐标轴的方向。
提示:作为练习,尝试计算不同网格上陡峭显式函数的梯度,并比较不同梯度格式的误差收敛性。
3.3.1.3 divSchemes
divScheme用于离散数学模型中的对流(散度)项。散度项最常使用的空间离散格式是Gauss离散格式,其使用高斯散度定理。离散格式是FVM的基础,因为它生成了一个代数方程组,这使得不太可能在配置文件中更改隐式项。此外,可为涉及稳态或部分收敛解的模拟提供有界选项,其中在求求解法的迭代过程中不完全满足。在这种情况下,从系数矩阵中扣除以提高计算收敛性。
3.3.1.4 laplacianSchemes
system/fvSchemes字典中的laplacianSchemes子字典由Gauss离散和interpolation格式组合而成。Gauss离散是扩散(拉普拉斯)项离散的基本选择,用户可以选择interpolation格式。
3.3.1.5 interpolationSchemes
interpolationSchemes修改面心值的插值方式。不同的插值格式可与空间离散格式一起选择,例如Gauss离散格式。另一方面,可以使用更大的点-值对集合对面上的值进行插值,从而提高插值的精度,然后将使用Gauss离散格式使用面插值来离散散度项、拉普拉斯项或梯度项。
OpenFOAM在interpolation格式方面提供了多种选择:biLinearFit、blended、clippedLinear、CoBlended、cubic、cubicUpwindFit、downwind等。大多数可用的插值格式用于离散对流项。应用特定的数值格式会在对流项中引入不同的数值误差,尤其是当对流特性在解域中发生阶跃时。例如众所周知中心差分格式(CDS,线性)会在解中引入数值不稳定性,而迎风差分格式(UDS,迎风)会人为地平滑对流场([2],[7])。因此,开发了不同的数值格式来抵消原始格式的负面影响,要么涉及高阶插值,要么将最终插值计算为其他插值方案获得的值的组合。
3.3.2 求解控制(fvSolution)
数学模型的离散构造了形为的代数方程组。该系统可以使用直接法或迭代方法来完成。正如[2]所指出的,当求解大型稀疏矩阵时,直接方法的计算成本非常高。与此类矩阵方程的求解过程相关的所有设置,以及压力-速度耦合都在system/fvSolution中完成。根据使用的求解器,该文件的内容会有所不同。
对于前面使用icoFoam求解器的cavity案例,其fvSolution字典的预设定义为:
solvers
{
p
{
solver PCG;
preconditioner DIC;
tolerance 1e-06;
relTol 0.0;
}
U
{
solver PBiCG;
preconditioner DILU;
tolerance 1e-05;
relTol 0;
}
}
PISO
{
nCorrectors 2;
nNonOrthogonalCorrectors 0;
pRefCell 0;
pRefValue 0;
}
此字典文件中共包含两个子字典:solver与PISO。所有求解器都需要包含solver子字典,因为其包含所使用的各种矩阵求解器的选项和参数。将矩阵求解器与实现特定数学模型的求解器应用程序区分开来很重要。第二个字典存储PISO压力-速度耦合算法所需的参数。OpenFOAM中还有其他压力-速度耦合算法,如SIMPLE和PIMPLE。它们中的每一个都需要在fvSolution中提供一个具有特定算法名称的字典。
提示:OpenFOAM中有两种类型的求解器:solver应用程序和线性求解器。solver应用程序是最终用户直接用于运行仿真的程序。线性求解器是用于求解线性代数方程组的算法,是模拟求解过程的一部分。通常,求解器应用程序简称为solver,因此从现在起,此术语用于求解器应用程序。
3.3.2.1 Linear Solver
上述示例使用PCG求解压力方程,并使用DIC对矩阵进行预处理,DIC可用于对称矩阵。另一方面,对于动量方程,使用非对称PBiCG求解器和DILU预处理器。
无论矩阵求解器是什么,都可以定义以下参数:
tolerance。定义求解器的退出标准。这意味着,如果从一个迭代到下一个迭代的变化低于该阈值,则认为求解过程充分收敛并停止。例如,在对稳态问题进行稳态模拟时,容差应非常小,以提高收敛性和准确性。另一方面,对于瞬态问题,无法获得稳态解,因此容差不能选择得非常小。
relTol。将相对容差定义为求解器的推出标准。若将此参数设置为非零值,则会覆盖tolerance设置。tolerance定义了两次迭代之间的绝对变化,而relTol定义了相对变化。值0.01将强制求解器在两次连续迭代之间迭代知道达到100%的变化。当模拟强非稳态问题且容差设置导致高迭代次数时,使用此参数较为方便。
maxIter。一个可选参数,其默认值为1000。定义了迭代的最大次数,直到求解器停止为止。
3.3.2.1 压力-速度耦合
根据所选的求解器应用程序,将在相应的求解器中实现不同的压力-速度耦合算法。求解器应用程序尝试读取fvSolution中的子字典,具体取决于实现的压力-速度耦合算法。
提示:有关各种算法的更多背景信息,请参阅[2,7]。OpenFOAM wiki上也有大量可用信息。
无论如何都必须定义一些参数:
nNonOrthogonalCorrectors:此参数定义了许多内部循环,用于校正网格的非正交性。当使用四面体网格或在六面体网格上应用局部动态自适应网格细化时,此参数是必需的。[3]和[2]详细描述了非正交性对方程离散化的影响。由于校正是显式的,所以引入了内部循环。它需要多次应用,因为每个应用程序都会减少错误,并且不会完全消除错误。
pRefPoint/pRefCell:这些选项中的任何一个都定义了假定参考压力的位置。pRefPoint采用网格坐标系中的向量,而pRefCell仅采用压力所在网格的标签。对于多相流,该点应始终由任一相覆盖,且不在其间变化。仅当压力未通过任何边界条件固定时,才需要这些参数。
pRefValue:定义参考压力值,通常为零。
特定压力-速度耦合算法或求解器可能需要其他参数。求解器越复杂,fvSolution中通常需要的选项就越多。求解器教程通常提供足够的信息来运行案例。
执行求解器就像在Linux下发出任何其他命令一样简单:只需键入命令名并按enter键。一般来说,求解器和任何其他OpenFOAM应用程序都应该在case目录中执行。从其他目录执行求解器需要将-case参数传递给求解器,其后接案例的路径。对于使用icoFoam求解器模拟的cavity案例,命令如下所示:
icoFoam
根据网格大小、时间步长和要模拟的总时间,与通常的ls或cp命令一样,此命令确实需要更长的时间。此外,输出到终端的信息量很大,一旦终端关闭就会丢失。因此,应扩展执行求解器的语法:
nohup icoFoam > log &
tail -f log
nohup命令指示shell保持作业运行,即使在shell窗口关闭或用户注销时也是如此。不是将所有内容都打印到屏幕上,而是将输出通过管道传输到名为log的文件中,然后将作业移到后台。由于作业在后台运行,并且所有输出都转发到日志文件,因此tail命令用于将文件结尾打印到屏幕上。通过将-f作为参数传递,这将一直更新,直到用户退出命令为止。另一个与正在运行的作业保持同步的选项是使用pyFoamPlotWatcher,其解析日志文件并从中生成gnuplot窗口。这些窗口会自动更新,并包含残差图,这便于监控模拟。
与在后台手动启动求解器并将输出重定向到日志文件不同,还可以使用foamJob脚本:
foamJob icoFoam
foamJob脚本非常强大,因为它为启动OpenFOAM作业提供了一个多功能一体的解决方案。下一节将介绍foamJob的一些特性。
3.4.1 controlDict配置
每个case都必须包含一个system/controlDict文件,该文件定义了所有与运行时相关的数据。包括停止求解器的时间、时间步长、时间步长数据写入间隔和方法。此字典的内容在求解器运行时自动重新读取,因此允许在模拟运行时进行更改。
OpenFOAM用户指南[5]全面介绍了参数和参数组合,因此此处不再重复此信息。这两个参数在这里有更详细的解释,正如本书其余部分所述。
writeControl:writeControl表示数据写入磁盘的时间。可以选择timeStep、runTime或adjustableRunTime。实际间隔由writeInterval定义,它只接受标量值。为了简单起见,从现在起这个间隔被命名为n。如果选择了timeStep,则每n个时间步都会写入磁盘,而选择runTime则每n秒写入case目录。最后一个常用的选项是adjustableRunTime,它每n秒向磁盘写入一次,但会调整时间步长,以使此间隔完全匹配。因此,case文件夹中只会出现名称很好的时间目录。使用默认设置,写入磁盘的数据量不受OpenFOAM的限制。特别是在许多用户访问同一存储单元并且运行时间较长的情况下,这可能会很快填满磁盘。
purgeWrite:purgeWrite可以通过使用过多的存储来避免上述问题。默认情况下此参数设置为0,并且不限制case写入磁盘的时间量。将其更改为2将指示OpenFOAM仅在磁盘上保留最新的2个时间实例,并在每次数据写入磁盘时删除其他实例。此选项不能用于将writeControl设置为adjustableRunTime的情况。
除了这些标准参数外,controlDict还包含在运行时链接到解算器的自定义库以及对函数对象的调用。
3.4.2 分解和并行执行
到目前为止,所有解算器都在单个处理器上执行。CFD算法的结构使其能够实现数据并行:计算域被划分为多个部分,相同的任务在计算域的每个部分上并行执行。每个进程与其邻居通信并共享相关数据。在现代多核体系结构和HPC集群中,将工作负载分布在多个计算单元上通常会导致执行时间加快。计算区域的分解决不能影响方法的数值性质:一致性、有界性、稳定性和守恒性。
在OpenFOAM中,数据并行是以一种非常优雅的方式实现的,它与底层FVM密切相关。实际上,第1章中用于阐述方程离散化的边界面也可能是处理器(进程)边界的面。在并行执行模拟之前,必须将计算域划分为与用于模拟的进程数量相同的子域。
提示:在单处理器内核上执行解算器通常被称为“串行执行”。
作为并行执行的一个示例,icoFoam解算器的cavity案例分布在开始作业的机器的两个核心上。必须确认机器至少有2个内核,否则模拟将比串行运行花费更长的时间。为了利用这两个核心,数据必须分布在它们之间。
提示:OpenFOAM中非结构化网格上的进程间通信(IPC)和FVM之间的交互由离散微分算子自动处理,其细节相对复杂,超出了本书的范围。
$FOAM_RUN文件夹可用于在$HOME文件夹中运行OpenFOAM仿真,但需要先创建它。
mkdir -p $FOAM_RUN
若要在$FOAM_RUN中运行算例,可以先拷贝cavity算例到路径下:
cp -r $FOAM_TUTORIALS/incompressible/icoFoam/cavity/cavity $FOAM_RUN/
cd $FOAM_RUN/cavity
在下一步中,选择计算域的分解方式。OpenFOAM中存在各种分解域的方法。本教程使用scotch区域分解。域分解配置存储在字典文件system/decomposeParDict中。用户可以在OpenFOAM教程中使用下面的命令搜索此文件:
find $FOAM_TUTORIALS -type -iname decomposeParDict
默认情况下,cavity教程案例不包含此文件。只需将OpenFOAM教程中某个地方的任何decomposeParDict复制到当前目录下即可。
cp $FOAM_TUTORIALS/multiphase/interFoam/laminar/damBreak/damBreak/system/decomposeParDict ./system
decomposeParDict最重要的行如下:
numberOfSubdomains 4;
method simple;
第一行定义将使用多少子域(或MPI进程),第二行选择应用于分解域的方法。对于实际应用程序来说,使用simple方法通常是一个不好的选择,因为它将域分割为空间相等的部分。这样做不会最小化子域之间进程间通信边界的大小。考虑到网格一侧非常密集,另一侧非常粗糙,简单方法会将其切成两半,生成有限体积分布非常不均匀的子域。具有更多有限体积的网格需要更多的计算资源,使得模拟不平衡。不必要的大进程间通信边界导致进程间通信时间增加,这会严重降低并行执行的效率。
为了优化这一点,存在各种自动分解方法,例如:优化处理器边界,以使进程间通信开销最小化。通过如下更改system/DecomposePartict中的行,可以确保将域分解为两个子域,并使用scotch方法:
numberOfSubdomains 2;
method scotch;
在分解域之前须生成网格。此示例使用基于blockMesh的网格。生成网格后,必须使用decomposePar执行域分解:
blockMesh
decomposePar
案例目录中生成了两个新目录:processor0和processor1。其中每个都包含一个子域,包括网格(位于processor*/polyMesh目录中)和字段(位于processor*/0目录中)。并行启动模拟的实际命令比串行命令长一点,因为需要使用MPI:
mpirun -np 2 icoFoam -parallel > log
这将调用带有2个子进程的mpirun来并行运行icoFoam,并将输出存储在日志中以供以后评估。mpirun的-parallel参数非常重要,因为它指示mpirun使用其特定子域运行每个进程。如果缺少此参数,将启动2个进程,但这两个进程都使用整个域,这不仅是冗余的,而且也是计算能力的浪费。
当模拟完成后,子域可以重建为一个单独的域。为此使用reconstructPar工具,默认情况下,该工具从每个处理器目录中获取所有时间实例并对其进行重建。当使用可选参数latestTime调用reconstructPar时,只能选择最后一个时间步骤。它指示reconstructPar仅重建最近的时间。当网格非常大并且重建需要大量时间和磁盘空间时,这很方便。无需重建子流程域,因为ParaView可以可视化分解的OpenFOAM案例。
虽然人们可能会观察到执行时间随着使用的处理器数量的增加而有很好的伸缩性,但低于某个总单元与子域的比率通常是个坏主意。进程本身会变慢,瓶颈不是可用的处理器能力,而是进程之间的通信。并行执行模拟结果,加速比s如下所示 其中和分别是串行和并行执行时间。线性(理想)加速比等于使用的进程数。通常,由于进程间通信或子域局部的瓶颈(前面提到的局部计算),加速比的值将小于进程数。对于涉及更大网格算例的模拟,和评估的之间的差异将更大。然而,可能会出现超线性加速,其中:背后的原因通常特定于执行模拟的算法和架构。
在本章中,我们将CFD工作流的下一步带入案例设置和模拟运行阶段。这需要为模拟中涉及的物理场设置初始值和边界值,这可以通过各种实用程序完成。离散和插值格式是OpenFOAM中有限体积法的关键组成部分,用户可以在开始时或在模拟过程中选择。
在OpenFOAM中,有许多插值和离散格式可用,因此我们只提到其中的几个。如果配置文件中提供了错误条目,OpenFOAM将报告所有可用格式的列表。我们浏览了一些格式的数字基础,它们干净的软件设计允许感兴趣的读者在不深入了解C++编程语言的情况下了解格式的工作原理。最后,我们展示了用户如何在串行和并行模式下执行求解器。
- J. U. Brackbill, D. B. Kothe, and C. Zemach. “A continuum method for modeling surface tension”. In: J. Comput. Phys. 100.2 (June 1992), pp. 335–354. Issn: 0021-9991.
- J. H. Ferziger and M. Perić. Computational Methods for Fluid Dynamics. 3 rd rev. Ed. Berlin: Springer, 2002.
- Jasak. “Error Analysis and Estimatino for the Finite Volume Method with Applications to Fluid Flows”. PhD thesis. Imperial College of Science, 1996.
- Dimitri J. Mavriplis. Revisiting the Least-squares Procedure for Gradient Reconstruction on Unstructured Meshes. Tech. Rep. National Institute of Aerospace, Hampton, Virginia, 2003.
- OpenFOAM User Guide. OpenCFD limited. 2016.
- Bjarne Stroustrup. The C++ Programming Language. 3 rd. Boston, MA, USA: Addison-Wesley Longman Publishing Co., Inc., 2000.
- H. K. Versteeg and W. Malalasekra. An Introduction to Compu- tational Fluid Dynamics: The Finite Volume Method Approach. Prentice Hall, 1996.
本章介绍后处理、可视化和数据采样的基础知识。不仅讨论 OpenFOAM 工具,还讨论用于各种任务的 paraView 以及运行时数据采样。
4.1 后处理
CFD 分析的后处理步骤是从计算的 CFD 结果中提取有用信息的任务。提取的数据可以采用图像、动画、绘图、统计等形式。值得庆幸的是,OpenFOAM 配备了大量的后处理工具,可以满足大多数用户的需求。这些工具以所谓的函数对象的形式出现,可以在模拟完成后调用,或者在模拟作为一种辅助计算在运行时调用。例如,如果需要涡量场但默认情况下不由求解器计算,则可以将涡量函数对象添加到模拟中,以便将其与预期的压力和速度场一起计算和写入。函数对象和设计将在第 12 章进行深入回顾。库存后处理工具(也称为函数对象)的源代码存储在$FOAM_SRC/functionObjects目录下的各种分类子目录中:
ls $FOAM_SRC/functionObjects
field graphics lagrangian solvers
forces initialisation randomProcesses utilities
虽然某些后处理计算可能无法使用现有实用程序直接计算,但使用库存实用程序的计算组合可能会完成工作。与其他 OpenFOAM 实用程序类似,后处理应用程序默认在模拟案例中的所有现有时间目录上运行。可以通过传递 -time 参数显式选择时间和时间范围,并且可以通过-latestTime参数选择上次时间。在详细介绍示例工作流场景之前,下面将介绍一些现有的后处理工具。虽然描述所有这些超出了本书的范围,但涵盖了一些对许多用户应该有价值的选定应用程序。
4.1.1 postProcess
第一个选择的工具是通用的 -postProcess 求解器选项,其可用于对现有流场执行各种计算。所有计算结果都存储为相应时间目录中的新的未来城。此求解器选项增强了求解器的行为,其不执行流动计算,而仅执行命令行中包含的函数对象或在 controlDict 中设置的函数对象。此选项附加到求解器,以确保在后处理之前加载与特定求解器关联的物理场和模型。一般语法是:
solverName -postProcess -field <field name> -func <function name>
其中 solverName 是最初用于计算现有流动数据的求解器的名称。
在上面的语法中,<function name> 定义要执行的计算类型,<field name> 表示要操作的物理场,<arguments> 提供操作特定的控件。请注意,并非所有函数对象都需要输入物理场名称。大多数 OpenFOAM 实用程序中常见的附加参数,例如 -latestTime 和 -case 也可以与该实用程序一起使用。对流场结果本身进行的所有现有计算都可以在这里找到:
$FOAM_SRC/functionObjects/field
下面概述了一些更常用的算术或场微积分运算:
components。将矢量或张量场的分量分离为单独的体积标量场。例如,可以使用以下语法将速度场 U 分成三个volScalarField(Ux、Uy 和 Uz):
simpleFoam -postProcess -func 'components(U)'
div。计算向量场或张量场的散度,并将结果分别写入新的标量场或向量场。 fvSchemes 字典中必须存在散度运算符的数值格式(例如 div(U))才能执行。如速度场 U 的散度可以通过下式计算
simpleFoam -postProcess -func 'div(U)'
将计算结果存储为一个名为 divU 的新 volScalarField,存放在特定的时间步长目录中。
mag。用于计算物理场场的大小。对于标量值,计算其绝对值,对于矢量值,计算其幅值。结果存储在一个新的物理场中,该物理场由带有前置 mag 的旧字段名称组成。例如,计算速度场 U 的速度大小可以通过执行以下操作来实现:
simpleFoam -postProcess -func 'mag(U)'
magSqr。分别计算场的幅值平方。将计算结果写入一个新的标量场中,该标量场根据模式“magSqr”命名,后跟原始场的名称。
simpleFoam -postProcess -func 'magSqr(U)'
4.1.2 yPlus
对于采用湍流建模的模拟,y+ 值是一个重要值,用于验证近壁流是否得到充分解析,以及该分辨率是否在该湍流模型的正确范围内。更多关于这个值的含义和计算方法的信息可以从第 7 章查看。y+ 后处理工具的源代码位于此处:
ls $FOAM_SRC/functionObjects/field/yPlus
y+ 值是在模拟完成后使用 yPlus 函数对象计算的。以前版本的代码需要调用不同的实用程序,具体取决于仿真是采用 LES 还是 RANS 类型的模型,但最近已将这两种仿真类型统一到单个进程中。 y+ 值存储在一个名为 yPlus 的新 volScalarField 中:
simpleFoam -postProcess -func yPlus
在上面的示例中,simpleFoam 被称为基础求解器。在一般情况下,任何用于计算流场的流动求解器都可以替换,例如用于瞬态流动的 pisoFoam。 y+ 场仅在边界面上计算,边界面为壁面类型,剩余的以单元为中心的值为零。除了新写的物理场外,这两个 yPlus 工具都会在屏幕上打印一些有价值的信息。此信息包含用于特定湍流模型的系数以及所有壁边界补丁的最小、最大和平均 y+ 值。
4.1.3 边界平均与边界积分
这些后处理工具可用于分别计算边界的平均值和积分。这两个工具的源代码都位于 postProcessing 实用程序的 patch 子目录中。
ls $FOAM_UTILITIES/postProcessing/patch
- patchAverage。计算由面法向向量的大小进行加权的标量的算数平均值:
- patchIntegrate。计算边界上物理场的积分值。对于该计算,采用了两种不同的方法: 使用面积法向量 及其幅值。两个结果都输出到控制台,分别产生一个矢量和一个标量结果。
patchAverage 只能处理 volScalarField,而 patchIntegrate 还将处理 surfaceScalarField 作为输入。从命令行调用时,这两个命令都需要相同的参数集:
postProcess -func 'patchAverage(<fieldName> ,name=<patch> )'
postProcess -func 'patchIntegrate(<fieldName> ,name=<patch> '
在上面的代码片段中,<field> 和 <patch> 分别代表要操作的物理场和边界。结果不会存储在案例目录中的任何位置,而只会输出到终端。不过可以通过将特定实用程序的输出通过管道传输到日志文件来存储它们。下面显示的是在现有物理场和管道到存储的文本文件的案例上进行这些计算的示例。
postProcess -func 'patchAverage(<fieldName> ,name=<patch> )' > patchAveResults.txt
postProcess -func 'patchIntegrate(<fieldName> ,name=<patch> )' > patchIntegrateResult.txt
4.1.4 vorticity
vorticity 实用程序使用速度场 U 计算涡量场 ω,并将结果写入名为 vorticity 的 volVectorField。速度场的涡度表示流动中的局部大小和旋转方向,并在方程 4.2 中定义。执行此操作也称为获取物理场的旋度。该实用程序的最终输出是写入每个时间目录的计算涡度场。
此后处理实用程序的源代码可以在 $FOAM_UTILITIES/postProcessing/velocityField/vorticity 中找到,可以采用下面的命令执行:
postProcess -func vorticity
4.1.5 probeLocation
如果在后处理期间需要在某些位置探测现场数据,则 probeLocations 是首选工具。此工具需要输入字典,可以在 system/probesDict 中设置,也可以作为 system/controlDict 中的函数对象调用。它围绕两个列表进行操作,一个包含要探测的字段的名称,另一个包含要从中探测字段值的空间位置。一般来说,如果计算后只需要探测解,使用probesDict是合适的。如果需要在模拟运行时(例如在瞬态模拟的实例中)写入瞬态探测数据,请将探测过程作为函数对象添加到 controlDict。要在 [0, 0, 0] 和 [1, 1, 1] 两个点处对压力场 p 和速度场 U 进行采样,probesDict 的配置如下所示:
fields(P U);
probeLocations
(
(0 0 0)
(1 1 1)
);
如果没有另外说明,则在所有现有时间对物理场进行探测,输出文件位于案例目录内的嵌套子目录中。第一个文件夹被命名为probes,子文件夹表示数据采样的第一个时间步。例如,探测收集的所有压力数据都可以在文件 probes/0/p 中找到。数据以表格方式排列,时间存储在第一列,然后是提取的物理场的值。然后可以使用 gnuplot 或 python/matplotlib 等绘图实用程序处理此格式。下面显示了压力场探测结果的示例。
# x 0 1
# y 0 1
# z 0 1
# Time
0 0 0
10 3.2323 2.2242
4.1.6 案例示例
作为展示后处理工具可能应用的示例,我们选择了二维 NACA0012 水翼。水翼被深度淹没并放置在具有均匀流入的区域中。得到的雷诺数为 Re = 1e6。NACA 剖面的弦长为 c = 1m,运动粘度为 ν = 1e−6 m2 s,这给出了自由流速度为 v = 1m/s。
该案例可以在chapter4/naca下的存储库中找到,并且应该复制到用户目录中:
run
cp -r chapter4/naca .
cd naca
要生成结果,必须执行教程随附的 Allrun 脚本。模拟完成后,检查 NACA 表面上的 y+ 分布。为此,必须在案例目录中执行 yPlus 后处理函数对象,并且必须使用 paraView 在表面上可视化生成的 yPlus场。
尽管 yPlus 将最小、最大和平均 y+ 值打印到屏幕上,但可以根据 yPlus 场以不同的方式重新计算平均值。在计算了初始 yPlus 场之后,使用 patchAverage 正是这样做的:
./Allrun
simpleFoam -postProcess -func yPlus
postProcess -func 'patchAverage(yPlus,name=FOIL)'
输出的结果不利于图形绘制,因为存在一些输出开销和多余的文本元素。通过使用 grep 仅查找行尾的浮点数,可以从 patchAverage 函数输出中过滤掉平均值。对于以后的处理,可以将它们通过管道传输到文本文件 yPlusAverage。这可以通过运行如下所示的命令来执行:
postProcess -func 'patchAverage(yPlus,name=FOIL)' | grep -o -E '[0-9]*\.[0-9]+$' > yPlusAverage.dat
另一个实际的后处理任务是计算 x 方向上的积分和平均壁面剪应力。剪应力本身可以通过 wallShearStress 计算,它将一个新的 volVectorField 写入每个时间步目录。通过简单地链接各个命令,可以计算平均 wallShearStress,而不需要使用 paraView:
simpleFoam -postProcess -func wallShearStress
postProcess -func 'component(wallShearStress)'
postProcess -func 'patchAverage(wallShearStressx,name=FOIL)' | grep -o -E '(-|+)?[0-9]*\.[0-9]+$' > stressXAverage.dat
后处理方法示例提供了一种易于使用且功能强大的方法来提取模拟数据。虽然有许多可视化应用程序可以产生有吸引力的图像,但样本更适合视觉上不那么吸引人但可以说更重要的定量分析角色。例如,不是从速度赋值表示中直观地估计边界层厚度,而是可以从原始或插值速度数据中提取它并放入数据表中。
通常,采样用于提取和生成模拟结果的数据子集的 1D、2D 或 3D 表示,例如点值、线图或等值面。支持不同的输出格式,以及不同的几何采样实体。
在以前的 OpenFOAM 版本中,sample 是一个独立的实用程序,但后来被弃用,现在其分布在各种后处理函数对象之间。这种较新的配置允许在模拟运行期间以及模拟完成后执行所有采样操作。这些函数现在通常在默认情况下通过函数子字典中的 controlDict 定义。或者,只要用户在调用后处理实用程序时指向适当的文件,就可以在单独的字典中定义函数。后一种方法倾向于帮助案件和后处理程序保持条理,将在下面概述。此处的示例案例字典中概述了各种点探针、图形或表面提取功能配置的示例:
?> ls $FOAM_ETC/caseDicts/postProcessing/probes
boundaryCloud cloud.cfg internalCloud.cfg probes.cfg
boundaryCloud.cfg internalCloud probes
?> ls $FOAM_ETC/caseDicts/postProcessing/graphs
graph.cfg sampleDict.cfg singleGraph
?> ls $FOAM_ETC/caseDicts/postProcessing/visulaization
runTimePostPro.cfg streamlines streamlines.cfg surfaces surfaces.cfg
在文本编辑器中从etc打开上面所示的示例,将显示示例后处理实用程序的所有可用配置选项。 有大量可用的选项,并且提供的采样文档非常详细。 这些选项以清晰的方式进行了描述。 sample可以处理大量的采样参数:字段名、输出格式、网格集合、插值方案和曲面。
无论采样参数如何变化,sample 始终以相同的方式处理数据采样过程,而不管用户选择的参数子集如何。通过在物理场单词列表中提供场名称来选择要采样的字段。网格的子集(集合子字典)或几何实体(表面子字典)用于定位数据采样点。如果数据采样点与保存现场数据的网格点(例如像元中心或面中心)不一致,则使用不同的插值方案(interpolationScheme 参数)对数据进行插值。然后将插值数据以指定的输出格式(setFormat 参数)存储在案例中。
一维数据提取的一个例子是定义一条与流动域相交的线,并沿这条线对速度场进行采样。这可用于采样,例如速度分布。然后可以使用任何首选的绘图实用程序将此提取的配置文件与其他数据集进行比较。
sample 的另一个示例应用是在大型模拟案例中提取边界场值。无需尝试在 paraView 中打开整个模拟案例,可以使用 sample 仅提取相关边界上的值。这种使用样本进行后处理的本地化方法可以大大减少所需的计算资源,具体取决于数据集的大小。
任何模拟案例都可用于展示如何使用示例实用程序对模拟数据进行采样。为此,选择了二维上升气泡测试用例,可在示例用例存储库的 chapter4/risingBubble2D 子目录中找到。为了在这种情况下成功使用样本,必须执行模拟:
blockMesh
setField
interFoam
接下来的部分涵盖了使用示例的示例,它们都涉及操作函数子字典。虽然此子字典可以在 controlDict 中定义,但它也可以在单独的自定义字典文件中定义,这是我们将在本示例中使用的方法。
注:在继续执行示例之前,请在选择的文本编辑器中打开随示例源代码提供的 sampleDict,以查看所有可能的采样配置选项。
4.2.1 沿直线采样
在此示例中(上升气泡),在 2D 气泡位于模拟域的顶部壁面后检查其宽度。采样线将在时间 t = 7.0 s 沿穿过气泡的线对 alpha.liquid 场进线采样。配置为沿线采样的函数子字典如下所示:
setFormat raw;
interpolationScheme cellPoint;
fields
(
alpha.liquid
p_rgh
U
);
sets
(
alphaWaterLine
{
type uniform;
axis distance;
start (-0.001 1.88 0.005);
end (2.01 1.88 0.005);
nPoints 250;
}
);
setFormat选项更改写入文件的数据的格式,interpolationScheme选项指定在将数据映射到示例线之前发生的值插值类型(如果有)。 所有要采样的字段都需要在字段列表中列出-在本例中是alpha.water字段。 sets子字典包含提取的所有示例线的列表。
alphaWaterline子字典的类型条目定义了采样数据如何沿直线分布--在本例中,使用均匀点分布。 Axis参数确定如何写入点坐标-距离导致参数化输出,因为坐标是从第一个直线点开始的沿直线的距离。 Axis参数还有其他可用的选项,例如XYZ,其中采样点的绝对位置向量将被写入数据文件的第一列。 接下来,对于线条样本,需要提供三维起点和终点。 在此设置中,npoints指定采样点的数量。
注意:将取样线稍微调整到远离边界的位置。通常,取样线不与网格面共面,因为这样无法确定与采样线相交的网格。
一旦配置了sampledict.set,就可以执行以下命令对t=7 s执行postprocess:
interFoam -postProcess -dict ./system/sampleDict.set -time 0.7
此命令将创建一个新目录,其中包含以下文件:
?> ls postProcessing/sets/7
alphaWaterLine_alphaWater_p.xy alphaWaterLine_U.xy
标量场alpha.water和p存储在同一个文件中,而采样的矢量速度场存储在单独的文件中。 alpha.water场值可以从存储的数据中可视化,使用绘图工具,应该会导致类似于图4.2的图。
注:如果在执行sample时省略-time7选项,则会对每个timeStep进行采样,从而对相应的XY数据进行插值和保存。
4.2.2 在平面上采样
沿平面采样对于大型3D案例特别有用,这些案例可能非常大,需要很长时间才能通过网络连接传输模拟数据。为平面设置采样的过程与设置线采样非常相似。需要配置surfaceFormat条目,并且需要在surfaces子字典内部提供样本平面列表。与线采样类似,应避免使采样平面与网格面共面。
先前的interpolationScheme集合再次用于将以单元为中心的流动数据插值到平面上。这种设置的示例sampleDict如下所示:
functions
{
surfaces
{
type surfaces;
surfaceFormat vtk;
writeControl writeTime;
interpolationScheme cellPoint;
fields (U p_rgh alpha.water);
surfaces
(
constantPlane
(
type cuttingPlane;
planeType pointAndNormal;
pointAndNormalDict
{
point (1.0 1.0 0.005);
normal (0.0 0.0 1.0);
}
)
);
};
}
为面选择VTK输出格式,并且在constantPlane子目录中将曲面类型设置为Plane。 使用点位置向量(point)和平面法向量(normal)定义平面。
为了生成visualization toolkit(visualization toolkit,VTK)平面曲面并提取alpha.water数据,-postprocess在Chapter4/RisingBubble2D案例的特定显式时间目录上执行:
interFoam -postProcess -dict ./system/sample.surface -time 7
在PostProcessing文件夹中创建了一个surfaces/7子目录,其中包含采样数据:
> ls postProcessing/surfaces/7
constantPlane.vtp
显然,随着物理场的采样,存储了尽可能多的VTK面。可以直接在paraView中打开以VTK格式存储的面来可视化。在图4.3中,用采样的alpha.water场示出采样的平面。由于risingBubble2D情况是二维的,因此该采样示例的结果与在paraView中使用剪切过滤器时的结果相同。

4.2.3 等值面生成与插值
除了提取数据外,-postprocess实用程序还可以从现有的流动数据中生成等值面。 在这个例子中,它被用来生成一个表示气液界面的等值面,并在其上插值压力场。 等值面类型配置在sampleDict的Surfaces子字典中:
functions
{
// Surfaces sample function object
surfaces
{
type surfaces;
surfaceFormat vtk;
writeControl writeTime;
interpolationScheme cellPoint;
fields (U p_rgh alpha.water);
surfaces
(
fluidInterface
(
type
isoSurface;
isoField alpha.water;
isoValue 0.5;
interpolate true;
pointAndNormalDict
{
point (1.0 1.0 0.005);
normal (0.0 0.0 1.0);
}
)
);
};
}
为了生成等值面,-postprocess将在t=7s输出求解上执行:
interFoam -postProcess -dict ./system/sample.isoSurface -time 7
在图4.4中显示了 alpha.water = 0.5的等表面,其中相互作用的压力作用在气泡上。
4.2.4 边界采样
-postprocess的功能并不局限于创建样本平面和样本线。 可以提取整个patch,并将任何所需的边界流场值映射到patch上。 尽管使用了一个相当小的二维模拟案例来说明这一过程,但补丁采样更适合于大的情况,在大的情况下,加载整个流域效率不高,或者由于RAM限制,可能太大而无法在后处理器中打开。 在此示例中,提取了RisingBubble2D示例案例的顶部壁面,并可视化了作用在其上的压力场。 使用适当配置的sampledict:
functions
{
// Surfaces sample function object
surfaces
{
type surfaces;
surfaceFormat vtk;
writeControl writeTime;
interpolationScheme cellPoint;
fields (U p_rgh alpha.water);
surfaces
(
walls_constant
(
type patch;
patches ( top );
)
);
};
}
在risingBubble2D示例模拟案例的最后时间步上执行采样:
interFoam -postProcess -dict ./system/sample.patch -time 7
示例实用程序在模拟案例目录中生成postProcessing/surfaces/7子目录,内容如下:
?> ls postProcessing/surfaces/7/
walls_constant.vtp
创建一个patchVTK文件,在边界单元处写入三个物理场集。
4.2.5 多集合及曲面采样
sample实用程序允许对不同的sets和surfaces进行采样,因此sampledict存储这些元素的列表。 在RisingBubble2D/System Simulation case目录中准备了一个工作Sampledict配置文件。 它存储了本节中描述的所有示例的配置。 当需要来自sample的其他功能时,应用程序源代码提供的sampleDict字典应该是第一个查看的地方。
为了对仿真结果进行可视化,可以使用可视化应用程序ParaView。 Paraview是一个高级的开源应用程序,可以用于可视化现场数据,在paraview.org/wiki/paraview上有很多关于它的使用信息。 为了避免重复,本节只提供了在Paraview中可视化OpenFoam模拟结果所需的最小信息量。
paraView允许用户对数据执行一系列过滤器并可视化各自的输出。过滤器支持不同的操作,例如: 流线的计算,将矢量场可视化为字形,计算等轮廓表面,仅举几例。一些提出的OpenFOAM后处理工具也可以在paraView中复制,例如从点和沿线采样数据。
Paraview有一个用于OpenFoam数据的本地阅读器,可以直接用于显示OpenFoam案例数据。 无需编译ParaFoam,使用ParaView还提供了利用上游软件最新Verion的机会。 使用ParaFoam的绕行仍然有效,但不再需要。 为了使用本机Paraview Reader,case目录中需要有一个以.foam结尾的文件。 通常,此文件的命名方式与模拟案例目录相同,但选择并不重要。
下面选取Interfoam的RisingBubble2D实例,介绍Paraview的一些最基本的工作原理。 这个案例可以在第4/RisingBubble2D章下的示例库中找到。 首先,为了生成可视化的数据,必须执行模拟:
blockMesh
setFields
interFoam
touch risingBubble2D.foam
最后一行命令在本节的上下文中很重要。 它生成一个后缀为“foam”的空文件,这是Paraview打开OpenFoam Case数据所需的。 最后,ParaView用于打开案例文件,并作为后台进程启动,使当前终端可以访问进一步的命令。
paraview risingBubble2D.foam &
请注意,如果ParaView二进制文件不在计算机的路径上,那么您可能必须使用完整的目录路径调用它。 下面显示了一个示例,但需要进行调整以表示ParaView的安装位置。
/path/to/install/ParaView-5.7.0/bin/paraview risingBubble2D.foam
一旦Paraview启动,就会出现RisingBubble2d.foam文件,如图4.5所示。 否则,可以通过Open对话将ParaView文件浏览器指向RisingBubble2d.foam文件来打开OpenFoam案例。 在Paraview图形用户界面(GUI)的左侧,向用户显示用于选择网格部分和要读取的不同物理场的选项。 此窗口名为Properties,如果关闭了它,可以使用视图下拉菜单重新激活它。 Properties视图显示在图4.5中。
默认情况下,OpenFoam案例的内部网格和所有以网格为中心的物理场都被选择用于可视化。 当选择被接受时,通过单击属性窗口中的Apply按钮来读取物理场和网格。 可视化物理场的选择可以使用属性窗口上方的面板和管道浏览器,如图4.6所示。

最初,网格是用纯色着色的。 点击图4.6所示面板中的solid color卡,产生一个下拉菜单,其中包含所有可用的物理场。 初始时间步的alpha.water如图4.7所示。
在Paraview中,使用过滤器处理物理场是一个非常简单的过程。 在图4.6中,最常用的过滤器显示为主面板底部的按钮。 其他筛选器可在主面板上的筛选器下拉菜单中使用。 涉及不同过滤器使用的文档很多,包括Paraview社区Wiki页面(paraview.org/wiki/paraview)和官方文档。
一种常用的过滤器是Contour过滤器,可以用于可视化两种流体之间的界面。 Contour过滤器基于标量场计算指定值的等值面。 在本例中标量场是alpha.water。 这种操作实际上与4.2节中描述的等值面采样实用程序相当相似。 可以从主菜单Filters → Common → Contour中选择筛选器。 标量场alpha.water必须被选择为parameter,而0.5则被选择为等高线值。 当所有设置都按需要定义时,单击Apply将在右3D视图中显示结果。 最后,XY平面上的界面线应该是可见的,类似于图4.8。

Paraview中可视化的一个有趣方面是使用Selection Inspector枚举以单元格和/或点为中心的值和场数据的能力。 要开始,请确保在管道浏览器中选择了“rising-bubble-2d.foam”。 单击View-> Selection Inspector并在Selection Inspector窗口中,选中Invert Selection复选框。 在显示样式子窗口中,可以将选定内容的不透明度降低到0,以防止模糊单元格中显示的数值。 若要在每个单元格中显示alpha.water字段的值,请选择显示样式子窗口的单元格标签选项卡,并从标签模式下拉菜单中选择alpha.water。 在单元格标签中,可以指定所示值的格式,例如“%.1f”将是带有单个十进制数字的浮点格式。 图4.9显示了alpha.water字段的放大细节,显示的值以单元格为中心。
可以使用Paraview从顶部边界中提取值,而不是在4.2节中讨论的示例实用程序。 为了对patch进行采样,需要在Paraview中读取边界网格,而不仅仅是内部网格。 为此,在属性窗口的网格区域部分选择顶部补丁,如图4.10所示。
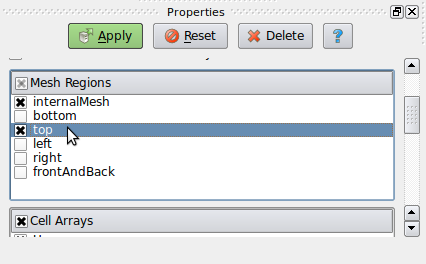
然后,通过使用Filter-> Alphabetical-> Extract Block Filter在Patches分支中选择顶部边界,将顶部补丁在管道中与大小写网格的其余部分隔离开来。 要直接绘制此补丁的数据而无需插值,请在管道浏览器中选择提取的块并选择Filters-> Data Analysis-> Plot Data。 在显示窗口(View-> Display)中,选择动态压力并跳到仿真的最后一个时间步。 结果图如图4.11所示。
在本节中,提供了使用ParaView可视化应用程序的工作流的绝对最小部分。 欲了解更多详情,请查阅互联网上的材料以及官方文件。
OpenFOAM 名称中的 FOAM 部分是 Field Operation and Manipulation 的首字母缩写。如前几章所述,FOAM 可能相当复杂,因为它们使用非结构化有限体积离散化技术,在几何形状复杂的求解域中以张量场的形式表示和操作物理特性。可以对离散张量场进行显式和隐式运算。场的变化受守恒定律的支配,被模拟为偏微分方程(PDE),PDE 的数值求解通常涉及组装和求解大型稀疏线性方程组。有时,PDE 是强耦合的,数值算法需要考虑这种耦合,例如动量方程和压力方程的耦合求解。由于矩阵尺寸通常较大,因此需要使用迭代求解算法来求解新场值的线性方程组[1, 3]。
只有当所选择的编程语言能够抽象出复杂的概念,并实现高效的计算和可移植性时,才有可能将上述 FVM 的所有方面转化为软件框架。在 OpenFOAM 中,这些概念包括:场、网格、离散方法、插值格式、状态方程、喷雾粒子系统、矩阵、矩阵存储格式、配置文件、并行编程等。即使是这份简短的清单,也能说明元素是如何占据不同的抽象层次的。例如,与字典数据结构相比,物理场和网格概念的抽象程度更高。通过抽象化,程序员可以有效地构建软件元素,对感兴趣领域中复杂概念的行为进行建模。这样,程序员就不必在脑海中浮现整个软件系统的图像,而是将注意力从一个相对孤立的概念转移到另一个概念上。建模良好的概念是那些内聚性强、相互耦合松散的概念。这样可以简化扩展,使软件更加模块化。例如,CFD 中的一个重要概念是有限体积网格,用于将流域离散化。
网格将保存各种几何和拓扑数据,如第1.3节和第2.1节所述。此外,需要使用不同(通常比较复杂)的功能来处理这些数据。以OpenFOAM和C++语言中的抽象为例,将有限体积网格的数据和相关功能封装到一个fvMesh类中。这使得程序员可以从网格的角度来思考,而不必考虑构建网格的数据结构和函数的所有细节。这种高度抽象的思维方式允许程序员编写将整个网格作为其参数之一的算法,这将使得算法接口更容易理解。否则,处理网格特定子元素的算法将有几十个参数,这在过程编程中经常出现。如果没有抽象,将会出现大量的全局变量,并且这些全局变量被各种算法访问,这将使得要想确定程序的流程变得非常困难。
注:本章的第一部分概述了OpenFOAM的软件设计,但是并不包括软件开发中的术语,这些应该独立学习。OpenFOAM是一个大型软件,学习软件开发是在OpenFOAM中开发新方法的必要条件。
C++编程语言支持更高抽象级别的编程,它是一种多范例语言,支持面向过程、面向对象、泛型及函数式编程范例。更高层次的抽象使得程序的实现更具可读性,但C++语言仍然具有非常高的计算效率,并且其是跨平台的。这些方面使得C++语言成为科学和计算软件开发的常见选择。
要了解OpenFOAM的不同部分是如何设计以及如何相互交互的,最好的方法是浏览源代码。
为了方便用户,OpenFOAM官方和扩展版本都支持通过Doxygen生成HTML文档,用户也可以在线获取为主开发版本生成的Doxygen文档。
生成的Doxygen文档允许使用者快速地查找相关类的信息。Doxygen文档系统生成可以使用Web浏览器浏览的HTML文档,其优点是可以查看带有链接元素的类图和协作图。这使得在研究类和算法之间的交互时特别有用。与使用文本编辑器浏览源代码相比,在HTML浏览器中跟踪指向基类的链接对大多数读者来说可能更有效。或者在使用OpenFOAM时,可以使用集成开发环境(IDE)浏览源代码。要开始学习OpenFOAM,我们推荐使用文本编辑器和Doxygen生成的文档。对于OpenFOAM新手来说,设置IDE以使用OpenFOAM本身可能是一项复杂的任务。
为了生成文档,需要在文件夹$WM_PROJECT_DIR/doc中执行命令Allwmake。
当Doxygen执行完毕后,可以利用浏览器打开文件$WM_PROJECT_DIR/doc/Doxygen/html/index.html。
此页面是OpenFOAM安装的本地生成HTML帮助的起始页面。或者也可以使用基于LaTeX的文档,该文档以PDF格式提供,但必须手动转换。
练习:利用Doxygen源代码文档查询并了解
tmp<Type>智能指针的类型是什么?
本节将介绍运行模拟的用户遇到的OpenFOAM的某些部分。
在第3章中设置初始条件和边界条件已经表明,用户具有相当大的灵活性可供他或她使用。无需编写任何附加代码,即可在输入(场或配置)文件中选择现有边界条件、插值和离散格式、粘度模型、状态方程和类似参数。
就底层实现而言,基于来自文件的输入数据选择边界条件相对复杂:在运行时基于用户定义的读取参数(边界条件类型)选择并实例化特定类的对象。通过运行模拟,用户可以直接或间接地接触OpenFOAM的以下部分:可执行应用程序(求解器、预处理实用程序、后处理实用程序)、配置系统(字典文件)、边界条件和数值运算(选择离散格式)。
5.2.1 Applications
可执行应用程序是由用户在命令行或通过GUI运行的程序。它们属于通常所说的客户端代码,它使用各种OpenFOAM库(即客户端)。
可执行应用程序(简称:应用程序)组织在如图5.1所示的目录结构中。通过在命令行中执行别名app或切换到applications目录,可以轻松访问Applications文件夹:
?> cd $FOAM_APP
OpenFOAM中的模块化设计和高级抽象使用户可以轻松地构建数学模型。利用OpenFOAM的高级DSL,也可以直接实现耦合偏微分方程组的不同求解算法。因此,随着时间的推移,可供选择的求解器应用程序非常广泛。求解器应用程序按组进行分类,如图5.2所示。

在test子目录中可以找到不同的测试应用程序。例如,directory测试应用程序测试dictionary类的主要功能,而parallel和parallel-nonBlocking应用程序实现用于在OpenFOAM中抽象并行通信的代码。在检查库源代码不足以理解类/算法如何工作的情况下,查看测试应用程序源代码可能非常有用。
5.2.2 配置系统
配置系统由配置(字典)文件组成:以类似于JSON的格式存储的文本文件。字典文件由用于构建称为dictionary的关联数据结构的分类输入数据组成。字典本质上是一个哈希表。
此数据结构在OpenFOAM中经常用来将键关联(映射)到值。
注:test应用程序是关于特定类和算法的非常有用的信息资源,其显示了如何使用类和算法。
在模拟案例目录中找到的各种字典文件包含不同的配置参数:边界条件、插值格式、梯度格式、数值求解器等。选择不同的元素以及正确初始化它们是在启动可执行应用程序后在运行时执行的。在运行时选择类型的过程称为运行时选择(Runtime Selection,RTS),它使用了相当多的软件设计模式和C++语言习惯用法。RTS过程相当复杂,其描述超出了本章的范围。在这一点上,重要的是要记住,它使OpenFOAM非常灵活,易于使用。
注:配置系统本身并不以抽象的形式存在,也不是作为单个类实现的。该系统由dictionary和IOdirectionary类的函数、输入/输出(IO)文件流以及运行时可选类中使用的RTS机制支持。
例如,OpenFOAM中的任何用户定义类都可以在运行时选择。此外,可以在模拟过程中修改类属性,只要修改了字典文件,就可以重新读取该文件,并将类属性设置为新值。
注:字典中定义的参数在修改后不会立即在可执行应用程序中更改。更改将在选中Modified后的下一个时间步开始时启用。
5.2.3 边界条件
边界条件应用于离散场,如第1.3节所述,并作为单独的类结构实现。因为它们是作为类实现的,所以RTS机制允许用户在运行时将边界条件类型和参数配置为字典条目。边界条件将在第10章中介绍,因此本章不会完全介绍它们。
5.2.4 数值操作
数值运算由求解器使用,负责模拟方程离散部分。用户通过修改模拟案例目录中的system/fvSchemes字典文件以选择不同类型的离散格式、插值格式或类似参数时。不同的数值运算有不同的性质,选择它们需要CFD方面的经验,理想情况下还需要数值计算方面的经验。
OpenFOAM中负责FVM数值操作的部分可以在控制台中执行别名foamfv,或者切换到适当的目录:
?> cd $FOAM_SRC/finiteVolume
数值计算由插值格式组成,然后离散微分算子使用插值格式对模型方程进行离散。CFD中常用的离散微分算子有:散度()、梯度()、拉普拉斯() 、旋度(),它们要么是显式的,要么是隐式的。显式运算符会生成新物理场作为结果;隐式运算符用于装置系数矩阵,其将数学模型的方程项离散化。另一方面,离散微分算子被实现为函数模板,由几何张量场参数实现参数化。微分运算符的这种通用实现使得在相同函数名下编写数学模型变得简单,这些函数名用于区分不同等级的张量场。由于运算符是作为函数实现的,因此组装不同的数学模型很简单:不同的函数调用序列会产生不同的模型。OpenFOAM具有命名相同的隐式和显式离散运算符,如显式散度和隐式散度。为了避免名称查找过程中的歧义,运算符被归类到两个C++名称空间下,并使用完全限定名称(FVC::为显式,FVM::为隐式)进行访问。
离散运算符是以张量参数为模板的通用算法,使用类特征系统来确定结果张量的秩。OpenFOAM中离散化的标准选择是基于散度定理,将算子计算委托给离散格式。那些对开发自己的离散格式感兴趣的人可能希望检查文件fvmDiv.c和CurectionScheme.c。这两个文件包含的实现都显示了散度项是如何处理方程离散的。下面列出的源代码包含将散度计算从操作符委托给对流方案的代码的实现。
return fv::convectionScheme<Type> ::New
(
vf.mesh(),
flux,
vf.mesh().divScheme(name)
)().fvmDiv(flux, vf);
可以通过RTS选择格式,但它们必须符合ConversationScheme.H中所描述的接口。这种灵活的设计可以用以下方式总结:
- 算子将离散化委托给格式
- 格式构成了运行时可选择的分层结构
- 要编写新的对流格式,只需继承自对流格式并添加RTS
- 实现对流格式后,不需要修改任何求解器应用程序代码
将运算符实现为函数模板并将其绑定到格式有很多优点,而且它为轻松扩展准备了框架,而无需对现有代码进行修改。详细描述离散化机制是如何实现的超出了本书的范围。
实现其他离散运算符的源代码可以在fvc和fvc子目录下的$foam_src/finiteVolume/finiteVolume中找到。目录fvc储显式离散运算符的实现,这会产生计算字段。目录fvm存储隐式离散运算符的实现,这导致代数方程系统的系数矩阵组装。
注:只要代码中有
fvc::运算符,其结果是一个物理场。当遇到fvm::运算符时,其结果是一个系数矩阵。
这些操作由求解器应用程序执行,与求解器代码的交互是在用户修改求解器以使其以不同方式运行时完成的。OpenFOAM支持通过fvOptions和function object修改运行时求解器(参见第12章),而不需要用户修改求解器代码。有关求解器应用程序以及如何编程实现新求解器的更多信息,请参见第9章。通常,当使用标准求解器获取模拟结果时,用户通常不会修改其代码。
OpenFOAM中的高级抽象允许用户非常快速地编写新的求解器和求解算法。OpenFOAM的高抽象层几乎可以用作CFD编程语言(DSL)-也称为方程模拟([2])。例如,以标量属性T的标量传输的数学模型为例: 方程(5.1)描述了由具有速度U的被动对流、具有扩散系数k的扩散以及源项S组成的场T的输运,离散化运算符是模板函数,可以对不同张量场进行运算,因此在标量场上它们在OpenFOAM中产生以下模型方程:
ddt(phi) + fvm::div(phi,T) + fvm::laplacian(k,T) = fvc::Sp(T)
描述模型的代码由离散运算符ddt、div、Laplacian和Sp组成。
插值算法也属于OpenFOAM中的数值运算。最常用的插值格式建立在非结构化网格的owner-neighbour寻址的基础上,插值得到网格面中心的值。在此基础上,构建了插值格式的树状类层次结构,如图5.3所示,其根节点为SurfaceInterpolationScheme。
从软件设计的角度来看,内插格式被封装到形成类层次结构的类中。一些格式共享属性和功能,因此将它们组织为类层次结构是有意义的。作为这种组织的结果,RTS机制允许用户在仿真开始时(或甚至在仿真期间)选择不同的离散化/内插格式,而不需要重新编译程序代码。
5.2.5 后处理
可以在仿真之后或仿真期间执行后处理。在模拟完成后进行后处理时,将使用PostProcess应用程序。OpenFOAM提供了另一种独特的方法,通过调用函数对象在模拟过程中对数据进行后处理。
后处理应用程序与OpenFOAM一起分发,或者由用户自己编写。
在编写后处理应用程序之前,建议检查是否已经存在具有所需功能的应用程序。OpenFOAM提供了大量实用程序可供选择。
目录$FOAM_APP/UTILITIES/PostProcessing中包含与OpenFOAM一起分发的所有后处理应用程序,这些应用程序被归入不同的组。
目录$FOAM_APP/UTILITIES/PostProcessing及其子目录是查找现有后处理应用程序的第一个位置,如图5.4所示。如果需要编写新的应用程序,则现有应用程序的某些部分很可能可以用作开发的起点。后处理应用程序通常用于基于模拟期间存储的场来计算一些整数值,或者对流量域的特定部分中的场值进行采样。然而,这绝不能仅限于此。基本上,您可以使用后处理应用程序在后处理步骤中计算任何内容。

与后处理应用程序不同,function objects是在模拟运行期间调用的。术语function object来自C++语言术语,其中它表示可调用的类,因为它实现了调用运算符:Operator()()。函数对象基本上是封装到类中的函数,这是有利的,例如当函数在执行后需要存储有关其状态的信息时。例如,在模拟中计算平均最大压力的函数对象可以在压力值超过规定值时停止模拟。这样的函数需要访问最大压力值,并且需要存储计算运行平均值所需的数据。因此,这两个属性被封装到函数对象类中。有关OpenFOAM中函数对象的更多信息,请参见第12章。
在上一节中,由于讨论了用户在运行模拟时接触到的OpenFOAM的部分内容,所以只简要介绍了一些类。以下各节提供了OpenFOAM中一些选定和常用类的更深入的见解和最佳实践。
5.3.1 Dictionary
dictionary类是OpenFOAM用户最早与之交互的类之一。虽然dictionary类接口不是很复杂,但对于新手用户来说,它的某些方面可能并不明显。
从字典中读取数据
读取字典条目值是使用dictionary类的最基本形式。dictionary类接口提供了多个可用于读取数据的方法。getOrDefault方法就是最常用的例子,因为它不仅提供对指定字典条目的读访问,而且如果没有找到条目,其还能够指定一个默认值。这消除了因缺少非关键输入值而导致的运行时错误。
创建的调用形式如:
const auto & solution(mesh.time().solutionDict());
const auto name(solution.getOrDefault<word> ("parameters1"));
const auto vector1(solution.getOrDefault<vector> ("vector1"));
如上面的代码所示,getOrDefault需要的不仅仅是参数的名称才能读取。它还需要一个带有要在字典中查找的数据类型名称的模板参数。
访问目录
目录包含字典的子字典的名称。在下面的示例中,可以访问由Foam::Time类读取的fvSolution文件的目录:
const dictionary &fvSolutionDict(mesh.time().solutionDict());
Info << fvSolutionDict.toc() << endl;
访问子字典
在开发OpenFOAM时,经常会遇到访问子字典的问题,因为在OpenFOAM中开发的自定义类或求解算法由字典文件配置。假设constant目录中的字典文件A包含以下数据:
axis (1 0 0);
origin (5 10 15);
type "modelA";
modelA
{
name "uniform";
}
为了访问A文件中的子字典modelA,可以使用下面的代码:
const dictionary dict(fileName("constant/A"));
const auto& subDict(dict.subDict("modelA"));
5.3.2 量纲类型
Dimensioned类型将单位附加到标量、矢量和张量上。其扩展了张量运算以包括度量单位:OpenFOAM中的量纲。如速度与动量都是矢量,但它们不能进行代数相加,因为他们的量纲不同。OpenFOAM中的量纲检查是通过类模板dimensioned<Type> 来实现的。
dimensioned<Type> 是一个包装器(适配器)类,其将张量算法的计算委托给经过包装的tensor类,并将量纲检查工作委托给经过包装的dimensionSet对象。通过研究dimensioned<Type> 类模板的算术运算符,可以实现如下所示的+=运算符:
template<class Type>
void Foam::dimensioned<Type> :: operator+=
(
const dimensioned<Type> &dt
)
{
dimensions+ += dt.dimensions_;
value_ += dt.value_;
}
可以看出,有两个算术运算正在执行:一个是对量纲(单位)的运算,另一个是对张量的数值的运算。dimensionSet类的算术运算符负责量纲的检查过程。dimensionSet类的+=算术运算符的源代码如下所示:
bool Foam::dimensionSet :: operator+= (const dimensionSet &ds) const
{
if(dimensionSet::debug && *this != ds)
{
FatalErrorIn("dimensionSet::operator+=(
const dimensionSet&) const")
<< "Different dimensions for +=" << endl
<< " dimensions : " << *this << " = "
<< ds << endl << abort(FatalError);
}
}
这提供了足够的信息来准确总结量纲检查是如何执行的:如果量纲检查已打开,则当对不同(!=)量纲的集合执行加法操作时,将生成一个致命错误,该错误将中止程序执行。dimensionSet类将量纲实现为一组物理度量的整数指数,如下所示:
//- Define an enumeration for the names of the dimension exponents
enum dimensionType
{
MASS, // kilogram kg
LENGTH, // metre m
TIME, // second s
TEMPERATURE, // Kelvin K
MOLES, // mole mol
CURRENT, // Ampere A
LUMINOUS_INTENSITY // Candela Cd
};
如下面的代码所示,量纲检查运算符是根据相等运算符==来执行的。检查过程会迭代操作dimensionSet的量纲。通过循环测试,如果量纲指数之间的差异的大小足够大(> smallExponent),可以认为集合不相等。
bool Foam::dimensionSet::operator==(const dimensionSet& ds) const
{
for (int Dimension=0; Dimension < nDimensions; ++Dimension)
{
if(mag(exponents_[Dimension] - ds.exponents_[Dimension])> smallExponent)
{
return false;
}
}
return true;
}
SmallExponent的值是类静态变量:
static const scalar smallExponent;
其被初始化为SMALL,对于双精度scalar,其值为。
通过将$WM_PROJECT_DIR/etc/control Dict中dimsionedSet类的debug标志设置为ON,可以打开量纲检查:
DebugSwitches
{
Analytical 0;
APIdiffCoefFunc 0;
...
dictionary 0;
dimensionSet 1;
mappedBase 0;
...
对于+=运算符,给出的结论与其他量纲张量算术运算完全相同。默认情况下,量纲检查处于激活状态,通常不应在OpenFOAM中将其取消激活。即使自定义应用程序以无量纲的形式实现公式,这些方程式也会使用应该是无量纲的数字进行缩放。量纲检查系统可以检查例如雷诺数:
auto Re = Foam::mag(U) * L/mu;
Info << Re.dimensions() << endl;
雷诺数实际上是无量纲的,在这种情况下,输出的是仅包含零的dimensionSet。然而,如果在计算(例如L)时出错,依赖SI测量单位系统的尺寸检查将发现这一点。因此,即使方程是以无量纲形式编写的,也应该使用量纲检查来检查缩放错误。
OpenFOAM中的许多具有复杂名称的类模板,都提供了typedef。在c中,
typedef关键字允许程序员定义较短和更简洁的类型名称。尽管这个typedef可能不会比原来短很多,但它至少保存了部分的输入。在dimensioned的情况下,重点不是名称长度,而是代码样式——dimensionedVector是camel case中的一个名称,用于OpenFOAM应用程序级代码中的类型。
dimensioned<type> 最常用的同义词是dimensionedScalar和dimensionedVector,在以下示例中使用。此外,请注意,dimensioned类型的构造方式比目前描述的方式稍微复杂一些。标注类型不需要张量值和dimension集合,而是需要一个附加参数:name。例如,如果二维矢量对象按以下方式构造:
dimensionedVector velocity
(
"velocity",
dimLength/dimTime,
vector(1,0,0)
);
dimensionVector momentum
(
"momentum",
dimMass * (dimLength / dimTime),
vector(1,0,0)
);
请注意,有一些预定义的dimensionSet对象用于初始化速度和动量向量对象:dimLength、dimTime和dimMass。它们是常量和全局对象,可以在源文件DimensionSets.C中找到:
const dimensionSet dimless(0,0,0,0,0,0,0);
const dimensionSet dimMass(1, 0, 0, 0, 0, 0, 0);
const dimensionSet dimLength(0, 1, 0, 0, 0, 0, 0);
const dimensionSet dimTime(0, 0, 1, 0, 0, 0, 0);
const dimensionSet dimTemperature(0, 0, 0, 1, 0, 0, 0);
const dimensionSet dimMoles(0, 0, 0, 0, 1, 0, 0);
const dimensionSet dimCurrent(0, 0, 0, 0, 0, 1, 0);
const dimensionSet dimLuminousIntensity(0, 0, 0, 0, 0, 0, 1);
可以使用基本的物理量纲来构造复杂的量纲(例如N=kgm/s2),所以在定义自己的dimensionSet时,使用全局预定义的尺寸集对象来提高代码的可读性。
继续讨论量纲类型的算术,并将速度添加到动量中,如下所示:
momentum += velocity;
将会导致下面的错误提示:
--> FOAM FATAL ERROR:
Different dimensions for +=
dimensions : [1 1 -1 0 0 0 0] = [0 1 -1 0 0 0 0]
From function dimensionSet::operator+=(const dimensionSet&) const
in file dimensionSet/dimensionSet.C at line 179.
FOAM aborting
OpenFOAM中的量纲检查过程在运行时执行。因此,在量纲操作中包含错误的代码仍然会被编译,但不会运行。OpenFOAM中的量纲检查错误可以通过调试器(例如gdb)轻松调试,前提是OpenFOAM和自定义代码是在调试模式下编译的。
练习:使用前面提到的调试标志关闭量纲检查,并运行动量和速度的算术加法
5.3.3 智能指针
指针是一种特殊的变量,其存储对象的内存地址,可以用来引用该对象。在c中,可以通过值或引用来传递对象,后者对于较大对象来说明显更快。这不仅更快,而且在内存使用方面更加保守,因为没有数据被临时复制。与只使用指针相比,按值返回较大的对象并将其作为函数参数传递在计算上要昂贵得多。
如下面的代码:
result = function(input);
可以改成以非常量引用传递给函数的result参数:
function(result,input);
离散化算法(运算符)首选第一种选择,因为它们通常由算术表达式组成,用于建立数学模型。例如,考虑取自interFoam求解器的动量守恒方程代码:
fvVectorMatrix UEqn
(
fvm::ddt(rho,U)
+ fvm::div(rhoPhi,U)
+ turbulence-> divDevRhoReff(rho,U)
);
作用于场rho、U及rhoPhi的算子之和将是一个系数矩阵(fvVectorMatrix)。因此,上述代码必须满足以下几点:
- fvVectorMatrix必须是可拷贝构造的
- 所有操作符必须返回一个fvVectorMatrix
- fvVectorMatrix的加法运算符必须返回一个fvVectorMatrix
如果运算符ddt和div被实现为具有可修改参数的函数,则不可能轻松地编写数学模型(通常称为方程模拟)。函数返回的矩阵非常大,因此按值返回它们会带来创建临时对象的代价。借助于OpenFOAM智能指针,OpenFOAM避免以不依赖编译器优化的显式方式创建不必要的复制操作。智能指针在插值函数中初始化,并通过值返回。涉及方程离散化的其他操作,如对流格式,也是如此。例如,高斯对流格式的fvmDiv散度算子初始化了这样一个智能指针(tmp<fvMatrix<Type> > ),如下所示 :
tmp<fvMatrix<Type> > tfvm
(
new fvMatrix<Type>
(
vf,
faceFlux.dimensions()* vf.dimensions()
)
);
然后它执行计算,负责定义所示系数矩阵中的元素.
fvm.lower() = -weights.internalField()*faceFlux.internalField();
fvm.upper() = fvm.lower() + faceFlux.internalField();
fvm.negSumDiag();
forAll(vf.boundaryField(), patchI)
{
const fvPatchField<Type> & psf = vf.boundaryField()[patchI];
const fvsPatchScalarField& patchFlux = faceFlux.boundaryField()[patchI];
const fvsPatchScalarField& pw = weights.boundaryField()[patchI];
fvm.internalCoeffs()[patchI] = patchFlux*psf.valueInternalCoeffs(pw);
fvm.boundaryCoeffs()[patchI] = -patchFlux*psf.valueBoundaryCoeffs(pw);
}
if (tinterpScheme_().corrected())
{
fvm += fvc::surfaceIntegrate
(
faceFlux*tinterpScheme_().correction(vf)
);
}
然后,在函数开始时初始化的智能指针被按值返回。
return tfvm;
按值返回有限体积矩阵(tfvm)的智能指针的结果是对智能指针进行复制操作。然而,智能指针的拷贝和整个矩阵对象的拷贝之间有一个显著的区别:指针的值只是矩阵的地址,而不是整个矩阵本身。这种方法大大增加了执行的效率。
避免不必要的复制操作有一个常用的简短名称:复制消除。在c编程语言中,可以通过不同的方式来执行拷贝消除:编译器优化(返回值优化,命名为RVO),表达式模板(ET),或者使用c 11语言标准提供的右值引用和移动语义。
通常,当使用指针时,它们指向使用运算符new在堆上创建的对象:
someType *ptr = new someType(argments...);
由于c编程语言不支持自动垃圾收集,因此只能由程序员负责释放资源。
因此,每次调用new操作符之后都需要相应地调用delete操作符。当然,对delete操作符的调用必须放在适当的位置,例如类析构函数。这就可能导致程序员忘记删除指针,从而导致内存泄漏。作为错误的另一个来源,访问已删除指针引用的内存部分将导致未定义的行为。这两个问题都会发生在运行时,通常是难以发现和调试的错误源。为了避免这两个问题,需要避免直接处理原始指针。在c中,原始指针的处理已被称为资源获取初始化(RAII)的习惯用法所取代。
RAII习惯用法指出,原始指针需要封装到一个类中,该类的析构函数负责删除指针并在代码中的适当位置释放资源。在这样的类中调整原始指针,并为调整后的原始指针提供不同的功能,导致了所谓的智能指针的发展。不同的智能指针存在并提供不同的功能。OpenFOAM实现了两个这样的智能指针:autoPtr和tmp。
只要环境变量是通过源码库的etc/ bashrc配置脚本来设置的,例子的应用程序代码就可以在$PRIMER_EXAMPLES_SRC/applications/test/文件夹下获得。那些有兴趣按照接下来的章节介绍的教程一步步学习的读者,需要创建一个新的可执行的应用程序:testSmartPointers。在OpenFOAM中创建新的应用程序是很简单的,因为有脚本可以为应用程序生成文件框架。要创建一个新的应用程序,需要选择一个目录来放置应用程序的代码,并执行以下命令:
mkdir testSmartPointers
cd testSmartPointers
foamNew source App testSmartPointers
sed -i 's/FOAM/APPBIN/ FOAM_USER_APPBIN/g' Make/options
最后一行将应用程序二进制文件的放置目录从平台目录替换为用户应用程序二进制文件目录。
将你自己的应用程序构建到FOAM_USER_APPBIN中是一个很好的做法,这需要在Make/options构建配置文件中指定。在本节中,使用的是gcc编译器。在阅读文本中关于特定编译器标志的内容时,要注意到这一点
5.3.3.1 使用autoPtr智能指针
为了说明如何使用autoPtr,需要为使用的示例定义一个新类。该类应该在每次调用其构造函数和析构函数时通知用户。在本例中,它继承自基本字段类模板字段,并命名为infoField。可以使用任何其他类,因为编译器对复制操作执行的优化不依赖于对象的大小。
首先,可以如下所示定义infoField类模板:
template<typename Type>
class infoField : class Field<Type>
{
public:
infoField():Field<type> ()
{
Info << "empty constructor" <<endl;
}
infoField(const infoField& other):Field<Type> (other)
{
Info << "copy constructor" << endl;
}
infoField(int size, Type value) : Field<Type> (size,value)
{
Info << "size,value constructor" << endl;
}
~infoField()
{
Info << "destructor" << endl;
}
void operator=(const infoField & other)
{
if(this != &other)
{
Field<type> :: operator=(other);
Info << "assignment operator" << endl;
}
}
};
该类模板继承自Field
- 空构造函数
- 拷贝构造函数
- 析构函数
- 赋值运算符
每次使用这些函数时,一个Info语句会向标准输出流发出特定调用的信号。这样做的目的只是为了获得哪个函数被执行的信息。
为了继续这个例子,需要定义一个函数模板,其按值返回一个对象。
template<typename Type>
Type valueReturn(Type const & t)
{
// One copy construction for the temporary.
Type temp = t;
// ... operations (e.g. interpolation) on the temporary variable.
return temp;
}
为了减少不必要的输入,例子中使用的类型名称被缩短了。
// 简写类型名
typedef infoField<scalar> infoScalarField;
在主函数中,实现了以下几行:
Info << "Vlaue construction:";
infoScalarField valueConstructed(1e7, 5);
Info << "Empty construction:";
infoScalarField assignedTo;
Info << "Function call" << endl;
assignedTo = valueReturn(valueConstructed);
Info << "Function exit" << endl;
用Debug或Opt选项编译和执行应用程序,将产生完全相同的结果,尽管Debug选项可以打开编译器的优化。正如本节开头所提到的:编译器非常善于识别这样一个事实,即返回的临时对象在赋值后就被丢弃了。不使用几何场的另一个好处是,这个小的示例程序不需要在OpenFOAM仿真案例目录下执行。它可以直接从存储代码的目录中调用。执行该程序将产生以下输出:
?> testSmartPointers
Value construction : size, value constructor
Empty construction : empty constructor
Function call
copy constructor
assignment operator
destructor
Function exit
destructor
destructor
单独考虑输出的每一行,同时将其与valueReturn函数代码进行比较,有趣的是发现临时返回变量从未被构造。在函数的返回语句中缺少一个拷贝构造,因为该函数是通过值返回的,同时也缺少一个相应的析构器调用。这种行为的原因是编译器自动进行的拷贝消除优化,即使在调试模式下也是如此。为了消除这种优化,可以在Make/options中添加一个额外的编译器标志:
EXE_INC = \
-I(LIB_SRC)/finiteVolume/lnInclude \
-fno-elide-constructors
EXE_LIBS = \
-lfiniteVolume
gcc编译器标志-fno-elide-constructors将阻止编译器进行优化,这对跟踪valueReturn中发生的事情很重要,否则会被编译器优化掉。
注意:记得在执行wmake之前调用wclean。对Make/options文件的修改不会被wmake构建系统识别为需要重新编译的源代码修改。
用上面定义的选项文件编译和运行应用程序,结果是以下输出:
?> testSmartPointers
Value construction : size, value constructor
Empty construction : empty constructor
Function call
copy constructor # Copy construct tmp
copy constructor # Copy construct the temporary object
destructor # Destruct the tmp - exiting function scope
assignment operator # Assign the temporary object to assignedTo
destructor # Destruct the temporary object
Function exit
destructor
destructor
输出显示了临时对象的不必要的创建和删除。通过在函数返回的地方执行对象的就地构建来避免临时对象的拷贝,已经成为编译器的一个标准选项。经常发生的情况是,即使在Debug模式下用编译器标记-O0 -DFULLDEBUG抑制优化,也不能禁用这个功能。
为了禁用构造函数复制的优化,必须在Make/options中明确传递编译器标志-fno-elide-constructors。
上面的例子有一个主要目的:表明在表达式中没有必要使用autoPtr智能指针,因为在表达式中无论如何都会返回一个命名的临时对象。在现代编译器上,即使在调试模式下编译(对于OpenFOAM来说,这意味着将$WM_COMPILE_OPTION设置为调试),这种优化也是默认开启的。
一些最突出的使用autoPtr的例子是在采用RTS的模型中,例如湍流模型和fvOptions。特定的基类是基于用户在字典中指定的关键字而实例化的。以turbulenceModel类为例,基类被用作autoPtr的模板参数,例如在求解器应用程序中,RTS可以将特定的湍流模型实例化到autoPtr中。RTS允许类用户在运行时将类层次中的特定类的对象进行实例化。以这种方式实例化对象使c能够通过基类指针或引用访问派生类对象。这通常被称为动态多态性。
本书不可能涵盖OpenFOAM使用的c语言标准的所有细节。只要遇到听起来不熟悉的c结构,就应该到其他地方去查找。
湍流模型通常在特定求解器的createFields.H中实例化,它被包含在时间循环开始之前。相关的代码行如下所示:
autoPtr <incompressible::RASModel> turbulence
(
incompressible::RASModel::New(U,phi,laminarTransport)
);
很明显,一个autoPtr被用来存储湍流模型。如果使用原始指针来访问RASModel对象,那么在求解器的代码中还需要另一行来删除原始指针,以便在求解器结束时去分配内存。由于autoPtr是一个智能指针,这种删除是在autoPtr析构器中自动执行的。原始指针方法的代码(幸运的是在OpenFOAM中没有任何地方使用)看起来是这样的。
incompressible::RASModel* turbulence = incompressible::RASModel::New(U, phi, laminarTransport)
在求解器代码的末尾,需要有以下几行:
delete turbulence;
turbulence = NULL;
当然,对于一个单一的指针来说,添加行来释放资源可能不是问题。然而,RTS用于:传输模型、边界条件、fvOptions、离散格式、插值格式、梯度格式等等。所有这些对象与场和网格这样的东西相比都很小,所以它们可以通过值来返回吗?从效率的角度来看--是的,特别是考虑到所有现代编译器都实现了返回值优化(RVO)。从灵活性的角度来看--没有机会这样做,因为动态多态性依赖于通过指针或引用的访问。保持运行时的高灵活性,意味着要依赖指针或引用。
当RTS被用来在运行时选择对象时,使用autoPtr或tmp是必要的。
下面的例子研究了 autoPtr 接口和它基于所有权的复制语义。autoPtr拥有它所指向的对象。这是预期的,因为RAII要求智能指针处理资源释放,所以程序员不必这样做。因此,创建autoPtr的副本是很复杂的--复制一个autoPtr会使原来的autoPtr失效,并将对象的所有权转移到副本中。要看这是如何工作的,请考虑下面代码段的主函数。
int main()
{
// Construct the infoField pointer
autoPtr<infoScalarField> ifPtr (new infoScalarField(1e06, 0));
// Output the pointer data by accessing the reference -
// using the operator T const & autoPtr<T> ::operator()
Info << ifPtr() << endl;
// Create a copy of the ifPtr and transfer the object ownership
// to ifPtrCopy.
autoPtr<infoScalarField> ifPtrCopy (ifPtr);
Info << ifPtrCopy() << endl;
// Segmentation fault - accessing a deleted pointer.
Info << ifPtr() << endl;
return 0;
}
需要注意的是,一旦对autoPtr对象进行了拷贝,所指向的对象的所有权就会被转移。注释掉导致段故障的那一行,结果应用程序的输出看起来像这样。
?> testSmartPointers
size, value constructor
1000000{0}
1000000{0}
destructor
很明显,尽管autoPtr对象是通过值传递,也只会引用infoScalarField类的一个构造函数和析构函数。因此,autoPtr可以被用来节省不必要的复制操作。
5.3.3.2 使用tmp智能指针
tmp智能指针通过执行引用计数来防止对象的不必要的复制。引用计数是指同一对象被传递的过程。在这种情况下,引用计数是通过refCount类进行的。这个数据结构是任何应该存储在tmp智能指针中的类的重要基类。它被智能指针包裹着,每次对智能指针进行复制或赋值时,这个对象的引用数量都会增加。
遵照RAII,临时工指针的析构器负责销毁被包装的对象。该析构器检查该对象在当前作用域中的refCount数量。如果这个数字大于0,析构器就简单地将refCount减少1,并允许该对象继续生存。一旦在被包装对象的 refCount 达到 0 的情况下调用析构器,析构器就会删除该对象。
注意:tmp智能指针的定义可以在$FOAM_SRC/OpenFOAM/memory/tmp中找到。
使用tmp智能指针时有一个问题:指针类模板不负责计算引用。引用计数是由封装的类型来实现的。在检查类的析构器时,可以很容易地检查这一点。
template<class T>
inline Foam::tmp<T> ::~tmp()
{
if (isTmp_ && ptr_)
{
if (ptr_-> okToDelete())
{
delete ptr_;
ptr_ = 0;
}
else
{
ptr_-> operator--();
}
}
}
ptr_属性是一个类型为T的对象的包装好的原始指针,解构器试图访问两个成员函数。
- T::okToDelete()
- T::operator--()
因此,被包装的对象必须遵守一个特定的类接口。测试这个问题的另一个方法是尝试用一个琐碎的类来使用tmp,这个类可以定义如下。
class testClass {};
然后试图将这个类包装成一个tmp智能指针。
tmp<testClass> t1(new testClass());
上述代码导致以下错误。
tmpI.H:108:9: error: ‘class testClass’
has no member named ‘okToDelete’ if (ptr_-> okToDelete())
tmpI.H:115:13: error: ‘class testClass’
has no member named ‘operator--’ ptr_-> operator--();
通过这个错误,编译器抱怨上述成员函数没有被testClass实现的事实。
由于OpenFOAM使对象执行引用计数,所以它被封装在一个此类对象继承的类中,名为refCount。refCount类实现了引用计数器和相关的成员函数。
为了在OpenFOAM中使用tmp
,被包装对象的类型T应该继承于refCount。
如果testClass被修改为继承于refCount。
class testClass : public refCount {};
然后可以用tmp来包装。为了了解引用计数是如何工作的,以及如何避免不必要的对象构造,tmp可以与infoScalarField类一起使用,该类在描述autoScalarField的例子中使用过,然后可以用tmp包装。为了了解引用计数是如何工作的,以及如何避免不必要的对象构造,tmp可以与infoScalarField类一起使用,该类在描述autoPtr的例子中使用。refCount类允许用户通过成员函数refCount::count()获得当前引用计数的信息,这在下面的例子中使用。人工作用域被用来减少临时工对象的寿命,以便它们的析构器被调用。在普通程序代码中,当出现嵌套函数调用或循环时,会出现这种情况。下面是例子的代码。
tmp<infoScalarField> t1(new infoScalarField(1e06, 0));
Info << "reference count = " << t1-> count() << endl;
{
tmp<infoScalarField> t2 (t1);
Info << "reference count = " << t1-> count() << endl;
{
tmp<infoScalarField> t3(t2);
Info << "reference count = " << t1-> count() << endl;
} // t3 destructor called
Info << "reference count = " << t1-> count() << endl;
} // t2 destructor called
Info << "reference count = " << t1-> count() << endl;
这将导致以下命令行输出。
> ? testSmartPointers
size, value constructor
reference count = 0
reference count = 1
reference count = 2
reference count = 1
reference count = 0
destructor
来自infoField类的单个构造器和相应的析构器输出显示,尽管tmp对象被作为函数参数按值传递,但只进行了一次构造和破坏。
5.3.4 体积场
第10章深入讨论了边界场和边界条件,包括它们背后的理论。
volume field是那些通常用于存储单元中心的场变量值。根据该场变量存储的张量类型,可以使用volScalarField、volVectorField或volTensorField。也有表面场和点场,它们分别在面中心和单元角点存储物理场值。请注意,所有提到的场的构造都是相似的,与它们的类型无关。
在OpenFOAM中,将数值映射到非结构化网格单元的场由通用的GeometricField类模板实现的。具体的场,如体积场、表面场和类似的其他物理场,则通过实例化GeometricField类模板和特定的模板参数,以具体类的形式生成。正如在关于量纲类型的章节中所指出的,OpenFOAM中用于场的类型名称为了方便使用typedef关键字而被缩短。
涉及volScalarField等场变量的编译错误会导致c模板错误,这些错误相当长,读起来不直观。因为这些字段是GeometricField模板的实例,可以调查GeometricField类的模板源代码,以获得更多关于错误的信息。
在能够使用一个物理场的对象之前,它必须被构造,就像任何其他对象一样。类接口有几个重载构造函数,根据特定的情况可能会派上用场。简单的构造函数是复制构造函数。
const volScalarField pOld(p);
顾名思义,它构造了一个原始数据的副本,其类型是相同的。然而,为了使用这个构造函数,首先必须有一个volScalarField。有两种方法可用于此:要么从文件中读取场变量的数据,要么从头开始生成它。基于输入文件的场的初始化是相当直接的,在OpenFOAM的每个求解器或处理程序的createFields.H文件中可以找到这样的例子。为此,IOobject被用来执行访问该文件的文件系统级输入输出,并作为一个封装类来使用。它是物理场所需要的,以便从文件中构建。
volScalarField T
(
IOobject
(
"T",
runTime.timeName(),
mesh,
IOobject::MUST_READ,
IOobject::AUTO_WRITE
),
mesh
);
上面的代码根据T文件的内容初始化volScalarField,T文件必须存在于时间目录中(或者至少是0-目录)。当然,T文件必须有适当的格式,以便在IOobject的构造函数中使用,然后被用来构造volScalarField。如果T文件不存在,由于IOobject::MUST_READ指令,代码的执行将停止。其他指令也可以选择,这取决于特定的需要。剩下的两个选项是READ_IF_PRESENT和NO_READ。第一个选项只在文件存在于任何一个时间目录中时才读取,否则就通过提供的默认值构建。NO_READ从不从文件中读取任何东西,只是构建物理场。
在某些情况下,需要在不从文件中读取数据的情况下构建物理场。通量场就是一个很好的例子。
surfaceScalarField phi
(
IOobject
(
"phi",
runTime.timeName(),
mesh,
IOobject::READ_IF_PRESENT,
IOobject::AUTO_WRITE
),
linearInterpolate(rho*U) & mesh.Sf()
);
如果文件存在,则phi由字段数据本身构建。否则直接从速度场计算通量。
这显示了T和phi的构造的不同;两者都以IOobject作为第一个参数,但T的构造以polyMesh作为第二个参数,而phi则以surfaceScalarField作为第二个参数。如果你仔细看看$FOAM_SRC/OpenFOAM/fields/GeometricFields/GeometricField/GeometricField.H,你会发现GeometricField类有大量的重载构造函数,它是OpenFOAM中所有场的基类。你可以根据特定的需要使用所有的构造函数。
5.3.4.1 访问网格数据
特定的单元可以通过调用特定场的访问操作符Type&operator[](const label cellI)并将所需的网格标签作为参数来处理。当对任何物理场进行算术运算时,不建议在网格之间进行运算。相反,应该使用物理场算术运算符。
在应用级程序代码中使用场变量的循环会降低代码的可读性,并可能导致计算效率的显著下降。
总之,这种选择特定网格的方法只能在需要使用网格子集进行计算时使用。下面的代码显示了一个如何选择压力场和速度场的网格的例子。
labelList cellIDs(3);
cellIDs[0] = 1;
cellIDs[1] = 42;
cellIDs[3] = 39220;
forAll(cellIDs, cI)
{
Info << U[cellIDs[cI]] << tab << p[cellIDs[cI]] << endl;
}
5.3.4.2 访问边界数据
正如第1章所述,内部场值与边界场值是分开的。这种网格中心和边界(面中心)值的逻辑分离是由支持FVM的数值插值方式所定义的。
将边界场值与内部场值分开,对OpenFOAM中算法的并行化方式有重要影响。数值操作在OpenFOAM中使用数据并行化,域被分解成子域,数值操作在每个独立的子域上执行。因此,许多并行进程被执行,需要跨越分解(处理器)的边界相互通信。将进程边界建模为边界条件的结果是,在OpenFOAM中基于owner-neighbor寻址的所有数值操作的自动并行化。非结构化的FVM离散化的自动并行化是OpenFOAM的一个值得注意的特点。
下面的例子显示了如何访问边界补丁出口的体积标量场压力的边界场值。关于边界场及其与内部场的区别的更多信息,请参考第10章。出口处的边界场可以根据映射到边界网格patch(边界网格的一个子集)名称的边界ID来找到。
const label outletID(mesh.boundaryMesh().findPatchID("outlet"));
然后使用GeometricField:: boundaryField成员函数访问边界场。
const scalarField& coutletPressure = pressure.boundaryField()[outletID];
体积场pressure有一个成员函数boundaryField,它返回一个指向边界场的指针列表。出口边界字段在该指针列表中的位置由出口ID标签(索引)定义。上面的代码片段将边界物理场设置为常数引用outletPressure,然而对边界物理场的非常数访问是由成员函数提供的。这可以通过观察GeometricField类模板的声明来确认。
GeometricBoundaryField &boundaryFieldRef();
GeometricBoundaryField是一个类模板,它的参数与GeometricField相同,这个类模板的定义被放置在GeometricField类接口的public部分。
- J. H. Ferziger and M. Perić. Computational Methods for Fluid Dynamics. 3 rd rev. Ed. Berlin: Springer, 2002.
- Hrvoje Jasak, Aleksandar Jemcov, and Željko Tuković. “OpenFOAM: A C++ Library for Complex Physics Simulations”. In: Proceedings of the International Workshop on Coupled Problems In Numerical Dynamics (CMND 2007) (2007).
- H. K. Versteeg and W. Malalasekra. An Introduction to Computational Fluid Dynamics: The Finite Volume Method Approach. Prentice Hall, 1996.
任何规模较大的软件项目都需要一定程度的组织。从目录组织到版本控制系统(Version Control System,VCS),代码开发的许多方面都需要标准实践。
由于数值模拟涉及大量的数据集和计算操作,CFD应用程序的开发非常重视计算效率。即使不仔细考虑简单的算法,也会造成严重的瓶颈。使用适当的工具,通常可以更快、更容易地解决代码中的问题,如执行错误(Bug)或计算瓶颈。
在高性能计算(HPC)集群上以并行模式运行仿真需要用户首先在集群上安装OpenFOAM。即使集群上已经安装有完整的OpenFOAM,拥有该主题的背景知识也可以让用户更准确地评估可能的安装问题并将其报告给集群管理员。
本章介绍了在进行OpenFOAM编程和在HPC集群上使用OpenFOAM时提高生产力的最佳实践。
本节描述了OpenFOAM源代码的组织以及与开发OpenFOAM相关的工作流程。在进行代码开发时,代码应组织为两层:库代码及应用程序代码。库代码可以包含实现各种可重用部件或组件的单个或多个库。这完全取决于库的设计者以及库的构建方式。有时,库级代码被称为应用程序逻辑。库代码在设计上并不特定于单个应用程序:它被许多可执行应用程序重用。库将包含函数或类的声明及其实现。该库通常被编译成所谓的“目标代码”,以节省编译时间。然后,当链接器程序执行库对象代码时,它将链接到应用程序。请注意,虽然库包含已编译代码,但它们不能像可执行应用程序那样在命令行中执行。
另一方面,应用程序代码使用库代码来组装更高级别的功能。OpenFOAM的流动求解器就是一个很好的例子,因为它结合了单独的库来处理概念上不同的任务,如磁盘I/O、网格处理、离散等。求解器的开发者不必关心各个库背后的逻辑,从而可以集中精力开发求解器。
当源代码被组织到应用程序层和库层时,它通常更容易扩展,并且可以更容易地与其他人共享。由于OpenFOAM遵循这种方法,顶级目录$WM_PROJECT_DIR包含两个子目录:applications和src。其中src文件夹存储各种库,而applications文件夹存储使用这些库的可执行应用程序。
在开发过程中,程序员可以选择两种代码组织方式:在OpenFOAM目录结构中编程或在单独的目录结构中编程。乍一看,在OpenFOAM结构中编程很有意义,因为在目录树中保持相似的代码非常接近是合乎逻辑的。然而不幸的是,当使用版本控制系统(VCS)与其他人协作时,这种“主结构”的开发方法会很快导致问题。版本控制系统对于协作编程是绝对必要的。即使开发人员独自工作,VCS也会显著加快开发速度和开发过程的安全性,因为它可以直接调查其他想法。即使版本控制系统使用得当,与其他人共享位于OpenFOAM主存储库中的自定义代码也可能会出现问题,原因如下:
- 对于属于项目的文件没有明确的概述
- 教程和测试用例放在单独的目录结构中
- 处理未与OpenFOAM一起分发的其他依赖项可能会导致变更集成问题
- 与其他人合作需要访问完整的OpenFOAM版本
最后一点使协作工作变得困难,因为创建整个发布存储库的克隆使得任何人都有必要克隆整个OpenFOAM平台,以便在通常更小的新项目上进行协作。此外,还有一些情况是,这些项目没有与公众共享:它们是由公司的研究部门开发的,或者功能还不够成熟,无法发布。在这种情况下,当项目从一开始就不需要与OpenFOAM版本集成时,将库和应用程序代码捆绑在一个单独的存储库中,可以直接编译,这使得个人和协作开发更加容易。在后一点上,当项目证明质量更高时,可以将其集成到其中一个OpenFOAM发布项目中。现在有多种VCS托管服务可用。这些服务提供了高级web界面,允许用户使用bug跟踪、为每个项目托管wiki以及其他工具,这些工具使处理此类项目变得更加容易。其中最受欢迎的有gitlab、github和bitbucket等。
6.1.1 一个新OpenFOAM项目的目录结构
将相同的OpenFOAM组织结构应用于定制的OpenFOAM项目,可以简化协作工作和将来与OpenFOAM的集成。如果代码以这种方式组织,那么对于熟悉OpenFOAM目录结构的用户来说,目录的结构将不言自明。维护统一的目录结构也是间接记录代码的基本方法。要检查示例目录组织,请考虑本书的示例代码存储库及其组织方式。
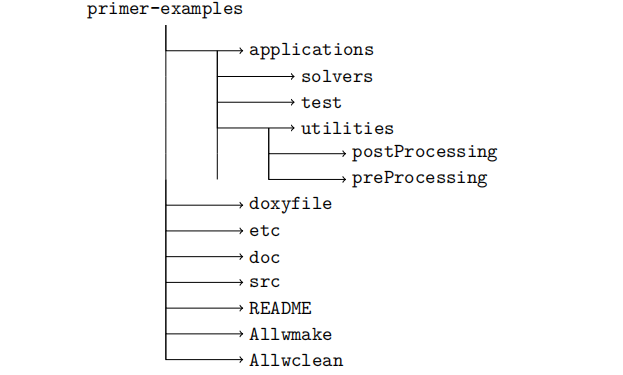
如图6.1所示,application目录是存储应用程序的地方。在application目录中存在以下子目录:solvers、test和utilities。etc目录用于配置代码的编译。每个库的src文件夹的组织结构都不同。当类提取和封装不同抽象之间的常见行为时,分层代码组织也会将不同的类实现集合分离到单独的可链接库中。在引入更改时,组织和分离库类别可以减小已编译应用程序代码的大小,从而加快编译速度。
README文件通常位于代码存储库的顶部目录中,此文件非常有用,因为它是用户开始使用新代码时读取的第一个文件。通常可以在那里找到对项目背景及其最重要应用程序的一般描述,以及到外部文档来源和论坛的最新链接。可以使用Doxygen文档系统生成代码的本地文档,该系统使用doxyfile指定文件以及涉及生成的HTML文档的外观的详细信息。
6.1.2 自动化安装
除了图6.1中的目录组织之外,还应启用简化的自动构建过程。OpenFOAM使用自己的构建系统wmake,该系统利用各种环境变量来自动编译和链接库和应用程序代码。同样的方法可以应用于自定义代码存储库,并针对提供的示例代码存储库实现。示例代码库的bashrc配置脚本如下所示:
#!/bin/sh
DIR="$( cd "$( dirname "${BASH_SOURCE[0]}" )" && pwd )"
export PRIMER_EXAMPLES=${DIR%%/etc*}
export PRIMER_EXAMPLES_SRC=$PRIMER_EXAMPLES/src
export PATH=$PRIMER_EXAMPLES_SRC/scripts:$PATH
bash配置脚本设置名为$PRIMER_EXAMPLES的路径变量,该变量是代码存储库主文件夹的路径变量。PATH变量需要扩展,因为示例代码库包含OpenFOAM中的脚本,这些脚本位于src/scripts中。否则无法从文件系统中的任何位置调用这些脚本。通过对项目路径使用不同的变量,可以在另一个存储库中重用此处的结构和配置。代码存储库的应用程序和库依赖变量$PRIMER_EXAMPLES来查找在编译之前包含的头文件的目录。
根目录中的编译脚本Allwmake和Allwclean分别用于编译和清理项目二进制文件。此外类似的脚本放在src和applications子目录中,这样就可以只编译库或应用程序。用于在src目录中构建库的Allwmake脚本的示例内容如以下脚本所示:
#!/bin/sh
cd ${0%/*} || exit 1 # run from this directory
wmakeLnInclude .
wmake exampleLibrary
在wmakelinclude中,脚本递归搜索当前目录,查找所有OpenFOAM源文件,并在src/lnInclude目录中创建指向这些文件的符号链接。这大大简化了构建过程的配置,因为库的所有头文件都不会分散在不同的子目录中;编译时所需的所有头文件都链接到一个位置lnInclude。一旦定义了存储库文件夹的绝对路径($PRIMER_EXAMPLES由etc/bashrc 脚本定义),包含类声明的头文件就依赖于存储在src/lnInclude目录中的所有源文件的符号链接。要编译的库的名称(在本例中为exampleLibrary)作为一个参数传递给wmake脚本,该脚本确保构建过程将生成一个可动态链接的库。
OpenFOAM的应用程序代码通常存储在以应用程序命名的目录中。示例应用程序目录的内容如图6.2所示。applicationName.C是应用程序的源文件。wmake构建系统使用files和options文件来编译应用程序代码。
文件Make/files中的内容很简单,如下所示:
applicationName.C
EXE = $(FOAM_USER_APPBIN)/applicationName
Make/files文件列出了要编译的C文件以及包含已编译代码的二进制文件的名称和位置。应用程序安装目标目录设置为$FOAM_USER_ APPBIN,以避免自定义应用程序污染OpenFOAM系统应用程序目录$FOAM\U APPBIN。使用$FOAM_USER_APPBIN将二进制文件存储在一个文件夹中,该文件夹是$HOME的子文件夹:这避免了在计算机上构建自定义项目时需要root权限,其中一个OpenFOAM安装可能会在所有具有非root权限的用户之间共享,例如集群。Make/options文件包含包含声明(*.H)文件的所有目录,即所谓的包含目录以及包含库的目录(-L)。options文件内容如下所示:
EXE_INC = \
-I$(LIB_SRC)/finiteVolume/lnInclude \
-I$(LIB_SRC)/meshTools/lnInclude \
-I$(PRIMER_EXAMPLES_SRC)/lnInclude
EXE_LIBS = \
-L$(FOAM_USER_LIBBIN) \
-lfiniteVolume \
-lmeshTools \
-lexampleLibrary
options文件显示,自定义应用程序applicationName依赖于存储库变量$PRIMER_EXAMPLES_SRC和OpenFOAM生成的lnInclude目录来定位所需的头文件。此外,应用程序将链接到库exampleLibrary,并使用其中包含的所需功能。
提示:拥有自定义项目目录结构的关键步骤是准备bashrc配置脚本。依靠该脚本设置的变量来定位自定义项目的头文件和库,将自定义项目与OpenFOAM平台分离。
这种配置是使用自定义代码进行工作和编程的简单方法。以下列表是上述工作流成中步骤的摘要:
- 在终端运行命令
source ./etc/bashrc以设置环境变量$PRIMER_EXAMPLES - 如果要永久设置环境变量,可以将
source/path/to/code/directory/etc/bashrc添加到shell的启动脚本中 - 在顶层代码目录中运行
./Allwmake编译所有的库与应用程序 - 在顶层代码目录中运行
./Allwclean清除所有的二进制文件 - 将库(例如libraryName)添加到存储库时,编辑
src/Allwmake并添加wmake libraryName以进行编译,以及在src/Allwclean中添加wclean libraryName以清理新库代码的二进制文件 - 如果为应用程序使用示例代码存储库中的标准目录,则将在不编辑编译或清理脚本的情况下对其进行编译和清理。
调试的第一个也是最简单的方法是添加Info语句,以缩小代码的细分部分。然而,这种方法最终要比学习如何使用gdb之类的调试器花费更多的时间。代码分析过程通常只应用于功能正常的程序,目的是提高计算效率。
提示:了解如何使用调试器:如果OpenFOAM是并行运行的,那么在不同的MPI进程中没有指定的代码执行顺序,这使得Info语句及其并行对等语句Pout或Perr对调试没有用处。
6.2.1 使用GNU调试器(gdb)进行调试
当OpenFOAM在编译时没有进行任何优化时,使用GNU调试器(gdb)调试代码更为有益。优化由编译器执行,通常不会干扰为已编译代码生成的调试信息。然而,分析和检查编译器未优化的代码可以更深入地了解隐藏的计算瓶颈。
用于OpenFOAM的编译器标志被绑定到多组选项中,这些选项可以根据目标配置进行交换。
编译器选项位于$WM_PROJECT_DIR/etc/bashrc全局配置脚本中,如下所示:
#- Optimised, debug, profiling:
# WM_COMPILE_OPTION = Opt | Debug | Prof
export WM_COMPILE_OPTION=Opt
要使用gdb在调试模式下使用OpenFOAM,必须按以下方式设置$WM_COMPILE_OPTION环境变量:
export WM_COMPILE_OPTION=Debug
为了使此更改生效,必须重新编译OpenFOAM。对于所有需要调试的自定义库和应用程序,也需要重新编译。请记住,使用debug选项编译的代码的执行时间要长得多。
提示:使用gdb进行调试非常简单,官方网站www.gnu.org/software/gdb。
对于诸如segmentation fault(访问错误的内存地址)或floating point exception(除以零)的错误,代码调试可能比较简单。代码执行中的错误触发系统信号,如SIGFPE(浮点异常信号)和SIGSEV(分段冲突信号),并被调试器捕获。然后调试器允许用户浏览代码以查找错误、设置断点、检查变量值等等。
为了显示实际的gdb,本节将介绍使用gdb进行调试的示例。本教程位于ofprimer/applications/test/testDebugging目录下的示例代码库中。
本教程包含一个测试应用程序,其中包含一个函数模板,用于在模拟的所有时间步长上计算给定字段的调和平均值。由于调和平均值涉及计算,其中是变量值,如果代码在包含零值的变量上执行,则会出现浮点异常(SIGFPE)。
函数模板是在fvc::命名空间中定义的,其行为类似于其余的OpenFOAM操作。然而,它的功能确实略有减少。因此,函数模板定义和声明与测试应用程序打包在一起,这不是(也不应该是)标准实践。
可用于此示例的教程模拟案例是ofbook-cases/chapter4/rising-bubble-2D。使用参数-field alpha.water调用testDebugging应用程序。risingBubble-2D案例产生以下错误:
?> testDebugging -field alpha1
(snipped header output)
Time = 0
#0 Foam::error::printStack(Foam::Ostream&) at ??:?
#1 Foam::sigFpe::sigHandler(int) at ??:?
#2 ? in /usr/lib/libpthread.so.0
#3 ? in $FOAM_USER_APPBIN/testDebugging
#4 ? in $FOAM_USER_APPBIN/testDebugging
#5 __libc_start_main in /usr/lib/libc.so.6
#6 ? in $FOAM_USER_APPBIN/testDebugging
Floating point exception (core dumped)
$FOAM_USER_APPBIN变量会扩展到机器上的相应路径。调试此问题的第一步是启动gdb,并结合testDebugging。testDebugging的所有组件都必须在调试模式下编译,这还包括所有感兴趣的库以及OpenFOAM平台。
gdb testDebugging
这将启动gdb的控制台,用于执行任何需要调试的程序:
(gdb)
在gdb的这个调试控制台中,任何命令都可以在run命令的前面执行以进行调试。对于testDebugging应用程序,这意味着alpha1也必须作为附加参数传递:
(gdb) run -field alpha1
执行上述命令后,再次出现SIGFPE错误,但包含更多详细信息:
Program received signal SIGFPE, Arithmetic exception.
0x0000000000414706 in Foam::fvc::harmonicMean<double>
(inputField=...) at testDebugging.C:79
79 resultField[I] = (2. / resultField[I]);
(gdb)
由于OpenFOAM及应用程序在debug模式下编译,gdb直接指向源代码中负责SIGFPE的那一行。对于testDebugging应用程序的最基本示例,手动分析源代码可能会得到相同的见解。随着算法复杂性的增加,手动搜索bug成功的可能性越来越小。虽然插入Info语句是初学者用于调试的第一种方法,但最终它所耗费的时间远远超过学习一些基本gdb命令所需的时间。另一方面,调试器可以:使用存储在内存堆栈上的信息单步执行函数,一次又一次执行循环,更改变量值,在执行中设置断点,根据变量值调整断点,以及调试器文档中提供的许多其他高级选项。
为了使用gdb查看基本工作流,假设上述错误发生在复杂的代码库中。此代码位于具有非内聚类的库中,这些类与跨数百行的fat接口和成员函数强耦合。在这种情况下,程序员需要检查信号线上方和下方的代码,以掌握执行的上下文。调试器可以显示信号的路径:从测试应用程序中的顶级调用,一直到引发此错误的低级容器。通过在gdb控制台中执行frame,可以在gdb中获得此信息:
Program received signal SIGFPE, Arithmetic exception.
0x0000000000414706 in Foam::fvc::harmonicMean<double>
(inputField=...) at testDebugging.C:79
79 resultField[I] = (1. / resultField[I]);
(gdb) frame
#0 0x0000000000414706 in Foam::fvc::harmonicMean<double>
(inputField=...) at testDebugging.C:79
79 resultField[I] = (1. / resultField[I]);
由于testDebugging示例仅包含main函数,因此可以使用单堆栈框架,其中存储了有关函数目标代码的信息。进行多个函数调用时,有多个帧可用。SIGSEV信号的最低帧通常指向基本的OpenFOAM容器UList。然而,错误不太可能是由UList引起的,更可能是由自定义代码引起的。在这种情况下,容器(继承自UList)中的寻址错误是导致错误的原因。
选择frame 0并使用list命令列出源代码,可以缩小错误的位置:
(gdb) frame 0
(gdb) list
75 volumeField& resultField = resultTmp();
76
77 forAll (resultField, I)
78 {
79 // SIGFPE.
80 resultField[I] = (1. / resultField[I]);
因此,SIGFPE信号的罪魁祸首是第80行。要在第80行放置断点,必须执行break命令并重新运行testdebug:
(gdb) break 80
Breakpoint 1 at 0x4146cd: file testDebugging.C, line 80.
(gdb) run
The program being debugged has been started already.
Breakpoint 1, Foam::fvc::harmonicMean<double> (inputField=...) at
testDebugging.C:80
80 resultField[I] = (1. / resultField[I]);
在第80行中放置断点后,可以在此位置计算变量I:
(gdb) print I
$1 = 0
打印resultField[I]显示其值为0。为了检查resultField[I]的不同值的影响,可以使用gdb手动设置它们:
(gdb) set resultField[I]=1
(gdb) c
Continuing.
Breakpoint 1,
Foam::fvc::harmonicMean<double> (inputField=...)
at testDebugging.C:80
80resultField[I] = (1. / resultField[I]);
(gdb) c
Continuing.
Program received signal SIGFPE, Arithmetic exception.
0x0000000000414706 in
Foam::fvc::harmonicMean<double> (inputField=...)
at testDebugging.C:80
80 resultField[I] = (1. / resultField[I]);
(gdb) print I
$2 = 1
(gdb)
对于这个简单的示例,很明显,对于resultField,至少有两个I值会导致0。根据定义,字段resultField永远不能为0,因此下一步是调查变量是否已正确预处理。
提示:此示例的源代码中已经包含了问题的解决方案-取消对标记行的注释可以使应用程序正确运行。
6.2.2 代码分析
使用性能度量的代码分析对于CFD软件至关重要,因为CFD软件不仅必须准确、健壮,而且在单个CPU核上必须快速,对于大型问题,在多个CPU核上运行时必须快速。
使用valgrind评测应用程序评测代码相对简单。valgrind允许开发人员发现代码中的计算瓶颈,并使用调用图和类似图以图形方式显示它们。在优化代码以提高效率时,可以使用这些信息更有效地集中精力。通常,使用估计的90-10或80-20规则分布性能,这意味着90(80%)的计算通常由10(20%)的代码执行。
与前面关于使用gdb进行调试的部分类似,代码需要使用调试编译选项进行编译。优化的高级形式与软件设计直接相关:适当地选择算法和数据结构。一旦有效地选择了算法和数据结构,就有可能执行所谓的低级优化(例如循环展开)。
复杂性是用来计算算法和数据结构效率的参数。用大写字母“O”表示:例如:,其中n表示操作的元素数量。当有一种复杂度较低的替代算法可用时,通常不建议深入研究低级优化。这同样适用于数据结构选择:仔细选择数据结构是绝对必要的。有关容器结构的更多信息,可以从C++数据结构文档中的标准模板库(STL)中获得(有关详细信息,请参见Josuttis[1])。OpenFOAM容器不是基于STL的(尽管其中一些容器提供STL编译器迭代器接口),但它们的功能非常相似,例如:
DynamicList类似于std::vector。如果容器大小小于其容量,则两者都可以直接访问具有复杂性和插入复杂性的元素。如果插入操作产生的大小大于当前容量,则插入复杂性将与成比例(见[2])。
DLList与std::list类似,插入复杂性(容器中的任何位置)为,访问复杂性为。
OpenFOAM中的许多算法工作都与非结构化有限体积网格的特定owner-neighbour寻址有关,具有算法代码自动并行的优点。对于标准OpenFOAM库代码,数据结构的选择介于四个主要容器族之间:
- List
- DynamicList
- 链表
*LList* - 作为哈希表实现的关联映射
在为特定算法选择容器之前,必须事先检查容器接口。否则,所选容器可能无法正确满足算法的需要,导致执行时间更长。
示例应用程序testProfiling可以使用一个非常简单的示例来说明DynamicField容器的这一点。尝试在系统上的任何位置执行评测测试应用程序(它不需要在OpenFOAM simulation案例目录中执行):
?> testProfiling -containerSize 1000000
传递给testProfiling测试应用程序的-containerSize选项设置附加到两个不同DynamicField对象的元素数:第一个对象初始化为null,第二个对象初始化为与传递给应用程序的整数值对应的大小。对于在DynamicField末尾追加元素的代码部分,已将计时代码添加到应用程序中。您可以执行为容器大小提供不同值的应用程序,并查看初始化容器和具有初始化大小的容器之间的时间差异。作为DynamicList容器,如果插入后容器的大小小于初始容器容量,则DynamicField在容器末尾插入元素时具有恒定的复杂性,否则在末尾插入(附加)操作的复杂性与容器大小成线性关系。这意味着,如果容器的大小很大,那么它将对代码的效率产生更大的影响;如果容器存储复杂的对象,那么会增加不必要的n−1附加在容器末端的每个元素的构造。
在调试模式下构建示例源代码存储库后,可以使用valgrind评测testProfiling应用程序:
?> valgrind --tool=callgrind testProfiling -containerSize 1000000
Valgrind可以使用各种工具,如捕捉缓存未命中、检查程序是否存在内存泄漏等,但这超出了本书的范围。有关这些主题的更多信息,请参阅valgrind官方文档。
执行上述命令将生成一个名为callgrind.out.ID的文件,其中ID是进程标识号。输出文件可以使用kcachegrind打开,kcachegrind是一个开源应用程序,用于可视化valgrind的输出。正如您可能在testProfiling应用程序生成的计时输出中所注意到的,valigrind显示,大约62%的总执行时间用于将元素附加到未初始化的DynamicField对象,大约14%用于将元素附加到预初始化的DynamicField对象。
这使我们得出结论,尽管DynamicList和DynamicField是动态的,但一旦超出容量,在这样的容器的末端附加元素是需要付出代价的。如果我们的算法不需要直接访问元素,如果它一个接一个地循环元素,那么使用基于堆的链表可能是更好的选择。然而,分配非顺序内存块和指针间接寻址也会占用CPU周期,因此很难事先知道容器的正确选择。这个问题的答案是以泛型编程的形式出现的,以一种仔细而周到的方式将算法与容器分离(这并不总是可能的),并分析代码。
Git是一种分布式VCS,在开源社区非常流行。使用git有很多好处:创建新版本非常简单,这简化了尝试新想法的过程,git web服务(GitLab、GitHub、Bitbucket)简化了处理由多个贡献者编辑的文件中的冲突,每个贡献者都持有项目的完整副本,贡献者可以在不访问internet的情况下工作,因为工作时不需要与中央存储库建立开放连接等。git上有大量的在线信息1。在剩下的章节中,我们假设对git有一个合理的理解。要使用OpenFOAM,只需了解如何:克隆远程存储库,在本地和远程存储库上创建删除和合并版本(分支),从远程存储库推送和拉取,以及创建项目的git标记(快照)。在envie.com上可以找到一个很好的分支模型。下面我们将概述一些涉及git和OpenFOAM的用例。
提示:虽然这里没有介绍,但学习git版本控制系统的基本用法对于OpenFOAM开发是必要的。
OpenFOAM git存储库位于https://develop.openfoam.com/Development/openfoam/,可以通过下面的命令访问:
git clone https://develop.openfoam.com/Development/openfoam.git
命令完成后,整个历史记录在本地计算机上可用,并且可以调查发布的历史记录。存储库在主(主)分支中克隆。OpenFOAM快照(版本)定期创建为git标记
?> openfoam
?> git tag
OpenFOAM-v1601
OpenFOAM-v1606
OpenFOAM-v1612
OpenFOAM-v1706
OpenFOAM-v1712
OpenFOAM-v1806
OpenFOAM-v1812
OpenFOAM-v1812.200312
OpenFOAM-v1812.200417
OpenFOAM-v1906
OpenFOAM-v1906.191111
OpenFOAM-v1906.200312
OpenFOAM-v1906.200417
OpenFOAM-v1912
OpenFOAM-v1912.200129
OpenFOAM-v1912.200312
OpenFOAM-v1912.200403
OpenFOAM-v1912.200417
OpenFOAM-v1912.200506
OpenFOAM-v1912.200626
OpenFOAM-v2006
可以使用下面的命令签出发布标签:
git checkout OpenFOAM-v2006
历史记录或日志提供有关更改的信息:作者、日期和描述更改的消息(git提交)。
git log
主动开发的功能可作为功能分支使用:
?> git branch -a
remotes/origin/cloud-function-objects-extension
remotes/origin/code-review.mol
remotes/origin/code-review.saf
remotes/origin/develop
remotes/origin/doc-utilities.kbc
remotes/origin/feature-GIS-tools
remotes/origin/feature-MPPIC-dynamicMesh
remotes/origin/feature-PatchFunction1-ACMI
remotes/origin/feature-dlLibrary-unloader
remotes/origin/feature-film-flux-function-object
remotes/origin/feature-generalizedNewtonian
remotes/origin/feature-generalizedNewtonian.orig
remotes/origin/feature-generalizedNewtonian.up1
remotes/origin/feature-liquidFilm
...
如果你决定直接在OpenFOAM的主要结构中工作,在develop.openfoam.com上创建一个帐户,从项目维护人员中请求成为该项目成员,然后fork OpenFOAM。一旦功能被彻底测试,就可以提交一个合并请求,这样代码就可以集成到OpenFOAM中。
1、将独立的OpenFOAM项目置于版本控制下
使用git进行定制开发的最常见方法是在与主版本无关的单独存储库中跟踪每个项目。这简化了代码的共享,因为它可以在没有完整OpenFOAM版本的情况下共享。假设三个项目应置于版本控制之下:projectA、projectB和projectC。必须单独输入这些项目的每个目录,并且必须在每个目录中初始化git存储库:
cd projectA
git init
这些存储库中的每一个都是本地的并且是空的。必须手动将文件添加到存储库中。以防止在编译时生成的.deb文件和lnInclude目录污染存储库。还应添加gitignore文件,以防止它们出现在存储库中。此方法使您能够更轻松地在不同的OpenFOAM版本之间共享和移植代码。
2、在主存储库中开发
虽然一开始直接在OpenFOAM存储库中开发可能有点奇怪,但与将开发放在单独的存储库中相比,它有几个优点。如果管理一个HPC集群并为所有应该使用一些自定义开发的用户安装一个全局OpenFOAM版本,那么这种开发方式可能会派上用场。合并主分支并只对该分支应用更改是将自定义开发集成到OpenFOAM存储库中的一种相当安全的方法。然后将此分支部署到HPC集群。
主分支应该与主存储库的主存储库类似,主存储库的任何上游更改都应该合并到本地开发分支中,以保持最新。使用git挂钩,部署本身可以进一步自动化。然而,在这种配置中,将开发从一个主要版本迁移到下一个版本可能比使用独立的存储库更加困难。
3、模拟案例的版本控制
因为git可以跟踪任何文本文件,所以它不仅限于源代码,还可以处理OpenFOAM的情况。一些文件和目录,如时间步长和处理器目录,不应该被git跟踪,因此必须被适当的.gitignore文件排除。这个选择已经由.gitignore在ofbookcases项目中完成了,它会忽略网格和许多其他与案例设置没有直接关系的文件和目录。跟踪案例的一个很好的应用是研究各种参数对模拟的影响。这使得多次复制相同的案例变得过时。出版物或技术报告中使用的模拟案例版本的快照可以使用git标记创建。
提示:与HPC群集的系统管理员联系,以确保正确构建OpenFOAM。
在本节中,当尝试在HPC集群上安装OpenFOAM时,将考虑一些主题。在远程集群上工作时,需要一个由不同硬件、软件库和编译器版本组成的全新系统。由于这些差异,每个系统都会有所不同,安装时可能会遇到特殊的挑战。
尽管如此,本节将尝试概述您在任何特定系统上可能遇到的一些更通用的问题,而不是涵盖系统细节。接下,假设读者在执行编译器、设置其配置以及使用Linux系统环境变量方面有一定的经验。这包括将包含文件夹和库二进制文件链接到编译。
- 修改
$WM_PROJECT_DIR/etc/bashrc文件更改编译器
# [WM_COMPILER_TYPE] - Compiler location:
# = system | ThirdParty
export WM_COMPILER_TYPE=system
# [WM_COMPILER] - Compiler:
# = Gcc | Gcc4[8-9] | Gcc5[1-5] | Gcc6[1-5] | Gcc7[1-4] | Gcc8[12] |
# Clang | Clang3[7-9] | Clang[4-6]0 | Icc | Cray | Arm | Pgi
export WM_COMPILER=Gcc
建议使用HPC集群上可用的MPI库,因为它们是由集群管理员精心构建的,以最大限度地提高特定计算机上的性能。如果使用OpenFOAM打包的库存第三方文件夹中包含的OpenMPI库进行编译,求解器可能仍能正常工作,但没有相当多的并行优化和互连支持。这可能会严重阻碍并行速度和伸缩性,不建议这样做。
如果没有功能齐全的MPI编译,OpenFOAM的Pstream库将无法正确编译。Pstream库充当CFD库和原始MPI函数之间的接口,这对于任何并行计算都是必要的。
每个集群通常都有一个官方支持的编译器用于系统。这可能是一个开源编译器,如Gcc,但也可能是一个预配置的商用C++编译器,如Intel®提供的Icc。要为OpenFOAM选择编译器,必须调整主配置文件$WM_PROJECT_ DIR/etc/bashrc。文件中涉及编译器选择的部分如清单所示。第一个选项,编译器位置,定义wmake在任何编译活动中是使用系统编译器还是使用与OpenFOAM一起打包在第三方目录中的编译器。在HPC安装的情况下,应始终使用系统编译器。另一个选项将设置要使用的编译器。有很多选项可用,但它们可能都没有安装在相关系统上。例如,许多基于Linux的计算集群将在系统的某处安装Gcc,但推荐的编译器可能是经过高度优化和调优的Icc版本。在这种情况下,编译器应定义为:
# [WM_COMPILER] - Compiler:
# [WM_MPLIB] - MPI implementation:
# = SYSTEMOPENMPI | OPENMPI | SYSTEMMPI | MPI | MPICH | MPICH-GM |
# HPMPI | CRAY-MPICH | FJMPI | QSMPI | SGIMPI | INTELMPI | USERMPI
# Also possible to use INTELMPI-xyz etc and define your own wmake rule
export WM_MPLIB=SYSTEMOPENMPI
# = Gcc | Gcc4[8-9] | Gcc5[1-5] | Gcc6[1-5] | Gcc7[1-4] | Gcc8[12] |
# Clang | Clang3[7-9] | Clang[4-6]0 | Icc | Cray | Arm | Pgi
export WM_COMPILER=Icc
与编译器一样,需要将wmake配置为针对特定于HPC系统的受支持MPI实现进行构建。这是在与编译器选择相同的bashrc文件中完成的(请参见清单3)。根据选择的实现,OpenFOAM为 MPI_ARCH_PATH and MPI_HOME设置不同的目标位置,该位置是集群文件系统中存在这些MPI可执行文件、库和头文件的位置。HPC安装中最常见的问题之一是,由于缺少MPI库和标头,此目录未正确设置,并且Pstream库未正确编译。
在这种情况下,WM_MPILIB=OPENMPI设置将指示我们使用与ThirdParty目录打包的OPENMPI版本。如果改为设置SYSTEMOPENMPI,脚本将查找系统以加载OpenMPI库。根据选择定义这些环境变量的脚本位于MPI_HOME _foamAddPath MPI_ARCH_PATH/bin
如果hpmpi文件夹的位置不完全是/opt/hpmpi,则将无法正确设置MPI\U HOME,错误将在整个脚本中层叠,并最终中断编译。谢天谢地,假设目标MPI实现在系统目录树中的位置已知,手动设置这些变量非常容易。
```bash
source ~/OpenFOAM/OpenFOAM-2.2.0/etc/bashrc
export MPI_ARCH_PATH=/opt/apps/ssmpi/1.3
export MPI_HOME=/opt/apps/ssmpi/1.3
wmake规则如下所示:
?> cat WM_PROJECT_DIR/wmake/General/mplibOPENMPI
PFLAGS = -DOMPI_SKIP_MPICXX
PINC = -I<span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right:0.13889em;">MP</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.07847em;">I</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3283em;"><span style="top:-2.55em;margin-left:-0.0785em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">A</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord mathnormal" style="margin-right:0.07153em;">RC</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.08125em;">H</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3283em;"><span style="top:-2.55em;margin-left:-0.0813em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right:0.13889em;">P</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord mathnormal">A</span><span class="mord mathnormal" style="margin-right:0.13889em;">T</span><span class="mord mathnormal" style="margin-right:0.08125em;">H</span><span class="mclose">)</span><span class="mord">/</span><span class="mord mathnormal">in</span><span class="mord mathnormal">c</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">u</span><span class="mord mathnormal">d</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mord mathnormal">L</span><span class="mord mathnormal" style="margin-right:0.07847em;">I</span><span class="mord mathnormal" style="margin-right:0.05764em;">BS</span><span class="mspace" style="margin-right:0.2778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right:0.2778em;"></span></span><span class="base"><span class="strut" style="height:0.7667em;vertical-align:-0.0833em;"></span><span class="mord">−</span><span class="mord mathnormal">L</span></span></span></span>(MPI_ARCH_PATH)/lib<span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mopen">(</span><span class="mord mathnormal" style="margin-right:0.13889em;">W</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3283em;"><span style="top:-2.55em;margin-left:-0.109em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right:0.07153em;">C</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord mathnormal" style="margin-right:0.13889em;">OMP</span><span class="mord mathnormal" style="margin-right:0.07847em;">I</span><span class="mord mathnormal">L</span><span class="mord mathnormal" style="margin-right:0.05764em;">E</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.00773em;">R</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3283em;"><span style="top:-2.55em;margin-left:-0.0077em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">L</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord mathnormal" style="margin-right:0.07847em;">I</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.05017em;">B</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3283em;"><span style="top:-2.55em;margin-left:-0.0502em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight">A</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord mathnormal" style="margin-right:0.07153em;">RC</span><span class="mord mathnormal" style="margin-right:0.08125em;">H</span><span class="mclose">)</span><span class="mspace" style="margin-right:0.2222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right:0.2222em;"></span></span><span class="base"><span class="strut" style="height:0.6833em;"></span><span class="mord mathnormal">L</span></span></span></span>(MPI_ARCH_PATH)/lib -lmpi
假设这个集群支持一个特定的、虚构的MPI实现,称为超级伸缩MPI,简称ssmpi。这个虚构的库版本为1.3,可以在目录树/opt/apps/ssmpi/1.3中找到。
由于脚本不知道如何配置wmake以链接到此,因此必须在$HOME/.bashrc中手动定义mpi环境变量。在获取OpenFOAM bashrc后,相应地设置变量,以确保覆盖任何加载错误的值。在查看用于设置MPI编译器标志的wmake规则时,设置此环境变量的重要性显而易见(请参见清单5)。在使用OpenMPI编译的配置文件中,这些变量用于设置指向标头和二进制位置的路径。如果安装是用虚构的SSMPI代码设置的,则将按照此命名约定创建一个新的配置文件,并用适当的文件路径填充。最后,所有这些设置都是为了确保Pstream库正确编译并链接到本地MPI实现。Pstream编译选项存储在$WM_PROJECT_DIR/src/Pstream/mpi/Make/options中,包含PFLAGS、PINC和PLIB,它们通过-I和-L直接提供给编译器标志。这将在编译时用于头和库链接。除了与MPI库接口之外,OpenFOAM大部分是自包含的,只有少数其他外部库依赖。如果在编译期间发生重大故障,则很可能在配置这些MPI库和编译器设置期间发生。
- Nicolai M. Josuttis. The C++ standard library: a tutorial and reference. Boston, MA, USA: Addison-Wesley Longman Publishing Co., Inc., 1999.
- Why is std::vector:: insert complexity linear (instead of being constant)? Url: http://stackoverflow.com/questions/25218880/Why-is-stdvectorinsert-complexity-linear-instead-of-being-constant (visited on 03/2016).
本章介绍了在OpenFOAM中对湍流的建模。物理和数学建模的细节保持在最低限度。
做出这一决定的原因在于,湍流建模本身就是一个很大的主题,超出了本书的范围。对于湍流模型的更深入的讨论,读者可以参考各自的文献,如Pope [11], Pozrikidis [12], Wilcox[16]和Lesieur[8]。
通常,有四种不同的方法来模拟湍流及其影响。湍流模型的主要目的是确定雷诺应力,因为它们在动量方程中是未知的(见第1章)。
根据模型类型,计算雷诺应力的方法可能会从相对简单到非常复杂不等,这反过来又会导致对所需计算工作量和计算网格的不同要求。图7.1简要概述了这些模型。
湍流模型最基本的类别是雷诺平均Navier-Stokes(雷诺平均Navier-Stokes(RANS))模型,因为该组的所有模型都研究平均速度的时间波动,即雷诺平均(见[13,8])。这种类型的模型可以在相对粗糙的网格上工作,因为湍流波动不是几何上解决的,而是模拟的。如果从字面上看,这些模型只适用于稳态模拟,因为无法模拟真实的湍流波动。这种RANS模型的突出例子是k-epsilon模型(见[5,6])、k-ω模型(见[15])和k-ω-SST模型(见[9,10])。OpenFOAM中这些模型的实现位于Reynolds Averaged Simulation(RAS)模型库中。
下一组模型称为大涡模拟(Large Eddy Simulation,LES),与其中只有小规模涡模拟的RANS模型不同。大尺度涡由计算网格在空间上解析,与RANS模型相比,需要更精细才能正确运行。在计算成本和效率方面,LES位于RANS和直接数值模拟(DNS)之间,如图7.1所示。Pope[11]指出,“对于大尺度显著不稳定的流动,LES在预期上可以比雷诺应力模型更准确和可靠”。
DNS基于求解所有流量尺度的Navier-Stokes方程,并且不部署任何湍流模型。实施这种方法是最简单的方法,但由于所有空间和时间尺度都需要完全解析,所需的计算量非常高。
OpenFOAM中的湍流建模是通用的,因此可以在每个求解器中选择任何模型。这当然假设求解器支持湍流建模,这是大多数求解器的情况。当应该使用不同的湍流模型时,通用实现的主要优点是能够将RTS与湍流模型结合使用并且不必重新编译求解器。所有湍流模型都可以在$FOAM_SRC/TurbulenceModels中找到,它们各自的实现在可压缩、不可压缩和LES型模型之间变化。在下文中,仅涵盖RANS模型的一小部分,而LES,分离涡流模拟(DES)和DNS模型被忽略。
7.1.1 壁面函数
“在高雷诺数下,边界层的粘性子层非常薄,难以使用足够的网格来求解”(见[3])。壁面函数依赖于壁面通用定律,该定律指出,几乎所有湍流的壁面附近的速度分布都是相似的。
当判断壁函数的适用性时,最突出的参数之一是无量纲壁面距离,由Schlichting和Gersten[14]定义为: 其中表示与壁的绝对距离,和分别表示摩擦速度和运动粘度。
Pope[11]对壁面函数以及为什么它们如此重要提供了深刻的见解。湍流模型需要考虑壁面和相对靠近壁面的陡峭的速度分布。这就是壁面函数发挥作用的地方,这是由Launder和Spalding首先提出的。其思想是在距离壁面一定距离处应用附加边界条件,以满足对数定律。因此,湍流模型引入的附加方程无法在靠近壁面处求解。根据使用的特定湍流模型,不同的壁面函数必须应用于湍流模型的各个物理场。意思是k− epsilon模型需要不同于k-w的壁面函数。
警告:特别是当流动遭受严重的流动分离时,RANS模型通常无法正确捕获这种分离。因此,如果使用RANS模型(参见Pope[11],Wilcox[15]以及Ferziger和Perić[3]),必须小心处理这些流动问题。
不同的湍流模型及其相关的壁面函数需要不同的 y+ 值,因此需要不同的近壁面区域的空间分辨率。读者可参考特定文献,了解靠近壁面的计算网格必须达到的所需 y+ 值。请注意,如果对数律区域通过网格进行几何解析,则无需应用壁面函数。根据模拟的类型,如此低的 y+ 值要么在网格划分过程中极难达到,要么甚至是不可取的,因为这显著降低了时间步长。
在 OpenFOAM 中,壁面函数只不过是应用于wall类型边界的patch的普通边界条件。如果将壁面函数边界条件应用于patch边界类型,则求解器将在运行时弹出错误消息。由于壁面函数在实现方面与边界条件非常相似,因此本章不明确讨论它们的设计。第 10 章详细讨论了边界条件。
根据选择的湍流模型,有新的物理场被引入到仿真中,这些物理场也需要求解。为了简单起见,以k−ω湍流模型为例。基本上有两种类型的边界条件可用于模拟边界处的湍流模型的参数:标准条件和湍流特定条件。
1、标准边界条件
如果用户知道特定的流入值,则可以使用标准边界条件,例如fixedValue或inletOutlet边界条件。这些值,即湍流动能 k 和特定耗散率 ω 可以根据湍流强度 I 或混合长度 L 手动计算(参见 [4]):
这里湍流强度应选择为,对于自由流,I = 0.05 是常见的选择。假设流入边界处的湍流粘度比 非常低,通常选择为 ,正如 Fluent [4] 所讨论的那样。当混合长度已知时,通常使用公式(7.4),而公式(7.3)可以直接用于其他情况。当这些值被确定时,它们可以简单地分配给各自的边界。
2、湍流指定边界条件
在某些情况下可以使用湍流特定的边界条件,这反过来又实现了上述一些方程,然后可以将其用于流入的初始化。这些特殊流入边界条件中的第一个是 turbulentIntensityKineticEnergyInlet,它根据方程 (7.2) 初始化 。将此边界条件应用于边界 INLET,会得下面的代码。
INLET
{
type turbulentIntensityKineticEnergyInlet;
I 0.05;
}
此外,可以使用 turbulentMixingLengthFrequencyInletFvPatchScalarField 直接定义基于湍流混合长度初始化(方程(7.4))的 ω 入口。与 turbulentIntensityKineticEnergyInlet 类似,此边界条件只需要一些附加参数,然后根据方程 (7.4) 计算 ω。这里列出了名为INLET的边界所需的字典,Cμ直接从选定的湍流模型中读取,不需要再次指定。
INLET
{
type turbulentMixingLengthFrequencyInlet;
L 0.005;
}
对于其他湍流模型引入的其他领域,OpenFOAM 框架中包含等效的边界条件。
7.2.1 预处理
其他一些有用的预处理应用程序包括 boxTurb 和 applyBoundaryLayer。 boxTurb 可用于初始化非均匀且出现湍流的速度场,这对于湍流效应起主要作用且必须从模拟开始时就存在的情况很方便。得到的速度场仍然满足连续性方程,因此散度为零。
使用 applyBoundaryLayer 可以简化近壁流的开发并提高其收敛性。它根据 1/7 次幂律计算边界层(参见 [4, 2]),并相应地调整速度场。
此工具提供了两个自定义命令行参数 Cbl。 Cbl 将边界层厚度计算为其参数和到壁面的平均距离的乘积。可选地,湍流粘度场 可以存储到磁盘,湍流模型不要求存在该物理场。
7.2.2 后处理
结合前面描述的预处理工具,在OpenFOAM中有各种各样的后处理应用。在每次使用湍流模型的模拟之后,需要检查 y+ 值。为此,有 yPlusRAS和 yPlusLES。它们分别可以用于RANS或LES模拟。它们的工作原理非常相似,不再赘述。要计算特定的 y+ 值,必须在有问题的模拟案例中调用相应的命令。默认情况下,为案例的每个可用时间目录计算 y+。可以通过传递带有适当参数的 -times 参数或简单的 -latestTime 选项来将其限制为特定的类型。
(缩短的)输出如下所示:
?> simpleFoam -postProcess -func yPlus -latestTime
Reading field p
Reading field U
Reading/calculating face flux field phi
Selecting incompressible transport model Newtonian
Selecting turbulence model type RAS
Selecting RAS turbulence model kOmegaSST
Selecting patchDistMethod meshWave
[...]
No finite volume options present
yPlus yPlus write:
writing field yPlus
patch FOIL y+ : min = 62.8783, max = 151.871, average = 122.018
从上面的列表可以看出,wall类型的边界的最小、最大和平均 y+ 值被打印到屏幕上。
有时,为了后处理的目的,必须计算雷诺应力 并将其写入物理场。命令行工具 R 专门为此而定制,不需要额外的参数,并以与 yPlus 后处理函数类似的方式执行,如图所示。
simpleFoam -postProcess -func R -latestTime
湍流模型的设计与输运模型类的设计非常相似,因此在本节中不再赘述。第 11 章介绍了传输模型。模型不仅可以直接访问单个湍流模型,还可以嵌套到子类中。因此,湍流模型的子类以及每个单独的湍流模型都可以使用运行时选择 (RTS) 进行选择。这产生了 RASModel 和 LESModel 类型的子类,它们中的每一个都包含单独的模型实现。
- H.D. Baehr and K. Stephan. Heat and Mass Transfer. Springer, 2011.
- Lawrence J. De Chant. “The venerable 1/7 th power law turbulent velocity profile: a classical nonlinear boundary value problem Solution and its relationship to stochastic processes”. In: Applied Mathematics and Computation 161.2 (2005), pp. 463–474.
- J. H. Ferziger and M. Perić. Computational Methods for Fluid Dynamics. 3 rd rev. Ed. Berlin: Springer, 2002.
- Fluent. Fluent 6.2 User Guide. Fluent Inc. Centerra Resource Park, 10 Cavendish Court, Lebanon, NH 03766, USA, 2005.
- W.P Jones and B.E Launder. “The prediction of laminarization with a two-equation model of turbulence”. In: International Journal of Heat and Mass Transfer 15.2 (1972), pp. 301–314.
- B.E. Launder and B.I. Sharma. “Application of the energy-dissipation model of turbulence to the calculation of flow near a spinning Disc”. In: Letters in Heat and Mass Transfer 1.2 (1974), pp. 131–137.
- B.E. Launder and D.B. Spalding. Mathematical Models of Turbulence. Academic Press, 1972.
- M. Lesieur. Turbulence in Fluids. Fluid Mechanics and Its Applications. Springer, 2008.
- F. R. Menter. “Zonal two-equation k − ω turbulence models for aerodynamic flows”. In: AIAA Journal (1993), p. 2906.
- F. R. Menter. “Two-equation eddy-viscosity turbulence models for engineering applications”. In: AIAA Journal 32.8 (1994), pp. 1598–1605.
- S. Pope. Turbulent Flows. Cambridge University Press, 2000.
- C. Pozrikidis. Introduction to Theoretical and Computational Fluid Dynamics. 2 nd ed. Oxford University Press, 2011.
- O. Reynolds. “On the Dynamical Theory of Incompressible Viscous Fluids and the Determination of the Criterion”. In: Philosophical Transactions of the Royal Society of London. A 186 (1895), pp. 123–164.
- Hermann Schlichting and Klaus Gersten. Boundary-Layer Theory. 8 rd rev. Ed. Berlin: Springer, 2001.
- D. C. Wilcox. “Re-assessment of the scale-determining equation for advanced turbulence models”. In: American Institute of Aeronautics and Astronautics Journal 26 (1988).
- D. C. Wilcox. Turbulence Modeling for CFD. D C W Industries, 1998.
有许多方法可以对 OpenFOAM 进行前处理和后处理,编程新的求解器应用程序或数值算法可能需要用户开发新的预处理和后处理应用程序
在考虑开发新的预处理或后处理应用程序之前,应该确保所需的算法在OpenFOAM中不可用。例如,作为 swak4foamproject 的一部分,Bernhard Gschaider 开发了一个用户友好的预处理应用程序 funkySetFields。此应用程序可用于使用代数表达式初始化 OpenFOAM 物理场。 funkySetFields 中的表达式解析器从用户定义的表达式中提取算术和微分运算,并使用 OpenFOAM 数值库对其进行计算。如果所需的功能在 OpenFOAM、其任何子模块或相关项目中不可用,则使用新功能扩展现有应用程序或库可能比从头开始编程和测试新应用程序更简单。
在这种情况下,一个好的做法是找到具有类似功能的现有应用程序并对其进行修改以适应所需的任务。如第 6 章所述,Doxygen 生成的 HTML 文档可以帮助识别和定位 OpenFOAM 框架中可用于构建新应用程序的那些部分。
可以使用一组 Linux shell 脚本来帮助创建“骨架”源代码文件:应用程序、类、类模板和构建文件(由 wmake 构建系统使用)。创建简单的预处理或后处理应用程序时,只需要一个源代码文件(例如 myApp.C)。遵循 OpenFOAM 命名约定,它存储在以与应用程序相同的方式命名的目录中。
要从头开始编写新应用程序,可以使用如下所示的foamNewApp 脚本。
?> foamNewApp myApp
Creating application code directory myApp
Creating Make subdirectory
foamNewApp 实用程序将在 Make/files 文件中将存储已编译二进制文件的目标位置设置为 (LIB_SRC)/finiteVolume/lnInclude
如果 -I 选项不使用文件夹的相对路径,则会使用环境变量,例如上例中的 $(LIB_SRC)。此外,定义了包含与应用程序链接的预编译动态库的目录列表。
包含库的目录使用选项 `-L `附加到构建选项中:
```bash
-L$(LIBRARY_VARIABLE)/lib
在此示例中,LIBRARY_VARIABLE 是一个环境变量,用于存储包 lib 文件夹的路径。这是存储可加载库二进制文件的位置。当应用程序由其他库组成时,Make/options 文件需要列出要链接的库:
-lusedLibrary
这里 usedLibrary 库将在运行时链接到以前编译的应用程序。
上述步骤是特定于应用程序的,因此将在以下部分中对其进行更详细的描述。有关库、链接和构建过程的更多信息,可以在任何有关 Linux 环境和 Internet 中的编程的书籍中找到。
自定义前处理应用程序可能涉及以 OpenFOAM 中尚不可用的方式准备初始条件、准备在 HPC 集群上执行并行模拟或设置参数变化。在本节中,我们关注并行执行和参数变化。
使用通过 shell 或基于 Python 的脚本链接在一起的各种应用程序,通常可以执行和自动化数量惊人的任务。 OpenFOAM 的良好做法是在模拟案例文件夹中准备一个所谓的 Allrun 脚本,该脚本执行准备模拟所需的预处理脚本。
本节介绍了两个具有不同复杂性的示例。在第一个示例中,一个简单的 shell 脚本使用现有的预处理应用程序调用 OpenFOAM 可执行文件。第二个示例涵盖使用 PyFoam 库对预处理应用程序进行编程以生成参数变化。 Bernhard Gschaider 主要开发 PyFoam 项目:一组用 Python 编程语言编写的库和可执行程序,用于直接参数化和分析 OpenFOAM 模拟。
8.2.1 并行应用程序执行
考虑大量模拟需要使用高性能集群的情况。对于这个例子,所有的模拟案例将被分解成不同的子域,并存储在一个名为 Simulations 的目录中。模拟目录将作为 $FOAM_RUN 目录的子目录放置。与其手动启动每个模拟,不如尽可能自动化此过程。为此,可以使用以下步骤对 shell 脚本进行编程:
- 从 controlDict 检索求解器名称
- 从 decomposeParDict 中检索子域的数量。
- 使用正确数量的处理器执行 mpirun 命令。
在此示例中,脚本名为 Allparrun,并存储在模拟目录中。作为第一步,应该在脚本的开头添加几行。在随 OpenFOAM 发布的大部分教程中都可以找到类似的代码:
#!/bin/bash
cd ${0%/*} || exit 1
source $WM_PROJECT_DIR/bin/tools/RunFunctions
application=getApplication
getApplication 函数是 OpenFOAM 中现有的 bash 函数,非常适合本示例,因为在本例中,应用程序的名称将是求解器的名称。
接下来,必须找到simulation目录中的所有案例子目录。假设这些目录都是正确的 OpenFOAM 模拟案例。因此,OpenFOAM 模拟将在模拟目录的每个子目录中启动。 find 命令用于专门查找可在 $FOAM_RUN/simulations 中找到的目录(参见清单 9)。上述行查找直接(非递归)位于 $FOAM_RUN 目录中的任何目录,以便稍后可以对这些情况中的每一个执行相同的操作。 find 命令可以很容易地通过例如使用通配符过滤某些目录名称,但为了简单起见,在此示例中假设模拟目录仅包含 OpenFOAM 案例。
for d in `find $FOAM_RUN/simulations -type d -maxdepth 1`
do
# This part will be programmed at a later point in this section.
done
下一步是从 system/controlDict 检索子域的数量并将其存储在变量中以供以后使用。为此,在 Allparrun 脚本中引入了一个名为 nProcs 的新函数,该函数返回子域的数量:
function nProcs
{
n=`grep "numberOfSubdomains" system/decomposeParDict \
| sed "s/numberOfSubdomains\s//g" \
| sed "s/;//g"`
echo $n
}
该函数调用 grep 程序来过滤 system/decomposeParDict 中包含 numberOfSubdomains 的行。在这一行中,“numberOfSubdomains”字符串被删除,该关键字和实际数值之间的任何空格都被删除,并且尾分号被删除。此链接命令的结果存储在 bash 变量 n 中。要返回它,使用 echo 。
使用 mpirun 命令并行运行任何 OpenFOAM 求解器或实用程序。对于此示例,这意味着需要将两个变量作为选项参数传递给 mpirun:求解器名称和处理器数量。完成的 Allparrun 脚本如下所示。
#!/bin/bash
cd ${0%/*} || exit 1
source $WM_PROJECT_DIR/bin/tools/RunFunctions
function nProcs
{
n=`grep "numberOfSubdomains" system/decomposeParDict \
| sed "s/numberOfSubdomains\s//g" \
| sed "s/;//g"`
echo $n
}
PWD=`pwd`
for d in `find $FOAM_RUN/simulations -type d -maxdepth 1`
do
# Jump into the current case directory
cd $d
n=`nProcs`
application=`getApplication`
runApplication decomposePar
# Depending on the environment of your HPC, this must be
# adjusted accordingly. Remember to provide a proper
# machine file, otherwise all jobs will be started on the
# master node, which is undesirable in any way.
mpirun -np $n $application -parallel > log &
# Jump back
cd $PWD
done
对于最简单的情况,作业排队和提交系统不可用,您只需向 mpirun 提供一个machine文件。machine文件包含 HPC 集群网络上计算节点的 IP 地址或主机名。有关此主题的更多信息,请参阅您的 HPC 集群管理团队提供的相应用户手册。
提示:请记住,在这种情况下,对 mpirun 的调用会将所有作业作为机器上的本地作业启动。为了在 HPC 集群上启动它并使用其计算节点,其他步骤是必要的,具体取决于特定的集群配置,因此此处省略。
8.2.2 参数变化
参数变化包括对具有不同物理和离散化参数的许多模拟的预处理,这需要自动化。为了在 OpenFOAM 中模拟参数研究,可以使用 shell 脚本、Python 脚本或可用的 OpenFOAM 实用程序来克隆模拟并在基于文本的输入(配置)文件中调整它们的参数。由于 OpenFOAM 是为命令行使用而构建的,因此 OpenFOAM 比其他基于 GUI 的 CFD 平台更适合自动化。
此示例涵盖二维 NACA0012 翼型的参数化。网格生成是使用 blockMesh 应用程序完成的,网格使用 mirrorMesh 应用程序进行镜像。参数研究调查了攻角α对升力和流动空气对翼型施加的阻力的影响。参数研究由 15 次模拟组成,攻角从 α = 0° 到 α = 15°,导致升力 w.r.t 的粗略分布。然后通过在前 15 个收敛后自动创建新模拟,在图中的峰值处细化初始升力分布。如果没有自动化,CFD 项目中的大量参数变化会很快成为一项费力且容易出错的活动。
使用 shell 脚本进行自动化是可能的,但很麻烦,因为有效地操作 OpenFOAM 配置文件需要大量的源代码,以及 shell 脚本如何处理字母数字计算。
Python 脚本语言可以直接替代 shell 脚本,进一步简化了模拟结果的处理和可视化。此外,许多基于 Python 的库已经具有旨在支持数值模拟过程的功能,例如插值方法、求根方法、数据处理和分析库、机器学习等。一个 Python 项目已经实现了 OpenFOAM 模拟的参数变化自动化所需的许多功能:PyFoam。
PyFoam 项目由可以操作 OpenFOAM 数据的不同 Python 模块组成。除了这个库部分,PyFoam 已经提供了许多不同的即用型应用程序来简化不同的任务。
命令行中的 Tab-completion 显示了许多可用 PyFoam 应用程序的列表;在这里,我们只评论其中的几个:pyFoamClearCase.py 清除 OpenFOAM 模拟案例目录中先前计算的结果,pyFoamPlotWatcher.py 从 OpenFOAM 求解器的日志文件中实时呈现残差图,pyFoamRunParameterVariation.py 创建参数研究来自参数向量数组和模板案例的笛卡尔积。
PyFoam 可执行文件建立在 PyFoam 库之上,与以下涵盖 PyFoam 预处理应用程序编程的示例相同。在 Python 脚本中使用 PyFoam 库可以对 OpenFOAM 案例进行自定义操作。此外,可以使用 subprocess.call Python 子模块以直接的方式在 Python 中执行 OpenFOAM 可执行文件。对于这个例子,我们假设有一些 Python 的基本背景知识,并且机器上可以使用 PyFoam。
提示:PyFoam 可以使用 Python 的 pip 包安装程序通过 sudo pip install PyFoam 安装,或者在没有 root 权限的情况下使用 pip install --user PyFoam 安装。
尽管可以使用 PyFoam 从 OpenFOAM 操作 CFD 结果,但必须了解其操作大型数据数组(场变量值)的运行速度比使用 C++ 等编译语言要慢一些。这个例子侧重于参数变化研究的准备,而不是处理 OpenFOAM 模拟产生的物理场。
OpenFOAM 中的参数研究由许多具有不同配置文件的模拟文件夹组成。模拟文件夹都是从相同的输入(模板)模拟文件夹生成的。在这个例子中,我们将重新使用第 4 章中的模拟:ofprimer/cases/chapter04/naca 作为参数变化的模板案例。
提示:正确设置模板模拟案例至关重要,因为所有参数化案例都是从中创建的。
在为更复杂的参数研究编写预处理应用程序之前,有必要了解使用 pyFoamRunParameterVariation.py 已经可以实现的目标。 PyFoam 应用程序具有大量文档,可以使用命令行中的 --help 选项显示这些文档。执行 pyFoamRunParameterVariation.py --help 会显示一个广泛的选项列表,此处并未全部涵盖。
将参数研究目录结构的生成与真实场景中的网格划分和仿真执行分开是一种很好的做法。这样,网格生成和模拟在分解问题的子域和研究参数中并行运行。换句话说,我们首先串行生成模拟文件夹结构,因为这仅涉及文本文件的操作。然后使用 HPC 资源上的工作负载管理器对每个参数向量并行运行网格化,然后进行各自的模拟。为了实现这种设置,pyFoamRunParameterVariation.py 需要一组特定的选项,这些选项包含在名为 create_naca_study.py 的 Python 脚本中,以便在有效的工作流程中重复使用。
提示:脚本 create_naca_study.py 可以在 naca 模板模拟案例旁边的 ofprimer/cases/chapter04 文件夹中找到。
在 create_naca_study.py 中传递给 pyFoamRunParameterVariation.py 的选项如下所示:
- --every-variant-one-case-execution 确保为变量中的每个参数向量生成一个 OpenFOAM 模拟案例,
- --create-database 存储模拟 ID 和参数向量之间的关系(对于再现结果至关重要)
- --no-mesh-create 防止网格生成
- --no-execute-solver 阻止求解器(模拟)执行
- --cloned-case-prefix 用于将此参数研究与其他研究区分开来
在 create_naca_study.py 脚本(如下所示)中存储对 pyFoamRunParameterVariation.py 的此类调用的“配置”很有用:这简化了模拟工作流程并确保轻松再现结果。
#!/usr/bin/env python
import argparse
import sys
from subprocess import call
parser = argparse.ArgumentParser(description='Runs \
pyFoamRunParameterVariation.py to create simulation folders \
without generating the mesh.')
parser.add_argument('--study_name', dest="study_name", \
type=str, required=True, \
help='Name of the parameter study.')
parser.add_argument('--parameter_file', dest="parameter_file", \
type=str, required=True,
help='PyFoam .parameter file')
parser.add_argument('--template_case', dest="template_case", \
type=str, required=True,
help='Parameter study template case.')
args = parser.parse_args()
if __name__ == '__main__':
args = parser.parse_args(sys.argv[1:])
prefix = args.study_name + "_" + args.parameter_file
call_args = ["pyFoamRunParameterVariation.py",
"--every-variant-one-case-execution",
"--create-database",
"--no-mesh-create",
"--no-server-process",
"--no-execute-solver",
"--no-case-setup",
"--cloned-case-prefix=%s" % prefix,
args.template_case,
args.parameter_file]
call(call_args)
下列程序片段显示了 naca 案例的参数,其中只有运动粘度发生变化。其列出并存储在 naca.parameter 文件中的值应该在 naca 案例的 constant/transportProperties 文件中以某种方式替换。
values
{
solver ( simpleFoam );
NU
(
1e-06 2e-06 3e-06 4e-06
);
}
为确保 PyFoam 替换 constant/transportProperties 中的 值,将该文件复制到 constant/transportProperties.parameter 中,并修改 nu,如下所示。
...
transportModel Newtonian;
rho rho [ 1 -3 0 0 0 0 0 ] 1000;
nu nu [0 2 -1 0 0 0 0] @!NU!@;
...
运行以下命令:
?> ./create_naca_study.py --study_name my_study --template_case naca --parameter_file naca.parameter
从naca模拟案例模板生成清单13中列出的四个具有四个粘度值的OpenFOAM新模拟案例:
?> ls -d my_study*
my_study_naca.parameter_00000_naca
my_study_naca.parameter_00001_naca
my_study_naca.parameter_00002_naca
my_study_naca.parameter_00003_naca
如果清单13中定义了多个参数向量,则PyFoam将构造这些向量及其各自的模拟文件夹的笛卡尔积。大的参数变化要求唯一的模拟id (00000、00001、……) 和参数向量之间的关系。这很容易用下面的命令实现:
?> pyFoamRunParameterVariation.py --list-variations naca naca.parameter
==============================
4 variations with 1 parameters
==============================
==================
Listing variations
==================
Variation 0 : {'NU': 1e-06}
Variation 1 : {'NU': 2e-06}
Variation 2 : {'NU': 3e-06}
Variation 3 : {'NU': 4e-06}
用PyFoam的pyFoamRunParameterVariation.py涵盖了现有的OpenFOAM仿真参数的变化,接下来的步骤涉及网格的生成和仿真。
下一个示例涵盖使用PyFoam库中的子模块对参数变化脚本进行编程。当参数变化的生成超出参数向量的笛卡尔乘积,或者更复杂的计算确定参数值时,此任务变得相关。
在详细介绍编写自定义的PyFoam脚本之前,将提供有关仿真的必要背景信息。使用块网格生成对称网格,该块网格由图8.1中概述的三个块组成。调整块的分级,以使从块1到2和从2到3的网格大小没有明显变化。为了解决沿翼型的粘性边界层,在NACA轮廓附近生成了相当小的单元。
根据图8.1中所示的标记来命名所有patch。顶点数由两个用破折号分隔的数字表示。机翼上未沿图形法线方向定向的所有边均使用blockMesh的polyLine生成,其中根据定义任何两位数NACA轮廓的函数计算站。蓝色入口的顶点也是如此-但不是使用两位数的NACA多项式,而是使用四分之一圆。这使网格看起来更具视觉吸引力,并消除了入口和侧面之间的任何边界条件问题。
计算域的所有维度以及NACA分布本身都可以从图8.1中获得。 所采用的求解器是simpleFoam,并将以串行方式执行。
注:cases/chapter 04/naca案例仅用于网格生成和参数变化,而不是用于获得物理结果。
Python脚本的编程从导入必要的模块开始,如清单14所示。
# 导入PyFoam包
from PyFoam.RunDictionary.SolutionDirectory import SolutionDirectory
from PyFoam.RunDictionary.ParsedParameterFile import ParsedParameterFile
from PyFoam.Basics.DataStructures import Vector
from numpy import linspace,sin,cos,array
from os import path, getcwd
对于本节中介绍的示例,有三个PyFoam子模块非常重要:
- SolutionDirectory:处理整个案例并提供对其数据的轻松访问以及将案例克隆到不同目录的方法
- ParsedParameterFile:读取任何OpenFoam字典并提供对它的访问,就像它是Python字典一样
- Vector:处理向量的操作
用于解析命令行参数和文件路径以及在自定义参数变体中执行计算的模块(参见清单15)直接跟随清单14中的PyFoam模块。
# 程序清单15
# 导入PyFoam模块
# Commandline arguments and paths
import os
import sys
import argparse
# Parameter variation
import numpy as np
from numpy import linspace,sin,cos,array,pi
import yaml
自定义参数研究将改变NACA0012翼型的迎角,在本例中,这需要向量绕-y坐标轴旋转,由清单16中的函数实现。
# 程序清单16
def rot_matrix(angle_deg):
angle_rad = angle_deg * pi / 180.
return np.array([[cos(angle_rad),0,-sin(angle_rad)],[0,1,0]
[sin(angle_rad), 0, cos(angle_rad)]])
def rot_vector(vec, angle_deg):
return np.dot(rot_matrix(angle_deg), vec)
参数变化脚本通过命令行选项控制学习。 或者,可以像pyFoamRunParameterVariation.py一样控制参数变化:使用配置文件,采用CSV、JSON或YAML等标准化格式。 命令行参数由清单17所示的代码解析。 参数变化脚本的主要功能如清单18所示,并用注释对其进行了详细概述。 其核心思想是读取一个模板仿真案例,然后将该案例克隆为多个仿真案例,这些案例由与参数变化相对应的唯一标识符标识。
参数变化脚本通过命令行选项控制研究。或者可以pyFoamRunParameterVariation.py使用配置文件(采用CSV、JSON或YAML等标准化格式)来控制参数变化。命令行参数由清单17所示的代码解析。参数变化脚本的主要功能如清单18所示,并通过注释详细概述了它。核心思想是读取模板仿真案例,然后将该案例克隆成多个仿真案例,由对应于参数变化的唯一标识符(ID)来标识。
# 程序清单17
parser = argparse.ArgumentParser(description='Generates simulation cases for parameter study using PyFoam.')
parser.add_argument('--template_case',dest="template_case", type=str,help='OpenFOAM template case.', required=True)
parser.add_argument('--study_name', dest="study_name", type=str,help='Name of the parameter study.', required=True)
parser.add_argument('--alpha_min', dest="alpha_min", type=float,help='Minimal angle of attack in degrees.',required=True)
parser.add_argument('--alpha_max', dest="alpha_max", type=float,help='Maximal angle of attack in degrees.',required=True)
parser.add_argument('--n_alphas', dest="n_alphas", type=int,help='Number of angles between alpha_min and alpha_max.',required=True)
args = parser.parse_args()
# 程序清单18
if __name__ == '__main__':
args = parser.parse_args(sys.argv[1:])
# Distribute angles of attack
angles = np.linspace(args.alpha_min, args.alpha_max, args.n_alphas)
# Initialize the template case
template_case = SolutionDirectory(args.template_case)
# Initialize the parameter dictionary
param_dict = {}
# For every variation
for variation_id,alpha in enumerate(angles):
# Add variation-d : parameter vector to parameter dictionary.
param_dict[variation_id] = {"ALPHA" : float(alpha)}
# Clone the template case into a variation ID case.
name = "%s-%08d" % (args.study_name, variation_id)
case_name = os.path.join(os.path.curdir, name)
cloned_case = template_case.cloneCase(case_name)
# Read the velocity field file.
u_file_path = os.path.join(cloned_case.name,"0", "U")
u_file = ParsedParameterFile(u_file_path)
# Read the velocity inlet boundary condition and internal field.
u_inlet = u_file["boundaryField"]["INLET"]["value"]
u_internal = u_file["internalField"]
# Rotate the velocity clockwise by alpha around (-y).
u_numpy = np.array(u_inlet[1])
u_numpy = rot_vector(u_numpy, alpha)
# Set inlet and internal velocity.
u_inlet.setUniform(Vector(u_numpy[0],u_numpy[1],u_numpy[2]))
u_internal.setUniform(Vector(u_numpy[0],u_numpy[1],u_numpy[2]))
u_file.writeFile()
# Store variation ID : study parameters into a YAML file.
with open(args.study_name + '.yml', 'w') as param_file:
yaml.dump(param_dict, param_file, default_flow_style=False)
此示例中的每个参数变量都由单个标量值组成:迎角α。通常,通过参数空间中的n维参数向量来识别参数变化,其中n对应于仿真中变化的参数的数目。在这种情况下,改变迎角需要速度场围绕−y坐标轴方向旋转。
使用PyFoam读取速度文件,并从中获得入口边界条件和内部速度场。然后设置入口边界条件和初始内部值,以达到特定的迎角。一旦像这样初始化速度场,就会写入其文件。然后将唯一参数变量的ID与参数向量相关联的字典保存为YAML文件。这个ID -参数向量映射也由pyFoamRunParameterVariation.py以PyFoam特定的格式保存。这里,YAML被用作一种标准格式,在Python中很容易操作。尽管在这个小的示例脚本中只有一个参数发生了变化,但该示例显示了如何将PyFoam的主要子模块与标准Python模块一起使用,以扩展OpenFOAM中的参数变化,从而完全控制该变化。例如,下一步是通过应用条件来禁用没有意义的参数向量,从而减少参数向量的全笛卡尔积。
该脚本位于代码库中,如cases/chapter 04/parametricStudy.py。称之为在0 °和10 °之间以10个步长改变迎角,即
?> ./parametricStudy.py --study_name angle-of-attack \
--template_case naca --alpha_min 0 \
--alpha_max 10 --n_alpha 10
得到结果为:
?> ls
angle-of-attack-00000001
angle-of-attack-00000002
angle-of-attack-00000003
...
angle-of-attack.yml
angle-of-attack.yml文件中包含ID参数向量映射:
0:
ALPHA: 0.0
1:
ALPHA: 1.1111111111111112
2:
ALPHA: 2.2222222222222223
...
虽然naca情况的模拟参数不能保证本例中物理结果的正确性,但参数研究的两个极端变量的流线如图8. 2所示。

仿真结果的后处理OpenFOAM基于function objects。第12章介绍了OpenFoam中function object的使用、设计和实现,本节只介绍它们在后处理中的应用。顾名思义,后处理一般是在仿真完成后对仿真数据进行处理。 function object用对仿真运行时生成的仿真结果的主动处理取代了对完成的仿真数据的后处理。 主动处理仿真结果是非常有益的,因为它提供了仿真的主动概述,使得在出现错误的情况下尽早停止仿真成为可能,这反过来又节省了计算资源和开发时间。 OpenFoam中的function object可以由用户在运行时(当模拟开始时)根据controlDict字典文件中的配置进行选择,因此不需要维护大量不同的后处理应用程序。 可以使用一个后处理应用程序postProcess,它重用(选择、配置和运行)function object来对生成的仿真数据进行后处理。 用于主动处理的function object的一个例子:
$FOAM_TUTORIALS/compressible/sonicFoam/RAS/nacaAirfoil
在本例的controlDict文件中,翼型的力系数由清单19所示的function object项定义。 当模拟开始时,forceCoeffs将处理计算Wall_4边界上的力系数所需的物理场。 结果数据写入postProcessing/forces/0/coefficient.dat文件中,并且可以在模拟运行时进行分析,最好使用Jupyter笔记本。 使用Jupyter笔记本查看和分析OpenFOAM仿真中由OpenFOAM function object生成的活动处理结果带来了两个重要的好处。Jupyter笔记本可以在模拟运行时在Web浏览器中刷新,从而可以在运行时更新数据分析和检查模拟。此外,Jupyter笔记本电脑可以在远程机器(HPC集群)上安全启动,并在PC/笔记本电脑上的Web浏览器中查看。支持此功能的function object可在模拟完成后通过运行模拟案例文件夹中的postProcess应用程序来执行。有关不同后处理function object及其用法的信息可在扩展代码指南中获得,因此本节仅提供此简要概述。
functions
{
forces
{
type forceCoeffs;
libs (forces);
writeControl writeTime;
patches
(
wall_4
);
rhoInf 1;
CofR (0 0 0);
liftDir (-0.239733 0.970839 0);
dragDir (0.970839 0.239733 0);
pitchAxis (0 0 1);
magUInf 618.022;
lRef 1;
Aref 1;
}
}
当OpenFOAM中不存在执行所需计算的类似应用程序或函数对象时,可编程定制后处理应用程序。
本节介绍了一个计算上升气泡面积和速度的示例后处理应用程序的编程。 在这个例子中,上升的气泡是用一个用于跟踪气泡的场的水平集来近似的。 用interIsoFoam求解器对上升气泡进行了模拟[4,5]。interIsoFoam求解器实现了非结构分段线性界面计算(PLIC)流体体积方法[3]的一种变体(参考[2]最近的评论)。
在interIsoFoam求解器中,由符号距离重建等值面()[5]和体积分数之间存在一个选择。 由于重构气泡中的差异可以忽略不计,因此在本例中,我们使用作为水平集场。 因此,气泡是一个水平集: 体积分数与网格中心相关联,在点处近似为以重建等值面。 OpenFOAM中的等值面重建算法实现了正则化推进四面体算法[6],该算法在与相交的网格边对使用线性逼近。 利用反向距离加权(IDW)插值方法,从以网格为中心的体积分数求取网格角点体积分数值。
等值面算法的任务是将气泡表面重建为三角形网格,从场场等值面体积分数场(本例)。 在这个例子中,气泡的面积是三角形等值面网格的面积,并且气泡质心同样是网格等值面的中心根据气泡质心的时间演化计算气泡速度。
本章依赖于来自OFPrimer存储库的Cases/Chapter04/RisingBubble2D案例。
示例应用程序名为isoSurfaceBubbleCalculator,它也可以在源代码库中找到,位于文件夹:
applications/utilities/postProcessing/
isoSurfaceBubbleCalculator使用的库的名称为bubbleCalc,其源代码位于文件夹:
src/bubbleCalc
该示例从实现bubbleCalc库开始,然后是isoSurfaceBubbleCalculator后处理应用程序。
// 程序清单20
isoSurfacePoint
(
const volScalarField& cellValues,
const scalarField& pointValues,
const scalar iso,
const isoSurfaceParams& params = isoSurfaceParams(),
const bitSet& ignoreCells = bitSet()
);
使用等值面对上升的气泡建模是向现有类添加功能的原型示例。对于等值面,此类称为isoSurfacePoint,其源文件位于文件夹:
$FOAM_SRC/sampling/surface/isoSurface
当然,需要扩展的类通常是未知的,但可以通过在扩展代码指南中搜索具有类似功能的类来找到它,
isoSurfacePoint类的接口显示,类构造函数负责重构等值面三角形网格,如程序清单20所示。
isoSurfacePoint构造函数对上升气泡规定了以下要求:
- 应在单元格角点(pointValues)处计算附加物理场
- 成员函数尚不可用于面积、质心或上升速度计算。
上述项目为isoSurfacePoint类提供了附加功能。在后处理应用程序中使用全局函数和数据实现新计算是可能的,但这使得无法在其他设置中重复使用它们:函数对象或另一个应用程序。
因此,等值面计算将被封装到一个名为isoBubble的新类中,并编译到一个可动态加载的共享库BubbleCalc中。 将后处理代码编译到共享库中,可以在不同的应用程序和其他可能需要的库之间共享功能。 一个例子可以是计算两个气泡之间的符号距离。
isoSurfacePoint需要一个与单元角点关联的附加pointField来计算等值面,而气泡重建仅依赖于以单元为中心的volScalarField,因此pointField的计算被封装到一个小类中,如清单21所示。此示例中使用的是反向距离加权插值,也可以使用其他插值方法。
//程序清单21
class isoPointFieldCalc
{
// Computed point iso-field.
scalarField field_;
public:
isoPointFieldCalc(const volScalarField& isoField)
{
this-> calcPointField(isoField);
}
virtual void calcPointField(const volScalarField& isoField)
{
volPointInterpolation pointInterpolation (isoField.mesh());
field_ = pointInterpolation.interpolate(isoField)();
}
virtual ~isoPointFieldCalc() = default;
const scalarField& field() const
{
return field_;
}
};
清单22显示了isoBubble的私有类接口。
class isoBubble:public regIOobject
{
isoPointFieldCalc isoPointField_;
// Bubble geometry described with an iso-surface mesh.
isoSurfacePoint bubbleSurf_;
// Number of zeros that are prepended to the timeIndex()
// for written VTK files.
label timeIndexPad_;
// Output format.
word outputFormat_;
fileName paddWithZeros(const fileName& input) const;
从类声明开始,注意isoBubble继承自regIOobject类。OpenFOAM将对象的IO操作封装在regIOobject类中,该类注册到对象注册表。对象注册表是一个类,当在应用程序代码中执行写操作时,它调用所讨论对象的写成员函数。它也是程序中的全局对象,向订阅它的所有对象发出写入请求。这种设计代表了一种称为“观察者模式”([1])的常见面向对象设计(OOD)模式,并且由于以下原因(其中),它非常适合CFD求解器:
- 一个面向对象的CFD应用程序可能会使用许多对象
- 对象不必在每个时间步长被写出。写入频率遵循从字典文件读取并由注册表应用的用户定义的规则。
调用runtime.write()使Foam::Time注册表循环访问一系列指向已注册对象(在观察者模式中为“主题”)的指针,并在每个时间步骤结束时将write调用转发给每个已注册对象。 只有当有问题的时间步是为输出指定的时间步时,才会发生实际的写入。 例如,用户可以规定输出每N个时间步进行一次。
为了使用OpenFOAM中可用的写入控制(例如,每5个时间步长或每0.01秒)写入isoBubble对象,isoBubble类从regIOobject类公开继承。isoBubble的padWithZeros私有成员函数扩展文件名,以便paraView可视化应用程序将其作为时间序列进行读取。然后,指定VTK格式的实际输出将从isoBubble委托给isoSurface类。这些文件被写入实例目录中,其名称是作为IOobject构造函数参数的子参数给出的。
isoBubble类的私有属性为:
- isoPointFieldCalc,用于根据以网格为中心的等值面场值计算网格角点等值面场值
- isoSurfacePoint执行等值面重构并存储曲面网格数据
- 等值面格式化输出所需的数据和功能
在OpenFOAM模拟中,点场是默认不可用的,OpenFOAM在数学模型中使用网格中心物理场作为因变量。 isoSurfacePoint不存在的空构造函数和以网格为中心(vol)场作为参数的构造函数排除了从isoSurfacePoint继承的可能性。 取而代之的是使用组合,isoPointCalc对象计算isoSurfacePoint构造函数所需的点场。
通过将计算出的isoPointField和所有必要的参数传递给构造函数,isoSurfacePoint类负责等值面网格的实际重构,如清单23所示。
// 程序清单23
isoBubble::isoBubble
(
const IOobject& io,
const volScalarField& isoField,
scalar isoValue,
bool isTime ,
label timeIndexPad,
word outputFormat,
bool regularize
)
:
regIOobject(io, isTime),
isoPointField_(isoField),
bubbleSurf_(isoField, isoPointField_.field(), isoValue),
timeIndexPad_(timeIndexPad),
outputFormat_(outputFormat)
{}
isoSurfacePoint的成员函数可用于执行气泡的中心和面积计算。我们将气泡的面积计算为等值面面积法向矢量的大小之和: 气泡中心计算为所有等值面网格点的代数平均值: 其中N是等值面网格的点数。计算由isoBubble::area和isoBubble::center成员函数执行,如清单24所示。
// 程序清单24
scalar isoBubble::area() const
{
scalar area = 0;
const pointField& points = bubblePtr_-> points();
const List<labelledTri> & faces = bubblePtr_-> localFaces();
forAll (faces, I)
{
area += mag(faces[I].normal(points));
}
return area;
}
vector isoBubble::center() const
{
const pointField& points = bubblePtr_-> points();
vector bubbleCenter (0,0,0);
forAll(points, I)
{
bubbleCenter += points[I];
}
return bubbleCenter / bubblePtr_-> nPoints();
}
在重用了isoSurface类并封装了IO操作以及气泡区域和中心的计算之后,现在可以轻松地编写应用程序并实例化任意多的气泡对象。 isoBubble类是为可供选择的计算而准备的,并且可以与其他与气泡相关的计算一起扩展。
为了方便地与其他人(人或客户端程序)共享isoBubble的实现,isoBubble实现被设置为某个库(即bubbleCalc库)的一部分。列出foam_user_libbin中,以避免污染OpenFOAM系统的库安装目录。
isoBubble.C
LIB = $(FOAM_USER_LIBBIN)/libbubbleCalc
options文件列出了所有必要的目录路径,这些目录包含isoBubble中使用的头文件,以及安装库代码的目录路径。预编译库代码允许我们扩展现有代码,而不必总是重新编译所有代码。通过在bubbleCalc目录中发出命令wmake libso,使用OpenFOAM构建系统wmake编译该库。
EXE_INC = \
-I$(LIB_SRC)/finiteVolume/lnInclude \
-I$(LIB_SRC)/meshTools/lnInclude \
-I$(LIB_SRC)/triSurface/lnInclude \
-I$(LIB_SRC)/surfMesh/lnInclude \
-I$(LIB_SRC)/surfMesh/MeshedSurfaceProxy/ \
-I$(LIB_SRC)/sampling/lnInclude
EXE_LIBS = \
-lmeshTools \
-lfiniteVolume \
-ltriSurface \
-lsampling
通过编译的库,可以在示例后处理实用程序isoSurfaceBubbleCalculator中使用isoBubble类。
示例后处理实用程序isoSurfaceBubbleCalculator可在代码存储库的applications/utilities/ postProcessing文件夹中找到。
首先,必须包含isoBubble类的声明,才能使库在应用程序中使用。此外,若要处理既有模拟结果,请使用时间步长提取器。相应的代码片段如清单27所示。
// 程序清单27
#include "fvCFD.H"
#include "timeSelector.H"
#include "isoBubble.H"
using namespace bookExamples;
接下来,为应用程序分配一个命令行选项,然后初始化根用例、模拟时间和网格,如清单28所示。
// 程序清单28
int main(int argc, char *argv[])
{
argList::addOption
(
"isoField",
"Name of the field whose level set is the bubble surface."
);
#include "setRootCase.H"
#include "createTime.H"
#include "createMesh.H"
if (!args.found("isoField"))
{
FatalErrorInFunction
<< "Provide the name of the iso-surface field."
<< "Use '-help' for more information."
<< abort(FatalError);
}
负责实际计算的应用程序部分如清单29所示。
Foam::instantList timeDirs = Foam::timeSelector::select0(runTime, args);
OFstream bubbleFile("bubble.csv");
bubbleFile << "TIME,AREA,CENTER_X,CENTER_Y,CENTER_Z\n";
forAll(timeDirs, timeI)
{
runTime.setTime(timeDirs[timeI], timeI);
Info<< "Time = " << runTime.timeName() << endl;
volScalarField isoField
(
IOobject
(
args.get<word> ("isoField"),
runTime.timeName(),
mesh,
IOobject::MUST_READ,
IOobject::NO_WRITE
),
mesh
);
isoBubble bubble
(
IOobject
(
"bubble",
"bubble",
runTime,
IOobject::NO_READ,
IOobject::AUTO_WRITE
),
isoField
);
const auto area = bubble.area();
const auto center = bubble.center();
Info << "Bubble area = " << bubble.area() << endl;
Info << "Bubble center = " << bubble.center() << endl;
bubbleFile << runTime.timeOutputValue() << ","
<< area << ","
<< center[0] << "," << center[1] << "," << center[2] << "\n";
bubble.write();
}
从regIOobject继承会强制客户端代码使用IOobject初始化isoBubble对象。IOobject构造函数的参数定义如下:
“bubble”。对象的名称(在本例中,是用于保存等值面数据的文件名)“bubble”。实例,或存储对象的目录(在本例中与文件名相同)runTime。对象注册到的对象注册表-我们希望isoBubble的IO操作由模拟时间来调节,IOobject::。为IOobject定义运行时wirte/read操作的标记(枚举)inputField。跟踪的iso-field。
然后使用timeSelector类在模拟案例目录的文件和文件夹中查找时间步长(迭代)目录。在每次迭代中,读取等值线场,重建等值线气泡对象,计算气泡的面积和中心,并将气泡等值线曲面网格写入磁盘。从这个意义上说,isoBubble类的行为方式与任何其他OpenFOAM类的行为方式相同。
通过调用Allrun脚本来运行模拟,初始化气泡,运行interIsoFoam解算器并调用以计算气泡等参曲面。
> isoSurfaceBubbleCalculator -isoField alpha.air
气泡曲面作为一系列“vtk”文件存储在气泡目录中。物理时间、气泡面积和气泡中心坐标存储在bubble.csv中。
图8.3中等值面的可视化显示了OpenFOAM中的2D等值面算法与ParaView中的2D等值面算法之间的一些差异(在isoSurface.H文件中提到)。

在Jupyter笔记本iso-bubble.ipynb中,使用Pandas Python数据分析库处理buble.csv格式的isoSurfaceBubbleCalculator的CSV输出。清单30列出了Python pandas代码。这个使用pandas的小例子只是为了向读者介绍pandas库:pandas可以进行比这个例子中演示的更强大的数据处理。不过,有两个优点可以提高对数据处理代码的理解:阅读CSV文件很简单,列通过它们的名称访问,导数的计算非常简单。除了这些简单的优点外,panda在CFD环境中最大的好处是它能够轻松地存储和处理使用panda.MultiIndex with pandas. DataFrame进行参数研究的结果。
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams["figure.dpi"] = 200
rcParams["text.usetex"] = True
bubble_csv = pd.read_csv("bubble.csv")
plt.plot(bubble_csv["TIME"], bubble_csv["AREA"])
plt.xlabel("Time in $s$")
plt.ylabel("Area in $m^2$")
plt.savefig("iso-bubble-area.png")
plt.plot(bubble_csv["TIME"], bubble_csv["CENTER_Y"])
plt.ylabel("Y-coordinate of the bubble center")
plt.xlabel("Time in $s$")
plt.savefig("iso-bubble-center-y.png")
y_velocity = bubble_csv["CENTER_Y"].diff() / bubble_csv["TIME"].diff()
plt.plot(bubble_csv["TIME"], y_velocity)
plt.ylabel("Bubble y-velocity in $m/s$")
plt.xlabel("Time in $s$")
plt.savefig("iso-bubble-center-y-velocity.png")
气泡面积随时间的分布如图8.4所示。当气泡上升到溶液域的顶壁并在其上扩展时,面积几乎减半。图8.5给出了用式(8.3)计算的气泡质心的Y坐标分布。该分布在肉眼看来足够平滑。然而,用有限差分法从式(8.3)中气泡质心的Y坐标计算气泡上升速度的Y−分量容易出错。图8.6证实了这种精确度的灾难性损失。以下建议的练习改进了示例后处理计算中气泡上升速度的评估。
练习:
- 如果用更精确的时间有限差分格式计算上升速度,会发生什么?扩展isoBubble以计算气泡速度,作为在气泡等值面的三角形中心处计算的平均速度?提示:使用interpolationCellPoint在三角形中心插入速度。
- 编写另一个后处理应用程序,仅使用alpha.air和U场计算气泡速度。计算速度的差异是什么?这些差异来自哪里?
- Erich Gamma et al. Design patterns: elements of reusable object-oriented software. Addison-Wesley Longman Publishing Co., Inc., isbn: 0-201-63361-2.
- Tomislav Marić, Douglas B Kothe, and Dieter Bothe. “Unstructured un-split geometrical Volume-of-Fluid methods–A review”. In: Journal of Computational Physics 420 (2020), p. 109695.
- William J Rider and Douglas B Kothe. “Reconstructing volume tracking”. In: Journal of computational physics 141.2 (1998), pp. 112–152.
- Johan Roenby, Henrik Bredmose, and Hrvoje Jasak. “A Computational Method for Sharp Interface Advection”. In: R. Soc. OpenSci. 3.11 (2016). Doi: 10.1098/rsos. 160405. Url: http://arxiv.org/abs/1601.05392.
- Henning Scheufler and Johan Roenby. “Accurate and efficient surface reconstruction from volume fraction data on general meshes”. In: J. Comput. Phys. 383 (Apr. 2019), pp. 1–23. Issn: 10902716. Doi: 10.1016/j.jcp. 2019.01.009. ArXiv: 1801.05382.
- Graham M Treece, Richard W Prager, and Andrew H Gee. “Regularised marching tetrahedra: improved iso-surface extraction”. In: Computers & Graphics 23.4 (1999), pp. 583–598.
求解器应用程序(求解器)在结构上与任何其他 OpenFOAM 应用程序没有区别:它使用在不同 OpenFOAM 库中实现的算法。求解器不是对物理场进行算术处理或以某种方式操纵网格,而是近似于对物理过程建模的偏微分方程 (PDE) 求解解。第 1 章简要概述了 OpenFOAM 中用于 PDE 离散化的 FVM。OpenFOAM 求解器根据求解器模拟的物理过程分为不同的类别。它们可以通过使用预定义的别名命令位于 OpenFOAM 安装中:
sol
切换到 OpenFOAM 中所有可用求解器的父目录,或者手动更改为 FOAM_SOLVERS
作为示例求解器,我们为两相流的 DNS 选择了 interFoam 求解器。 interFoam 求解器实现了一个数学模型,该模型将两种分离的不混溶流体(相)的流动描述为单一流体(连续体)的流动。通过使用额外的标量场 - 体积分数场 (α) 来完成相分离。该方法称为VOF方法,α表示主相的填充水平,并采用区间[0,1]中的值。有关VoF方法的更多信息,请参见[8]。
interFoam 的源代码文件位于 $FOAM_SOLVERS/multiphase/interFoam。列出 interFoam 目录的内容,结果如下:
```bash
ls <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.02778em;">FO</span><span class="mord mathnormal">A</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3283em;"><span style="top:-2.55em;margin-left:-0.109em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right:0.05764em;">S</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord mathnormal" style="margin-right:0.02778em;">O</span><span class="mord mathnormal">L</span><span class="mord mathnormal" style="margin-right:0.22222em;">V</span><span class="mord mathnormal" style="margin-right:0.05764em;">ERS</span><span class="mord">/</span><span class="mord mathnormal">m</span><span class="mord mathnormal">u</span><span class="mord mathnormal">lt</span><span class="mord mathnormal">i</span><span class="mord mathnormal">p</span><span class="mord mathnormal">ha</span><span class="mord mathnormal">se</span><span class="mord">/</span><span class="mord mathnormal">in</span><span class="mord mathnormal">t</span><span class="mord mathnormal" style="margin-right:0.02778em;">er</span><span class="mord mathnormal" style="margin-right:0.13889em;">F</span><span class="mord mathnormal">o</span><span class="mord mathnormal">ama</span><span class="mord mathnormal">lp</span><span class="mord mathnormal">ha</span><span class="mord mathnormal" style="margin-right:0.05764em;">S</span><span class="mord mathnormal">u</span><span class="mord mathnormal">Sp</span><span class="mord">.</span><span class="mord mathnormal">Hcorrec</span><span class="mord mathnormal" style="margin-right:0.13889em;">tP</span><span class="mord mathnormal">hi</span><span class="mord">.</span><span class="mord mathnormal">Hcre</span><span class="mord mathnormal">a</span><span class="mord mathnormal">t</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.13889em;">F</span><span class="mord mathnormal">i</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">d</span><span class="mord mathnormal">s</span><span class="mord">.</span><span class="mord mathnormal" style="margin-right:0.08125em;">H</span><span class="mord mathnormal">ini</span><span class="mord mathnormal" style="margin-right:0.07153em;">tC</span><span class="mord mathnormal">orrec</span><span class="mord mathnormal" style="margin-right:0.13889em;">tP</span><span class="mord mathnormal">hi</span><span class="mord">.</span><span class="mord mathnormal" style="margin-right:0.08125em;">H</span><span class="mord mathnormal">in</span><span class="mord mathnormal">t</span><span class="mord mathnormal" style="margin-right:0.02778em;">er</span><span class="mord mathnormal" style="margin-right:0.13889em;">F</span><span class="mord mathnormal">o</span><span class="mord mathnormal">am</span><span class="mord">.</span><span class="mord mathnormal" style="margin-right:0.07153em;">C</span><span class="mord mathnormal">in</span><span class="mord mathnormal">t</span><span class="mord mathnormal" style="margin-right:0.02778em;">er</span><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="mord mathnormal">i</span><span class="mord mathnormal">x</span><span class="mord mathnormal">in</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal" style="margin-right:0.13889em;">F</span><span class="mord mathnormal">o</span><span class="mord mathnormal">am</span><span class="mord">/</span><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="mord mathnormal" style="margin-right:0.03148em;">ak</span><span class="mord mathnormal">e</span><span class="mord">/</span><span class="mord mathnormal">o</span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mord mathnormal" style="margin-right:0.02778em;">er</span><span class="mord mathnormal" style="margin-right:0.07847em;">I</span><span class="mord mathnormal">n</span><span class="mord mathnormal">t</span><span class="mord mathnormal" style="margin-right:0.03588em;">erDy</span><span class="mord mathnormal" style="margin-right:0.13889em;">MF</span><span class="mord mathnormal">o</span><span class="mord mathnormal">am</span><span class="mord">/</span><span class="mord mathnormal" style="margin-right:0.03588em;">pEq</span><span class="mord mathnormal">n</span><span class="mord">.</span><span class="mord mathnormal" style="margin-right:0.02778em;">Hr</span><span class="mord mathnormal">h</span><span class="mord mathnormal">o</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal">s</span><span class="mord">.</span><span class="mord mathnormal" style="margin-right:0.08125em;">H</span><span class="mord mathnormal" style="margin-right:0.10903em;">U</span><span class="mord mathnormal" style="margin-right:0.03588em;">Eq</span><span class="mord mathnormal">n</span><span class="mord">.</span><span class="mord mathnormal" style="margin-right:0.08125em;">H</span><span class="mord">‘‘‘</span><span class="mord cjk_fallback">每个求解器目录都包含许多不同的文件,这些文件伴随着主求解器实现文件,在本例中为</span><span class="mord mathnormal">in</span><span class="mord mathnormal">t</span><span class="mord mathnormal" style="margin-right:0.02778em;">er</span><span class="mord mathnormal" style="margin-right:0.13889em;">F</span><span class="mord mathnormal">o</span><span class="mord mathnormal">am</span><span class="mord">.</span><span class="mord mathnormal" style="margin-right:0.07153em;">C</span><span class="mord cjk_fallback">。当求解器实现一个由不同项耦合在一起的</span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mord mathnormal" style="margin-right:0.02778em;">D</span><span class="mord mathnormal" style="margin-right:0.05764em;">E</span><span class="mord cjk_fallback">系统时,有必要获得一个不仅满足单个</span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mord mathnormal" style="margin-right:0.02778em;">D</span><span class="mord mathnormal" style="margin-right:0.05764em;">E</span><span class="mord cjk_fallback">,而且满足所有</span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mord mathnormal" style="margin-right:0.02778em;">D</span><span class="mord mathnormal" style="margin-right:0.05764em;">E</span><span class="mord cjk_fallback">的解决方案。附加文件实现了所谓的求解算法的一部分:确定如何在</span><span class="mord mathnormal">Op</span><span class="mord mathnormal">e</span><span class="mord mathnormal">n</span><span class="mord mathnormal" style="margin-right:0.02778em;">FO</span><span class="mord mathnormal">A</span><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="mord cjk_fallback">中求解耦合偏微分方程的算法。在单独的文件中实现方程并将它们包含在主求解器应用程序中显着增加了求解器应用程序实现的求解算法的可读性。除了更好地了解求解器应用程序之外,将算法分成不同的文件使它们可以轻松地为其他求解器重用,同时避免复制源代码。包含对</span><span class="mord mathnormal" style="margin-right:0.22222em;">V</span><span class="mord mathnormal" style="margin-right:0.13889em;">OF</span><span class="mord cjk_fallback">求解器系列重要的实现的支持文件可以通过下面的命令找到:</span><span class="mord">‘‘‘</span><span class="mord mathnormal">ba</span><span class="mord mathnormal">s</span><span class="mord mathnormal">h</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">s</span></span></span></span>FOAM_SOLVERS/multiphase/VoF/
aCourantNo.H alphaEqn.H alphaEqnSubCycle.H
teAlphaFluxes.H setDeltaT.H setRDeltaT.H
共享文件可以很容易地被放置在求解器目录中的同名文件替换:wmake 构建系统首先在求解器目录中搜索要包含的文件。包含“Eqn”后缀的文件包含定义求解器正在实施的数学模型方程的源代码。这个实现是在非常高的抽象层次上完成的,使其更具人类可读性。显然,interFoam 使用了动量方程(UEqn.H)、压力方程(pEqn.H)、体积分数方程(alphaEqn.H)以及求解算法的其他支持部分。 alphaEqn.H 由不同版本的 interFoam 共享,因此存储在 $FOAM_SOLVERS/multiphase/VoF 中。
提示:每当遇到带有 Eqn 后缀的源文件时,意味着该文件包含数学模型方程的实现。
对全局字段变量进行操作且未以函数或类的形式实现的源代码分布在求解器应用程序包含的文件中。在求解器代码中包含文件 CourantNo.H,包括求解器应用程序中当前 Courant 数的计算,该计算基于全局范围内可用的场变量。为了防止代码重复,在构建系统的帮助下,共享公共源代码片段的此类文件的数量减少到最低限度。所有共享的包含文件都存储在特定文件夹中,例如:
ls <span class="katex"><span class="katex-html" aria-hidden="true"><span class="base"><span class="strut" style="height:1em;vertical-align:-0.25em;"></span><span class="mord mathnormal" style="margin-right:0.02778em;">FO</span><span class="mord mathnormal">A</span><span class="mord"><span class="mord mathnormal" style="margin-right:0.10903em;">M</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height:0.3283em;"><span style="top:-2.55em;margin-left:-0.109em;margin-right:0.05em;"><span class="pstrut" style="height:2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathnormal mtight" style="margin-right:0.05764em;">S</span></span></span></span><span class="vlist-s"></span></span><span class="vlist-r"><span class="vlist" style="height:0.15em;"><span></span></span></span></span></span></span><span class="mord mathnormal" style="margin-right:0.07153em;">RC</span><span class="mord">/</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal">ini</span><span class="mord mathnormal">t</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.22222em;">V</span><span class="mord mathnormal">o</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">u</span><span class="mord mathnormal">m</span><span class="mord mathnormal">e</span><span class="mord">/</span><span class="mord mathnormal">c</span><span class="mord mathnormal">fd</span><span class="mord mathnormal" style="margin-right:0.13889em;">T</span><span class="mord mathnormal">oo</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">s</span><span class="mord">/</span><span class="mord mathnormal" style="margin-right:0.03588em;">g</span><span class="mord mathnormal">e</span><span class="mord mathnormal">n</span><span class="mord mathnormal" style="margin-right:0.02778em;">er</span><span class="mord mathnormal">a</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord">/</span><span class="mord mathnormal">in</span><span class="mord mathnormal">c</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">u</span><span class="mord mathnormal">d</span><span class="mord mathnormal">ec</span><span class="mord mathnormal">h</span><span class="mord mathnormal">ec</span><span class="mord mathnormal" style="margin-right:0.03148em;">k</span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mord mathnormal">a</span><span class="mord mathnormal">t</span><span class="mord mathnormal">c</span><span class="mord mathnormal">h</span><span class="mord mathnormal" style="margin-right:0.13889em;">F</span><span class="mord mathnormal">i</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">d</span><span class="mord mathnormal" style="margin-right:0.13889em;">T</span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span><span class="mord mathnormal">p</span><span class="mord mathnormal">es</span><span class="mord">.</span><span class="mord mathnormal" style="margin-right:0.08125em;">H</span><span class="mord mathnormal" style="margin-right:0.10764em;">f</span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mord mathnormal" style="margin-right:0.13889em;">CF</span><span class="mord mathnormal" style="margin-right:0.02778em;">D</span><span class="mord">.</span><span class="mord mathnormal" style="margin-right:0.08125em;">H</span><span class="mord mathnormal">ini</span><span class="mord mathnormal" style="margin-right:0.07153em;">tC</span><span class="mord mathnormal">o</span><span class="mord mathnormal">n</span><span class="mord mathnormal">t</span><span class="mord mathnormal">in</span><span class="mord mathnormal">u</span><span class="mord mathnormal">i</span><span class="mord mathnormal">t</span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span><span class="mord mathnormal" style="margin-right:0.05764em;">E</span><span class="mord mathnormal">rrs</span><span class="mord">.</span><span class="mord mathnormal">Hre</span><span class="mord mathnormal">a</span><span class="mord mathnormal">d</span><span class="mord mathnormal">G</span><span class="mord mathnormal" style="margin-right:0.02778em;">r</span><span class="mord mathnormal">a</span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mord mathnormal">i</span><span class="mord mathnormal">t</span><span class="mord mathnormal">a</span><span class="mord mathnormal">t</span><span class="mord mathnormal">i</span><span class="mord mathnormal">o</span><span class="mord mathnormal">na</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">A</span><span class="mord mathnormal">cce</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal" style="margin-right:0.02778em;">er</span><span class="mord mathnormal">a</span><span class="mord mathnormal">t</span><span class="mord mathnormal">i</span><span class="mord mathnormal">o</span><span class="mord mathnormal">n</span><span class="mord">.</span><span class="mord mathnormal">Hre</span><span class="mord mathnormal">a</span><span class="mord mathnormal">d</span><span class="mord mathnormal" style="margin-right:0.13889em;">P</span><span class="mord mathnormal" style="margin-right:0.07847em;">I</span><span class="mord mathnormal" style="margin-right:0.07153em;">SOC</span><span class="mord mathnormal">o</span><span class="mord mathnormal">n</span><span class="mord mathnormal">t</span><span class="mord mathnormal">ro</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">s</span><span class="mord">.</span><span class="mord mathnormal">Hre</span><span class="mord mathnormal">a</span><span class="mord mathnormal">d</span><span class="mord mathnormal" style="margin-right:0.13889em;">T</span><span class="mord mathnormal">im</span><span class="mord mathnormal">e</span><span class="mord mathnormal" style="margin-right:0.07153em;">C</span><span class="mord mathnormal">o</span><span class="mord mathnormal">n</span><span class="mord mathnormal">t</span><span class="mord mathnormal">ro</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">s</span><span class="mord">.</span><span class="mord mathnormal">Hse</span><span class="mord mathnormal">t</span><span class="mord mathnormal">De</span><span class="mord mathnormal">lt</span><span class="mord mathnormal">a</span><span class="mord mathnormal" style="margin-right:0.13889em;">T</span><span class="mord">.</span><span class="mord mathnormal">Hse</span><span class="mord mathnormal">t</span><span class="mord mathnormal" style="margin-right:0.07847em;">I</span><span class="mord mathnormal">ni</span><span class="mord mathnormal">t</span><span class="mord mathnormal">ia</span><span class="mord mathnormal" style="margin-right:0.01968em;">l</span><span class="mord mathnormal">De</span><span class="mord mathnormal">lt</span><span class="mord mathnormal">a</span><span class="mord mathnormal" style="margin-right:0.13889em;">T</span><span class="mord">.</span><span class="mord mathnormal" style="margin-right:0.08125em;">H</span><span class="mord mathnormal" style="margin-right:0.03588em;">v</span><span class="mord mathnormal">o</span><span class="mord mathnormal" style="margin-right:0.07153em;">lC</span><span class="mord mathnormal">o</span><span class="mord mathnormal">n</span><span class="mord mathnormal">t</span><span class="mord mathnormal">in</span><span class="mord mathnormal">u</span><span class="mord mathnormal">i</span><span class="mord mathnormal">t</span><span class="mord mathnormal" style="margin-right:0.03588em;">y</span><span class="mord">.</span><span class="mord mathnormal" style="margin-right:0.08125em;">H</span><span class="mord">‘‘‘</span><span class="mord cjk_fallback">并在</span></span></span></span>FOAM_SRC/finiteVolume/lnInclude 文件夹中创建指向这些文件的链接,因此该文件夹可用于 Make/options 以启用在求解器应用程序中包含共享文件。默认情况下,所有 OpenFOAM 应用程序都包含finiteVolume/lnInclude 作为编译器的搜索目录:
```bash
EXE_INC = \
-I$(LIB_SRC)/finiteVolume/lnInclude \
此目录包含指向finiteVolume 目录及其子目录中所有头文件的符号链接。因此,来自 cfdTools 的不同应用程序之间共享的包含头文件默认可供任何 OpenFOAM 应用程序使用。
上面列出了根据头文件实现的其他全局可用功能,它们包括以下内容:
- 基于 CFL 条件的时间步调整
- 体积守恒校正
- 连续性误差的确定
- 读取重力加速度矢量…
有人可能会争辩说,根据包含在应用程序(求解器)代码中的文件实现的计算并不是一种纯粹的面向对象的软件设计方法。这是真的,然而,CFD 模拟的本质是程序性的:处理模拟输入以计算近似解并存储输出。因此,一些变量已成为全局变量,因此求解过程始终可以访问,例如场和网格。在这种情况下,将包含文件中定义的操作封装到类中并对其施加层次结构仍然是可能的。例如,没有什么能阻止用户实现类的层次结构,这些类实现不同的策略来修改基于 Courant 数的时间步长。实际上,使用全局字段变量作为参数执行的计算可以很好地封装到函数对象中,如第 12 章所述。然而,这种封装并非总是必要的,在这些情况下,使用包含的源文件。
fvVectorMatrix UEqn
(
fvm::ddt(rho, U)
+ fvm::div(rhoPhi, U)
+ turbulence-> divDevRhoReff(rho, U)
);
OOD 用于封装离散算子所需的插值等内容,并使它们的交互对 OpenFOAM 的用户不可见,除非作为配置文件中的命名条目。正如前面章节中已经指出的,fvSolution 和 fvSchemes 字典负责控制数值方案和求解器。数学模型的方程调用诸如速度、压力、动量等领域的离散算子。这就是为什么不同的求解器在 fvSolution 和 fvSchemes 字典中需要不同的条目的原因,如果默认条目设置为none的话。因此,求解器的用户和开发人员都不必关心任何方案是如何实现的,OpenFOAM 会根据配置文件中的规范自动选择所选方案。由于为格式启用了 RTS,因此如果离散化发生更改,则不得重新编译求解器。
提示:OpenFOAM 使用通用编程来实现离散微分算子。算子将离散化和插值操作分别分配给离散化和插值方案的通用层次结构。插值/离散化类模板已实例化,并已在运行时可选。结果,选择不同的格式时,不需要更改求解器代码。
9.1.1 Fields
如第 1 章所述,非结构化 FVM 需要将流域离散细分为有限体积的网格,物理场(例如压力、速度、温度)映射到该网格上。物理场、网格和解控制(由 Time 类实现)在模拟开始但时间循环开始之前由解算器初始化。可以在主求解器应用程序文件 interFoam.C 中检查求解器代码的初始化部分,如清单 32 所示。上面列出的大多数包含(头)文件都可以全局使用。一些头文件是求解器特定的,在这种情况下,它们对任何应用程序都不可用,但存储在求解器源目录中。求解器特定文件的示例是 createFields.H 和 readTimeControls.H,它们读取求解器特定字段和求解器相关控制结构。当调用求解器时,求解器期望在 createFields.H 中初始化的任何字段都存在于模拟案例的初始 (0) 目录中。
#include "setRootCase.H"
#include "createTime.H"
#include "createMesh.H"
pimpleControl pimple(mesh);
#include "initContinuityErrs.H"
#include "createFields.H"
#include "readTimeControls.H"
#include "correctPhi.H"
#include "CourantNo.H"
#include "setInitialDeltaT.H"
9.1.2 求解算法
动量守恒方程包含右侧的项,用于模拟作用在流体上的压力的体积力密度。压力场在模拟开始时是未知的。作用在流体上的压力会强制改变动量,但质量守恒(连续性)方程需要始终满足。对于不可压缩的流动,这种情况会导致连续性方程和动量方程之间的紧密耦合。这种方程耦合通常被称为压力-速度耦合,在 CFD 中开发了许多算法,其唯一目的是在处理方程耦合的同时保持求解过程稳定。
耦合可以通过使用块耦合求解器的代数方程组的联立求解来解决。研究非结构化网格的块耦合求解算法的起点通常是 [2] 的工作。专门针对 OpenFOAM 的开发是 [1] 和 [5] 等。尽管对方程耦合的强性质很直观,但由于在 CFD 中遇到压力-速度耦合问题时计算机的内存限制过高,这种方法在历史上并未被使用。因此,已经开发了将原始方程组修改为允许每个方程单独求解的分离算法。
有关压力-速度耦合的 CFD 求解算法的详细信息,请参见 [3] 和 [6] 所著的 CFD 教科书。 OpenFOAM 实现了两种主要的压力-速度耦合算法:最初由 [4] 开发的带有算子分裂的压力隐式 (PISO) 算法和最初由 [7] 开发的压力关联方程的半隐式方法 (SIMPLE) 算法。
大多数求解器定制涉及以一种或另一种方式修改数学模型方程。可能会引入全新的模型方程,方程项可能会因为它们对解的影响被忽略而被删除,并且可以添加新项,例如作用于流体的新力。虽然不可能涵盖自定义求解器过程中可能出现的所有复杂性和困难,但本章涵盖的一些示例应该有助于理解与求解器自定义相关的问题以及如何克服这些问题。求解器的一个典型修改是添加被动传输场和材料属性。求解器应用程序必须从模拟案例中读取新的场变量及材料属性。模拟案例中有各种可用的文件,从中读取不同类型的数据。让我们从涉及的一个更基本的操作开始:在字典中查找一个值。 OpenFOAM 配置(字典)文件和它们所基于的数据结构都在第 5 章中进行了详细描述。不过,本章还提供了使用字典的基本信息,以使求解器自定义描述更加自我持续。
9.2.1 使用字典
OpenFOAM 配置文件称为字典(字典文件),用于为求解器应用程序提供配置参数。在各种字典(例如 transportProperties、controlDict 或 fvSolution)之间,用户可以完全控制求解器、材料属性、时间步长等。在本节中,将介绍访问现有字典和新字典以及查找值并将其加载到求解器范围内。检查 icoFoam 求解器如何从 constant/transportProperties 字典中查找材料属性将作为如何处理字典的简单示例。首先,打开位于 FOAM_SOLVERS/incompressible/icoFoam/createFields.H 的 createFields.H 文件。在这个头文件的开头,有一个 IOdictionary 对象的实例,如下所示。IOobject 声明被注释掉以表明每个参数的用途。本节稍后将提供有关这些论点的更多详细信息。清单 33 的代码将字典初始化为全局变量,因此从中检索值仍然很简单。
Info<< "Reading transportProperties\n" << endl;
IOdictionary transportProperties
(
IOobject
(
// Name of the file
"transportProperties",
// File location in the case directory
runTime.constant(),
// Object registry to to which the dict is registered
mesh,
// Read strategy flag: read if the file is modified
IOobject::MUST_READ_IF_MODIFIED,
// Write strategy flag: do not re-write the file
IOobject::NO_WRITE
)
);
createFields.H 文件的接下来几行包含使用 transportProperties 字典中包含的值初始化粘度 (nu) 的代码:
nu 0.01;
预定义尺寸集dimViscosity用于设置运动粘度nu的单位量纲。
dimensionedScalar nu
(
"nu",
dimViscosity,
transportProperties
);
量纲标量的构造由构造函数完成:
dimensioned<Type> ::dimensioned<Type>
(
const word&,
const dimensionedSet&,
const dictionary&
)
有关 OpenFOAM 中量纲系统如何工作的更多信息,请参阅第 5 章。以下示例显示了 interFoam 求解器如何查找输运属性,这有点复杂。重要的源代码位于 FOAM_APP/solvers/multiphase/interFoam/ 在 createFields.H 文件的开头,实例化了 immiscibleIncompressibleTwoPhaseMixture 类(参见下面的代码片段)。有两个成员函数(rho1()、rho2()),用于查找twoPhaseMixture类的材质属性。检查类源代码是必要的,以便找到执行实际字典访问的代码。
Info<< "Reading transportProperties\n" << endl;
immiscibleIncompressibleTwoPhaseMixture mixture(U, phi);
volScalarField& alpha1(mixture.alpha1());
volScalarField& alpha2(mixture.alpha2());
const dimensionedScalar& rho1 = mixture.rho1();
const dimensionedScalar& rho2 = mixture.rho2();
9.2.2 对象注册及regIOobjects
由于物理场和网格在 OpenFOAM 求解器应用程序中以全局变量的形式使用,因此跟踪所有物理场和显式分配对其成员函数的调用将涉及大量不必要的代码重复。这种集群调用调度的一个示例是求解器请求将所有物理场写入硬盘。在直接使用对象的情况下,对象的名称将被硬编码,并且更改名称会在应用程序代码中引入一连串的更改。此外,实现此类调用的代码需要复制到多个位置。例如,负责物理场输出的相同代码随后将被复制到依赖于具有相同变量名称的同一组物理场的每个应用程序。对于依赖相同物理场变量的求解器系列,可以使用第 9.1 节中介绍的包含头文件。但是更改单个物理场变量会导致这样的头文件无法用于整个求解器系列。因此,这种方法代表了僵硬的软件设计,或者不能很好地扩展的软件设计。僵硬或不可扩展的软件设计是一种设计,其中单个扩展需要修改现有代码,此外,修改经常发生在现有代码库的多个位置。
由于这个问题,多个对象的操作协调背后的逻辑被封装到一个类中,然后可以在 OpenFOAM 代码的许多地方重用。为此,已经实现了一个对象注册表:一个对象将其他对象注册到自己,然后将对其成员函数的调用分派(转发)到已注册的对象。对象注册是 OOD 中观察者模式的一个实现,它在 8.4 节中有更详细的描述。此外,在 OpenFOAM Wiki 页面 1 上对对象注册表以及已注册的对象类进行了很好的审查。
使用对象注册表的一个例子是边界条件实现,其中在一个字段上操作的边界条件需要访问另一个字段。总压边界条件 (totalPressureFvPatchScalarField) 就是这样一个边界条件,需要访问多个字段才能更新分配给它的字段。
void Foam::totalPressureFvPatchScalarField::updateCoeffs()
{
updateCoeffs
(
p0(),
patch().lookupPatchField<volVectorField, vector> (UName())
);
}
练习:找出要使用的 totalPressureFvPatchScalarField 边界条件是什么。哪个成员函数执行实际计算?如何实施替代计算?您能想到替代计算的替代运行时可选实现吗?
总压力边界条件使用清单 36 中所示的 updateCoeffs 成员函数更新已分配给它的场,就像 OpenFOAM 中的所有其他边界条件一样。但是,updateCoeffs() 将计算分派给重载的 updateCoeffs。清单 36 中显示的 updateCoeffs 调用的第二个参数使用 patch() 成员函数访问边界字段的 fvPatch 常量引用属性。另一方面,fvPatch 类存储对有限体积网格的常量引用,它继承自 objectRegistry,因此是一个对象注册表。 lookupPatchField 被定义为 fvPatch 类模板的模板成员函数,在文件 fvPatchFvMeshTemplates.H 中,如清单 37 所示。函数的返回类型声明取决于模板参数 GeometricField,因此需要 typename 关键字,为了让编译器知道 PatchFieldType 确实是一种类型。成员函数模板中更重要的部分是显然利用了对象注册功能的返回语句,它是从对象注册类objectRegistry继承到fvMesh的。由于 fvPatch 是一个类模板,因此对基类成员函数的调用有点复杂。 lookupObject 是 objectRegistry 基类的成员函数模板,必须在成员函数调用站点使用 template 关键字指定。回顾所有 C++ 模板代码,有限体积网格边界补丁访问整个边界网格,然后访问相应的体积网格,并要求体积网格查找具有特定名称(名称)的字段。此示例中描述的通过所涉及类的调用路径允许总压力边界条件根据字段名称参数从网格访问字段。
template<class GeometricField, class Type>
const typename GeometricField::PatchFieldType&
Foam::fvPatch::lookupPatchField
(
const word& name,
const GeometricField*,
const Type*
) const
{
return patchField<GeometricField, Type>
(
boundaryMesh().mesh().objectRegistry::template
lookupObject<GeometricField> (name)
);
}
在本节中,通过在 interFoam 求解器中添加一个新的 PDE 来实现一个新的求解器,以模拟两个不可压缩的不混溶流体相。 PDE 及其支持代码的目的是展示如何执行实现,而不是模拟真实的物理传输过程。流体界面上和跨流体界面的传输现象建模需要仔细和严格的推导。在大多数情况下,该等式源于 compressibleInterFoam 求解器中可用的实现。在那里,由于使用了耦合压力、温度和密度的状态方程,因此考虑了跨界面的热传递。为简单起见,热力学状态方程被省略,假设为层流。
9.3.1 附加模型方程
作为层流两相流中非定常被动标量输运模型的示例,使用以下等式 其中 表示温度, 是密度, 是速度,是相混合物的导热系数。
interFoam 求解器在单场公式中实现两相 Navier-Stokes 方程,以模拟两个不可混溶的不可压缩流体相的两相流。该模型通过引入额外的标量(体积分数场)来区分流体相,将两种不混溶流体相的流动描述为单个连续体的流动。关于两相流建模的更多信息可以在 [8] 的书中找到。
任何具有介于两者之间的 α 值的单元都被视为界面单元,其材料特性加权为两个主要相的混合物,因为 α 定义为体积分数 其中 V1 是总体积为 V 的单元中phase 1 所占的体积。然后使用体积分数场对单个连续体的特性进行建模,形成混合物量,例如混合物粘度 或混合密度: 其中 ν1, ν2 和 ρ1, ρ2 分别是两个流体相的运动粘度和密度。方程 9.1中Deff 中的有效热传导系数在本例中以类似方式建模,使用 α1 场 这里,和代表各个流体相的传导系数和比热容。
由方程 9.5 建模的热传导系数基于体积分数场,其方式与其他相属性类似。以这种方式使用体积分数物理场值,为此示例将物理属性的恒定值分配给两个流体相的主体区域。流体界面的区域将具有区间 [0, 1] 内的 α1 值,因此将定义相应相属性的两个恒定值之间的过渡区域。过渡区轮廓的形状将由描述混合特性的模型的性质决定,如传导系数(见方程 9.5)。这种方法如何准确地应用于跨移动界面的热传递的实际物理问题对于描述如何在 OpenFOAM 中执行求解器修改并不重要,因此不在范围之内。
9.3.2 准备求解器进行修改
在更改现有求解器的源代码之前,必须创建求解器应用程序的新副本。将 interFoam 求解器的源代码目录复制到个人应用程序目录并重命名:
cp -r $FOAM_SOLVERS/multiphase/interFoam/ $FOAM_RUN/../applications/
cd $FOAM_RUN/../applications/
mv interFoam heatTransferTwoPhaseSolver
cd heatTransferTwoPhaseSolver
mv interFoam.C heatTransferTwoPhaseSolver.C
提示:每个 OpenFOAM 版本都为用户工作目录导出
$FOAM_RUN变量,但在 OpenFOAM 安装期间不会生成它。如果此目录不可用,可以使用mkdir -p $FOAM_RUN创建它。
在接下来的步骤中,必须删除所有不需要修改的文件。这样做是为了防止代码重复,应始终避免。如果代码重复,那么维护求解器就会出现问题,因为随着 OpenFOAM 的发展,求解器文件需要更新。这就是为什么在实施求解器时对现有文件的更改应保持在最低限度。
提示:在开发新的求解器时,将共享文件中引入的更改保持在最低限度。在重用现有文件的同时引入其他文件并将它们包含到新的求解器应用程序中,使新求解器更易于维护,因为重用现有文件将在新的 OpenFOAM 版本中获取这些文件中的更改。
应该从目录中清除所有未更改的文件:
rm -rf interMixingFoam/ overInterDyMFoam/
rm alphaSuSp.H createFields.H correctPhi.H initCorrectPhi.H rhofs.H pEqn.H UEqn.H
提示:如果从一开始就知道必须修改哪些求解器文件,则只需复制这些文件和 Make 目录。
由于求解器源代码文件已重命名,因此必须修改 Make/files 以反映更改。 Make/files 配置文件应仅包含此处显示的行:
heatTransferTwoPhaseSolver.C
EXE = $(FOAM_USER_APPBIN)/heatTransferTwoPhaseSolver
让 wmake 构建系统知道要从重命名的求解器源代码文件中构建并安装在用户应用程序二进制目录中的可执行应用程序。因此,这将指示 wmake 编译文件 heatTransferTwoPhaseSolver.C 及其依赖项,并创建一个名为 heatTransferTwoPhaseSolver 的可执行求解器。此时调用 wmake 会失败:我们已经删除了方程文件、场初始化等,最终得到
ls
heatTransferTwoPhaseSolver.C Make
为了通知新求解器重新使用来自 interFoam 的文件和来自 (FOAM_SOLVERS)/multiphase/interFoam
-IFOAM_SOLVERS/multiphase/VoF `以查找与 VoF 求解器系列共享的文件。
此时,可以使用 wmake 构建新的 heatTrasnferTwoPhaseSolver,它的行为与 interFoam 完全相同。
9.3.3 添加温度场和热传导系数
必须从transportProperties字典中为每个相查找两个新的所需材料相属性:热传导系数$k$和比热容 $C_v$。此外,需要初始化新的温度 $T$ 和有效传热系数 $D_{eff} $。初始化被放置在一个新的初始化文件 createHeatTransferFields.H 中,连同温度和传热系数的初始化,如下面的代码段 所示。代码段所示的新 createHeatTransferFields.H 应插入到新求解器中 createFields 之后.H 文件,在 immiscibleIncompressibleTwoPhaseMixture 被初始化之后。类型 dimensionedScalar 的热容量将从 transportProperties 字典文件中每个阶段的子字典中加载。完成所有字典查找和声明后,新模型方程 9.1 将被添加到求解算法中。
const dictionary& phase1dict = mixture.subDict ("phase1");
const dictionary& phase2dict = mixture.subDict ("phase2");
auto k1 (phase1dict.get<dimensionedScalar> ("k"));
auto Cv1 (phase1dict.get<dimensionedScalar> ("Cv"));
auto k2 (phase2dict.get<dimensionedScalar> ("k"));
auto Cv2 (phase2dict.get<dimensionedScalar> ("Cv"));
volScalarField T
(
IOobject
(
"T",
runTime.timeName(),
mesh,
IOobject::MUST_READ,
IOobject::AUTO_WRITE
),
mesh
);
volScalarField Deff
(
"Deff",
(alpha1*k1/Cv1 + (1.0 - alpha1)*k2/Cv2)
);
9.3.4 编写温度方程
温度方程放置在单独的文件 TEqn.H 中,然后该文件包含在求解器应用程序中。 TEqn.H 文件中定义的代码实现了两个操作。它计算系数 Deff 并求解方程 9.1 给出的被动温度传递 PDE。
Deff 系数计算为基于单元中心 alpha1 值(公式 9.5)的线性加权平均值。对于这个例子,计算 Deff 系数的方法与 compressibleInterFoam 求解器中使用的方法相同。由于 Deff 系数会因单元而异,因此它被实现为 volScalarField,而不是单个标量。在 createHeatTransferFields.H 中初始化扩散系数字段后,可以如下所示实现传输方程。
Deff == alpha1*k1/Cv1 + (1.0 - alpha1)*k2/Cv2);
solve
(
fvm::ddt(rho, T)
+ fvm::div(rhoPhi, T)
- fvm::laplacian(Deff, T)
);
现在 TEqn.H 已完成,需要将其添加到在主求解器应用程序文件 heatTransferTwoPhaseSolver.C 中实现的求解算法中. TEqn.H 应该插入到内部 PIMPLE 循环的上方,与下面代码段所示的动量方程相邻。
while (pimple.loop())
{
...
mixture.correct();
if (pimple.frozenFlow())
{
continue;
}
#include "TEqn.H"
#include "UEqn.H"
...
}
这样就完成了将热传递方程添加到 interFoam 求解器的求解算法所需的源代码修改。应该从构建过程生成的旧文件中清理求解器目录,然后编译求解器应用程序:
wclean
wmake
完成新求解器后,需要设置与新求解器兼容的模拟案例。
9.3.5 设置案例
提示:最终案例设置可以在案例存储库中找到,位于 chapter09/2DheatXferTest 文件夹中。
创建新求解器后,现在需要新的初始条件、边界条件、材料属性和求解器控制输入参数来处理传热计算。在0文件夹下,温度场以T文件的形式添加,其必须具有合适的量纲:
FoamFile
{
version 2.0;
format ascii;
class volScalarField;
location "0";
object T;
}
dimensions [0 0 0 1 0 0 0];
应该设置边界条件,在这个例子中我们简单地使用零梯度边界条件。要为新的温度场设置初始条件,需要编辑系统目录下的 setFieldsDict 文件。在本例中,我们将上升气泡的温度设置为高于其环境的值:
defaultFieldValues
(
volScalarFieldValue alpha1 0
volVectorFieldValue U (0 0 0)
volScalarFieldValue T 300
);
regions
(
sphereToCell
{
centre (1 1 0);
radius 0.2;
fieldValues
(
volScalarFieldValue alpha1 1
volScalarFieldValue T 500
);
}
);
还应修改constant目录中的 transportProperties 文件,为每个相添加 k 和 Cv 系数值。我们任意选择了这些值:
e1
transportModel Newtonian;
nu nu [ 0 2 -1 0 0 0 0 ] 1e-02;
rho rho [ 1 -3 0 0 0 0 0 ] 100;
k k [ 1 1 -3 -1 0 0 0] 100;
...
e2
transportModel Newtonian;
nu nu [ 0 2 -1 0 0 0 0 ] 1e-02;
rho rho [ 1 -3 0 0 0 0 0 ] 100;
k k [ 1 1 -3 -1 0 0 0] 100;
Cv cv [ 0 2 -2 -1 0 0 0] 100;
...
由于向求解器添加了新的 PDE,因此应在 system/fvSchemes 中为其微分算子选择离散化方案,以防未提供或不适用默认选项。在此示例中,默认 CDS(高斯线性)方案将替换为迎风方案:
divSchemes
{
default Gauss linear;
div(rho*phi,U) Gauss limitedLinearV 1;
div(rho*phi,T) Gauss upwind;
最后,应设置涉及温度方程离散化得到的线性系统解的参数。 将TFinal 添加到 fvSolution 文件中,例如
TFinal
{
solver PBiCG;
preconditioner DILU;
tolerance 1e-06;
relTol 0;
}
这些是设置传热方程求解器及其参数的选项。这应该是运行带有新模型方程的新求解器所需的最后一个案例配置更改。求解器可以在案例目录中运行,并且可以分析模拟的结果。
9.3.6 执行求解器
为了运行案例,请确保示例代码库的库和应用程序代码通过调用自动编译:
./Allwmake
在示例代码存储库的主目录中。要启动求解器,只需在仿真案例目录中执行以下命令:
heatTrasferTwoPhaseSolver
图 9.1 显示了用于模拟二维上升气泡的体积分数场 α 和温度场 T 的分布。气泡温度设置为高于周围流体的温度,这将导致气泡在上升时向其周围释放热通量。
不同几何形状的热传导存在精确解,例如实心圆柱体或板。为一个被热静止空气包围的圆柱体或两个接触的板创建一个模拟案例,并验证新的求解器。解是否收敛到精确解?
- I Clifford and H Jasak. “The application of a multi-physics toolkit to spatial reactor dynamics”. In: International Conference on Mathmatics, Computational Methods and Reactor Physics. 2009.
- M Darwish, I Sraj, and F Moukalled. “A coupled finite volume solver for the solution of incompressible flows on unstructured Grids”. In: Journal of Computational Physics 228.1 (2009), pp. 180–201.
- J. H. Ferziger and M. Perić. Computational Methods for Fluid Dynamics. 3 rd rev. Ed. Berlin: Springer, 2002.
- R. I. Issa. “Solution of the implicitly discretised fluid flow equations by operator-splitting”. In: Journal of Computational physics 62.1 (1986), pp. 40–65.
- Kathrin Kissling et al. “A coupled pressure based solution algorithm based on the volume-of-fluid approach for two or more Immiscible fluids”. In: V European Conference on Computational Fluid Dynamics, ECCOMAS CFD. 2010.
- Suhas Patankar. Numerical heat transfer and fluid flow. CRC Press, 1980.
- S.V. Patankar and D.B. Spalding. “A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows”. In: International Journal of Heat and Mass Transfer 15.10 (1972), pp. 1787–1806.
- G. Tryggvason, R. Scardovelli, and S. Zaleski. Direct Numerical Simulations of Gas-Liquid Multiphase Flows. Cambridge University Press, 2011. Isbn: 9780521782401.
在本章中,我们将深入了解非结构有限体积法(FVM)。第2章介绍了非结构化网格的详细信息,第1.3节总结了非结构化FVM。本章介绍了OpenFOAM模拟中边界条件的使用及其进一步发展。
在 FVM(参见第 1.3 节)中,当使用隐式方法离散化模型方程时,每个网格都会生成一个代数方程。线性方程组的系数由非结构化网格的连通性和插值格式(system/fvSchemes 字典)决定。如果该面属于域边界,则应用边界条件,因为该面只有一个相邻的内部网格,因此没有任何内容可以从另一侧进行插值。没有边界条件,就无法确定边界上的面心值,也无法完成线性系统。
在有限体积网格中,每个边界面属于一个边界面片(边界面的集合),每个边界面片被定义为某种类型(参见第 2 章)。因此,边界网格是一组边界块。边界patch的类型确实限制了所有流场的边界条件的选择,但它本身并不是一个边界条件。第 2 章概述了不同的边界类型。
OpenFOAM 案例中的任何字场文件都包含两个不同的部分:内部场和边界场。 boundaryField 描述了边界上的值(边界Patch)是如何指定的,而 internalField 对体积中心值的作用相同。其他几何场(点场和面场)边界上的值以类似的方式确定。第 2 章和 [2] 中提供了边界场操作的详细信息。
在详细介绍如何在 OpenFOAM 中实现边界条件之前,本节将介绍从用户的角度定义边界条件的过程。
10.2.1 内部、边界和几何场
计算区域的边界和相应的边界patch可以在 constant/polyMesh/boundary 文件中找到。每个边界patch都是一组单元(有限体积)面。 OpenFOAM 用户很少检查边界文件;它可能有助于程序员理解 OpenFOAM 用于存储非结构化网格的连接性的数据结构。
OpenFOAM 将物理场作为文件存储在初始时间步目录 (0文件夹) 中。例如,考虑案例rising-bubble-2D的动态压力场p_rgh的配置文件的一部分:
internalField uniform 0;
boundaryField
{
bottom
{
type zeroGradient;
}
internalField 关键字与存储在网格中心的值相关(值为 0 的均匀场),bottom边界条件定义为 zeroGradient 类型(参见第 1 章的数值描述)。
OpenFOAM 操纵与非结构化网格的不同元素相关联的张量场。例如,速度 U 的 volVectorField 和压力场 p 的 volScalarField 与单元中心相关联,而 surfaceScalarField 存储与面中心相关联的体积通量场 phi。对任何求解器的简要介绍显示了在这些场上执行的许多不同操作。为了说明几何场上的一些常见操作,volScalarField p 作为示例的来源:
访问场值只需将特定的网格标签传递给场的访问运算符 [](const label&) 即可。在本例中,我们选择单元格 4538:
const label cellI{4538};
Info << p[cellI] << endl;
访问边界上的值稍微复杂一些,因为 volScalarField 不直接在网格面上存储任何值。边界值由在特定边界上定义的边界条件确定。可以使用以下代码来计算网格第一个边界块上 p 的最大值:
const label boundaryI{0};
Info << "max(p) = " << max(p.boundaryField()[boundaryI]) << endl;
提示:边界patch在边界网格中的存储顺序对于所有场都是相同的,并且由patch在 polyMesh/boundary 文件中列出的方式决定。这又由使用的网格生成器确定。
默认情况下,当使用访问运算符 operator[](const label&) 访问时,任何场都会从其 internalField 返回值。要访问边界字段的值,必须调用boundaryField() 成员函数(用于常量访问的boundaryFieldRef())。这将返回一个边界补丁列表,每个网格边界都有一个边界补丁。每个元素都是用户为此补丁选择的边界条件的抽象表示。根据物理场的类型,这种表示要么继承自 fvPatchField 要么继承自 pointPatchField,尽管第一种是最常用的。
提示:在使用OpenFOAM中的类时,查看Extended Code Guide有助于查找哪些成员函数可用以及它们的接口。
如上例所示,OpenFoam实现了所谓的geometrical场,它将值分成两组:内部值和边界值。 几何物理场是OpenFoam中的类模板,因为它们存储不同级别的张量,并将它们与不同的网格单元相关联。 例如,如果我们想象一个由线段组成的几何网格,并将其称为线网格,那么与线网格一起工作的几何场概念的相应模型将被命名为线场。 线场将张量值映射到每条线的中心(内部场值),以及线网格的两个边界端点(边界场值)。 实现几何场概念的类模板被命名为geometrical,它的实例化产生不同的几何场模型,映射到不同类型的网格。 在OpenFoam中,有不同的几何物理场模型:
- 第一类是众所周知的物理场,如
volScalarField和volVectorField,它们将数据存储在网格中心。 在边界上,必须将边界条件应用于存储在面中心的模拟值。 满足vol*field的命名约定。 - 第二类是在面中心存储网格每个面的物理场。这不限于域的边界。其中一种场类型是surfaceScalarField,用于定义两个相邻单元之间的通量。此类的所有场均命名为
surface*Field。 - 第三类包含
pointScalarField或pointVectorField类型。 当谈到OpenFOAM物理场:将数据存储在网格点中的物理场时,这一类的物理场可能会被忽略。 网格中的每个点都有它自己的值,在边界上,必须为边界上的点定义边界条件,而不是为面中心定义边界条件。 在源代码中查找point*Field将显示该类别的所有物理场。
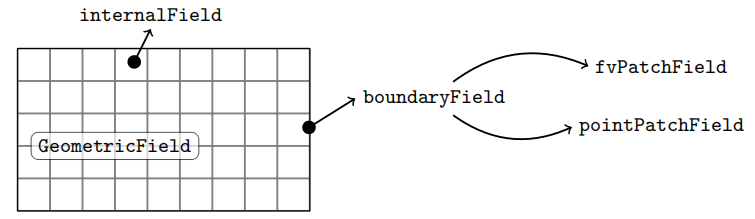
在此澄清之后,我们可以潜入物理场与边界条件之间的关系。 从设计角度来看,OpenFoam中的边界条件封装了映射到域边界的场值,以及负责基于内部值--边界条件--确定这些边界值的计算的成员函数。 GeometricField类模板提供了成员函数,简化了边界条件的制定和更新。 成员函数的一些功能包括计算边界物理场值和将存储在相邻内部单元中的值作为参数。 两者都是实现任何边界条件的关键要求。 关于哪些成员函数应该执行哪些任务的更多信息将在下一节10.2.2中提供。 边界物理场--因此边界条件与内场一起封装,形成几何场(见图10.1)。 三个几何场模型中的任何一个,都是具有适当模板参数的GeometricField的typedef。
// 程序清单41
template<class Type, template<class> class PatchField, class GeoMesh>
class GeometricField
:
public DimensionedField<Type, GeoMesh>
{
可以在源代码中研究边界条件的结构。例如,考虑清单41所示的GeometricField类模板的声明部分。从清单41中可以明显看出,GeometricField是从DimensionedField派生出来的。这意味着在GeometricField类模板(几何字段模型)的任何实例化上执行的任何默认算术运算都将在不包括边界的情况下执行。这是有意义的,因为边界上的值应该仅由相应的边界条件确定。使用附加的赋值运算符GeometricField::operator ==,运算被扩展为也考虑边界场。边界上的值可以从实际边界条件的外部覆盖,直到GeometricField::correctBoundaryConditions()成员函数再次计算边界条件。
从类派生(在上面的代码片段中是:public)会导致继承其成员函数。 对于GeometricField,算术运算符继承自DimensionedField。 由于边界物理场是由GeometricField和GeometricBoundaryField属性组成的,所以维度对内部场值进行建模。 因此,来自维度的重载算术运算符排除边界场值。
注:运算符GeometricBoris::Operator==不是OpenFoam中的逻辑相等比较运算符,它扩展了GeometricalField的赋值,以包括边界场值。 它被添加到GeometricField界面中,以包括合成边界物理场上的算术运算。
边界场本身声明为嵌套类模板,GeometricField将其存储为私有属性。 边界场类模板被命名为GeometricBoundary,它的声明在GeometricField类模板中可以找到,其包含一个边界patch物理场列表,每个网格边界一个patch场。 虽然GeometricBoundaryField封装在GeometricField中,但提供了一个非常量访问,这导致GeometricField的客户端代码能够更改边界物理场的值。 乍一看,这打破了几何场对边界物理场的封装,然而好处超过了设计原则,因为这种方法产生了更大的使用灵活性。 例如,热力学模型可能以依赖于另一个几何场的方式改变场值。 这种情况下的变化是由几何场以外驱动的,这通常是这种情况,因为几何物理场是OpenFoam中的全局变量,由求解器操作,该求解器被实现为计算的过程序列。 对边界场数据成员的非常量访问如清单42所示。
//程序清单42
Boundary& boundaryFieldRef(const bool updateAccessTime = true);
//- Return const-reference to the boundary field
inline const Boundary& boundaryField() const;
与边界场相比,在GeometricField中内部场的处理方式不同。由于GeometricField派生自DimensionedField,因此不需要返回不同的对象。要访问内部场,将返回对 *this的引用,因为DimensionedField通过维度检查实现内部场及其算术运算。清单43阐明了几何字段如何提供对内部字段的访问。internalField()成员函数返回对GeometricField的非常数引用,该引用通过继承是DimensionedField。
// 程序清单43
// GeometricField.H
//- Return internal field
InternalField& internalField();
// GeometricField.C
template
<
class Type,
template<class> class PatchField,
class GeoMesh
>
typename
Foam::GeometricField<Type, PatchField, GeoMesh> ::InternalField&
Foam::GeometricField<Type, PatchField, GeoMesh> ::internalField()
{
this-> setUpToDate();
storeOldTimes();
return *this;
}
此时,您应该对OpenFoam中的模拟所涉及的物理场有了一个概述,以及为什么GeometricBoundaryField被封装在GeometricField中,并为GeometricField类模板的客户机代码所做的操作准备了非常量访问。 分析类继承和协作关系图虽然很有帮助,但在获得理解方面不如使用类本身有效,这将在下面几节中讨论。
10.2.2 边界条件
顾名思义,边界条件可为存储在边界场(GeometricBoundaryField)中的值添加功能。在面向对象设计(OOD)中,添加功能通常意味着扩展现有的类,这在边界条件的情况下也是如此。实际上,上述GeometricBoundaryField不仅封装存储在计算域边界的场值,每个物理场都用确定边界条件行为的虚拟成员函数来扩展。
边界条件是一个层次概念,在有限元法中,相似的边界条件被分成边界条件类别。 因此,为了使用户能够在运行时选择边界条件(RTS),它们被建模为类层次结构。顶级父抽象类fvPatchField定义每个边界条件必须符合的类界面。 OpenFOAM中的每个边界条件都是由fvPatchField或pointPatchField导出的。 后者多用于涉及网格运动或修改的应用。 两者都有一个名为internal_的常数私有属性,它是对GeometricField的内部场的引用,这在前一节中已经介绍过。 该属性提供对内部场值的访问,而不仅仅是对与边界网格贴片直接相邻的单元格的访问。 对于PointPatchField,interalField_属性声明为:
const DimensionedField<Type, pointMesh> & internalField_;
fvPatchField的内部场声明与fvPatchField相同,但是dimensionedField的第二个模板参数是volmesh而不是pointmesh:
const DimensionedField<Type, volMesh> & internalField_;
由于pointPatchField符合与fvPatchField相同的类接口,并且最常遇到体积场,因此本节将介绍fvPatchField。
在我们详细讨论fvPatchField的哪个成员函数是相关的之前,当涉及到新边界条件的实现时,我们尝试总结一下GeometricField和实际访问边界条件之间的联系。图10.2给出了这种关系的图示。几何场组成几何边界场,它继承自(FieldField),因此是(边界)场的集合。需要几何边界场的合成,因为内部场值的修改需要通过边界条件更新边界场值。此外,边界场不能被分离成与内部场不同的对象。内部场和边界场不仅在拓扑上通过网格彼此相连,当方程离散化以计算内部场值时,有限体积法需要边界场值。网格的细化导致单元面的分裂,因此内部场和边界场的长度在这种情况下也是间接连接的。因此,将内部场和边界场分开是毫无意义的。它将引入需要显式同步的全局变量,这将使应用程序级别上所有字段操作的语义严重复杂化。几何场在边界场的集合上循环,并且通过将更新委托给对应的边界条件来更新每个边界场。图10.2显示了PatchField模板参数,该参数在实例化时(体积网格的fvPatchField)是一个边界条件。
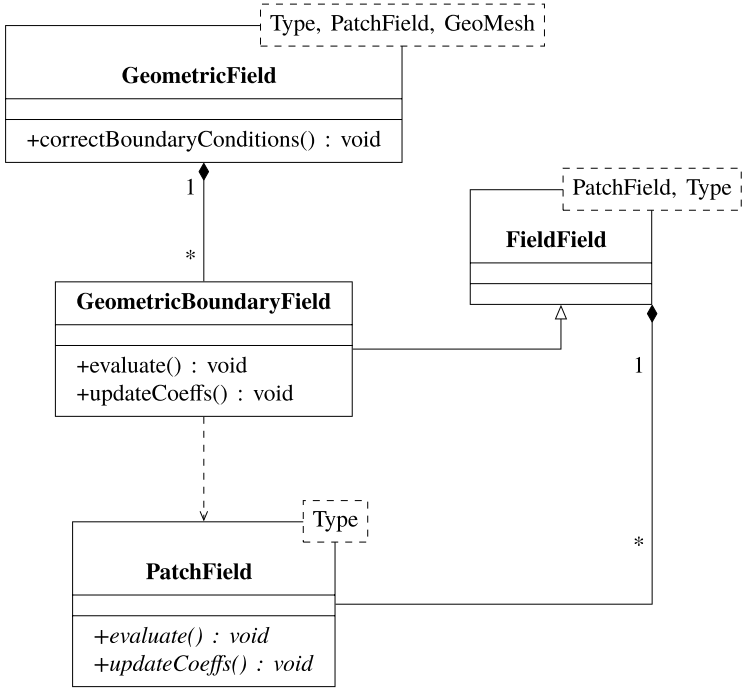
当内部场被修改并且边界条件将被更新时,OpenFOAM应用程序调用GeometricField的correctBoundaryConditions()成员函数:在求解器中为场求解PDE或在预处理应用程序中显式计算内部值之后。GeometricField::updateBoundaryConditions()成员函数的实现如清单44所示。
// 程序清单44
// Correct the boundary conditions
template
<
class Type,
template<class> class PatchField,
class GeoMesh
>
void Foam::GeometricField<Type, PatchField, GeoMesh> ::
correctBoundaryConditions()
{
this-> setUpToDate();
storeOldTimes();
GeometricBoundaryField_.evaluate();
}
注:要理解GeometricField如何更新边界条件,必须理解清单44中的最后一行。
清单44中的最后一行调用GeometricBoundaryField的成员函数evaluate(),该函数依次执行各种任务。如果边界条件尚未初始化,则此成员函数调用fvPatchField的成员函数initEvaluate(),否则会调用成员函数evaluate()。由于OpenFOAM实现了zero halo layer并行,因此并行通信由GeometricBoundaryField::evaluate()处理,因为进程边界也作为边界条件实现。
geometricBoundaryField::Updatecoeffs()成员函数是从客户端代码触发特定FvPatchField功能的另一个主要成员函数。 与evaluate())相比,updatecoeffs()的实现更短,因为没有实现并行通信。 清单45显示了GeometricBoundaryField::UpdatEcoeffs的实现。
//程序清单45
template<class Type,template<class> class PatchField,class GeoMesh>
void Foam::GeometricField <Type,PatchField,GeoMesh> ::GeometricBoundaryField::updateCoeffs()
{
if (debug)
{
Info<< "GeometricField<Type, PatchField, GeoMesh> ::"
"GeometricBoundaryField::"
"updateCoeffs()" << endl;
}
forAll(*this, patchi)
{
this-> operator[](patchi).updateCoeffs();
}
}
清单45中的forAll循环遍历GeometricBoundaryField的所有patch,称为 *this。fvPatchField的成员函数updateCoeffs()使用运算符[]直接为域边界的每个单元调用。
updateCoeffs()和evaluate()成员函数表示fvPatchField公共接口的相关部分,可从每个求解器自动访问该部分。这两个成员函数之间的主要区别是evaluate()可以在单个时间步长中调用任意次数,但只能执行一次。另一方面,updateCoeffs()不检查边界条件是否更新,它将执行与调用次数相同的计算。两者都是由基类fvPatchField提供的通用类接口的一部分,可用于对直接或间接从fvPatchField导出的自定义边界条件进行编程。
在正式发布中只有少数边界条件是直接从fvPatchField导出的,如基本的fixedValueFvPatchField和zeroGradientFvPatchField。大多数导出的边界条件直接继承自基本边界条件。mixedFvPatchField是一个流行的基类,它提供了在用户定义的固定值和固定梯度边界条件之间进行混合的功能。mixedFvPatchField的类协作关系图如图10.3所示。它包含三个新的私有属性,如清单46所示,并且它不依赖于固定梯度和固定值边界条件的实现。相反,规定的固定梯度和固定值边界物理场存储为字段类型的私有属性。
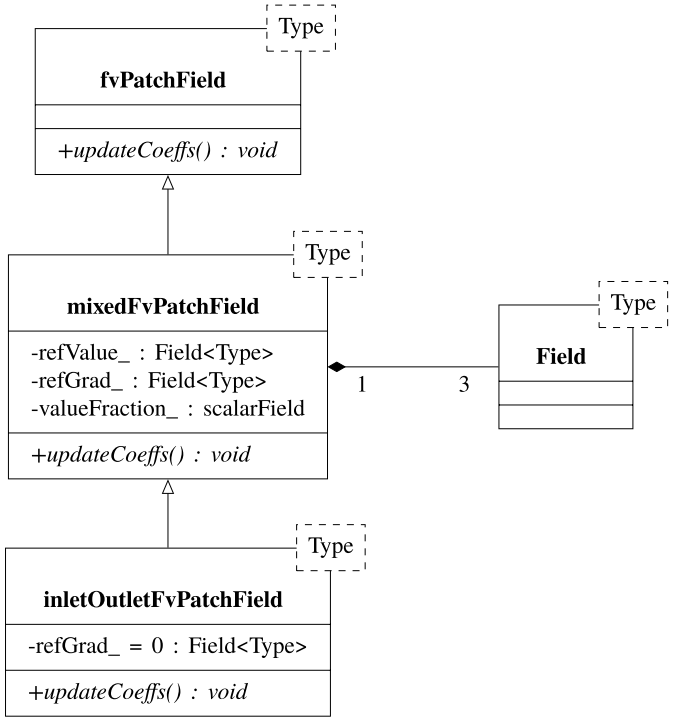
//程序清单46
//- Value field
Field<Type> refValue_;
//- Normal gradient field
Field<Type> refGrad_;
//- Fraction (0-1) of value used for boundary condition
scalarField valueFraction_;
因为这些属性是私有的,所以有公共成员函数提供对它们的常量和非常量访问。这使派生类能够间接使用属性,以便在固定值和零梯度边界条件之间实现不同的混合方式。直接从mixedFvPatchField导出的常用边界条件是inletOutletFvPatchField。它根据通量的方向在固定值和零梯度边界条件之间切换。如果通量指向域之外,则其充当零梯度边界条件(zeroGradientFvPatchField),否则其充当固定值边界条件(fixedValueFvPatchField)。这是在面对面的基础上并基于mixedFvPatchField边界条件的私有属性来确定的。场的梯度不是由用户在mixedFvPatchField中规定的-它由inletOutletFvPatchField构造函数设置为零值。
程序清单47中计算了mixedfvpatchfield<type> ::updatecoeffs()稍后使用的分数值,方法是为具有正(流出)容积流量的面赋值1,否则赋值0。 清单47显示了inletOutletFvPatchField的updatecoeffs())成员函数的实现。 这个成员函数只设置valueFraction()的值,边界场的计算被委托给父级mixedValueFvPatchField。 函数pos如清单48所示。 如果标量s的值大于或等于零,则返回1,否则返回0。 zeroGradientFvPatchField和fixedValueFvPatchField的实际赋值是通过调用mixedFvPatchField::updateCoeffs()完成的,因此不能重新实现。
//程序清单47
template<class Type>
void Foam::inletOutletFvPatchField<Type> ::updateCoeffs()
{
if (this-> updated())
{
return;
}
const Field<scalar> & phip =
this-> patch().template lookupPatchField
<
surfaceScalarField,
scalar
>
(
phiName_
);
this-> valueFraction() = 1.0 - pos(phip);
mixedFvPatchField<Type> ::updateCoeffs();
}
//程序清单48
inline Scalar pos(const Scalar s)
{
return (s > = 0)? 1: 0;
}
10.2.2.1 读取边界条件数据
在对可能具有新参数的自定义边界条件进行编程的过程中,需要从0目录中的场文件中读取相应的新参数名称和值。 因此,程序员必须在该文件中添加必要的参数及其值。 当边界条件以字典的形式从文件中读取时,字典将被读取并传递给边界条件构造函数。
某些边界条件可能使用dictionary类成员函数,该函数在提供默认值的同时查找数据。 在这种情况下,切换边界条件的类型和不提供适当的参数不会导致运行时错误。 Dictionary类上的操作在第5章已经讨论过,在下一节解释新边界条件的编程之前,应该很好地理解这些操作。
上一节概述了OpenFOAM中边界条件的实现。 在这一节中,描述了两个新的边界条件的植入。
OpenFOAM提供了大量不同的边界条件可供选择,并且在代码的这一部分也进行了社区开发,其中最突出的是swak4Foam贡献的groovyBC边界条件。在编写符合自身需求的新边界条件之前,明智的做法是查看代码库中是否已经提供了此功能,或者是否可以通过groovyBC边界条件进行建模。
关于如何在OpenFOAM中编写自己的边界条件,互联网上已经有相当多的信息。 本章中的例子是独立于现有材料编写的。 第一个例子展示了如何扩展OpenFOAM中任何边界条件的功能而不修改它,具体目的是减少边界处的再循环。第二个示例演示如何开发一个新的pointPatchField来将预定义的运动应用到patch。 这个预定义的运动是从必须由用户提供的表格数据中计算出来的。 这两个例子都强调了OpenFOAM中边界条件的根抽象基类所固定的类界面的正确使用,即fvPatchField和pointPatchField类。
10.3.1再循环控制边界条件
在本例中,介绍了如何在运行期间通过附加计算(功能)扩展现有边界条件的方法。假设有一个边界条件,在仿真执行时以某种方式更新边界值。在某个点,基于模拟结果,模拟的条件(例如,在另一边界处的压力)发信号通知附加的边界操作是必要的。发生这种情况时,新的延伸边界条件会在执行时间启用额外的计算,并相应地修改边界值。
一个很好的技术例子是充满理想气体的加热密闭容器。当热通量进入容器时,容器内的压力上升。扩展边界条件将测量容器盖处的压力,并且当压力达到特定值时打开盖。从数值上讲,该边界条件将在模拟过程中根据盖处的压力改变其类型,从封闭壁面改变为出口边界条件。
在本章中给出的例子中,再循环是在边界处测量的。 当再循环发生时,附加计算将边界条件的性质修改为流入条件。
注:再循环边界条件示例在并行执行中可能不起作用,这取决于修改的边界是否是处理器域的一部分。本例的目的是展示网格、对象注册表和物理场如何相互连接,而不是如何并行化边界条件更新。
假设只使用继承就可以实现这样的扩展。 然而,这将需要在OpenFOAM中扩展每个边界条件,以说明需要执行的启用RTS的额外计算。 通过使用多重继承来扩展每个边界条件将导致对现有边界条件的修改,只是为了考虑可能的扩展(即循环控制),这取决于用户的选择,可以在运行时使用,也可以不使用。 显然,这绝不是一个通用的方法,它使得在运行时不修改现有代码就很难实现扩展。 当一个新功能需要在运行时添加到一个已经存在的类层次结构中而不修改该层次结构的模型时,可以使用面向对象的设计模式装饰器模式。 关于decorator模式和其他OOD模式的细节在书中由[1]给出。 图10.4阐明了零次边界条件的工作原理,该边界条件是用任意函数修饰的。
10.3.1.1 使用decorator模式向BC添加功能
边界条件修饰器本身就是一个边界条件,因为它也修改边界场。 因此,装饰器继承自OpenFOAM中所有边界条件的fvPatchField抽象基类。 除了从fvPatchField继承之外,装饰器还组成它自己的基类(fvPatchField)的对象。
为了澄清这一点,图10.5中给出了应用于边界条件层次结构的装饰器模式的统一建模语言(UML)类协作图。 如图所示,装饰器和其他边界条件一样是类层次结构的一部分。 因此,对于OpenFOAM中的边界条件,使用抽象基类fvPatchField施加这样的IS-A关系可以使边界条件修饰器充当OpenFOAM客户端代码其余部分的边界条件。 这与普通继承的原理完全相同,只是扩展了存储继承的对象的实例。
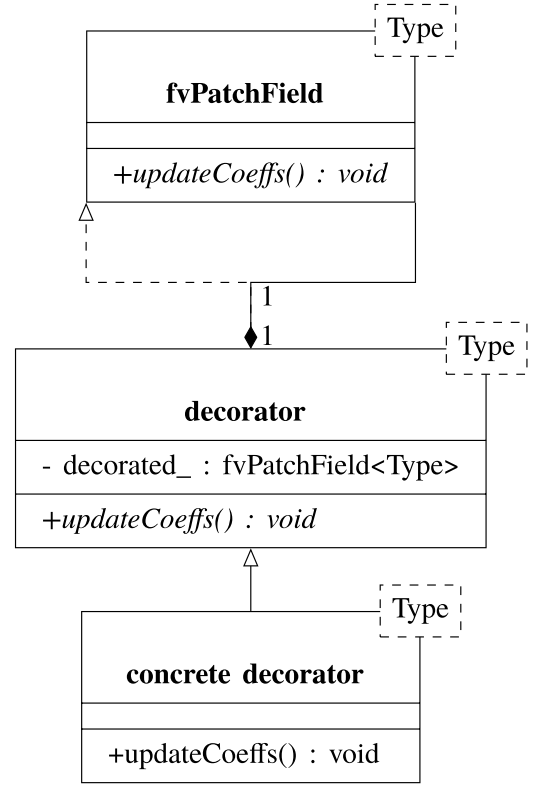
装饰器必须实现抽象类FvPatchField规定的所有纯虚方法。 由于它也合成了一个普通的边界条件,装饰器将根据程序员规定的条件将函数调用委托给装饰的边界条件。 decorator提供的扩展可以根据程序员的需要进行设计。 如图10.5所示,通过结合继承和组合,修饰的边界条件可以在运行时切换自己的类型,因为它将计算委托给修饰器。
10.3.1.2 在边界条件中加入再循环控制
作为在OpenFOAM中为任何边界条件添加运行时功能的一个例子,我们选择流动再循环作为控制参数,来流速度作为边界条件的施加作用。 流动再循环由边界处的体积流量交替符号来识别。 区域边界上体积通量中的交替符号表示涡旋(涡)越过边界。 因此,流体通过边界的一部分流入区域,并通过边界的另一部分流出区域。
在算例模拟中,边界条件检查扩展边界的流动是否存在回流,并试图控制修饰边界条件以减少回流。 这种类型的边界条件修饰器最有可能被设置为一些预期流出的边界条件。 本例中的控件是以一种相当简单的方式完成的:通过修改修饰的边界条件,使其场被增加的流入值覆盖。
当然,这个示例是特定于流入/流出情况的,但是这个示例的目标不是处理流控制。 再循环控制边界条件修饰器不同于OpenFOAM标准边界条件 它直接修改由另一个边界条件计算的场值,而不考虑被修饰的边界条件的类型。 示例代码存储库中已经提供了完成的再循环控制边界条件。 为了便于理解所给出的示例,在描述之后应该使用在文本编辑器中打开的示例代码库中的再循环控制边界条件的代码。 在下面的讨论中,文件和类的名称与示例代码存储库中的名称相同。
注:边界条件必须编译为共享库。 它们永远不应该直接实现到应用程序代码中,因为这极大地限制了它们的可用性以及与其他OpenFOAM程序员的共享。
边界条件编译成的库在运行时与求解器应用程序动态链接。 在本教程开始时,需要创建库目录:
?> mkdir -p primerBoundaryConditions/recirculationControl
?> cd !$
并且需要复制一个现有边界条件的类文件,我们将其用作再循环控制边界条件的骨架文件:
?> cp \
$FOAM_SRC/finiteVolume/fields/fvPatchFields/basic/zeroGradient/* .
字符串“Zerogradient”的所有实例都将在文件名和类名中重命名为“RecirculationControl”。 修改名称后,退出RecirculationControl目录,并创建编译配置文件夹make:
?> cd ..
?> $FOAM_SRC/../wmake/scripts/wmakeFilesAndOptions
并修改make/files以考虑到要编译的是一个库,而不是一个应用程序,因此行
EXE = $(FOAM_APPBIN)/primerBoundaryConditions
需要修改为:
LIB = $(FOAM_USER_LIBBIN)/libofPrimerBoundaryConditions
请注意,脚本wmakeFilesAndOptions将把所有*.C文件插入make/files文件中,这意味着行:
recirculationControl/recirculationControlFvPatchField.C
必须在编译前移除,因为它限制了循环控制边界条件的类模板定义。 这将在编译期间导致类重新定义错误,因为实际的边界条件类是使用宏从张量属性的循环控制类模板中实例化的。
makePatchFields(recirculationControl);
一旦从make/files中删除了文件recirculationControlFvPatchField.C,库就可以进行第一次编译测试了。 编译可以通过命令
?> wmake
从primerBoundaryConditions目录中。 清单49与清单50分别为make/files及make/options文件的最终版本。
# Make/files文件内容
recirculationControl/recirculationControlFvPatchFields.C
LIB = $(FOAM_USER_LIBBIN)/libofPrimerBoundaryConditions
# Make/options文件内容
EXE_INC = \
-I$(LIB_SRC)/finiteVolume/lnInclude \
-I$(LIB_SRC)/meshTools/lnInclude
EXE_LIBS = \
-lfiniteVolume \
-lmeshTools
编译成功后,创建了一个自包含的共享边界条件库的框架实现。 在Decorator功能的进一步开发开始之前,要用实际的模拟运行来测试边界条件。 在这一点上,边界条件与它所基于的zeroGradientFvPatchField具有相同的功能,但名称不同。 它的功能可以通过运行任何模拟案例来测试,只要您在system/controlDict文件中定义所需的链接库:
libs ("libofPrimerBoundaryConditions.so")
这将加载边界条件共享库,并将其链接到OpenFOAM可执行文件。
注:在编写自定义库的过程中,强烈建议执行此类集成测试。使用版本控制系统(第6章)也可以改进工作流。例如,尝试使用icoFoam求解器将再循环控制边界条件应用于空腔教程案例中速度场的fixedWalls边界。
此时,库与OpenFOAM的集成已经过测试,并被认为是有效的。图10.5所示的设计的实施可以开始了。实现Decorator模式的严格的面向对象方法是从fvPatchField的抽象Decorator类开始。在这种情况下,recirculationControl必须作为具体的装饰器模型从它派生出来。相反,在这个例子中使用了一个具体的装饰器作为起点,抽象的实现留给读者作为本节末尾的练习。通过实施该练习,可以在OpenFOAM中为任何边界条件添加不同的功能,而无需修改它们的实现。除了增进对OpenFOAM中边界条件的了解之外,这是进行练习的另一个好处。
对再循环控制边界条件的第一个修改应用于类模板声明文件recirculationControlFvPatchField. H。它继承自fvPatchField,fvPatchField已经由zeroGradientFvPatchField完成。recirculationControlFvPatchField类定义的重要部分显示在代码清单中。
在清单51中,可以看到装饰器模式:存在从fvPatchField的继承,但fvPatchField的私有属性也由再循环控制边界条件类合成。在baseTypeTmp_中实例化本地副本是使用OpenFOAM的智能指针对象tmp完成的,因为它提供了额外的功能,如垃圾收集。这种智能指针依赖于RAII C++习惯用法,极大地简化了指针的处理。声明为常量的其余类属性将从边界条件的字典中读取。
// 程序清单51
template<class Type>
class recirculationControlFvPatchField
:
public fvPatchField<Type>
{
protected:
// Base boundary condition.
tmp<fvPatchField<Type> > baseTypeTmp_;
const word applyControl_;
const word baseTypeName_;
const word fluxFieldName_;
const word controlledPatchName_;
const Type maxValue_;
scalar recirculationRate_;
为了实例化应修饰的边界条件,必须通过边界条件的字典传递特定名称,并将其存储在baseTypeName_ attribute中。为了提供应用或不应用再循环控制的选项,实现了开关applyControl_。如果它为false,则不会在边界上施加任何内容,因此关闭它并简单地使用修饰的边界条件是很容易的。此外,它还将报告扩展边界条件下的再循环量。延伸边界条件的类型由baseTypeName_变数决定,然后使用该变数根据类别名称建立具体的延伸边界条件。此边界条件存储在baseTypeTmp_中。
为了计算再循环,边界条件需要知道体积通量场的名称,该名称是fluxFieldName_属性定义的。受控修补程序字段的名称由controlledPatchName_定义。它可能采用的最大值由成员maxValue_定义,recirculationRate_存储扩展边界条件上负体积通量的百分比。
方法是扩展和修改构造函数初始化列表,以考虑新的私有类属性。为了保持描述简洁,以下文本中仅显示字典构造函数。源代码库中提供了完整的实现。
再循环控制边界条件的构造函数如清单52所示。在初始化列表中,baseTypeTmp_未被赋值,因此取任意值。在建构函式本身中,会使用New选取器建立fvPatchField并指派给baseTypeTmp_。这种构造对象的方式称为工厂方法(新选择器),并在抽象fvPatchField类中定义。它在运行时根据字典中提供的名称选择recirculationControlFvPatchField的基类,构造函数使用字典来初始化修饰边界条件。在执行此构造函数后,将初始化控制函数所需的受保护属性以及修饰边界条件。
template<class Type>
Foam::recirculationControlFvPatchField<Type> ::
recirculationControlFvPatchField
(
const recirculationControlFvPatchField<Type> & ptf,
const fvPatch& p,
const DimensionedField<Type, volMesh> & iF,
const fvPatchFieldMapper& mapper
)
:
fvPatchField<Type> (ptf, p, iF, mapper),
baseTypeTmp_(),
applyControl_(ptf.applyControl_),
baseTypeName_(ptf.baseTypeName_),
fluxFieldName_(ptf.fluxFieldName_),
controlledPatchName_(ptf.controlledPatchName_),
maxValue_(ptf.maxValue_),
recirculationRate_(ptf.recirculationRate_)
{
// Instantiate the baseType based on the dictionary entries.
baseTypeTmp_ = fvPatchField<Type> ::New
(
ptf.baseTypeTmp_,
p,
iF,
mapper
);
}
recirculationControlFvPatchField的其余构造函数必须以类似方式进行修改,以说明新的类属性。一旦修改了构造函数,图10.5中列出的成员函数也需要修改。它们需要将工作委托给存储在baseTypeTmp_中的修饰边界条件。所有四个成员函数的实现都是相同的,所以清单53中只给出了其中一个。
// 程序清单53
template<class Type>
Foam::tmp<Foam::Field<Type> >
Foam::recirculationControlFvPatchField<Type> ::valueInternalCoeffs
(
const Foam::tmp<Foam::Field<scalar> > & f
) const
{
return baseTypeTmp_-> valueInternalCoeffs(f);
}
这种委托需要出现在装饰器实现的所有部分中,在这些部分中不执行流的控制。在这种情况下,边界条件应作为装饰边界条件。图10.5中的具体边界条件模型对此进行了说明。
作为实现再循环控制边界条件的最后一步,需要实现负责边界条件运算的成员函数(updateCoeffs)。实现分为两个主要部分。第一部分检查边界条件是否已更新,这是OpenFOAM边界条件中的常见做法。如果不是这样,则使用通量场fluxFieldName_的用户定义名称查找通量场。
正、负体积通量由扩展边界条件计算,如清单54所示。一旦计算出正和负体积流量,再循环率(负流量与总流量之比)将使用清单55中所示的代码进行计算。
// 程序清单54
if (this-> updated())
{
return;
}
typedef GeometricField <Type, fvPatchField, volMesh> VolumetricField;
// Get the flux field
const Field<scalar> & phip =
this-> patch().template lookupPatchField
<
surfaceScalarField,
scalar
> (fluxFieldName_);
// Compute the total and the negative volumetric flux.
scalar totalFlux = 0;
scalar negativeFlux = 0;
forAll (phip, I)
{
totalFlux += mag(phip[I]);
if (phip[I] < 0)
{
negativeFlux += mag(phip[I]);
}
}
// 程序清单55
// Compute recirculation rate.
scalar newRecirculationRate = min
(
1,
negativeFlux / (totalFlux + SMALL)
);
Info << "Total flux " << totalFlux << endl;
Info << "Recirculation flux " << negativeFlux << endl;
Info << "Recirculation ratio " << newRecirculationRate << endl;
// If there is no recirculation.
if (negativeFlux < SMALL)
{
// Update the decorated boundary condition.
baseTypeTmp_-> updateCoeffs();
// Mark the BC updated.
fvPatchField<Type> ::updateCoeffs();
return;
}
在不发生再循环的条件下,再循环控制和装饰边界条件的行为相同。因此,场的修改被委托给封装的混凝土边界条件模型。注意,因为边界条件装饰器本身是边界条件,所以每次发生更新时,边界条件状态必须被设置为最新。通常,必须为此调用fvPatchField抽象类的成员函数updateCoeffs。updateCoeffs成员函数中负责控制再循环的部分如清单56所示。
// 程序清单56
if (
(applyControl_ == "yes") &&
(newRecirculationRate > recirculationRate_)
)
{
Info << "Executing control..." << endl;
// Get the name of the internal field.
const word volFieldName = this-> internalField().name();
// Get access to the regitstry.
const objectRegistry& db = this-> db();
// Find the GeometricField in the registry using
// the internal field name.
const VolumetricField& vfConst =
db.lookupObject<VolumetricField> (volFieldName);
// Cast away constness to be able to control
// other boundary patch fields.
VolumetricField& vf = const_cast<VolumetricField&> (vfConst);
// Get the non-const reference to the boundary
// field of the GeometricField.
typename VolumetricField::Boundary& bf =
vf.boundaryFieldRef();
// Find the controlled boundary patch field using
// the name defined by the user.
forAll (bf, patchI)
{
// Control the boundary patch field using the recirculation rate.
const fvPatch& p = bf[patchI].patch();
if (p.name() == controlledPatchName_)
{
if (! bf[patchI].updated())
{
// Envoke a standard update first to avoid the field
// being later overwritten.
bf[patchI].updateCoeffs();
}
// Compute new boundary field values.
Field<Type> newValues (bf[patchI]);
scalar maxNewValue = mag(max(newValues));
if (maxNewValue < SMALL)
{
bf[patchI] == 0.1 * maxValue_;
} else if (maxNewValue < mag(maxValue_))
{
// Impose control on the controlled inlet patch field.
bf[patchI] == newValues * 1.01;
}
}
}
}
该边界条件将需要对另一边界条件的场进行非常量的访问,因为它将修改边界场值。因此,它通过强制丢弃注册表提供的VolumetricField的常量来破坏objectRegistry类的封装。清单57显示了对另一个边界字段的非常量访问。
//程序清单57
// Cast away constness to be able to control other boundary patch fields.
VolumetricField& vf = const_cast<VolumetricField&> (vfConst);
// Get the non-const reference to the boundary field of the GeometricField.
typename VolumetricField::GeometricBoundaryField& bf = vf.boundaryField();
注:在任何可能的情况下,都应该避免以这种方式抛弃constness:它使封装点无效--只能由类成员函数修改的对象状态。此示例使用常量转换仅指向几何字段和对象注册表之间可能的协作。
如果objectRegistry的接口只提供对已注册对象的常量访问,那么抛弃常量并修改对象状态就是在欺骗程序员。他/她将不期望经由objectRegistry的接口能够改变VolumetricField对象状态。算法1阐明了伪代码中的再循环控制算法。
该边界条件主要是作为将装饰器模式应用于OpenFOAM中的边界条件类层次结构的示例。然而,这里应用的设计可以很好地用于存在入口/出口边界条件的情况。在某些情况下,可以通过增加例如入口压力或速度来实现再循环的减少。不过,请注意,这只是说明两个主要问题的示例:首先,它显示了如何使用VolumetricField的设计来耦合不同边界条件之间的功能。其次,说明了如何在OpenFOAM中编程一个新的边界条件,该边界条件是从fvPatchField导出的。
10.3.1.3 测试再循环控制边界条件
实现updateCoeffs方法后,即可使用边界条件。作为一个测试用例,使用了一个带有后向台阶的简单后向通道。在通道出口采用回流控制,控制边界条件为后向台阶壁。
图10.6描述了流动的初始形态,其中向后台阶的速度设置为零,因为它是一个不可渗透的壁面。当出口出现再循环时,再循环控制边界条件将超越后向台阶的零速度。进一步,它将把应用于左壁面边界的边界条件转换为入流,以便将再循环排出。
图10.7给出了有无再循环控制边界条件下速度场的比较。
注:此测试用例的设置可在示例用例库的ofbookcases/chapter 10/recirculationControlChannel文件夹中获得,并使用icoFoam求解器对瞬态层流不可压缩单相流进行模拟。
练习:
此示例中未实现抽象装饰器:修改recirculationControlFvPatchField,以便将抽象装饰器添加到类层次结构中。该装饰器概括了边界条件的装饰,从而能够在运行时向OpenFOAM中的任何边界条件添加任何功能。
10.3.2 网格运动边界条件
本小节说明了用于网格运动的新边界条件的构造。网格的运动依赖于以边界条件的形式为网格的点定义的位移或速度,该边界条件与属于网格边界的边界点相关联,在OpenFOAM中称为pointPatchField。与基于fvPatchField的边界条件不同,pointPatchField类型的边界条件不会将边界值存储在边界字段中,而是用于修改内部字段的值。更改内部字段值和任何其他操作由求解器或使用这些边界条件的其他类处理。网格运动边界条件所使用的矢量量将定义特定网格点的速度或位移,这取决于网格运动求解器的选择。
在本节中,网格运动解算器将使用dynamicFvMesh库,在模拟示例中,它将使用新边界条件定义的边界处的位移解算点位移的拉普拉斯方程。由于拉普拉斯方程用于模拟扩散输运,在网格边界处规定的位移将平滑地扩散到周围的网格,这确保了变形单元的更高质量。对于此类应用程序,存储点变形的字段称为pointDisplacement。
本节中介绍的边界条件从输入文件中读取面片重心的位置和方向,并将位移应用于网格边界(相对于其先前位置),并且必须与动态网格结合使用,否则将无法读取pointDisplacement字段。边界条件功能由OpenFOAM的两个现有组件组成:
- 计算面片重心(COG)的位置,该位置是基于字典中包含的指定运动计算的。这种规定的运动必须以表格的形式出现,并在每个数据点之间进行线性插值。所有这些都已在tabulated6DoFMotion中实现,它是一个dynamicFvMesh类,可根据指定的运动移动整个网格。
- 将向量值赋给pointPatchField。 这类边界条件的一个例子是oscillatingDisplacementPointPatchVectorField
对于从fvPatchField导出的边界条件,仅更改域边界上的值。任何边界条件都不会对模拟或现场进行额外更改,并且功能以逻辑方式封装。对于fvPatchField边界条件,流求解器使用边界值计算场变量。相同的原则适用于从pointPatchField导出的边界条件。边界条件仅规定速度或位移,而实际网格更改由专用网格运动解算器(dynamicFvMesh库的一部分)执行。在下文中,将简要介绍这两个组件,并突出显示与新边界条件相关的部分。
10.3.2.1 读取运动数据
在OpenFOAM的现有代码库中进行简单搜索,发现有一个网格运动解算器,它从表格文件中读取运动数据,与此边界条件的计划类似。但是,在这种情况下,会将相同的位移套用至所有网网格节点,从而产生将网面做为刚体移动的网面运动:不会发生网格变形,网格点的相对位置不会改变。出于本教程的目的,可以使用运动计算,然后将其应用于面片点,使网格边界作为刚体移动。当物体相对于网格(流域)的相对运动小时,这种网格运动可能是有益的。在这种情况下,如果运动以类似扩散的方式传播到流域中,则远离具有规定位移的边界的网格的运动将接近于零。位移从物体消失的速度由位移扩散系数的大小决定。
基于表格数据实现刚体网格运动的代码包含在tabulated6DoFMotionFvMesh类中,该类派生自solidBodyMotionFunction,可在以下位置找到:
$FOAM_SRC/dynamicMesh/motionSolvers/displacement/solidBody/\
solidBodyMotionFunctions/tabulated6DoFMotion/
在正式版本中有一个示例案例,它使用tabulated6DoFMotion来规定封闭罐的运动。本教程可在此处找到:
$FOAM_TUTORIALS/multiphase/interFoam/laminar/sloshingTank3D6DoF
包含运动数据(时间点)的字典被建立为列表(使用列表数据结构),该列表由时间t中的平移和旋转向量组成。此数据的示例可在上述教程中的constant/6DoF.dat中找到。下面的代码片段说明了字典建立的原理。
(
(t1 ((Translation_Vector_1) (Rot_Vector_1))
(t2 ((Translation_Vector_2) (Rot_Vector_2))
...
)
执行基于样条的插值以获得字典的数据点之间的位置和取向数据。平移和旋转向量是相对于原始坐标系定义的,如图10.8所示。
由于第13章仅涉及动态网格,因此为了更清楚起见,仅提供了solidBodyMotionFvMesh类型的动态网格的工作原理的简要总结:
- 从solidBodyMotionFvMesh派生的动态网格仅处理实体的运动
- 不能执行拓扑更改,实体面片也不能更改其形状
- 运动本身不是由solidBodyMotionFvMesh定义的,这是solidBodyMotionFunction和派生类的作用
- 这简化了运动计算与实际网格运动算法的分离
- tabulatedSixDoF类继承自solidBodyMotionFunction,后者是OpenFOAM中所有实体运动函数的基类。
如果在dynamicMeshDict中选择了类型为solidBodyMotionFvMesh的动态网格,则在使用运行时选择构建dynamicFvMesh期间将实例化solidBodyMotionFvMesh。从常量/dynamicMeshDict的子字典中读取特定参数,常量/dynamicMeshDict是称为SBMFCoeffs_的私有类属性。下文描述了该边界条件的程序代码的相关部分。
清单58显示了从输入字典中阅读列表数据。数据和文件名从dynamicMeshDict的子字典读入类型为Tuple2的列表。Tuple2类是一种数据结构,它存储两个可以是不同类型的对象。在上面的示例中,标量与translationRotationVectors的实例存储在Tuple2中,第一个实例是时间,第二个实例是嵌套向量,一个用于平移,一个用于旋转。因此,运动文件的内容直接存储在该数据结构中。为了提供对该数据的轻松访问,创建了单独的列表,如上面代码片段的后半部分所示。
fileName newTimeDataFileName
(
fileName(SBMFCoeffs_.lookup("timeDataFileName")).expand()
);
IFstream dataStream(timeDataFileName_);
List<Tuple2<scalar, translationRotationVectors> > timeValues
(
dataStream
);
times_.setSize(timeValues.size());
values_.setSize(timeValues.size());
forAll(timeValues, i)
{
times_[i] = timeValues[i].first();
values_[i] = timeValues[i].second();
}
从输入数据计算转换是由公共成员函数transformation()执行的,相关内容如清单59所示。第二分配内插当前时间t的位置和取向数据。所有角度都必须转换成弧度,最后用quaternions和septernions.组合了变换的表示。
scalar t = time_.value();
// -- Some lines were spared --
translationRotationVectors TRV = interpolateSplineXY
(
t,
times_,
values_
);
// Convert the rotational motion from deg to rad
TRV[1] *= pi/180.0;
quaternion R(TRV[1].x(), TRV[1].y(), TRV[1].z());
septernion TR(septernion(CofG_ + TRV[0])*R*septernion(-CofG_));
构造对象当然是通过构造函数来完成的,构造函数有两个参数,如下面的清单所示。第一个是对包含tabulated6DoFMotion所需数据的字典的引用,它是数据文件的路径。将引用传递给“时间”可简化数据点之间的插值:
tabulated6DoFMotion
(
const dictionary& SBMFCoeffs,
const Time& runTime
);
找到负责点运动的代码后,下一步是找到从pointPatchField派生的边界条件,该边界条件执行与我们计划实现的任务类似的任务:由此我们计划建立我们自己边界条件。
10.3.2.2 调整现有边界条件
现有的oscillatingDisplacementPointPatchVectorField边界条件是导出网格运动边界条件的良好起点。它根据时间相关正弦曲线将位移值应用于存储在边界上的点中的每个值。可以在fvMotionSolver的子目录中找到oscillatingDisplacementPointPatchVectorField的源代码:
?> $FOAM_SRC/fvMotionSolver/pointPatchFields/derived/oscillatingDisplacement/
如本章开头关于fvPatchField类型边界条件的讨论,边界条件的实际功能在evaluate()或updateCoeffs()成员函数中实现。在oscillatingDisplacementPointPatchVectorField边界条件的情况下,成员函数updateCoeffs()计算边界网格的每个点的位移向量。位移向量定义如下:
amplitude_*sin(omega_*t.value())
其中amplitude_和omega_都是从字典中读取的标量值(omega是角旋转)。这个方法的实现可以如清单60中所示。
//程序清单60
void oscillatingDisplacementPointPatchVectorField::updateCoeffs()
{
if (this-> updated())
{
const polyMesh& mesh =
this-> dimensionedInternalField().mesh()();
const Time& t = mesh.time();
Field<vector> ::operator=(amplitude_*sin(omega_*t.value()));
fixedValuePointPatchField<vector> ::updateCoeffs();
}
fixedValuePointPatchField<vector> ::updateCoeffs();
}
updateCoeffs()方法中Field<vector> ::operator=(amplitude_*sin(omega_*t.value()));的使用Field的指定运算符将适当的置换值指定给网格的边界点。此指令之后是对父类的updateCoeffs()的调用。通过将面片的置换指定给面片点,动态网格解算器可以处理实际的网格运动。
10.3.2.3 组合边界条件
这个边界条件的工作版本可以在随书分发的示例代码存储库中找到,该存储库与前一章的再循环控制边界条件一起捆绑到库primerBoundaryConditions.中。 为了更容易地隐藏,您可能希望在文本编辑器中打开即用网格运动边界条件的源代码,同时遵循此处描述的步骤。 与其他编程示例类似,本示例的边界概念应该使用wmake libso编译到动态库中。 像往常一样,第一步是创建一个新目录来存储边界条件:
?> mkdir -p $WM_PROJECT_USER_DIR/applications/tabulatedRigidBodyDisplacement
?> cd $WM_PROJECT_USER_DIR/applications/tabulatedRigidBodyDisplacement
下一步是将oscillatingDisplacementPointPatchVectorField复制到新目录:
?> cp $FOAM_SRC/fvMotionSolver/pointPatchFields/derived/oscillatingDisplacement/* .
若要保持tabulatedRigidBodyDisplacement边界条件的名称正确,所有出现的oscillatingDisplacement都必须由tabulatedRigidBodyDisplacement取代。这既适用于文件名,也适用于源文件本身内部的匹配。删除 *.dep文件后,必须相应地重命名剩余的C和H文件。
?> rm *.dep
?> mv oscillatingDisplacementPointPatchVectorField.H tabulatedRigidBodyDisplacement.H
?> mv oscillatingDisplacementPointPatchVectorField.C tabulatedRigidBodyDisplacement.C
?> sed -i "s/oscillating/tabulatedRigidBody/g" *.[HC]
首先要检查的是重命名的oscillatingDisplacementPointPatchVectorField是否仍能正确编译。要检查这一点,需要创建OpenFOAM典型的Make/文件和Make/选项文件:
?> mkdir Make
?> touch Make/files
?> touch Make/options
文件的内容很短,因为边界条件仅包含一个源文件:
tabulatedRigidBodyDisplacementPointPatchVectorField.C
LIB = $(FOAM_USER_LIBBIN)/libtabulatedRigidBodyDisplacement
为简单起见,代码库中提供的所有示例边界条件都被编译到一个库中。此库的名称与上述代码段中定义的名称不同。
不过,这个源文件有很多依赖项。其他各种库及其头文件必须链接到此库:
EXE_INC = \
-I$(LIB_SRC)/finiteVolume/lnInclude \
-I$(LIB_SRC)/dynamicFvMesh/lnInclude \
-I$(LIB_SRC)/meshTools/lnInclude \
-I$(LIB_SRC)/fileFormats/lnInclude
LIB_LIBS = \
-lfiniteVolume \
-lmeshTools \
-lfileFormats
通过在包含Make文件夹的目录中发出wmake libso命令,测试边界条件是否仍能编译。如果编译时没有出现任何错误和警告,请在您选择的编辑器中打开头文件和源文件,并应用以下更改。首先,头文件必须包含在tabulatedRigidBodyDisplacementPointPatchVectorField.H中:
#include "fixedValuePointPatchField.H"
#include "solidBodyMotionFunction.H"
源文件必须包含更多的头文件:
#include "tabulatedRigidBodyDisplacementPointPatchVectorField.H"
#include "pointPatchFields.H"
#include "addToRunTimeSelectionTable.H"
#include "Time.H"
#include "fvMesh.H"
#include "IFstream.H"
#include "transformField.H"
所需功能的实际实现是在updatecoeffs()成员函数中完成的。 尽管这里使用了一个私有属性,但它没有实现:一个constant字典,它包含在0/目录中边界条件字典中定义的所有数据。 这个字典被添加到头文件中的私有属性中:
//- Store the contents of the boundary condition's dicitonary
const dictionary dict_;
边界条件的每个构造函数都必须初始化新的私有属性,这通常是通过调用dicitonary的null-constructor来完成的。 一个例子是从PointPatch和DimensionedField构造边界条件的构造函数,如清单61所示。 如果边界条件是通过从0目录读取特定文件来构造的,则调用以下构造函数。 事实上,边界条件的字典被传递给构造函数,并且必须存储在边界条件中以便以后处理:
// 清单61
tabulatedRigidBodyDisplacementPointPatchVectorField::
tabulatedRigidBodyDisplacementPointPatchVectorField
(
const pointPatch& p,
const DimensionedField<vector, pointMesh> & iF
)
:
fixedValuePointPatchField<vector> (p, iF),
dict_()
{}
tabulatedRigidBodyDisplacementPointPatchVectorField::
tabulatedRigidBodyDisplacementPointPatchVectorField
(
const pointPatch& p,
const DimensionedField<vector, pointMesh> & iF,
const dictionary& dict
)
:
fixedValuePointPatchField<vector> (p, iF, dict),
dict_(dict)
{
updateCoeffs();
}
此构造函数是唯一在构造期间调用updateCoeffs()的构造函数。updateCoeffs成员函数如清单62所示。最重要的行是定义SBMFPtr的行。它基于字典和Time对象为solidBodyMotionFunction构造autoPtr。由于此代码源自dynamicFvMesh库,因此传递给构造函数的字典是dynamicMeshDict的子字典。此子字典包含用户在dynamicMeshDict中选择的solidBodyMotionFunction所需的所有参数。由于此边界条件的运动参数定义应基于每个边界而非全局执行,因此传递给构造函数的字典应从0目录中的边界条件读取,而不是从dynamicMeshDict读取。这就是私有成员dict_的作用:它只读取一次,并在每次调用updateCoeffs()时传递给solidBodyMotionFunction。
// 清单62
void tabulatedRigidBodyDisplacementPointPatchVectorField::updateCoeffs()
{
if (this-> updated())
{
return;
}
const polyMesh& mesh = this-> dimensionedInternalField().mesh()();
const Time& t = mesh.time();
const pointPatch& ptPatch = this-> patch();
autoPtr<solidBodyMotionFunction> SBMFPtr
(
solidBodyMotionFunction::New(dict_, t)
);
pointField vectorIO(mesh.points().size(),vector::zero);
vectorIO = transform
(
SBMFPtr().transformation(),
ptPatch.localPoints()
);
Field<vector> ::operator=
(
vectorIO-ptPatch.localPoints()
);
fixedValuePointPatchField<vector> ::updateCoeffs();
}
下一行与tabulated6DofMotion中的行类似。 应用转换后的补丁点的绝对位置存储在vectorIO.中。 由于实际运动相对于先前的点位置,必须计算差值,这是直接在调用赋值算子中完成的。转换是使用间septernions进行的,在许多方面优于转换矩阵。
既然源代码已经准备好了,请再次编译库。
?> wclean
?> wmake libso
10.3.2.4 在示例案例中执行模拟
首先,应使用示例代码库中准备好并经过测试的代码执行示例案例中的模拟。一旦运行了分布式代码,字典中的必要输入参数以及应用于字段的修改应该是清楚的,并且可以测试所实现的边界条件。范例案例tabulatedMotionObject位于范例案例储存库中。该三维情况是新实现的平板刚体运动边界条件的功能的简单演示。图10.9显示了案例设置的示意图,包括一个立方体域和一个从中间切除的体积。由该切割过程创建的边界由movingObject面片表示。
movingObject将根据6DoF.dat文件中常量/中包含的数据由新的边界条件进行位移。与基本的OpenFOAM情况相比,执行新的边界条件需要新的配置文件:0/pointDisplacement和常量/dynamicMeshDict文件。使用新的边界条件为pointDisplacement字段的movingObject面片设置初始边界值,如清单63所示。为了使用边界条件,需要将在运行时动态加载新库的指令添加到system/controlDict配置文件中。请注意,如果使用本节中提供的代码编译边界条件,则库的名称会有所不同(“libofPrimerBoundaryConditions.so“)。
//清单63
movingObject
{
type tabulatedRigidBodyDisplacement;
value uniform (0 0 0);
solidBodyMotionFunction tabulated6DoFMotion;
tabulated6DoFMotionCoeffs
{
CofG ( 0 0 0 );
timeDataFileName "constant/6DoF.dat";
}
}
需要dynamicMeshDict来控制网格运动解算器。在这种情况下,使用了displacementLaplacian smoother,它基于拉普拉斯方程并平滑点位移。如果周围的点不随膜片移动,近端网格将迅速变形和破碎。清单64显示了dynamicMeshDict的内容。
// 清单64
dynamicFvMesh dynamicMotionSolverFvMesh;
motionSolverLibs ("libfvMotionSolvers.so");
solver
displacementLaplacian;
displacementLaplacianCoeffs
{
diffusivity
inverseDistance (floatingObject);
}
}
可以通过在Simulation case目录中执行allrun脚本来运行模拟。 此脚本执行所有必要的步骤,如网格生成,以轻松完成此示例。 求解器MovedynamicMesh工具只调用动态网格例程,没有任何与流相关的计算,这使得它相对于具有动态网格功能的通常流求解器来说相对较快。 除了执行网格运动操作,它还执行大量与网格相关的质量检查。
案例的后处理非常简单,可通过目视进行:可以在Paraview中检查该案例。为案例设置动画时,会显示内部面片在域内翻滚和摇摆,类似于输入文件中提供的数据。使用带有“Crickle Clip2”选项的“Clip”过滤器将域切成两半,可以阐明与动态网格有关的一些有趣的事情:由边界条件施加的点位移由网格运动求解器耗散的方式。拉普拉斯方程将位移耗散到内部网格点,相应地移动这些点,并在面片平移和旋转时保持良好的网格质量。图10.10显示了变换前后最终面片位置的图像。

总结
本章介绍了OpenFOAM中FV法和网格运动边界条件的设计与实现。 这两个边界条件族分别被建模为两个分离的类层次结构,FVPatchField和PointPatchField。 动态多态性允许现有实现的不同扩展和组合。 将边界条件与存储在内部网格点中的物理场一起实现为类层次结构,允许OpenFOAM库在运行时确定边界条件的类型,而无需在每次为场设置新的边界条件时重新编译代码。 动态库的加载机制允许将边界条件的新实现编译到单独的库中(例如FinitEvolume库)。 这反过来又产生了一种直接添加新边界条件的方法,而不必重新编译数值库。 这些优点允许程序员通过开发(和共享)自我维持的库来扩展边界条件和OpenFOAM的其他部分。
开发新的边界条件涉及到在类层次结构中找到一个入口点,从这个入口可以扩展层次结构。 选择类作为边界条件进一步发展的起点取决于所需边界条件实现的功能,以及是否已经存在类似的边界条件。 计算部分边界条件位于Updatecoeffs成员函数中。 除了适当地重命名源文件和修改新类以进行继承之外,程序员很可能会完成大部分工作来实现这个函数的主体。
- Erich Gamma et al. Design patterns: elements of reusable object-oriented software. Addison-Wesley Longman Publishing Co., Inc., isbn: 0-201-63361-2.
- OpenFOAM User Guide. OpenCFD limited. 2016.
本章介绍了粘度模型在 Open- FOAM 中的实现,OpenFOAM 中的其他传输模型也有类似的结构,可以根据本章介绍的信息进一步开发。
本章介绍了OpenFOAM中粘度模型的实现,OpenFOAM中的其他传输模型具有类似的结构,可以根据本章中提供的信息进一步开发。
OpenFOAM中提供了各种流体的粘度模型,因此本节将简要介绍粘度模型的物理和数值方面。粘度模型的实现在第11.2节中进行了介绍。有关粘度的更多信息,请参见[3,4]和类似的流体动力学教科书。
通常用于描述流体粘度的流动结构是所谓的库埃特流:两个平行板之间的流动以距离分开。下平面在空间中固定不动,而上平面以恒定速度运动。如图11.1所示。
随着时间的推移,两个板块之间的速度梯度逐渐增大,从而产生应力,该应力作用于[3]中的上板块,即 其中表示以下列方式与运动粘度相关的动力粘度: 运动粘度是OpenFOAM用户指定的流体特性。大多数流体可以是牛顿流体:在牛顿流体中,粘性应力与应变率(速度梯度)线性相关。非牛顿流体表现出非线性应力-应变模型。为了便于模拟各种流体,OpenFOAM包括各种粘度模型以及标准牛顿模型: :
- Newtonian表示 为常数的不可压缩牛顿流体
- BirdCarreau表示不可压缩Bird-Carreau非牛顿流体
- CrossPowerLaw表示基于非牛顿流体的不可压缩Cross-Power定律
- Casson表示Casson非牛顿流体
- HerschelBulkley表示Herschel-Bulkley非牛顿流体
- PowerLaw表示基于幂律的非牛顿流体
- Arrhenius其中粘度是一些其他标量(通常是温度)的函数。
粘度模型并不是影响粘度的唯一模型:湍流模型改变了所谓的有效粘度(参见第7章)。 如果湍流模型被禁用,粘度模型只决定了。
OpenFOAM传输模型库由两个主要组件组成:传输模型和粘度模型。粘度模型提供了直接面向对象的访问粘度相关的计算和数据。本节使用主要类的简化UML图来介绍OpenFOAM中粘度模型的类关系,如图11.2所示。
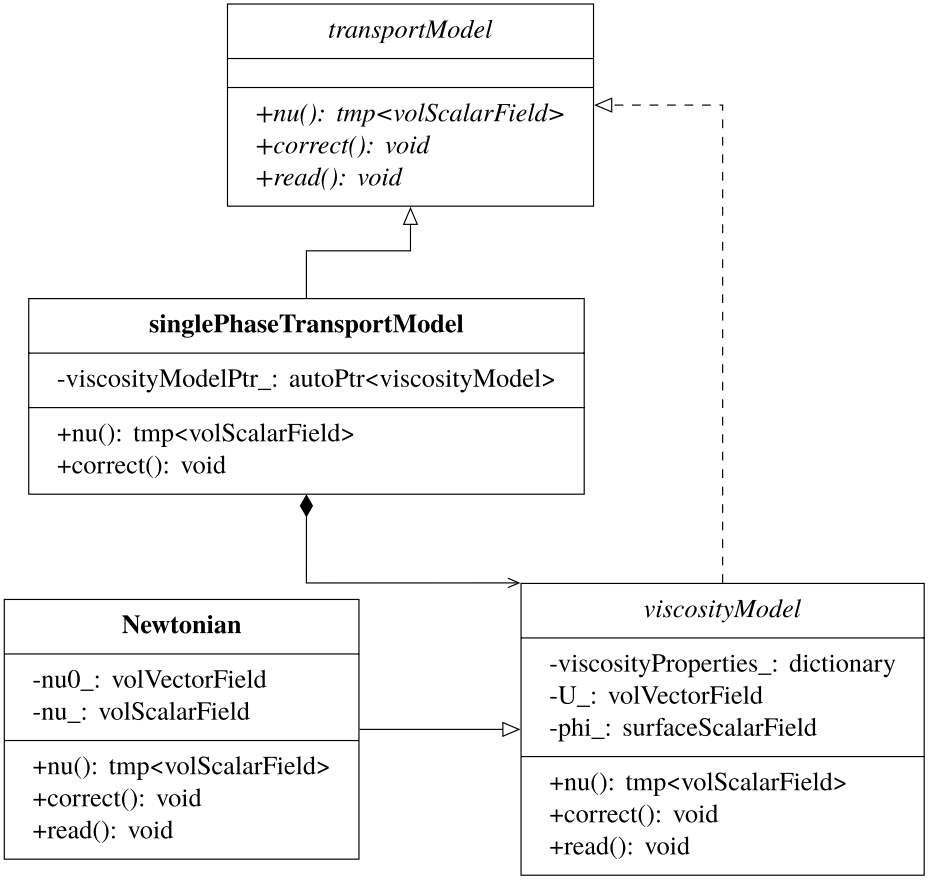
基类为transportModel,它继承自IOobject。transportModel类在构造函数中初始化,以读取相应OpenFOAM案例的cosntant/transportProperties字典。清单65显示了transportModel的构造函数和IOobject的初始化:
Foam::transportModel::transportModel
(
const volVectorField& U,
const surfaceScalarField& phi
)
:
IOdictionary
(
IOobject
(
"transportProperties",
U.time().constant(),
U.db(),
IOobject::MUST_READ_IF_MODIFIED,
IOobject::NO_WRITE
)
)
{}
传输模型的实现将单相流模型与两相流模型分离为transportModel类的两个派生类:singlePhaseTransportModel和incompressibleTwoPhaseMixture。 这种划分是由于单相流和两相流之间的天然差异。
在OpenFOAM,所有的单相求解器都使用singlePhaseTransportModel类来获取和加载运动粘度Nu。 此参数必须由用户在constant/transportProperties字典中提供。 singlePhaseTransportModel和其他传输模型委托读取和更新该字典的过程,这有助于保持代码的干净。 在单阶段求解器中,singlePhaseTransportModel实例化如下:
singlePhaseTransportModel laminarTransport(U, phi);
请注意,湍流模型的构造函数需要laminarTransport对象作为参数,因为湍流模型需要访问层流粘度,而层流粘度又由singlePhaseTransportModel描述。
transportModel和singlePhaseTransportModel都定义了一个公共成员函数nu(),该函数将粘度作为volScalarField返回。因为transportModel是一个抽象基类,它不实现这个成员函数,而singlePhaseTransportModel类必须实现这个成员函数(见图11.2)。然而,它的实现将功能委托给viscosityModel:
Foam::tmp<Foam::volScalarField>
Foam::singlePhaseTransportModel::nu() const
{
return viscosityModelPtr_-> nu();
}
viscosityModelPtr_是singlePhaseTransportModel的私有成员,并且被定义为viscosityModel的autoPtr。此类属性在头文件中定义为:
autoPtr<viscosityModel> viscosityModelPtr_;
现在,唯一重要的是viscosityModel以某种方式确定运动粘度。下面讨论其实际实现以及如何选择viscosityModel。
两相传输模型由不可压缩的TwoPhaseMixture类建模,由OpenFOAM中不涉及相变的interFoam类型解算器使用。与大多数单相解算器类似,interFoam类型解算器以下列方式实例化该类的对象:
incompressibleTwoPhaseMixture twoPhaseProperties(U, phi);
不可压缩两相混合物模型的课堂协作如图11.3所示。该实例化类似于已经用于singlePhaseTransportModel的方法,但是,不可压缩的TwoPhaseMixture类存储附加数据。不是具有一个viscosityModel,而是由该类实例化并存储两个viscosityModel以说明每个流体相。
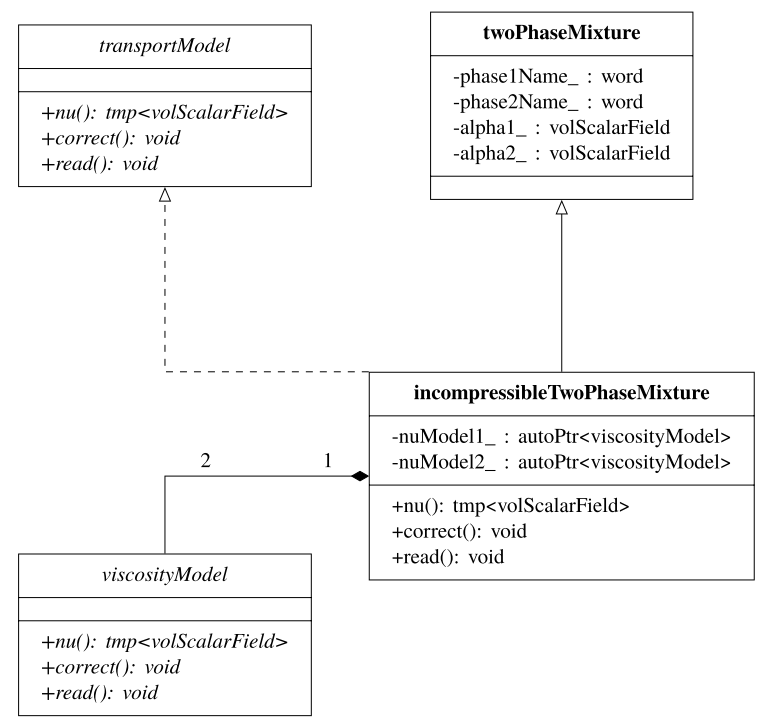
incompressibleTwoPhaseMixture的类定义如清单66所示。使用autoPtr存储viscosityModel的任何派生类的对象是强制性的,因为从viscosityModel派生的不同流体类型有几个不同的类。它们中的每一个都是运行时可选择的,并且最终确定选择哪种流体,这又定义了粘度,并且因此定义了公共成员函数nu的返回值。为了区分两种流体相,引入了新的volScalarField对象alpha1_。
// 清单66
class incompressibleTwoPhaseMixture
:
public transportModel,
public twoPhaseMixture
{
protected:
// Protected data
autoPtr<viscosityModel> nuModel1_;
autoPtr<viscosityModel> nuModel2_;
dimensionedScalar rho1_;
dimensionedScalar rho2_;
const volVectorField& U_;
const surfaceScalarField& phi_;
volScalarField nu_;
该字段用于VoF成员函数,是两相属性(如粘度和密度)之间的有效混合值。与singlePhaseTransportModel不同的是,在singlePhaseTransportModel中,对公共成员函数nu的调用被直接委托给所选择的viscosityModel,该公共成员函数的返回值以不同的方式构成。返回私有成员nu_的副本,其是基于两个相的viscosityModels和当前alpha1_字段计算的。此计算由私有成员calcNu执行,并在调用公共成员函数correct时触发,如清单67所示。
//清单67
void Foam::incompressibleTwoPhaseMixture::calcNu()
{
nuModel1_-> correct();
nuModel2_-> correct();
const volScalarField limitedAlpha1
(
"limitedAlpha1",
min(max(alpha1_, scalar(0)), scalar(1))
);
// Average kinematic viscosity calculated from dynamic viscosity
nu_ = mu()/(limitedAlpha1*rho1_ + (scalar(1) - limitedAlpha1)*rho2_);
}
更新两个viscosityModel,并且将体积分数alpha_1限制在0和1之间。最后,使用动态粘度mu和密度分布计算运动粘度。后者是用混合物在各相密度和体积分数alpha_1的项中的规则计算的。使用有界的alpha1_和每个viscosityModel的运动粘度nu,类似地计算动力粘度mu。
到目前为止,重点放在transportModel及其衍生模型上,而viscosityModel只是简单提及。viscosityModels类负责建模和计算粘度,遵循OOD模式单一责任原则(SRP)。粘度模型列表及其描述见第11.1节。与transportModel的结构类似,viscosityModel类是实际粘度模型的抽象基类。
如图11.2所示,viscosityModel实现了一个公共成员函数nu,它最终返回运动粘度。此成员函数提供对任何transportModel中粘度的访问。在基类viscosityModel中,这是一个虚拟成员函数,需要由每个派生类实现:
virtual tmp<volScalarField> nu() const = 0;
将singlePhaseTransportModel和incompressibleTwoPhaseMixture硬编码到特定解算器中,viscosityModel是用户选择的最终类型。因此,必须使用constant/transportProperties字典中的特定条目在运行时选择它们。因此,基底类别必须实作OpenFOAM RTS机制。
选择Newtonian类作为viscosityModel的示例。它描述不可压缩牛顿流体的粘度,并且仅继承自viscosityModel。其他数据存储在以下私有成员变量中:
dimensionedScalar nu0_;
volScalarField nu_;
nu成员函数必须由该类实现,因为它的基类定义是虚拟的。这个实作是简短的,并传回nu_。构造函数如清单68所示。
Foam::viscosityModels::Newtonian::Newtonian
(
const word& name,
const dictionary& viscosityProperties,
const volVectorField& U,
const surfaceScalarField& phi
)
:
viscosityModel(name, viscosityProperties, U, phi),
nu0_("nu", dimViscosity, viscosityProperties_),
nu_
(
IOobject
(
name,
U_.time().timeName(),
U_.db(),
IOobject::NO_READ,
IOobject::NO_WRITE
),
U_.mesh(),
nu0_
)
{}
当然,基类的构造函数在初始化列表的第一个位置被调用,然后是nu0_和nu的初始化。
注意:即使transportModel是所有运输模型的抽象基类,专业的求解器也会选择层次结构中的其他模型类。一个例子是不可压缩的TwoPhaseMixture,它是一个传输模型,但也是一个twoPhaseMixture,特别是要由两相求解器使用。
自定义viscosityModel的实现是基于粘度取决于剪切速率的示例构建的。
以血液作为流体示例,粘度与剪切速率相关的实验数据见[1,图2]。使用engauge数字化仪将[1]中的实验数据数字化为CSV文件,第一列为应变率,第二列为相应的有效动力粘度。
注:该示例侧重于在OpenFOAM中实现新的粘度模型,而不是模型的物理正确性。
运动粘度通过除以室温下血液的近似密度得到,如图11.4所示。
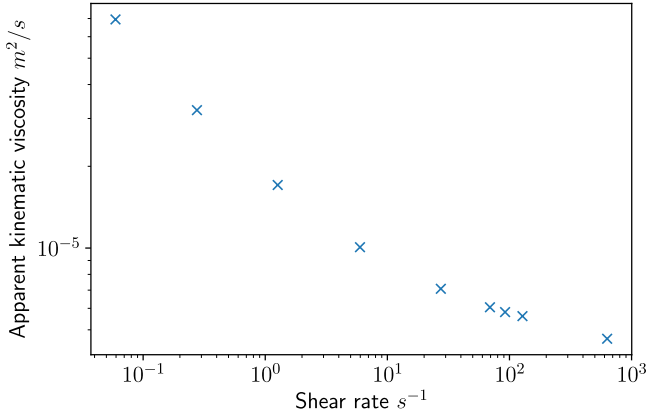
本示例介绍如何实现一个新的粘度模型类,该模型类读取运动粘度和局部应变率,并返回有效粘度。这种基于数据表的方法与其他更常见的粘度模型形成对比,后者使用应变率与粘度关系的解析表达式。图11.4显示了剪切流变仪的一组测量值示例(有效粘度与应变率)。由于流变仪表中只有离散的数据点,因此必须使用插值方案在它们之间进行插值,并将粘度分配给任何给定的应变率。OpenFOAM提供了可用于此目的基于二维样条的插值:插值XY样条线。此库的源代码可在示例存储库中找到,位于:
ofbook/ofprimer/src/ofBookTransportModels
这里,仅涉及负责粘度计算的虚拟成员函数的实现。源代码中提供了有关实现的更多信息。
新的粘度模型继承了viscosityModel,因此新的粘度模型必须满足清单69中所示的viscosityModel的接口。
//清单69
//- Return the laminar viscosity
virtual tmp<volScalarField> nu() const = 0;
//- Return the laminar viscosity for patch
virtual tmp<scalarField> nu(const label patchi) const = 0;
//- Correct the laminar viscosity
virtual void correct() = 0;
//- Read transportProperties dictionary
virtual bool read(const dictionary& viscosityProperties) = 0;
correct成员函数执行运动粘度的计算(更新),而nu成员函数提供访问。
注:在OpenFOAM中,就像在其他大规模面向对象软件中一样,虚函数的替代实现扩展了库的功能。换句话说,在OpenFOAM中扩展库时,要了解虚函数在其他派生类中的作用,因为这些成员函数也很可能在新类中被修改。
粘度模型扩展从viscosityModel的公共继承和私有数据成员的定义开始,这是粘度计算所必需的,如清单70所示。清单70中的私有成员函数loadViscosityTable负责从CSV文件中阅读实验数据,该数据被转换为标量场rheologyTableX和rheologyTableY,用作OpenFOAM中基于样条的插值的输入。
//清单70
class interpolatedSplineViscosityModel
:
public viscosityModel
{
// Private data
//Dictionary for the viscosity model
dictionary modelDict_;
//x and y entries of the rheology data for
// use with the spline interpolator
fileName dataFileName_;
scalarField rheologyTableX_;
scalarField rheologyTableY_;
tmp<volScalarField> nuPtr_;
// Private Member Functions
// Load the viscosity data table
void loadViscosityTable();
从viscosityModel继承的纯虚成员函数的声明如清单71所示。运动粘度字段是私有数据成员(包装在tmp智能指针中),因此粘度字段和补丁粘度字段可以轻松返回。因此,模型实现的主要部分在于loadViscosityTable并校正。
// 清单71
//- Return the laminar viscosity
tmp<volScalarField> nu() const
{
return nuPtr_;
}
//- Return the laminar viscosity for patch
virtual tmp<scalarField> nu(const label patchi) const
{
return nuPtr_-> boundaryField()[patchi];
}
//- Correct the laminar viscosity
virtual void correct();
//- Read transportProperties dictionary
bool read(const dictionary& viscosityProperties);
csvTableReader类用于读取包含图11.4中实验数据的CSV文件。loadViscosityTable在构造函数体中调用一次,在读取成员函数中调用一次。正确的成员函数从每个单元中的viscosityModel获取应变率,然后使用基于样条的插值法从loadViscosityTable读取的实验数据中插值表观运动粘度。清单72概述了实现。
void interpolatedSplineViscosityModel::loadViscosityTable()
{
csvTableReader<scalar> reader(modelDict_);
List<Tuple2<scalar, scalar> > data;
reader(dataFileName_, data);
// Resize to experimental data
rheologyTableX_.resize(data.size());
rheologyTableY_.resize(data.size());
forAll(data, lineI)
{
const auto& dataTuple = data[lineI];
rheologyTableX_[lineI] = dataTuple.first();
rheologyTableY_[lineI] = dataTuple.second();
}
新粘度模型的定义位于constant/transportProperties字典文件中:
transportModel interpolatedSplineViscosityModel;
interpolatedSplineViscosityModelCoeffs
{
dataFileName "constant/viscosityData/anand2004kinematic.csv";
hasHeaderLine false;
refColumn 0;
componentColumns (1);
}
rho 1060;
新粘度模型的输入包含实验数据文件的路径,以及定义CSV文件结构的信息。CSV文件不包含标题,参考列为0,只有单个组分列1,表观运动粘度来自[1]。
成员函数correct代码如下所示:
void interpolatedSplineViscosityModel::correct()
{
// Interpolate kinematic viscosity in each cell from tabular data.
volScalarField& nu = nuPtr_.ref();
const volScalarField cellStrainRate = strainRate();
forAll(cellStrainRate, cellI)
{
nu[cellI] = interpolateSplineXY
(
cellStrainRate[cellI],
rheologyTableX_,
rheologyTableY_
);
}
nu.correctBoundaryConditions();
}
11.3.1 示例案例
一个下落的“血液”液滴撞击一个无法穿透的壁面是样条粘性模型的例子。 案例本身包含在存储库中,位于
ofbook/ofprimer/cases/chapter11/falling-droplet-2D
两相VoF解算器interIsoFoam [2]用于模拟非牛顿液滴通过空气下落并撞击固体表面。注意,该模拟是二维的并且在空间上是欠分辨的;但它仍然很好地用作示例模拟。正方形区域有三个不可穿透的壁和一个开放大气边界条件,如图11.5所示。可使用需要4个CPU内核的准备好的Allrun脚本运行案例直至完成。
直径为1毫米的液滴从零速度开始,在畴中居中。 重力加速液滴向下,最终冲击无滑移壁面。 当液滴冲击壁面时,高的局部应变率改变了液体中的有效粘度。 非牛顿效应可视化在图11.6。
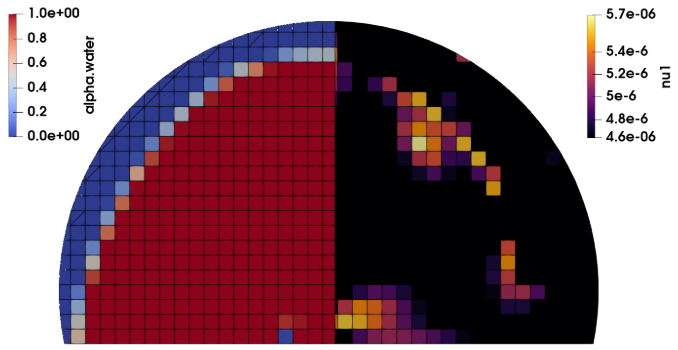
- M Anand and Kr R Rajagopal. “A shear-thinning viscoelastic fluid model for describing the flow of blood”. In: Int. J. Cardiovasc. Med. Sci. 4.2 (2004), pp. 59–68. Url: http://www.cs.cmu.edu/afs/cs.cmu.edu/project/taos-10/publications/MAKRR2004.pdf.
- Henning Scheufler and Johan Roenby. “Accurate and efficient surface reconstruction from volume fraction data on general meshes”. In: J. Comput. Phys. 383 (Apr. 2019), pp. 1–23. Issn: 10902716. Doi: 10.1016/j.jcp. 2019.01.009. ArXiv: 1801.05382. Url: https://www.sciencedirect.com/science/article/pii/S0021999119300269.
- Hermann Schlichting and Klaus Gersten. Boundary-Layer Theory. 8 rd rev. Ed. Berlin: Springer, 2001.
- D. C. Wilcox. Basic Fluid Mechanics. 3 rd rev. Ed. DCW Industries Inc., 2007.
函数对象是编译到动态库中的独立于求解器的代码,可以在仿真时间循环中执行,也可以在仿真完成后由后处理应用程序执行。函数对象通常在模拟运行时执行后处理计算,但也可以操作场或模拟参数。OpenFOAM 函数对象库可包含任意数量的函数对象,这些对象可在运行期间链接到应用程序:OpenFOAM 提供了在每个仿真案例中加载动态库的机制。函数对象的封装功能以预定义方式从求解器中获取,因此函数对象必须遵循固定的类接口。
与传输模型或边界条件一样,OpenFOAM函数对象被实现为类,被组织成类层次结构,并被编译成动态链接库。这允许用户通过配置文件选择任意数量的不同功能对象。OpenFOAM中函数对象的模块化层次结构的另一个好处是能够轻松地与他人共享函数对象库。函数对象实现完全自维持的计算,并且根本不涉及对应用程序代码的任何修改。不必对解算器或实用程序应用程序进行任何更改,也无需重新编译它们即可访问新的函数对象。这改进了遵循“开放-封闭”的OOD模式的代码的可重用性:功能对扩展是开放的,现有的实现对修改是封闭的。
从用户的角度来看,函数对象通常提供不影响求解器求解的功能,它们执行的运行时后处理任务通常应该独立于所选的求解器求解器。它们的目的是实施一般的后处理方法,例如计算任何场变量的平均值,与求解器代码分开。
作为一个假设的例子,考虑一个参数CFD优化研究,将稳态模拟的入口和出口边界之间的压降作为目标函数。使用函数对象,可以在每次迭代之后评估该压降,并且一旦压降满足一些期望的条件就终止模拟。与函数对象相反,使用后处理应用程序将需要完成每个模拟,可能涉及比收敛宏观压降所需的迭代更多的迭代,这取决于求解算法的收敛标准。
本部分介绍了C++和OpenFOAM函数对象(Function Object)的软件设计。 C++和OpenFOAM函数对象之间的差异应该明确,因为它们可能会导致混乱。
12.1.1 C++中的函数对象
详细描述C++中函数对象的实现和用法超出了本书的范围,在文献[2]、[3]和[1]等中有详细描述。本文简要概述了C++函数对象,足以将其与OpenFOAM函数对象区分开来。
正如其名称所示,函数对象是行为类似函数的对象。在 C++编程语言中,当操作符 operator()为其类重载时,其对象的行为就像函数一样。清单74显示了一个非常简化的 C++函数对象示例。重载算术运算符(+、-、*、/)允许类对其对象实现算术操作,尽管实现不限于算术操作。这种 C++语言特性被广泛用于 OpenFOAM 本身的代数场运算。以类似的方式,重载类的 operator()()使其对象具有类似函数的行为。
// list 74
class CallableClass
{
public:
void operator()() {}
};
int main(int argc, const char *argv[])
{
CallableClass c;
c();
return 0;
}
函数对象是对象这一事实带来了不同的优点:
- 函数对象可以存储有关其状态的附加信息。
- 它被实现为一种类型,这是泛型编程中经常使用的事实。
- 它的执行将比涉及传递函数指针的代码更快,因为函数对象通常是内联的。
函数对象可以在处理operator()()中的参数时累积信息,并将累积的信息存储为数据成员以供以后使用。
下面的C++函数对象示例显示了如何实现OpenFOAM类,该类在C++ STL函数对象的帮助下选择网格单元,而不是依赖于OpenFOAM数据结构。此类名为fieldCellSet,可在示例代码存储库的ofBookFunctionObjects文件夹中找到。
OpenFOAM中的网格选择通常是拓扑的,例如选择中心位于球体内的网格的标签。此示例中实现的fieldCellSet类使用volScalarField的场值从网格中收集像元。如果场值满足特定条件,则网格选择器会将特定的网格标签添加到一组标签中。
遵循SRP,通过将单元选择函数定义为根据选择标准参数化的函数模板,将类fieldCellSet与单元选择标准解耦。在下面的两个代码片段中,此模板参数属于泛型类型Collector,参数col存储此类型的对象。因此,fieldCellSet使用模板参数来描述collectCells中的实际选择标准。
//- Edit
template<typename Collector>
void collectCells(const volScalarField& field, Collector col);
fieldCellSet能够与任何实现了operator()()的Collector函数对象一起工作,接受标量值并返回布尔值,这就是它的结果。Collector模板参数的概念可以在collectCells成员函数模板的实现中检查,该模板在文件fieldCellSetTemplates.C中定义:
template<typename Collector>
void fieldCellSet::collectCells
(
const volScalarField& field,
Collector col
)
{
forAll(field, I)
{
if (col(field[I]))
{
insert(I);
}
}
}
如上面的代码片段所示,collectCells成员函数只是对所有场值进行迭代,并期望Collector返回一个布尔变量作为对场值field[I]进行操作的结果。这指定了收集器模板参数概念:
- callable:函数对象是自然选择的
- unary:它必须至少允许一个函数参数
- predicate:它返回一个布尔变量
总而言之,小单元格收集器类fieldCellSet有一个成员函数模板,该模板将volScalarField和函数对象col作为参数。它使用函数对象来检查是否应根据字段的值将单元格添加到单元格集中。但是,如何实现这种比较并不重要,只要实现了col的operator()并返回布尔值即可。
这种简单的实现允许将任何函数对象传递给collectCells成员函数模板。在下面的示例中,使用了STL的函数对象。单个fieldCellSet类的测试应用程序的实现可以在示例代码存储库中找到,位于applications/test子目录下,名为testFieldCellSet。testFieldCellSet中与C++中的函数对象相关的部分是一行代码:
fcs.collectCells(field, std::bind1st(std::equal_to<scalar> (), 1));
collectCells类的对象fcs电泳collectCells方法。
本例中使用的函数对象是equal_to STL函数对象模板。这个通用函数对象只检查类型T的两个值是否相同。由于它使用泛型编程的类型提升方面,因此只能应用于定义了相等运算符==的类型的实例。但是,equal_to函数对象需要两个参数进行比较。剩下的问题是如何在collectCells成员函数模板中为字段值调用它。对于这个简单的例子,答案相当简单:equal_to函数对象的第一个参数已绑定到值1。这意味着testFieldCellSet应用程序应创建一个由场值等于1的所有网格单元组成的单元集合。
面向对象的设计允许fieldCellSet类委托网格标签的存储,以及委托在每个新时间步长执行的输出操作。这是通过多重继承实现的:
class fieldCellSet
:
public labelHashSet,
public regIOobject
{
在上面的代码片段中,labelHashSet是OpenFOAM类模板HashSet的实例化,它使用Foam::label作为关键值。
从regIOobject继承允许类在对象注册表中注册,并在调用时间增量运算符(Time::operator++())时自动写入磁盘。写入以这样一种方式执行,即输出文件包含OpenFOAM稍后重新读取数据所需的必要OpenFOAM文件头信息。
testFieldCellSet应用程序可以在第11章的示例中进行测试,即
/ofprimer/cases/chapter11/falling-droplet-2D
通过以下方式调用:
?> blockMesh
?> setAlphaField
?> testFieldCellSet -field alpha.water
生成的网格集存储在0目录中,要使用paraView应用程序对其进行可视化,必须使用foamToVTK将其转换为VTK格式。在此之前,必须将网格集从0目录复制到constant/polyMesh/sets:
?> mkdir -p constant/polyMesh/sets
?> cp 0/fieldCellSet !$
完成此操作后,网格集将转换为
?> foamToVTK -cellSet fieldCellSet
这将在下落液滴2D案例下生成VTK目录。图12.1显示了初始时间步长的下落液滴单元集的alpha1场。在paraView应用程序中,可以轻松地完成基于区域的网格集的计算和可视化,但关键是要了解C++中的函数对象,以及在编写OpenFOAM代码时如何轻松使用这些对象。C++中的函数对象与扩展函数非常相似。OpenFOAM中的函数对象与C++函数对象具有相似的功能,但它们的设计不同。

12.1.2 OpenFOAM中的函数对象
OpenFOAM中的函数对象具有与标准C++函数对象不同的类接口。它们不依赖于重载operator(),而是使用functionObject抽象类定义的类接口,如清单75所示。因此OpenFOAM函数对象的类层次结构在结构上类似于边界条件(第10章)和传输模型(第11章)所使用的层次结构。抽象基类(functionObject)规定了OpenFOAM中所有函数对象的接口。与重载调用运算符的标准C++函数对象相比,OpenFOAM函数对象使用各种虚函数,使得它们可以在模拟循环的不同步骤中被调用。
// List75
// Member Functions
//- Name
virtual const word& name() const;
//- Called at the start of the time-loop
virtual bool start() = 0;
//- Called at each ++ or += of the time-loop.
// forceWrite overrides the outputControl behaviour.
virtual bool execute(const bool forceWrite) = 0;
//- Called when Time::run() determines that
// the time-loop exits.
// By default it simply calls execute().
virtual bool end();
//- Called when time was set at the end of
// the Time::operator++
virtual bool timeSet();
//- Read and set the function object if
// its data have changed.
virtual bool read(const dictionary&) = 0;
//- Update for changes of mesh
virtual void updateMesh(const mapPolyMesh& mpm) = 0;
//- Update for changes of mesh
virtual void movePoints(const polyMesh& mesh) = 0;
functionObject成员函数的执行与模拟时间的更改或网格的更改有关,如清单75所示。OpenFOAM中的模拟由Time类控制,functionObject的大多数成员函数都与模拟时间的变化有关。因此,Time类负责根据事件调用functionObject成员函数。使用对模拟时间的常量访问,从网格类polyMesh中调用与网格运动(movePoints)和场映射(updateMesh)相关的两个成员函数。
作为这些要求的结果,Time类将为每个特定模拟加载的所有函数对象组合到函数对象列表(functionObjectList)中,如图12.2所示。
functionObjectList实现functionObject的接口,并将成员函数调用委托给复合函数对象。当模拟开始并且Time类的runTime对象初始化时,读取模拟控制字典controlDict。functionObjectList的构造函数读取controlDict并解析函数子字典中的条目。函数子字典中的每个条目定义单个函数对象的参数,然后将这些参数传递给函数对象选择器。选择器(functionObject::New)实现了OOP中已知的“工厂模式”,并在运行时使用字典参数类型初始化functionObject抽象类的具体模型。最后,将选定的函数对象追加到函数对象列表中。该机制还依赖于OpenFOAM中的RTS机制,允许用户针对不同的仿真用例选择和实例化不同的功能对象。
由于函数对象在运行时被初始化,并且依赖于动态多态性(虚拟函数),因此实现主功能的成员函数在解析调用哪个虚拟成员函数时会产生开销(动态调度)。然而,由OpenFOAM函数对象执行的计算所花费的计算时间比动态调度多几个数量级,因此使用动态调度的开销可以安全地忽略。
OpenFOAM中的函数对象也是在模拟过程中执行类似函数操作的对象,因此该属性使其名称合理。functionObject的类声明用作描述进一步差异的另一个示例:
// Private Member Functions
//- Disallow default bitwise copy construct
functionObject(const functionObject&);
//- Disallow default bitwise assignment
void operator=(const functionObject&);
与C++函数对象相反,OpenFOAM中的函数对象禁止赋值和复制构造,因此无法将它们作为值参数传递。禁止的赋值和复制构造对OpenFOAM函数对象没有负面影响:OpenFOAM中函数对象的中心使用点是Time类中的私有属性functionObjectList,因此不需要在列表中手动实例化它们或按值传递它们。
OpenFOAM函数对象的设计及其与Time类的交互已经介绍完毕,剩下的一点就是新函数对象的编程。基本上,任何继承自functionObject的类,实现其接口,并且其类型入口以及必要的参数列在controlDict模拟控制目录中,都将被OpenFOAM解释为函数对象。模拟中初始化函数对象的过程由Time类执行并自动发生,前提是添加了函数对象配置子字典,并且在system/controlDict文件中加载了实现函数对象的动态链接库。然而,在开发新的函数对象之前,建议检查所需的功能是否已经在OpenFOAM或社区贡献中可用。
在开始开发新的功能对象之前,建议检查OpenFOAM或OpenFOAM相关项目中是否已存在类似的功能对象。由Bernhard Gschaider开发的swak4Foam项目包含各种不同的有用函数对象。
本章使用OpenFOAM和swak4foam中的函数对象,使用上一章中的下落液滴示例
ofprimer/cases/chapter11/falling-droplet-2D
12.2.1 OpenFOAM函数对象
OpenFOAM中函数对象的组织在《Extended Code Guide》中有详细描述,因此这里省略了这一信息。
检查OpenFOAM中函数对象源代码的起点是$FOAM_SRC/postProcessing/functionObjects。
OpenFOAM中的函数对象通过模拟文件夹中system/controlDict文件中的相应条目启用。必须在controlDict中指定函数对象和实现函数对象的库所需的参数。
OpenFOAM函数对象的用法可以使用CourantNo函数对象进行演示,该函数对象计算网格中每个单元的Courant数,并将其存储为volScalarField,然后写入,以便可以对其进行视觉检查。要使用courantNumber函数对象,需要定义动态加载的库和2D模拟实例的system/controlDict文件中的函数条目,如清单76所示。
courantNo
{
type CourantNo;
phiName phi;
rhoName rho;
writeControl outputTime;
libs ("libfieldFunctionObjects.so");
}
...
对于courantNo函数对象以及OpenFOAM中的其他函数对象,输出独立于模拟输出。因此,需要附加条目writeControl来规定函数对象的输出控制。将writeControl设置为outputTime将使用与模拟中其他字段的输出频率相同的输出频率写入Courant数。图12.3显示了在0.04秒时使用interIsoFoam解算器模拟的液滴的Courant数分布结果。
实现新的函数对象需要定义functionObject类的类接口,并准备编译函数对象库所需的文件。当实现不同的函数对象时,这些任务会重复执行。为了节省开发时间,OpenFOAM中提供了一个shell脚本,用于生成新函数对象库所需的文件结构。该脚本名为foamNewFunctionObject,它生成目录结构、函数对象类文件(.C和.H)以及包含单个函数对象的函数对象库的基本构建配置。
12.3.1 函数对象生成器
要使用函数对象生成器,请确保已设置OpenFOAM环境。
以下命令使用foamNewFunctionObject脚本创建新的函数对象库:
?> foamNewFunctionObject myFuncObject
?> cd myFuncObject
在OpenFOAM-v2012中,模板文件中存在语法错误,该错误已在主分支上修复。由于本书描述了发布版本,因此应该对生成的函数对象的构造函数进行一个小的修改。行中有括号错误:
Foam::functionObjects::myFuncObject::myFuncObject
(
const word& name,
const Time& runTime,
const dictionary& dict
)
:
fvMeshFunctionObject(name, runTime, dict),
// Bracket error.
boolData_(dict.getOrDefault<bool> ("boolData"), true),
应修改为:
Foam::functionObjects::myFuncObject::myFuncObject
(
const word& name,
const Time& runTime,
const dictionary& dict
)
:
fvMeshFunctionObject(name, runTime, dict),
// Bracket error fixed.
boolData_(dict.getOrDefault<bool> ("boolData",true)),
在这个小的语法修正之后,新的库可以用下面的命令进行编译:
myFuncObject > wmake libso
foamNewFunctionObject脚本为每个函数对象生成一个OpenFOAM库,如myFunctObject/Make/files中所定义:
myFuncObject > cat Make/files
myFuncObject.C
LIB = $(FOAM_USER_LIBBIN)/libmyFuncObjectFunctionObject
该库自动命名为myFuncObjectFunctionObject,并存储在包含用户定义的库二进制文件的OpenFOAM文件夹中。
为我们引入的每个新函数对象生成一个不同的函数对象库是不切实际的,因为这需要在system/controlDict文件中为用foamNewFunctionObject生成的每个函数对象添加一个库条目。可以分类到一个组中的函数对象属于同一个库。为了将foamNewFunctionObject生成的函数对象组织成组,可以使用foamNewFunctionObject生成多个函数对象文件夹结构,并将其编译成单个库。例如,
?> mkdir myFunctionObjects && cd myFunctionObjects
?> foamNewFunctionObject myFuncObjectA
?> foamNewFunctionObject myFuncObjectB
创建两个函数对象myFuncObjecta和,yFuncObjectb,它们应该编译到同一个库myFunctionObjects中。foamNewFunctionObject生成的任何函数对象的make/files选项可以用作库构建配置的开始。 例如,使用来自myFuncObjectB的构建配置,
myFunctionObjects > mv myFuncObjectB/Make .
myFunctionObjects > rm -rf myFuncObjectA/Make
它的make文件夹现在包含需要修改的MyFunctionObjects库的构建配置。 特别地,MyFunctionObject/make/文件应该如下所示:
myFuncObjectA/myFuncObjectA.C
myFuncObjectB/myFuncObjectB.C
LIB = $(FOAM_USER_LIBBIN)/libmyFunctionObjects
它基本上列出了MyFunctionObjects库中两个函数对象容器的两个实现(.C)文件,并指定了新函数对象库的位置(FOAM_RUN && cd ! ?> mkdir myFunctionObjectsTest && cd myFunctionObjectsTest ?> cp -r FOAM_TUTORIALS/incompressible/icoFoam/cavity/cavity . ?> cd cavity
通过system/controlDict文件中的以下条目激活新库myFunctionObjects中的新函数对象myFuncObjectA:
```c++
libs ("libmyFunctionObjects.so");
functions
{
funcA
{
type myFuncObjectA;
}
}
第一行指定应该动态加载的新库。OpenFOAM自动搜索$FOAM_LIBBIN和$FOAM_USER_ LIBBIN以查找可用的库。函数条目是一个字典,可以包含任意多个字典条目,每个条目指定一个不同的函数对象。在上面的代码片段中,funcA子字典配置了myFuncObjectA函数对象。funcA的名称是任意的:任何用户定义名称都是可接受的。
使用blockMesh生成网格并启动icoFoam求解器会导致错误:
--> FOAM FATAL IO ERROR: (openfoam-2012)
Entry 'labelData' not found in dictionary
"path/to/cavity/system/controlDict.functions.funcA"
这是预料之中的:函数对象生成器脚本foamNewFunctionObject准备了一个骨架实现,除了初始化一些伪数据成员(布尔、标签和标量)之外,它什么也未做。如果system/controlDict中未提供这些数据成员的数据,则函数对象将发出抱怨。
另一方面,如果我们错误地命名了函数对象,OpenFOAM会发出警告:
--> FOAM Warning :
Unknown function type myFuncObjectAA
Valid function types :
2(myFuncObjectA myFuncObjectB)
因此,使用函数对象有两种方式可能出错:我们错误地命名了函数对象,或者我们没有提供初始化它所需的数据。 如果我们错误地命名了一个函数对象,求解器将在没有它的情况下运行。 如果缺少初始化函数对象所需的数据项,求解器将不运行,用户将在system/controlDict中输入所需的数据。system/controlDict中funcA子指令的完整定义如下:
functions
{
funcA
{
type myFuncObjectA;
boolData false;
labelData 0;
scalarData 0;
}
}
一旦模板函数对象实现被编译到库中并且可以与求解器一起使用(测试),则可以扩展默认实现。
FoamNewFunctionObject生成的虚拟数据成员:
class myFuncObjectA
:
public fvMeshFunctionObject
{
// Private Data
//- bool
bool boolData_;
//- label
label labelData_;
//- word
word wordData_;
//- scalar
scalar scalarData_;
将取而代之的是数据成员支持新函数的计算对象。成员函数生成的foamNewFunctionObject几乎什么都不做:
bool Foam::functionObjects::myFuncObjectA::read(const dictionary& dict)
{
dict.readEntry("boolData", boolData_);
dict.readEntry("labelData", labelData_);
dict.readIfPresent("wordData", wordData_);
dict.readEntry("scalarData", scalarData_);
return true;
}
bool Foam::functionObjects::myFuncObjectA::execute()
{
return true;
}
bool Foam::functionObjects::myFuncObjectA::end()
{
return true;
}
bool Foam::functionObjects::myFuncObjectA::write()
{
return true;
}
而且应该实现。
12.3.2 实现Function对象
当函数对象实现一个通常有用的计算时,将函数对象的计算封装在一个单独的类中并在函数对象内重用它是有意义的。有时,这种计算与运行时处理能力的分离会导致具有独立关注点的更干净的实现:进行计算的类与处理运行时执行的函数对象类是分开的。当编写新的函数对象时,应该考虑在函数对象中重用OpenFOAM中的现有类,而不是从头开始编写所有的东西,因为这可能会缩短开发时间。在本节的示例中,函数对象类实现计算并从functionObject继承运行时操作。
如上所述,函数对象的成员函数在OpenFOAM中的模拟循环内的特定位置被调用:
- start:在时间循环开始时执行
- execute:当时间增加时执行
- end:在时间循环结束时执行(时间已达到endTime的值)。
在计算在时间循环的开始和结束没有不同的情况下,成员函数开始和结束调用成员函数执行。本节中介绍的函数对象跟踪多相模拟期间包含特定相的所有网格单元。此示例不是特别有用,其唯一目的是演示通常由功能对象执行的计算,包括网格,场与模拟时间控制。
函数对象示例的代码可在的示例代码库中找到:
src/ofPrimerFunctionObjects/phaseCellsFunctionObject
在文本编辑器中查看代码可能有助于理解下面描述的示例。
要开始对库进行编程,请为新函数对象库创建一个名为ofPrimerFunctionObjects的目录,并使用foamNewFunctionObject从模板生成函数对象:
?> mkdir ofPrimerFunctionObjects && cd ofPrimerFunctionObjects
?> foamNewFunctionObject phaseCellsFunctionObject
?> mv phaseCellsFunctionObject/Make .
编辑Make/files,以便将函数对象编译到新库中:
phaseCellsFunctionObject/phaseCellsFunctionObject.C
LIB = $(FOAM_USER_LIBBIN)/libofPrimerFunctionObjects
如果使用了git标签OpenFOAM-v2012,请更正构造函数行中的括号错误:
// Fixed bracket error.
boolData_(dict.getOrDefault<bool> ("boolData", true)),
编译库:
ofPrimerFunctionObjects > wmake libso
然后在下落液滴测试案例上进行测试:
cases/chapter11/falling-droplet-2D
通过将以下条目添加到system/controlDict:
markPhaseCells
{
type phaseCellsFunctionObject;
libs ("libofPrimerFunctionObjects.so");
boolData false;
labelData 0;
scalarData 0;
}
Allrun脚本生成网格并启动模拟,而从模板生成的函数对象最初不执行任何操作。
注:函数对象的实现如下所述,它假定具有C++编程语言的一些先验知识:类/封装、声明与定义、虚函数、继承等。
用于OpenFOAM中的运行时类型选择(RTS)的函数对象的名称由foamNewFunctionObject生成为“name”+“FunctionObject”,其中“name”是给予foamNewFunctionObject的参数。生成的函数对象的类型名可以在phaseCellsFunctionObject. H中更改,从:
//- Runtime type information
TypeName("phaseCellsFunctionObject");
修改为:
//- Runtime type information
TypeName("phaseCells");
此更改需要重新编译库并修改system/controlDict中函数对象子字典中的type属性。
在模拟过程中,计算包含特定相的单元需要以下数据:相指示符的名称(例如,体积分数)、用于确定网格是否包含特定相的容差以及用于标记包含相的网格的indicator字段(作为phaseCellsFunctionObject的私有属性实现),如清单77所示。
// List77
// Private data
//- Time.
const Time& time_;
//- Mesh const reference.
const fvMesh& mesh_;
//- Name of the phase indicator field.
word fieldName_;
//- Reference to the phase indicator.
const volScalarField& alpha1_;
//- Phase cells field.
volScalarField phaseCells_;
//- Phase cell tolerance.
scalar phaseTolerance_;
//- Percent of cells that have contained the phase.
scalar phaseDomainPercent_;
一旦声明了私有属性,就需要由类构造函数初始化它们,如清单78所示。
//List78
phaseCellsFunctionObject::phaseCellsFunctionObject
(
const word& name,
const Time& time,
const dictionary& dict
)
:
functionObject(name),
time_(time),
mesh_(time.lookupObject<fvMesh> (polyMesh::defaultRegion)),
fieldName_(dict.lookup("phaseIndicator")),
alpha1_
(
mesh_.lookupObject<volScalarField>
(
fieldName_
)
),
phaseCells_
(
IOobject
(
"phaseCells",
time.timeName(),
time,
IOobject::NO_READ,
IOobject::AUTO_WRITE
),
mesh_,
dimensionedScalar
(
"zero",
dimless,
0.0
)
),
phaseTolerance_(dict.get<scalar> ("phaseTolerance")),
phaseDomainPercent_(0)
{}
当然,此定义需要在phaseCellsFunctionObject. H中进行相应的声明。phaseCellsFunctionObject的运行时类型选择(RTS)使用上述类型名称:
//- Runtime type information
TypeName("phaseCells");
foamNewFunctionObject应用运行时类型选择(RTS)所需的OpenFOAM宏:唯一可以修改的是上述函数对象的类型名。通过在相关子字典系统/controlDict字典中提供类型条目来选择函数对象。
属性初始化后,实际计算在phaseCellsFunctionObject::execute中实现
bool phaseCellsFunctionObject::execute()
{
calcWettedCells();
calcWettedDomainPercent();
report();
return true;
}
在这里,execute()成员函数的子计算已经被分开。在这个小示例中,这不是必需的。但是,在软件工程中,当函数计算量很大时,这是一种很好的做法,很难理解函数实际上做了什么。将子计算组织成子函数使得实现模块化:可以实现子计算的变化,并且可以利用继承来扩展该类,而不修改现有的实现。此外,将较大的算法组织成子算法,并将它们实现为子函数,可以提高主算法的可读性,如上面的execute()成员函数所示。
calcWettedCells成员函数标记“wetted”的网格:
void phaseCellsFunctionObject::calcWettedCells()
{
forAll (alpha1_, cellI)
{
if (isWetted(alpha1_[cellI]))
{
phaseCells_[cellI] = 1;
}
}
}
在这种情况下:
bool isWetted(scalar s)
{
return (s > phaseTolerance_);
}
被特定相“润湿”的网格百分比计算为:
void phaseCellsFunctionObject::calcWettedDomainPercent()
{
scalar phaseCellsSum = 0;
forAll (phaseCells_, cellI)
{
if (phaseCells_[cellI] == 1)
{
phaseCellsSum += 1;
}
}
phaseDomainPercent_ = 100. * phaseCellsSum / alpha1_.size();
}
该报告将生成到标准输出流,其中:
void phaseCellsFunctionObject::report()
{
Info << "Phase " << fieldName_ << " covers " << phaseDomainPercent_
<< " % of the solution domain." << endl << endl;
}
由于函数对象包含可以在模拟期间写入以供以后检查的数据成员,因此write()成员函数实现为:
bool phaseCellsFunctionObject::write()
{
if (time_.writeTime())
{
phaseCells_.write();
}
return true;
}
这确保了phaseCells场仅以由模拟用户定义并由Foam::Time控制的写入频率写入磁盘。
system/controlDict中函数字典的以下子字典启用函数对象:
markPhaseCells
{
type phaseCells;
libs ("libofPrimerFunctionObjects.so");
phaseIndicator alpha.water;
phaseTolerance 1e-06;
}
这定义了构造函数的字典条目(请参见清单78),以及函数对象的动态链接库。在cases/chapter 11/falling-droplet-2D中执行Allrun会将phaseCells写入磁盘,并在求解程序输出中添加以下内容:
Phase alpha.water covers 5.4 % of the solution domain.
Phase alpha.water covers 5.4 % of the solution domain.
Phase alpha.water covers 5.4 % of the solution domain.
Phase alpha.water covers 5.48 % of the solution domain.
Phase alpha.water covers 5.48 % of the solution domain.
- Andrei Alexandrescu. Modern C++ design: generic programming and design patterns applied. Boston, MA, USA: Addison-Wesley Longman Publishing Co., Inc., 2001.
- Nicolai M. Josuttis. The C++ standard library: a tutorial and reference. Boston, MA, USA: Addison-Wesley Longman Publishing Co., Inc., 1999.
- David Vandevoorde and Nicolai M. Josuttis. C++ Templates: The Complete Guide. 1 st ed. Addison-Wesley Professional, Nov. 2002.
通常,OpenFOAM中有两种主要的动态网格处理功能:网格运动和拓扑变化([4],[5])。网格运动仅涉及网格点的位移,而不改变网格拓扑:网格元素(例如点、边、面和单元)之间的连接。移动网格点看起来似乎是一项相当琐碎的任务,但根据所需的运动,所需的操作可能比预期的更复杂。非结构化有限体积法所使用的几何信息,例如面中心和面区域法向矢量,是从唯一网格点的列表中建立的。因此,网格点的位移触发了非结构化有限体积法所需的几何信息的计算。网格变形后,其值仍与初始网格相关的场需要映射到新网格。这种映射必须应用于以单元为中心和以面为中心的物理场,因为FVM中的物理场值表示单元体积或单元面区域的平均值,并且面和单元可能经历网格细化和粗化的修改。
更改网格拓扑通常包括添加或删除网格元素:点、边、面或单元,这最终会更改网格元素之间的连接。因此,与网格运动相比,涉及拓扑网格改变的操作相当复杂,因为它们涉及更复杂的算法和数据结构。为了获得快速准确的求解,有两个主要问题需要改变拓扑结构:移动网格边界和求解中的大梯度。 当一个物体在域内显著移动,网格点之间存在相对运动时,网格很可能会被过度扭曲或压缩。 这方面的一个例子是活塞在气缸中运动:网格层被添加或删除,网格的部分可以相互分离,然后重新连接。
第二个问题类别要求模拟在那些先验未知的域区域中具有更高的精确度,例如,在网格生成的点上。 对于在模拟域中涉及激波的模拟,其中激波位置是求解过程的一部分,基于例如压力梯度应用拓扑变化来实现激波出现区域的局部静态细化。 另一个不同的例子是在两相模拟中两个不互溶的液体相之间的界面:物理特性在界面上的值突然变化,但在模拟开始时界面位置是已知的。 然而,为了获得更精确的求解,网格在流体界面附近进行局部动态细化。 当界面在计算域中移动时,这种细化跟随界面。
通过将动态网格操作封装到类层次结构中的类中,将动态网格操作保持在较高的抽象级别上,这允许OpenFOAM用户将动态网格操作从流动求解器分离并将其联合收割机。动态网格类也可以使用面向对象的设计原则进行组合,以扩展具有多个动态网格操作的流求解器,从而提高数值模拟的准确性和灵活性。
本章对现有的动态网格类型进行了概述,并对OpenFOAM现有的动态网格引擎进行了更详细的描述。 关于基类的设计和一些选定的动态网格的设计的详细信息可以在13.1节中找到。 对使用动态网格处理感兴趣的读者更感兴趣的是第13.2节,它提供了一些使用示例。 通过结合实体运动和六面体网格细化来扩展OpenFOAM现有的动态网格处理,在13.3节中描述。
动态网格类的设计因每个特定动态网格的功能而异。本章简要概述了OpenFOAM中动态网格的功能和设计,包括网格运动和网格拓扑更改。
13.1.1 网格运动
OpenFOAM中实现的网格运动操作主要有两种类型:实体网格运动和网格变形。
顾名思义,实体运动会置换网格点,同时保持其相对位置。实体网格运动涉及网格的平移和旋转或两者的组合,并且可以将其规定为或计算为对实体动力学建模的常微分方程的解。
与网格运动相反,网格变形将位移从网格边界不均匀地分布到求解域的内部。位移分布采用不同的方法:代数插值或求解点位移或速度的输运(通常是拉普拉斯)方程。
13.1.1.1 实体网格运动
实体网格运动如图13.1所示。在OpenFOAM中,实体运动由各种类定义,所有类都从它们的公共基础派生:实体运动函数。motion函数返回描述物体运动的七元数。此运动是平移向量和旋转四元数的组合。七元数使用相同的向量转换来置换每个网格点。关于四元数的更多信息可以在[2]的书中找到。
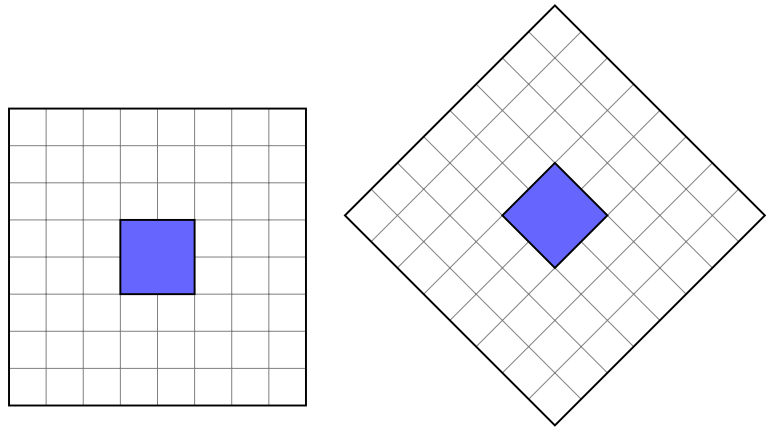
从抽象基类solidBodyMotionFunction派生的类定义存在的运动类型。从简单的运动(如linearMotion和rotatingMotion)到复杂的运动(如tabulatedMotion)(SDA用于船舶耐波性调查)。从图13.1中的UML图中可以看出,solidBodyMotionFunction定义了虚拟方法转换,该转换又由每个派生类实现。它计算用于在初始位置与当前时间的位置之间变换网格点的分隔数,并表示平移与旋转。
转换函数封装在一个类中,该类支持运行时选择和重用。从solidBodyMotionFunction派生的任何类都不会更改网格点的位置,它们只提供转换。
执行实际实体网格运动的动态网格类名为solidBodyMotionFvMesh,它继承自dynamicFvMesh。图13.2中的类图显示了solidBodyMotionFvMesh和solidBodyMotionFunction之间的关系。使用solidBodyMotionFvMesh类的策略模式([1])实现变换函数。因此,实体主体运动功能可由其他数据库零件作为独立图元重复使用。要计算实体运动,类和实体网格运动之间的关系必须未知。此外,solidBodyMotionFunction是使用Strategy模式设计的,允许轻松添加其他函数。只需从solidBody MotionFunction继承,即可使新函数在运行时可选。
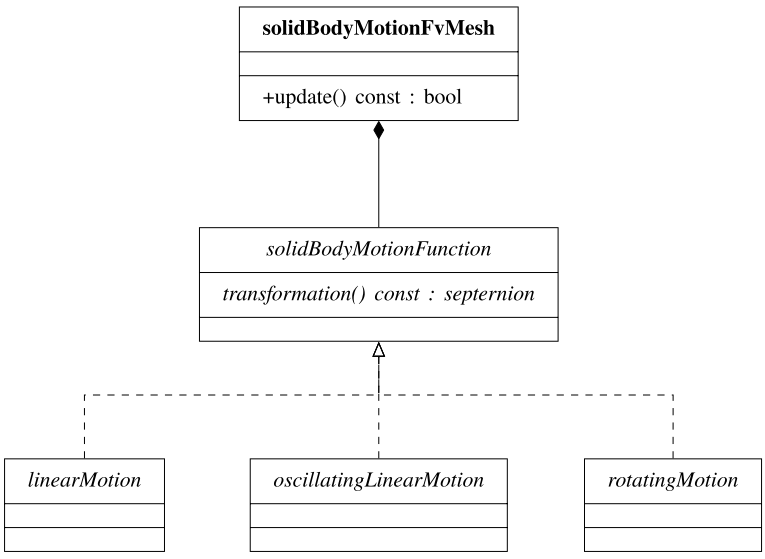
策略模式:在类层次结构中封装各种算法,在客户端(用户)类中组合它们,并使它们在运行时都是可选择的。
另一方面,如果将solidBodyMotionFunction实现为solidBodyMotionFvMesh类中的Template Method模式,则添加另一个网格运动函数将导致多一个动态网格类。模板方法模式应用程序的一个示例是dynamicFvMesh类和派生的动态网格类,它们实现了更新算法。
solidBodyMotionFunction类层次结构的设计是SRP设计原则的一个很好的示例:即使运动函数相当简单,它们也被封装为具有单个简单责任的单独类。运动函数只与计算变换有关,不涉及其他任何内容。此外,运动功能通常可以被组合:例如,可以是,具有恒定旋转的振荡线性运动。在这种情况下,TemplateMethod模式会崩溃,因为它依赖于对动态网格类使用多个继承。
模板方法模式:虚函数用于实现算法,并且(基)类可以提供默认算法实现。因此,衍生类别会实作各种不同的替代算法,在阶层架构中产生每个算法的分支。
solidBodyMotion动态网格使用由用户选定的solidBodyMotionFunction定义的同一分隔数变换网格的所有点或特定部件(即cellZone)。如果未指定cellZone,则使用相同的分隔数移动所有网格点;因此实现了匀速运动。如果在字典中指定了cellZone,则只有cellZone中单元格的点会相应地移动。当物体在转子-定子配置中旋转时,使用滑动界面(AMI/GGI),这就很方便了。除了solidBodyMotionFvMesh之外,还有multiSolidBodyMotionFvMesh,它的功能基本上与solidBodyMotionFvMesh相同,但允许多个运动叠加或作用于不同的单元区域。后者对于两个转子旋转、使用不同单元区和AMI/GGI接口的应用非常重要。使用fvMesh::movePoints将运动本身直接应用于所有相关网格点,因此无需求解额外的方程,这使其成为一种相当快速的方法。
基于网格区域的网格点选择可用于涉及滑动界面的转子-定子网格运动配置。
12.1.1.2 网格变形
网格变形会在网格点之间引入不同的相对运动,从而使边、面和单元变形。网格变形导致的高度扭曲可能会破坏网格的质量。
注:网格质量取决于选择方程离散化的数值方法。有限体积法,最重要的两个mesh-related离散化错误non-orthogonality和偏态误差([3],[6])。
为确保高网格质量,通常仅对网格的一小部分子区域进行强烈变形。相比之下,网格的其余部分的变形保持尽可能低,例如,在网格边界附近。另外,网格变形可以看作是一个优化问题,其中网格的质量表示一个域-全局优化的标量函数。如果将最强位移应用于网格边界的特定部分,则问题仍然是如何将位移传播到网格的其余部分,同时使网格运动不感兴趣的区域中的变形保持最小。在整个求解域中传播网格运动的两种最主要的方法是代数位移插值法和位移的拉普拉斯方程求解法。
位移从网格边界到网格的扩散使用拉普拉斯方程建模: 其中是位移扩散系数,是点位移场。扩散系数在空间上随点与网格边界之间的距离而变化,即: 在方程(13.2)中,是网格点和网格边界之间的距离,并且以使得系数随着与边界的距离而减小的方式规定系数函数。方程(13.1)使用OpenFOAM中的FVM近似。在这种情况下,求解的场以单元为中心,边界场存储在面中心。为了使用FVM计算网格点(单元角点)中的位移,需要执行从单元中心值到网格点的插值。或者,在foam-extend中,方程13.1的解可以使用有限元法(FEM)来近似。
涉及拉普拉斯方程解的网格变形由dynamicMotionSolverFvMesh实现,如图13.3所示。
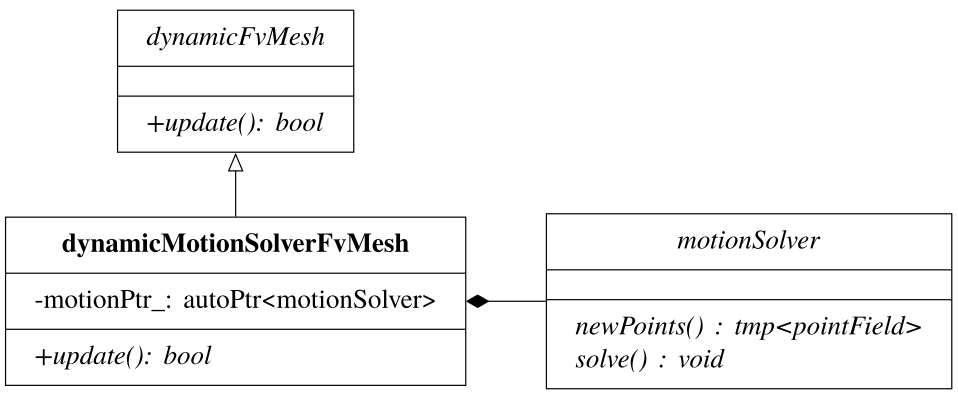
运动物体的运动由其边界描述,这通过将运动边界条件分配给物体边界网格的相应部分来完成。运动边界条件可以作为速度或位移的显式函数给出,或者可以基于外部数据计算。例如,数据驱动的网格运动边界条件可以使用计算的数据来求解由在物体边界上积分的流体力驱动的固体物体运动。
当物体相对于大的解域仅轻微移动时,外部面片的位移通常被设置为固定的零值位移边界条件,该条件基本上固定了空间中这些域边界上的所有点。
一旦用位移(速度)场的边界条件规定了边界运动,运动解算器就承担了在解域内求解运动场的责任。motionSolver在dynamicMotionSolverFvMesh中合成并实现为抽象基类以允许不同的方法来求解运动场(例如,有限体积方程解或位移代数插值)。运动解算器的概念是生成新网格点所必需的,除此之外没有其他要求-网格点的运动随后被进一步委托给父类fvMeshClass:
bool Foam::dynamicMotionSolverFvMesh::update()
{
fvMesh::movePoints(motionPtr_-> newPoints());
if (foundObject<volVectorField> ("U"))
{
volVectorField& U =
const_cast<volVectorField&> (lookupObject<volVectorField> ("U"));
U.correctBoundaryConditions();
}
return true;
}
而运动解算器(motionPtr_)只需要使用newPoints成员函数生成新网格点:
Foam::tmp<Foam::pointField> Foam::motionSolver::newPoints()
{
solve();
return curPoints();
}
调用newPoints会导致修改网面点的网面变形近似。通过求解实现的求解过程将根据使用插值或拉普拉斯方程来传播位移而有所不同。可以使用不同的运动解算器,但描述所有这些解算器超出了范围。
选择位移场的有限体积求解器作为示例,即displacementLaplacianFvMotionSolver。与拉普拉斯有限体积网格运动解算器交互的两个最重要的类如图13.4所示。
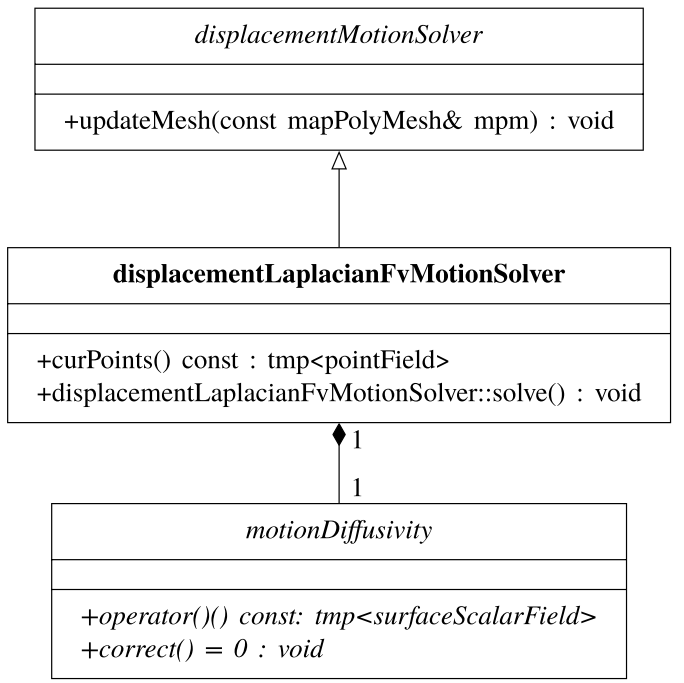
displacementMotionSolver封装网格变形所需的置换场,并提供对其他置换解算器的字段访问。motionDiffusivity是用于计算可变扩散系数的策略(即OpenFOAM模型),由等式13.2给出。然后,该空间可变场可用于缩放位移,该位移通过插值或作为扩散方程13.1中的系数传播到网格的内部。网格运动扩散率的新函数可以很容易地开发出来:从motionDiffusivity继承并将其自身注册到RTS表的类在网格运动框架中自动变为可用。
注:尽管我们在本节中省略了OpenFOAM中网格运动的一些细节,但可用信息应足以理解和扩展网格运动。
由displacementLaplacianFvMotionSolver实现的Laplacian有限体积网格运动解算器(如图13.4所示)在解算成员函数中解算单元中心位移场的扩散方程:
diffusivityPtr_-> correct();
pointDisplacement_.boundaryField().updateCoeffs();
Foam::solve
(
fvm::laplacian
(
diffusivityPtr_-> operator()(),
cellDisplacement_,
"laplacian(diffusivity,cellDisplacement)"
)
);
然后使用反距离加权(IDW)插值法将点位移从单元中心插值到curPoints成员函数内的单元角点(网格点):
volPointInterpolation::New(fvMesh_).interpolate
(
cellDisplacement_,
pointDisplacement_
);
注:每次执行curPoints时(使用基于FVM的运动解算器变形网格时),都会分配一个新的反距离权重插值对象。
创建一个新的IDW插值对象每个时间步是必要的距离反比插值权重变化之间存在相对位移网格点。
13.1.2 拓扑变化
改变网格拓扑包括修改其拓扑信息:添加和删除网格元素(单元、面、边、点)和更新描述网格元素之间相互连接的所有数据结构(例如,边-单元连接列表)。 在网格中应用拓扑变化通常是通过在存在大梯度的区域中提高精度或通过对模拟区域的形状和大小经历极端变化的动力系统进行建模来实现的。 网格变形可能会导致网格质量的严重下降,因为网格面之间的夹角和相邻网格尺寸的比例可以被严重改变。 严重的网格变形导致非结构化FVM的精度损失,因为单元以引入插值、非正交和偏斜误差的方式发生畸变。 网格变形可以与网格拓扑变化耦合以保持精度,从而产生更精确和高效的动态网格引擎。
OpenFOAM中的拓扑变化是以单独的操作来实现的,在设计动态网格类时可以将其凝聚起来。 处理网格拓扑变化的动态网格通常比网格运动类更专业化,因为拓扑变化通常更复杂。 其复杂性在于添加和删除网格单元,改变它们的连通性,并更新场值以解释拓扑变化。 dynamicFVMesh库位于FOAM_SRC/topoChangerFvMesh
以移动的ConeTopoFvMesh为例:它对气缸内运动活塞的动态模拟进行建模。网格沿x轴方向移动面片(网格边界的一部分)。它在网格高度变形的区域中添加和移除细胞层,以保持高网格质量。在OpenFOAM中开发这种专门的动态网格的能力是抽象级别分离的结果。单个拓扑操作在较低的抽象级别上,并且它们的聚集导致在较高的抽象级别上将单元层添加到网格的操作。
图13.5显示了dynamicRefineFvMesh类的重要类关系。与其他动态网格类一样,它实现了update成员函数以符合dynamicFvMesh接口。网格细化操作涉及单元的细化(分割)和取消细化(合并),这取决于上述细化标准。这两个操作分别由两个私有成员函数refine和unrefine实现。每次执行这两个操作中的任何一个时,dynamicRefineFvMesh类都会与父fvMesh类协作,以便更新拓扑操作的物理场。
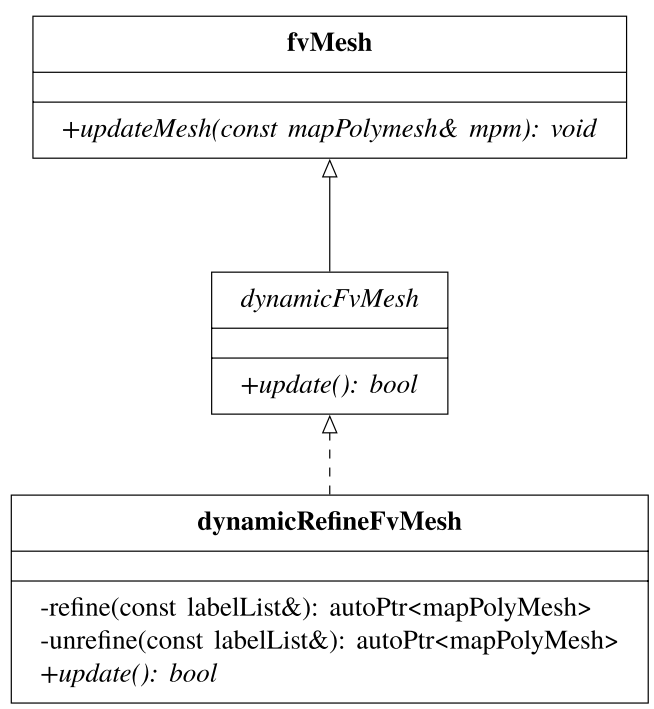
在算法2中,显示了网格细化/取消细化的算法,具有降低的细节水平。Mes细化和取消细化生成拓扑图:将修改的网格元素与原始网格相关联的数据。分割立方体单元的网格面会在OpenFOAM中生成多面体单元:这些单元仍然是立方体的,但是具有多于六个面。
```c++
Read the control dictionary for the dynamicRefineFvMesh.
if not first time step then
Look up the refinement criterion field.
if number of mesh cells < maxCells then
Select cells to be refined (refineCells).
Add cells from the refinement layer and protected cells to refineCells.
if cells to be refined > 0 then
refinementMap = refine(cellsToBeRefined)
update refineCell (refinementMap)
updateMesh (refinementMap)
mark the mesh as changed
end if
end if
select unrefinement points
if number of unrefinement points > 0 then
refinementMap = unrefine (unrefinement points)
updateMesh (refinementMap)
mark the mesh as changed
end if
end if
注意:OpenFOAM中六面体非结构网格的自适应细化不是基于八叉树数据结构的。 网格拓扑被直接改变并存储在新的网格中,使得现有的离散算子和方案能够在拓扑修改的网格上应用。
只要两个相邻单元共享通过分割原始面生成的相同数量的子面,网格的所有者-邻居间接寻址(第1章)将在不修改的情况下工作。然而,重要的是要注意,这种分割引入了非正交性、纵横比和偏斜度误差。因此,通常提供精制细胞的附加层:精细化细胞层的边界应当位于具有小梯度的区域中,在该区域中,高精度不像在精细化网格层内那样重要。
dynamicRefinefVMesh和fvMesh之间的协作是通过调用fvMesh::updateMesh成员函数实现的。 物理场的映射可能是一个复杂的算法来实现。 当实现一个新的拓扑变化类时,通过遵循图13.5中所示的类关系,可以更容易地重用该算法
名称中包含DyMFoam的任何解算器都可以使用OpenFOAM中提供的任何动态网格。前提条件是dynamicMeshDict,它必须存在于模拟实例的常量文件夹中,并且进行正确地配置。
本节提供了两个示例,每个示例都与上一节中描述得网格运动类型相关:使用solidBodyMotionFvMesh的全局网格运动和基于dynamicMotionSolverFvMesh的网格变形。两个示例都使用相同的基本网格,即浸入更大立方体域中的单位立方体。在这两种情况下,内部立方体执行相同的运动,但每个示例计算网格运动的方式不同。这两个示例指定了线性平移运动,并分别使用了solidBodyMotionFvMesh与dynamicMotionSolverFvMesh动态网格类。示例基本案例位于chapter13/unitCubeBase_globalMotion和chapter13/unitCubeBase_patchMotion下的示例案例存储库中。
建立使用动态网格的OpenFOAM案例可能是一项繁琐的工作,尤其是当流动求解器在一个时间步长中占用大量的计算时间时。 工具moveDynamicMesh避免了长时间等待来检查案例是否配置正确:它执行求解者在使用动态网格时所做的所有步骤,而无需昂贵的流求解步骤。 因此,只有mesh.update()在时间循环中执行,该循环触发运行时选择的动态网格类执行的网格修改。 只要运动不依赖于流动模拟得到的任何数据,这种方法就能很好地工作。
使用moveDynamicMesh应用程序扩展具有动态网格操作的模拟实例的速度更快,因为它需要的执行时间比流动求解器短。
13.2.1 全局网格运动
如本节开头所述,可以通过将solidBodyMotionFvMesh与任何选择的solidBodyMotionFunction结合使用来实现全局网格运动。为了实现线性平移运动,在本例中使用linearMotion。与本书中描述的所有其他教程案例类似,第一步是将教程复制到可以安全编辑的位置。为此,请切换到示例案例存储库并找到chapter13目录:
ofprimer > cp -r cases/chapter13/unitCubeBase_globalMotion $FOAM_RUN
ofprimer > run
如果需要更改网格运动,dynamicMeshDict是唯一需要调整的配置文件。从以下摘录中可以看出,它采用solidBody运动解算器定义网格运动类,而linearMotion定义运动函数。
dynamicFvMesh dynamicMotionSolverFvMesh;
motionSolverLibs ("libfvMotionSolvers.so");
solver solidBody;
solidBodyMotionFunction linearMotion;
velocity (1 0 0);
上述字典指示solidBody从linearMotion获取变换,并将其应用于所有网格点,而不是区域。在能够测试运动之前,需要生成网格。因此,请执行以下两个步骤,但请注意,第二个步骤将在案例文件夹中生成时间点目录:
?> blockMesh
?> moveDynamicMesh
第二个调用执行moveDynamicMesh,后者依次处理网格运动,并为每个时间步向屏幕提供多行输出。根据controlDict的配置,时间步长目录以各种频率生成。使用示例案例存储库中的当前案例配置,数据每0.05秒写入一次,并可使用paraView进行检查。第4章描述了如何使用paraView可视化OpenFOAM结果,整个网格仅沿x轴方向移动。
13.2.2 网格变形
与上一节中介绍的全局网格运动示例相比,网格变形在配置工作方面的要求更高。此示例案例的准备版本可在chapter 13/unitCubeBase_patchMotion中找到。添加的constant/dynamicMeshDict负责网格运动,一个新物理场添加到0目录,并且需要在system/fvSolution中插入一个附加的求解器条目。最后两个条目取决于网格运动解算器的类型,在第13.1节中已简要介绍了它们。对于该示例,选择基于位移的网格运动解算器。因此,添加的新物理场名为pointDisplacement,它是一个pointVectorField,需要为此物理场设置相应的边界条件:
dimensions [0 1 0 0 0 0 0];
internalField uniform (0 0 0);
boundaryField
{
"(XMIN|XMAX|YMIN|YMAX|ZMIN|ZMAX)"
{
type fixedValue;
value uniform (0 0 0);
}
HULL
{
type solidBodyMotionDisplacement;
solidBodyMotionFunction linearMotion;
linearMotionCoeffs
{
velocity (1 0 0);
}
}
}
为了说明dynamicMotionSolverFvMesh的功能,不仅为长方体本身定义了运动,还为外部边界指定了速度。该长方体的速度与上一教程中的速度相同,但对于其余面片,速度降低为0.75。当然,这种设置实际上具有有限的执行时间,因为盒子将随着其运动而过多地压缩网格。不过,此设置可作为如何将各种运动指定给不同边界的示例。
前面示例的dynamicMeshdict也需要更改,应该如下所示:
dynamicFvMesh dynamicMotionSolverFvMesh;
motionSolverLibs ("libfvMotionSolvers.so");
solver displacementLaplacian;
displacementLaplacianCoeffs
{
diffusivity inverseDistance (HULL);
}
如前所述,在System/fvSolution中需要一个新的求解器条目。 为此,选择了带有高斯赛德尔平滑器的GAMG型求解器。 必须将以下条目添加到FVSolution的Solvers子字典中:
cellDisplacement
{
solver GAMG;
tolerance 1e-5;
relTol 0;
smoother GaussSeidel;
cacheAgglomeration true;
nCellsInCoarsestLevel 10;
agglomerator faceAreaPair;
mergeLevels 1;
}
通过添加0/pointDisplacement边界文件、fvSolution中的上述条目以及对dynamicMeshDict的所述更改,可以再次执行unitCubeBase示例。
?> rm -rf 0.* [1-9]*
?> moveDynamicMesh
网格变形结果如图13.7所示。
本节涵盖了OpenFOAM求解器与动态网格功能的扩展和新的动态网格类的开发。
13.3.1 在求解器中添加动网格
扩展具有动态网格功能的OpenFOAM解算器是一个相当简单的过程,scalarTransportFoam就是一个例子。由于动态网格处理的扩展需要修改特定的求解器应用程序文件,因此必须复制需要修改的文件。
注:在扩展OpenFOAM解算器时,以及通常在编程时,尽可能减少复制的源代码数量。
复制源代码会增加维护所需的时间。如果原始文件中存在错误,则必须在副本中解决该错误。随着OpenFOAM的发展,不必要的源代码副本使得跟踪上游更改变得困难。此外,复杂的OpenFOAM求解器包含用于初始化全局变量和耦合PDE求解算法的文件。假设复制了整个求解器文件夹,对求解器的修改很小并放置在单个文件中。在这种情况下,很难找出新求解器和原始求解器之间的差异。因此,在编写新的OpenFOAM求解器时盲目复制整个求解器文件夹的“常见”做法从长远来看是低效的。
因此,编程新OpenFOAM求解器的第一步是创建求解器文件夹,并仅将必要的文件复制到求解器文件夹:
?> mkdir scalarTransportDyMFoam && cd scalarTransportDyMFoam
?> cp $FOAM_SOLVERS/basic/scalarTransportFoam/scalarTransportFoam.C .
?> cp -r $FOAM_SOLVERS/basic/scalarTransportFoam/Make .
即使对于相对简单的scalarTransportFoam解算器,也可以重用createFields. H文件。对于更复杂的“真实世界”解算器,可以重复使用更多的解算器文件,从而实现更简洁的实现。通过将路径附加到Make/options,OpenFOAM构建配置文件中的原始求解器,可以启用文件重用:
EXE_INC = \
-I$(FOAM_SOLVERS)/basic/scalarTransportFoam \
-I$(LIB_SRC)/finiteVolume/lnInclude \
-I$(LIB_SRC)/fvOptions/lnInclude \
-I$(LIB_SRC)/meshTools/lnInclude \
-I$(LIB_SRC)/dynamicMesh/lnInclude \
-I$(LIB_SRC)/dynamicFvMesh/lnInclude \
-I$(LIB_SRC)/sampling/lnInclude
EXE_LIBS = \
-lfiniteVolume \
-lfvOptions \
-lmeshTools \
-ldynamicMesh \
-ldynamicFvMesh \
-lsampling
第一个“include”行使用FOAM_SOLVER环境变量指向OpenFOAM的solver文件夹。 如果原始求解器的文件夹包含包含其他必要文件的子文件夹,也可以包括这些子文件夹。 上面代码段中列出的其他行用于包含动态网格头文件和加载动态网格库。
由于此示例创建了一个新解算器,因此应将scalarTransportFoam.C文件重命名为scalarTransportDyMSolver.C,并遵循具有动态网格支持的解算器的OpenFOAM约定。然后,应将Make/files中出现的所有scalarTransportFoam替换为scalarTransportDyMFoam。在Make/files中,将求解器可执行文件编译到$FOAM_USER_APPBIN中,而不是标准$FOAM_APPBIN中,这一点很重要。
与原始解算器相比,处于当前状态的新scalarTransportDyMFoam解算器没有任何新功能。这可以使用第13章/scalarTransportAutoRefine的模拟案例进行测试。
图13.8显示了本例中使用的测试用例的初始条件和域几何。测试用例由一个立方体域组成,初始场预设为域角处的球体,以及用于在空间对角线方向上传输场的恒速场。
验证scalarTransportDyMSolver是否按预期工作后,下一步是在新的解算器中实现动态网格功能。为此,必须在文本编辑器中打开scalarTransportDyMSolver.C,并且必须在simpleControl.H之后包含dynamicMesh.H:
#include "fvCFD.H"
#include "fvOptions.H"
#include "simpleControl.H"
#include "dynamicFvMesh.H"
在主函数中,必须包含createDynamicFvMesh.H而不是createMesh.H,以便启用动态网格:
int main(int argc, char *argv[])
{
#include "setRootCase.H"
#include "createTime.H"
#include "createDynamicFvMesh.H"
#include "createFields.H"
#include "createFvOptions.H"
如果仔细查看scalarTransportFoam的源代码,就会发现没有调用mesh.update(),而mesh.update()负责执行动态网格函数。因此,必须在时间循环结束时添加以下内容:
mesh.update();
runTime.write();
}
Info<< "End\n" << endl;
return 0;
动态网格头文件与相应得库二进制代码必须在构建过程中可用,以便新求解器工作.要包含头文件并链接库,需要通过添加以下“include”行来修改Make/options文件:
-I(LIB_SRC)/dynamicMesh/lnInclude \
-I$(LIB_SRC)/dynamicFvMesh/lnInclude \
通过向Make/options添加以下“链接”行,应用程序与动态网格库链接:
-ldynamicMesh \
-ldynamicFvMesh \
dynamicRefineFvMesh::update成员函数更正网格细化过程生成的新面的体积通量值。此过程称为通量映射,可由用户通过修改放置在常量/dynamicMeshDict中的通量映射表进行管理。有关网格细化的信息,请参见第13.1节。然而,所映射的体积通量是用于流动解算法的足够好的初始猜测,其强制实施体积守恒的体积通量值。对于该示例中的标量输运方程,不需要流动求解算法,因为场是使用恒定的规定速度平流的。
此时编译并运行求解器会得到数值无界解。为了解决这一问题,我们将最后一行代码插入求解器应用程序中,该应用程序模拟了流动求解算法的存在,并计算体积守恒的体积通量值。该行插入到对update成员函数的调用的正下方:
mesh.update();
phi = fvc::interpolate(U) & mesh.Sf();
代码现在可以编译了--通过调用solver文件夹中的wmake。新的求解器可以在
ases/chapter13/scalarTransportAutoRefine
案例文件夹中。图13.9显示了图13.8所示的具有动态自适应网格细化的传输球形标量场T。T的平流是扩散的,网格加密和去加密解决了扩散区域并跟随输送场。
注:通过细化网格,创建了新的单元面,这需要修改体积通量场。体积守恒性、数值有界性以及解的稳定性强烈依赖于体积通量值。
练习:用于该测试用例的细化标准均匀地细化所传输球体的内部。一个有趣的练习是应用一个细化标准,该标准将跟随T值的跳跃。这将降低计算成本并提高精度。
从具有代表性的网格处理类别出发,概述了不同类型的动态网格设计,并对动态网格的使用方法进行了描述,同时对OpenFOAM动态网格处理的求解器进行了扩展,为OpenFOAM发展动态网格处理提供了一个良好的起点。 更复杂的任务,如在OpenFOAM中开发较低层次的拓扑变化并将它们聚集到全新的动态网格类中,更加复杂,超出了本书的范围。
- Erich Gamma et al. Design patterns: elements of reusable object-oriented software. Addison-Wesley Longman Publishing Co., Inc., isbn: 0-201-63361-2.
- R. Goldman. Rethinking Quaternions: Theory and Computation. Morgan & Claypool, 2010.
- Jasak. “Error Analysis and Estimatino for the Finite Volume Method with Applications to Fluid Flows”. PhD thesis. Imperial College of Science, 1996.
- H. Jasak and H. Rusche. “Dynamic mesh handling in openfoam”. In: Proceeding of the 47 th Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, Orlando, Florida. 2009.
- H. Jasak and Z. Tukovic. “Automatic mesh motion for the unstructured finite volume method”. In: Transactions of FAMENA 30.2 (2006), pp. 1–20.
- F. Juretić. “Error Analysis in Finite Volume CFD”. PhD thesis. Imperial College of Science, 2004.
尽管本书涵盖了 OpenFOAM 的许多核心部分,但仍有许多有趣的主题尚未完成,例如新的 FVM 格式和运算符的实现、OpenFOAM 中 Open MPI 的并行编程、为颗粒载流和喷射流开发新的欧拉-拉格朗日模型和方法、开发新的动网格类、为可压缩流开发新的构成定律等等。尽管如此,这些 OpenFOAM 元素的软件设计与本书所涵盖的内容相似,并且基于重复使用贯穿全文的 C++ 编程语言中的少量软件设计模式。透彻理解本书所介绍的材料以及对 C++ 软件设计模式的基本理解,同时不回避实例和练习的实践工作,将为进一步开发 OpenFOAM 奠定坚实的基础。