选择离散格式以及调整线性求解器的控制参数与选择边界条件同等重要。

离散格式在system/fvSchemes中定义，求解器由system/fvSolution字典控制。

3.3.1 数值格式(fvSchemes)

从用户的角度来看，与非结构化有限体积离散和插值相关的所有定义都在system/fvSchemes字典中定义。所需的设置因求解器而异，并取决于数学模型的特定项的公式。在有限体积法的框架内使用离散和插值格式来离散数学模型各项。

在OpenFOAM中，数学模型是使用区域指定语言(Domain Specific Language，DSL)在求解器应用程序中定义的。DSL作为抽象层发展起来，随着时间的推移，算法的实现也越来越高。在其他有关OpenFOAM的信息来源中，OpenFOAM DSL通常被称为公式模拟。在更高级别的抽象中使用算法和公式模拟，允许对数学模型进行非常可读的定义，以及对数学模型进行微不足道的修改。

例如，来自icoFoam求解器应用程序的以下源代码片段显示了动量守恒定律方程的OpenFOAM实现：

fvVectorMatrix UEqn
(
    fvm::ddt(U)
    + fvm::div(phi, U)
    - fvm::laplacian(nu, U)
);
solve(UEqn == -fvc::grad(p));

动量方程的不同项很容易识别、添加、删除或修改。对于这些项中的每一个，都需要在system/fvSchemes中定义等效的离散化。

注：区域指定语言(Domain Specific Language，DSL)是专门为某些应用程序开发的，它是软件开发的自然结果，具有明确的抽象层分离。根据离散化的方程、矩阵和源项而不是迭代循环、变量指针和函数进行思考，这代表了OpenFOAM中的方程模拟/DSL的基础。分离抽象级别是良好软件开发实践的标志。

离散和插值格式是上述源代码中列出的操作的组成部分，其将局部微分方程转化为代数方程，具有有限体积的平均性质。那些参与代数系统组装的项被称为隐式项(implicit terms)，明确计算的项都被称为显式项(explicit terms)。显式项使用来自FVC(finite volume calculus)名称空间的离散运算符进行求值，而隐式项使用来自FVM(finite volume method)名称空间的运算符进行计算。记住这一区别很重要，因为在system/fvSchemes字典文件中为某项定义的离散格式将被用作应用程序代码中的fvc::和fvm::运算符的默认格式。

要获得特定项的支持格式列表，只需用任何单词替换fvSchemes字典文件中的现有格式并执行求解器。求解器返回的错误中会包括按目的选择的名称不存在格式。但是这之后是一个大列表，显示了所有可用的格式。为了获得关于格式参数（方案特定的关键字和值）的信息，用户需要浏览与格式实现相关的源文件。

在求解器应用程序中实现的方程式是在编译时定义的。但是，用于离散化这些方程项的格式的选择是在运行时执行的。这允许用户修改数学模型的离散方式：通过修改system/fvSchemes中的条目，为不同的问题选择不同的格式。

注：离散和插值是OpenFOAM中常用的算法。为了区分隐式算法(矩阵组装)和显式算法(源项)，将算法利用C++命名空间进行分类。命名空间是一种编程语言结构，用于避免名称查找冲突(更多细节见[6])

cavityOscillating的system/fvSchemes字典为：

ddtSchemes
{
    default Euler;
}
gradSchemes
{
    default Gauss linear;
    grad(p) Gauss linear;
}
divSchemes
{
    default none;
    div(phi,U) Gauss linear;
}
laplacianSchemes
{
    default Gauss linear orthogonal;
}
interpolationSchemes
{
    default linear;
}
snGradSchemes
{
    default orthogonal;
}

每个fvSchemes字典都有相同的7个子字典，并且很可能在每个子字典的开头定义了一个默认参数。

将在icoFoam中实现的动量方程的代码片段与上面的清单进行比较，可以看出在此配置中，div(Phi,U)是使用线性方法离散化的。下面概述不同的离散化格式类别，以及所选格式的特点。

注：如果在第一次阅读后，对所选方案的以下描述不清楚，这并不会影响对本书其余部分的理解。感兴趣的读者可以稍后再阅读本书的这一部分，并与第一章一起阅读。在OpenFOAM中描述所有可用的格式超出了本书的范围，因此只讨论了几个选定的格式。

这些格式被分类为与数学模型项以及system/fvSchemes中的条目相关的类别：

• ddtSchemes
• gradSchemes
• divSchemes
• laplacianSchemes
• interpolationSchemes
• snGradSchemes

注：OpenFOAM中的所谓运行时选择(Run-Time Selection)允许在System/fvSchemes中选择不同的格式。如果system/fvSchemes中的条目错误，此模块将输出所有可用格式的列表。这可用于了解可用的格式：输入不存在的格式的名称会提供可用格式的列表。

3.3.1.1 ddtSchemes

ddtScheme是用于时间离散的格式。欧拉一阶时间（Euler first-order temporal）离散格式被设置为瞬态问题的默认值，其恰好是第一章中用来展示FVM离散实践的格式。时间离散化格式的备选方案包括：

• CoEuler
• CrankNicolson
• Euler
• SLTS
• backward
• bounded
• localEuler
• steadyState

在可用的时间离散化方案中，以下将更详细地解释CoEuler和backward。

1、CoEuler

CoEuler格式是一种一阶时间离散格式，既可用于隐式离散，也可用于显式离散。此格式可以自动调整局部时间步长，以便局部Courant数受用户指定的值限制。该格式使用当前时间步长值和从局部Courant数域计算的比例系数来计算局部时间步长。Courant数受限的局部时间步长的倒数计算为： $$\delta t_{fCo}^{-1}=\max \left(C{o}_f/\max Co,1\right)\delta t^{-1}\text{\hspace{1em}(3.1)}$$ 其中，局部面中心Courant数根据体积通量$F$、面法向矢量${\mathbf{S}}_f$及在面$\mathbf{d}$处连接的网格的网格中心之间的距离计算的： $$C{o}_f=\frac{\Vert F\Vert }{\Vert {\mathbf{S}}_f\Vert \Vert \mathbf{d}\Vert }\delta t\text{\hspace{1em}(3.2)}$$ 在提供质量通量的情况下，需要利用密度场来计算局部面中心的Courant数： $$C{o}_f=\frac{\Vert F_{\rho }\Vert }{{\rho }_f\Vert {\mathbf{S}}_f\Vert \Vert \mathbf{d}\Vert }\delta t\text{\hspace{1em}(3.3)}$$ 其中$F_{\rho }$为存储在面中心的质量通量。一旦计算出以面中心的Courant数，就可以使用公式(1)计算时间步长的倒数。对于面中心场${\varphi }_f$，使用面中心的时间步长的倒数来计算一阶时间导数： $$\delta t_{fCo}^{-1}\left({\varphi }_f^n-{\varphi }_f^o\right)\text{\hspace{1em}(3.4)}$$ 由于时间格式主要在网格中心场上操作，因此时间步长的倒数的网格中心值被计算为面中心的最大值，即 $$\delta t_c^{-1}=\underset{f}{\max }\left(\delta t_{fCo}^{-1}\right)\text{\hspace{1em}(3.5)}$$ 其被用来计算网格中心物理场${\varphi }_c$的时间导数： $$\delta t_{cCo}^{-1}\left({\varphi }_c^n-{\varphi }_c^o\right)\text{\hspace{1em}(3.6)}$$ 这样，使用时间步长δt倒数的局部计算场，局部计算时间导数。基于局部Courant数的时间导数的局部估计允许在Courant数较低的流域部分使用较大的时间步长。因此，模拟速度提高了（数值时间在计算域的这些部分人为地加快，因为那里的流动预计会经历较小的变化）。对局部Courant数进行限制，可以增强求解的数值稳定性。

2、backward

二阶后向格式或后向差分格式（BDS2）使用来自当前和两个连续的旧时间步长的物理量的值来组合二阶收敛时间导数。从当前时间开始，使用泰勒级数展开式计算导数，可追溯到两个时间步： $${\varphi }^o=\varphi (t-\delta t)=\varphi (t)-{\varphi }^{\prime }(t)\delta t+\frac{1}{2}{\varphi }^{\prime \prime }\delta t^2-\frac{1}{6}{\varphi }^{\prime \prime \prime }\delta t^3+\dots \text{\hspace{1em}(3.7)}$$

$${\varphi }^{oo}=\varphi (t-2\delta t)=\varphi (t)-2{\varphi }^{\prime }(t)\delta t+\frac{1}{2}{\varphi }^{\prime \prime }4\delta t^2-\frac{1}{6}{\varphi }^{\prime \prime \prime }\delta 8t^3+\dots \text{\hspace{1em}(3.8)}$$

将方程(3.7)乘以4，然后减去方程(3.8)，得到网格中心物理场${\varphi }_c$的BDS2时间离散格式： $${\varphi }_c^{\prime }\approx \frac{\frac{3}{2}{\varphi }_c-2{\varphi }_c^o+\frac{1}{2}{\varphi }_c^{oo}}{\delta t}\text{\hspace{1em}(3.9)}$$

使用旧值计算导数是在OpenFOAM中完成的，不需要客户代码来存储旧的场和网格值。所有的体积场和面心场都有自动存储旧（o）和旧-旧（oo）时间步长值的能力。网格本身也能存储高阶时间离散化所需的信息（如旧的和旧-旧的网格体积场）。由于o和oo场值是已知的，backward格式计算的二阶时间导数可以被显式计算。实际实现时考虑到了时间步长的可能调整，得到以网格为中心的场的导数为： $${\varphi }_c^{\prime }\approx \frac{c_t{\varphi }_c-2c_{t^o}+c_{t^{oo}}{\varphi }_c^{oo}}{\delta t}\text{\hspace{1em}(3.10)}$$ 式中，系数$c$定义为： $$c_t=1+\frac{\delta t}{\delta t+\delta t^o}\text{\hspace{1em}(3.11)}$$

$$c_{t^{oo}}=\frac{\delta t^2}{\delta t^o({\delta }_t+\delta t^o)}\text{\hspace{1em}(3.12)}$$

$$c_{t^o}=c_t+c_{t^{oo}}\text{\hspace{1em}(3.13)}$$

而在两个次级时间步长相等的情况下，$c$系数使用式(9)中的恒定时间步长进行离散化。

3.3.1.2 gradSchemes

梯度格式决定了对求解器中定义的项使用何种梯度计算方式。在实践中有许多例子表明，梯度格式的选择可能会得到更好的计算结果。例如，在两相流模拟中，梯度用于计算表面张力，因此它在由表面张力驱动的流动中起着重要作用。无论何时出现陡峭的梯度，或应用不同的网格拓扑（例如四面体网格），使用更广泛网格模板的梯度格式可能会提供更好的计算结果。

OpenFOAM中可用的梯度格式有：

• Gauss
• cellLimited
• cellMDLimited
• edgeCellsLeastSquares
• faceLimited
• faceMDLimited
• fourth
• leastSquares
• pointCellsLeastSquares

下面选择并描述了其中三种格式：Gauss、cellLimited和pointCellLeastSquares。

1、Gauss

Gauss格式是梯度项、散度项（对流项）和拉普拉斯项（扩散项）最常用的离散格式。第1章也对其进行了描述。此个需要以面心值来计算以体心值的梯度。

2、cellLimited

cellLimited格式扩展了标准梯度格式的功能，其为以网格体心的梯度值计算一个限制器，先以标准方式计算梯度，然后利用限制器对梯度值进行缩放。限制器通过网格体心属性值${\varphi }_c$的最大值与最小值（${\varphi }_{cmax}、{\varphi }_{cmin}$）来构造，该属性是通过间接搜索面相邻网格得到的，如下所示： $${\varphi }_{c\max }={\text{max}}_C\left({\varphi }_c\right)\text{\hspace{1em}(3.14)}$$

$${\varphi }_{cmin}={\text{min}}_C({\varphi }_c)\text{\hspace{1em}(3.15)}$$

式中$\varphi$为网格中心的属性值；$C$为网格$c$的所有网格面相邻网格的集合。一旦得到网格面相邻网格的最小值和最大值，则使用最小值与最大值来计算其与网格体心值${\varphi }_c$的差异： $$\Delta {\varphi }_{max}={\varphi }_{cmax}-{\varphi }_c\text{\hspace{1em}(3.16)}$$

$$\Delta {\varphi }_{min}={\varphi }_{cmin}-{\varphi }_c\text{\hspace{1em}(3.17)}$$

差异值通过用户指定的系数($0<k<1$) 进行缩放： $$\Delta {\varphi }_{max}=\Delta {\varphi }_{max}+(\frac{1}{k}-1)(\Delta {\varphi }_{max}-\Delta {\varphi }_{min})\text{\hspace{1em}(3.18)}$$

$$\Delta {\varphi }_{min}=\Delta {\varphi }_{min}-(\frac{1}{k}-1)(\Delta {\varphi }_{max}-\Delta {\varphi }_{min})\text{\hspace{1em}(3.19)}$$

注意，当用户指定系数$k$为1时，差异值不会进行缩放。

注：本节中的方程依赖于网格与网格之间的连接，它们也使用基于网格的模版。实际的实现是使用owner-neighbor寻址。

限制器初始值设置为1，但当其通过使用h在网格面上循环计算时，其值会被更新。这也是为什么min和max函数将给定的最小值和最大值的属性差与梯度给出的外推差的比率进行比较的原因： $$\Delta ({\varphi }_c{)}_{grad}=\nabla (\varphi {)}_c\cdot \mathbf{cf}\text{\hspace{1em}(3.20)}$$ 这里$\mathbf{cf}$为连接网格体心与网格面中心的向量。之后使用与min/max的值相比增加的差值来计算限制器： $$l=\{\begin{array}{ll}\min \left(l,\frac{\Delta {\varphi }_{\max }}{\Delta {\left({\varphi }_c\right)}_{grad}}\right)& amp;:\Delta {\varphi }_{\max }<\Delta {\left({\varphi }_c\right)}_{grad}\\ \min \left(l,\frac{\Delta {\left({\varphi }_c\right)}_{grad}}{\Delta {\varphi }_{\min }}\right)& amp;:\Delta {\varphi }_{\min }>\Delta {\left({\varphi }_c\right)}_{grad}\end{array}\text{\hspace{1em}(3.21)}$$ 用限制器缩放标准方式计算得到的梯度来确定网格中心点的最终梯度值： $$\nabla (\varphi {)}_c=\nabla (\varphi {)}_c\cdot l\text{\hspace{1em}(3.22)}$$ 3、pointCellsLeastSquares

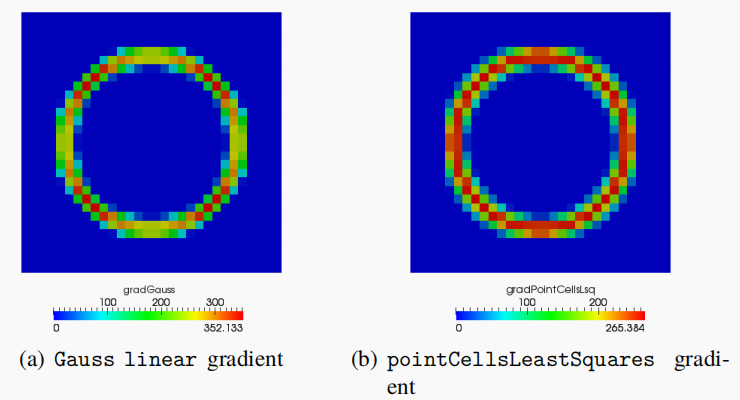
PointCellsLastSquares为梯度提供了更大的模板，其引入相邻的网格单元，这些网格与所讨论的网格相邻，不仅跨网格面，而且跨网格节点。在非结构化六面体网格上，此模板包含$3^3$个网格。虽然在OpenFOAM中实现的数值格式是二阶收敛的，但当流场中出现急剧阶跃时，绝对精度成为数值近似的另一个非常重要的方面。使用更宽的模板，该格式提供了梯度估计，且绝对误差较低。若对网格中心$c$的属性$\varphi$进行线性泰勒展开，可以得到： $$\varphi (\mathbf{x})={\varphi }_c-\nabla (\varphi {)}_c\cdot \left(\mathbf{x}-{\mathbf{x}}_{\mathbf{c}}\right)+O\left({\Vert \mathbf{x}-{\mathbf{x}}_c\Vert }^2\right)\text{\hspace{1em}(3.23)}$$ 计算三个未知变量（梯度$\nabla (\varphi {)}_c$的三个分量）需要三个值。最小二乘梯度涉及将泰勒级数（方程式3.23）从计算梯度的网格中心扩展到相邻网格。展开次数与网格模板的大小成正比。对于二维三角形网格，可以直接从相邻模板的周围三个网格计算梯度。但是，在模板中包含更多的网格可以提高梯度的绝对精度。当已知三个以上的点值时，系统会变得过渡确定。因此，使用最小平方梯度误差计算梯度，定义为： $$E=\sum _{cc}{w}_{cc}^2{E}_{cc}^2\text{\hspace{1em}(3.24)}$$ 其中$cc$是模板的网格。$w_{cc}$是与所讨论的网格和模板网格相关的加权因子。通常将两个网格之间的反向距离作为权重，$E_{cc}^2$是从计算梯度的网格到模板网格的泰勒展开的平方误差： $$E_{cc}=\frac{1}{2}\nabla \nabla (\varphi {)}_c:(\Delta \mathbf{x}\Delta \mathbf{x})\text{\hspace{1em}(3.25)}$$ 经过一些代数处理([4])，使平方误差最小化，得到梯度分量的线性代数系统。由于系统尺寸为3×3，因此对每个单元的线性代数系统尺寸进行组装和求解。此外，由于系数矩阵是对称张量，因此通过直接反转每个网格的系数矩阵来获得解。作为使用此梯度方案的动机，考虑图3.3，其中体积分数场的梯度是使用标准Gauss linear和新的PointCellsLastSquares梯度格式计算的。体积分数场设置为半径R=2cm的圆，中心位于6×6 cm的区域内，使用具有30×30体积的网格进行离散化（[1]）。PointCellsLastSquares计算圆形液滴的梯度比Gauss linear计算得到的更均匀，因为梯度计算中涉及到点邻域。点邻域的参与提高了具有急剧阶跃的场的绝对精度。

提示：图3.3中示例字段所示的高斯梯度计算是网格各向异性的教科书示例-计算强烈依赖于面相对于坐标轴的方向。

提示：作为练习，尝试计算不同网格上陡峭显式函数的梯度，并比较不同梯度格式的误差收敛性。

3.3.1.3 divSchemes

divScheme用于离散数学模型中的对流（散度）项。散度项最常使用的空间离散格式是Gauss离散格式，其使用高斯散度定理。离散格式是FVM的基础，因为它生成了一个代数方程组，这使得不太可能在配置文件中更改隐式项。此外，可为涉及稳态或部分收敛解的模拟提供有界选项，其中$\nabla \cdot (\mathbf{U})$在求求解法的迭代过程中不完全满足。在这种情况下，从系数矩阵中扣除$\nabla \cdot (\mathbf{U})$以提高计算收敛性。

3.3.1.4 laplacianSchemes

system/fvSchemes字典中的laplacianSchemes子字典由Gauss离散和interpolation格式组合而成。Gauss离散是扩散（拉普拉斯）项离散的基本选择，用户可以选择interpolation格式。

3.3.1.5 interpolationSchemes

interpolationSchemes修改面心值的插值方式。不同的插值格式可与空间离散格式一起选择，例如Gauss离散格式。另一方面，可以使用更大的点-值对集合对面上的值进行插值，从而提高插值的精度，然后将使用Gauss离散格式使用面插值来离散散度项、拉普拉斯项或梯度项。

OpenFOAM在interpolation格式方面提供了多种选择：biLinearFit、blended、clippedLinear、CoBlended、cubic、cubicUpwindFit、downwind等。大多数可用的插值格式用于离散对流项。应用特定的数值格式会在对流项中引入不同的数值误差，尤其是当对流特性在解域中发生阶跃时。例如众所周知中心差分格式（CDS，线性）会在解中引入数值不稳定性，而迎风差分格式（UDS，迎风）会人为地平滑对流场（[2]，[7]）。因此，开发了不同的数值格式来抵消原始格式的负面影响，要么涉及高阶插值，要么将最终插值计算为其他插值方案获得的值的组合。

3.3.2 求解控制（fvSolution）

数学模型的离散构造了形为$\mathbf{Ax}=\mathbf{b}$的代数方程组。该系统可以使用直接法或迭代方法来完成。正如[2]所指出的，当求解大型稀疏矩阵时，直接方法的计算成本非常高。与此类矩阵方程的求解过程相关的所有设置，以及压力-速度耦合都在system/fvSolution中完成。根据使用的求解器，该文件的内容会有所不同。

对于前面使用icoFoam求解器的cavity案例，其fvSolution字典的预设定义为：

solvers
{
    p
    {
        solver          PCG;
        preconditioner  DIC;
        tolerance       1e-06;
        relTol          0.0;
    }
    U
    {
        solver          PBiCG;
        preconditioner  DILU;
        tolerance       1e-05;
        relTol          0;
    }
}

PISO
{
    nCorrectors     2;
    nNonOrthogonalCorrectors 0;
    pRefCell        0;
    pRefValue       0;
}

此字典文件中共包含两个子字典：solver与PISO。所有求解器都需要包含solver子字典，因为其包含所使用的各种矩阵求解器的选项和参数。将矩阵求解器与实现特定数学模型的求解器应用程序区分开来很重要。第二个字典存储PISO压力-速度耦合算法所需的参数。OpenFOAM中还有其他压力-速度耦合算法，如SIMPLE和PIMPLE。它们中的每一个都需要在fvSolution中提供一个具有特定算法名称的字典。

提示：OpenFOAM中有两种类型的求解器：solver应用程序和线性求解器。solver应用程序是最终用户直接用于运行仿真的程序。线性求解器是用于求解线性代数方程组的算法，是模拟求解过程的一部分。通常，求解器应用程序简称为solver，因此从现在起，此术语用于求解器应用程序。

3.3.2.1 Linear Solver

上述示例使用PCG求解压力方程，并使用DIC对矩阵进行预处理，DIC可用于对称矩阵。另一方面，对于动量方程，使用非对称PBiCG求解器和DILU预处理器。

无论矩阵求解器是什么，都可以定义以下参数：

tolerance。定义求解器的退出标准。这意味着，如果从一个迭代到下一个迭代的变化低于该阈值，则认为求解过程充分收敛并停止。例如，在对稳态问题进行稳态模拟时，容差应非常小，以提高收敛性和准确性。另一方面，对于瞬态问题，无法获得稳态解，因此容差不能选择得非常小。

relTol。将相对容差定义为求解器的推出标准。若将此参数设置为非零值，则会覆盖tolerance设置。tolerance定义了两次迭代之间的绝对变化，而relTol定义了相对变化。值0.01将强制求解器在两次连续迭代之间迭代知道达到100%的变化。当模拟强非稳态问题且容差设置导致高迭代次数时，使用此参数较为方便。

maxIter。一个可选参数，其默认值为1000。定义了迭代的最大次数，直到求解器停止为止。

3.3.2.1 压力-速度耦合

根据所选的求解器应用程序，将在相应的求解器中实现不同的压力-速度耦合算法。求解器应用程序尝试读取fvSolution中的子字典，具体取决于实现的压力-速度耦合算法。

提示：有关各种算法的更多背景信息，请参阅[2，7]。OpenFOAM wiki上也有大量可用信息。

无论如何都必须定义一些参数：

nNonOrthogonalCorrectors：此参数定义了许多内部循环，用于校正网格的非正交性。当使用四面体网格或在六面体网格上应用局部动态自适应网格细化时，此参数是必需的。[3]和[2]详细描述了非正交性对方程离散化的影响。由于校正是显式的，所以引入了内部循环。它需要多次应用，因为每个应用程序都会减少错误，并且不会完全消除错误。

pRefPoint/pRefCell：这些选项中的任何一个都定义了假定参考压力的位置。pRefPoint采用网格坐标系中的向量，而pRefCell仅采用压力所在网格的标签。对于多相流，该点应始终由任一相覆盖，且不在其间变化。仅当压力未通过任何边界条件固定时，才需要这些参数。

pRefValue：定义参考压力值，通常为零。

特定压力-速度耦合算法或求解器可能需要其他参数。求解器越复杂，fvSolution中通常需要的选项就越多。求解器教程通常提供足够的信息来运行案例。