基础理论

本文描述代数方程组求解中的两种基础迭代法：雅可比迭代法与高斯-赛德尔迭代法。 1 雅克比迭代法 代数方程组可以写成矩阵形式： 若系数矩阵的对角线元素不为0，则第一个方程可以用来求解，第二个方程可以用来求解，以此类推。该方法的第一步是给未知向...

赞(4)胡坤2022-10-12CFD阅读()去评论

本文介绍TDMA算法。 1 TDMA算法介绍 三对角矩阵算法（TDMA）也称托马斯算法，用于求解具有三对角线系数矩阵的代数方程组。其一般形式为： 对于本书中采用的网格布置，指的是图中所示的网格点位置。 图 一维网格布局 对于，可以根据来求解...

赞(4)胡坤2022-10-11CFD阅读()去评论

本文描述高斯消去法的基本处理思路。 有限体积法离散得到的线性方程组可以表示为下面的矩阵方程形式： 式中为单元系数构成的矩阵；为未知量构成的向量；为源项构成的向量。 式(1)矩阵形式为： 一般来说，矩阵中的每一行都表示计算域中某一单元上定义的...

赞(2)胡坤2022-10-08阅读()去评论

编程计算二维热传导问题。 通过手工编制程序巩固学习扩散项离散方式。 1 二维热传导问题 如图所示为一个厚度为 1 cm 的板。板材的导热系数为 k = 1000 W/m.K。西侧边界施加500 kW/m2 的稳定热通量，南侧边界和东侧边界为...

赞(4)胡坤2022-09-30阅读()评论(1)

手撸一个简单的二维稳态热传导问题。 注：案例取自《The Finite Volume Method in Computational Fluid Dynamics》，F.Moukalled。公式显示不全时可左右滑动公式。 ” 1 问题 如图...

赞(2)胡坤2022-09-26阅读()去评论

在如下图所示的二维问题中，给定以下量：，，，。 流动稳定且密度均匀且等于 1。计算和  的动量方程由下式给出： 其中系数，，网格尺寸。利用SIMPLE算法计算、及。 估计网格C的压力值 利用估计的压力值计算速度 根据密度与网格尺寸...

赞(3)胡坤2022-08-27阅读()去评论

一个简单的案例描述SIMPLE算法的使用流程。 SIMPLE算法采用分离方式求解压力速度耦合方程。其基本步骤包括： 假设压力场与速度场 利用假设的压力场，求解动量方程计算得到速度场 利用满足动量方程的速度场更新质量流量，得到 利用新的质量流...

赞(9)胡坤2022-08-25阅读()去评论

一维热传导方程为： 式中，为场变量；为时间；为介质扩散率。 前面的课程中使用的FTCS格式中，对时间项采用的向前差分格式只有一阶精度，我们可以想办法构造更高精度的时间格式，如本文后面将要使用的Runge-Kutta方法。 1 离散方程 Ru...

赞(0)胡坤2021-12-28阅读()去评论

一维热传导方程为： 式中，为场变量；为时间；为介质扩散率。传热方程描述了介质中场变量温度随时间的演化。 热传导方程的离散有多种方法，如有限体积法[11]、有限差分法[12]、有限元法[13]、谱方法[14]等。本文研究的是对所有偏微分方程(...

赞(2)胡坤2021-12-27阅读()评论(1)

CFD Julia是一个编程模块，其包含了从一维传热方程到二维不可压缩Navier-Stokes流动问题的Julia程序设计。这是个利用Julia撸CFD的基础教程，适合作为计算流体力学课程的课后作业。 Julia是个不错的计算机程序设计语...

赞(0)胡坤2021-12-26阅读()去评论

本文利用Julia计算方腔顶盖流动。 密闭空腔中的流体流动满足下面的控制方程： 1 离散方程 离散U动量方程： 离散v动量方程： 离散压力泊松方程： 改写为迭代式的形式。 2 初始值与边界值 初始条件下，计算区域内。 对于边界条件： y=2...

赞(0)胡坤2020-10-18阅读()去评论

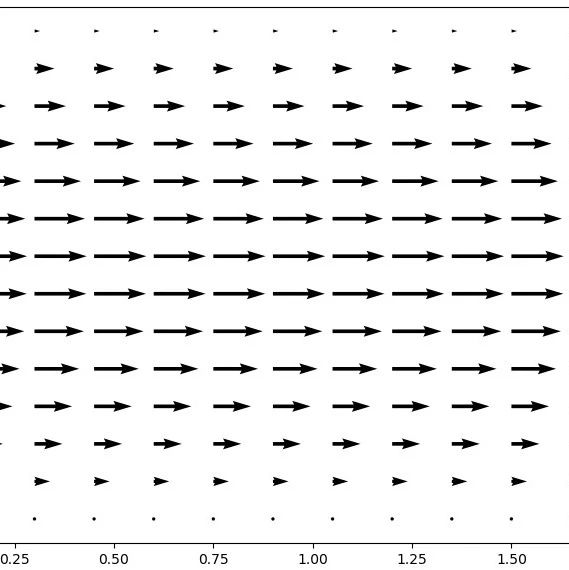
本文利用Julia计算二维管道内压力驱动流动。 管道内压力驱动流动的控制方程如下： 与方腔流动唯一的区别在于U动量方程中多了一个源项F，以模拟压力驱动的影响。 1 离散形式 u-动量方程的离散形式为： 离散v动量方程： 离散压力泊松方程： ...

赞(0)胡坤2020-10-18阅读()去评论

二维拉普拉斯方程为： 拉普拉斯方程通常采用中心差分进行离散。离散方程为： 整理为迭代形式： 注： 拉普拉斯方程是一个稳态模型。 ” 计算区域内部初始条件，边界条件为： 对于此边界条件和初始条件，可以有解析解： 代码 using PyPlot...

赞(0)胡坤2020-10-17阅读()去评论

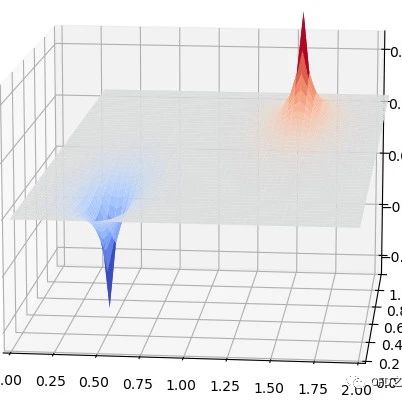
Poisson方程的表达式为： 与Laplace方程不同，Poisson方程带有源项。 1 方程离散 Poisson的离散方式与Laplace方程类似： 改成迭代式形式为： 2 初始值与边界值 假设计算区域初始条件下。四个边界上。 对于源项...

赞(0)胡坤2020-10-17阅读()去评论

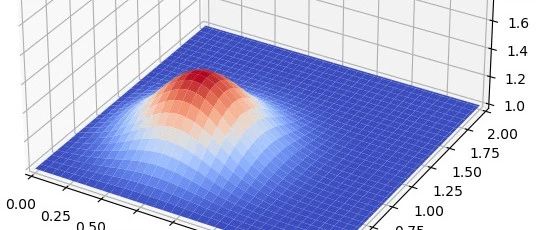
二维扩散问题控制方程可写出下面形式： 这里时间项采用向前差分，空间项均采用中心差分，很容易写出离散方程： 同样写出待求项： 初始条件及边界条件见代码。 using PyPlot nx = 101ny = 101nu = 0.2dx = 2 ...

赞(0)胡坤2020-10-16阅读()去评论

二维Burgers方程描述为： 对其进行离散，可表示为： 整理成迭代形式为： Julia代码 using PyPlotmatplotlib.use("TkAgg") nx = 41ny = 41nt = 120c = 1dx = 2 / (...

赞(0)胡坤2020-10-16阅读()去评论

前面的案例大多数是一维的问题，从现在开始我们进入二维的世界。 事实上将一维问题扩展到二维甚至三维都是非常简单的，采用相同的思路。在2D空间中，结构网格可定义为： 注： 注意这里所提到的结构网格，我们在后面还会详细介绍。 ” 因此，可定义一阶...

赞(0)胡坤2020-10-15阅读()去评论

本文描述利用Julia计算二维非线性对流问题。 二维非线性对流控制方程为： 这里时间项采用向前差分，空间项采用向后差分，离散方程可写成以下格式： 式中，i为x方向角标，j为y方向角标，n为时间项角标。 可得待求项： 采用初始条件： 其他位置...

赞(0)胡坤2020-10-15阅读()去评论

本文简单描述Julia中的数组操作。 1 数组操作 在计算量集中的程序中，使用numpy内置的函数操作能够有效地提高计算性能。下面来举一个例子，考虑到CFD中经常会遇到如下的迭代式： 假设给定初始值，可以通过迭代计算得到的值。 采用迭代方法...

赞(0)胡坤2020-10-13阅读()去评论

本文描述利用Julia求解计算一维扩散方程。一维扩散方程为： 与前面方程不同的地方在于此方程包含二阶导数，因此首先对二阶导数进行离散。 采用中心差分格式对二阶导数进行离散。 考虑泰勒展开式： 两式相加，可得到二阶导数项： 改变排列顺序，可得...

赞(0)胡坤2020-10-11阅读()去评论