
Fluent Meshing案例|05 面网格重构
本案例演示利用Fluent Meshing对导入的STL几何文件进行面网格重构,以方便后续的体网格生成。 案例几何模型如下图所示。 在划分网格过程中需要关注的内容包括: 捕捉大区率区域,如图中的High Curvature 捕捉小的gurn...

本案例演示利用Fluent Meshing对导入的STL几何文件进行面网格重构,以方便后续的体网格生成。 案例几何模型如下图所示。 在划分网格过程中需要关注的内容包括: 捕捉大区率区域,如图中的High Curvature 捕捉小的gurn...

本案例描述Fluent Meshing中边界面网格清理工具的使用方法。 1 启动Fluent Meshing 启动Fluent Launcher,选择选项Meshing ,同时设置Working Directory,如下图所示,点击Star...

本文演示在Fluent Meshing中导入CAD几何模型并生成流体计算网格的基本流程。 启动Fluent Launcher,选择使用Meshing,设置Working Directory 1 导入几何 选择菜单File → Import ...

本案例演示利用Fluent Meshing读入网格并对网格进行操纵处理过程。 案例目的: 以Meshing模式启动Fluent 读取及附加.msh网格文件 使用不同的选项显示几何和网格 理解几何显示及修改功能按钮 1 启动Fluent Me...

懒得写字了,直接放视频好了。 利用SCDM生成三维分块映射网格。分别采用自顶向下及自底向上的方式构建块,构建块的方便程度比起ICEM CFD还是略有不足。 (完) 本篇文章来源于微信公众号: CFD之道

本案例演示Fluent Meshing的传统操作流程(outline View)的基本操作方式。 案例导入其他网格软件生成的面网格,在Fluent Meshing中对导入的面网格进行检查及重构,并生成体网格。Fluent Meshing支持...

Rocky的最新版本中提供了两个颗粒破碎模型:Ab-T10模型及Tavares模型。如下图所述为利用Ab-T10破碎模型仿真颗粒落锤试验。 AB-T10破碎概率模型基于Vogel和Peukert[1]提出的模型及Shi和Kojovic[2]...

年前说翻译一本书《The OpenFOAM® Technology Primer》,后台不断有道友询问进度状态,这里统一回复一下。 目前全书第一遍初步翻译已经完成。得益于当前机器翻译技术的发展,第一遍翻译非常顺利,稍微麻烦点儿的是公式录入。...
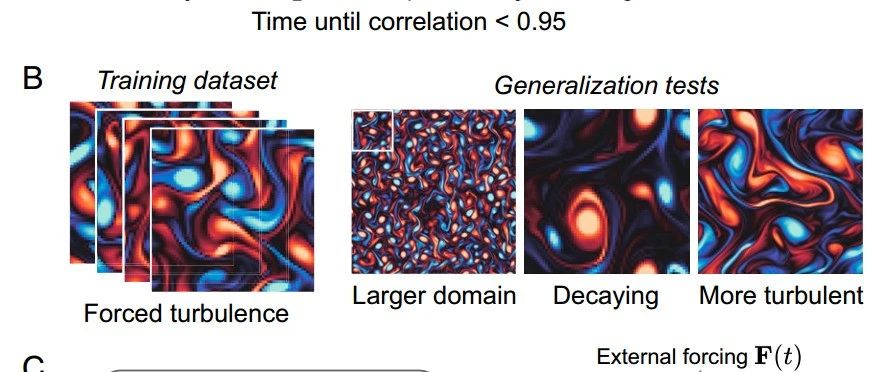
谷歌JAX-CFD论文:《Machine learning–accelerated computational fluid dynamics》 论文地址:https://www.pnas.org/doi/10.1073/pnas.21017...

ANSYS中用于CFD前处理的工具众多,几何处理有DM和SCDM,网格生成有ANSYS Meshing、ICEM CFD与Fluent Meshing。 简单聊聊个人对这些模块的感觉。 1、ANSYS Design Modeler(DM) ...

最近在重新录制【Fluent验证案例】,目前已经全部录制更新完毕。虽然案例大多比较简单,但在录制过程中还是碰到了不少的问题,其中遇到最多的问题是收敛问题。有些案例参数设置很简单,但计算的时候死活就是不收敛甚至发散。这里总结一下常用的收敛控制...

这阵子在找一款能自动识别视频中的语音并生成字幕的软件,想着给录制的课程添加字幕。还别说,得益于这些年AI技术的迅猛发展,还真找到了不少能打的软件。 Adobe Premiere Premiere可谓是视频编辑的大佬了,功能极为强大,作为视频...

流体流动和传热问题的数值解只是近似解。除了在求解算法的开发过程中可能引入的误差之外,在编程或设置边界条件时,数值解总是包括三种系统误差: 建模误差(Modeling errors)。定义为实际流量与数学模型精确解之间的差异 离散误差(Dis...

【Fluent验证案例】系列课程最初录制于2019年,基于Fluent19.0版本,案例模型数据取自Fluent验证文档。 2019年至今,时间已过4年,环境发生了较大的变化: 软件版本。当前Fluent版本已更新至2023R1版,软件操作...

CFD理论类的教材很多,国内的和国外的都比较多,经典也不少。不过下面这本可以说是经典中的经典了。 说的是这本Joel H.Ferziger等的《Computational Methods for Fluid Dynamics》。 这本书目前...

本案例利用STAR CCM+仿真计算旋转腔体内速度分布,并对计算结果进行验证。 1 案例描述 参考资料:J.A. Michelsen. “Modeling of Laminar Incompressible Rotating Fluid F...

本案例利用STAR CCM+计算并验证管道内多组分气体混合。 1 案例概述 参考资料:W.M. Kays and M.E. Crawford. Convective Heat and Mass Transfer. 3rd Edition. ...

本文描述利用SCDM脚本绘制方程曲线的基本方法。 早期版本的SCDM中可以利用参数方程绘制曲线,然而新版本已经找不到此功能了,只能绘制三维方程曲面。不过仍然可以使用脚本绘制参数曲线。 先新建一个设计 打开脚本功能 二维曲线 输入下面的程序代...

魔幻的2022年,暑假从6月中旬一直放到10月中旬,然后在不足三个月的时间里还被封控了两次,后面就藏在家里牧羊。 整个下半年似乎都是宅在家里头划水摸鱼~ 希望2023年一切都会好起来~ (完) 本篇文章来源于微信公众号: CFD之道

接前文Fluent 2023R1更新内容(1)。 9 涡轮机械 在某些问题中,通过将计算模型的大小减小到单通道,Phase-lag边界条件现在可用作求解加速格式。 傅里叶系数的累积和后处理现在可用于瞬态涡轮机模拟中。 新版本中,气动阻尼计算...
有哥有这个模型的原始图吗