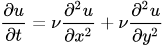
这里时间项采用向前差分,空间项均采用中心差分,很容易写出离散方程:
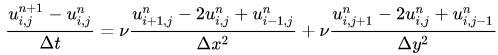
同样写出待求项:
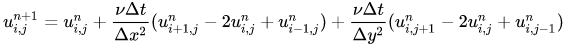
初始条件及边界条件见代码。
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
nx = 31 # 定义x方向节点数
ny = 31 # 定义y方向节点数
nt = 17 # 定义时间步长
nu = 0.05 # 定义扩散系数
dx = 2/(nx-1) # 定义x方向网格尺寸
dy = 2/(ny-1) # 定义y方向网格尺寸
sigma = 0.25 # 定义库朗数
dt = sigma * dx * dy /nu
x = np.linspace(0,2,nx) # x取值范围
y = np.linspace(0,2,ny) # y取值范围
# 定义边界条件
u = np.ones((ny,nx))
un = np.ones((ny,nx))
# 定义初始条件
u[int(.5 / dy):int(1 / dy + 1),int(.5 / dx):int(1 / dx + 1)] = 2
# 绘制初始条件
fig = plt.figure()
ax = fig.gca(projection='3d')
X, Y = np.meshgrid(x, y)
surf = ax.plot_surface(X, Y, u, rstride=1, cstride=1, cmap=cm.viridis,
linewidth=0, antialiased=False)
ax.set_xlim(0, 2)
ax.set_ylim(0, 2)
ax.set_zlim(1, 2.5)
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
plt.show()(屏幕左右滑动可查看完整代码)
初始条件如下图所示。
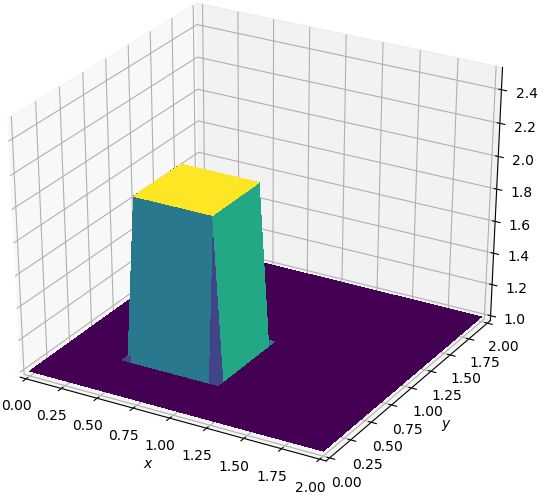
# 定义函数进行求解
def diffuse(nt):
u[int(.5 / dy):int(1 / dy + 1),int(.5 / dx):int(1 / dx + 1)] = 2
for n in range(nt + 1):
un = u.copy()
u[1:-1, 1:-1] = (un[1:-1,1:-1] +
nu * dt / dx**2 *
(un[1:-1, 2:] - 2 * un[1:-1, 1:-1] + un[1:-1, 0:-2]) +
nu * dt / dy**2 *
(un[2:,1: -1] - 2 * un[1:-1, 1:-1] + un[0:-2, 1:-1]))
u[0, :] = 1
u[-1, :] = 1
u[:, 0] = 1
u[:, -1] = 1
fig = plt.figure()
ax = fig.gca(projection='3d')
surf = ax.plot_surface(x, y, u[:], rstride=1, cstride=1, cmap=cm.viridis,
linewidth=0, antialiased=True)
ax.set_zlim(1, 2.5)
ax.set_xlabel('$x$')
ax.set_ylabel('$y$')
plt.show()
diffuse(10)
图形如下图所示。
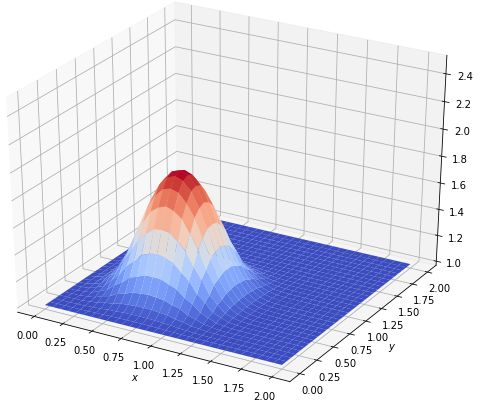
diffuse(14)
计算结果如下图所示。
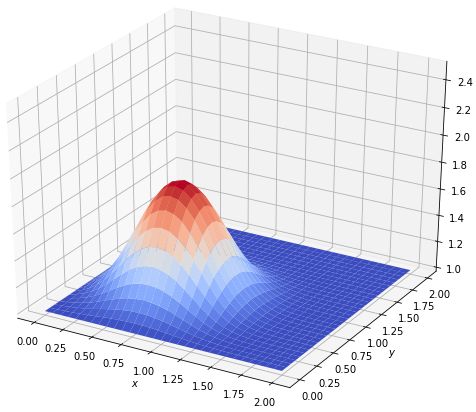
diffuse(50)
如下图所示。
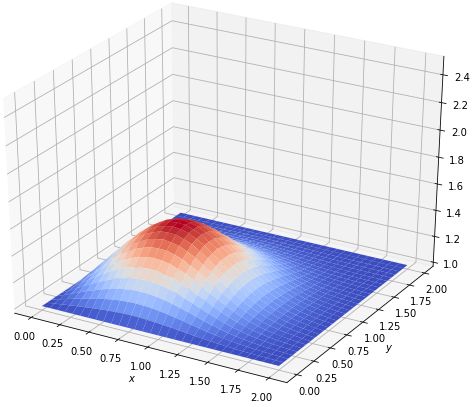
以上代码在jupyter lab中运行通过。
END
本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册