前面的案例大多数是一维的问题,从现在开始我们进入二维的世界。
事实上将一维问题扩展到二维甚至三维都是非常简单的,采用相同的思路。在2D空间中,结构网格可定义为:
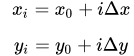
注意这里所提到的结构网格,我们在后面还会详细介绍。
因此,可定义一阶差分格式:
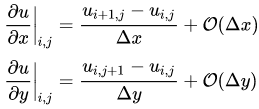
下面来处理二维线性对流方程。
二维线性对流控制方程为:
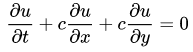
这里时间项采用向前差分,空间项采用向后差分,离散方程可写成以下格式:
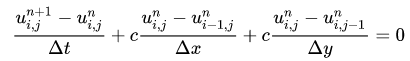
式中,i为x方向角标,j为y方向角标,n为时间项角标。
可得待求项:
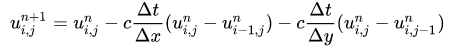
采用初始条件:
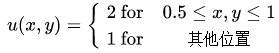
边界条件:
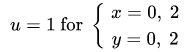
先用代码将初始条件和边界条件表达出来。
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm
nx = 81 #x方向网格数量
ny = 81 #y方向网格数量
nt = 100 #时间步
c = 1 #常数
dx = 2 / (nx - 1)
dy = 2 / (ny - 1)
sigma = 0.2
dt = sigma * dx
x = np.linspace(0,2,nx)
y = np.linspace(0,2,ny)
u = np.ones((ny,nx))
un = np.ones((ny,nx))
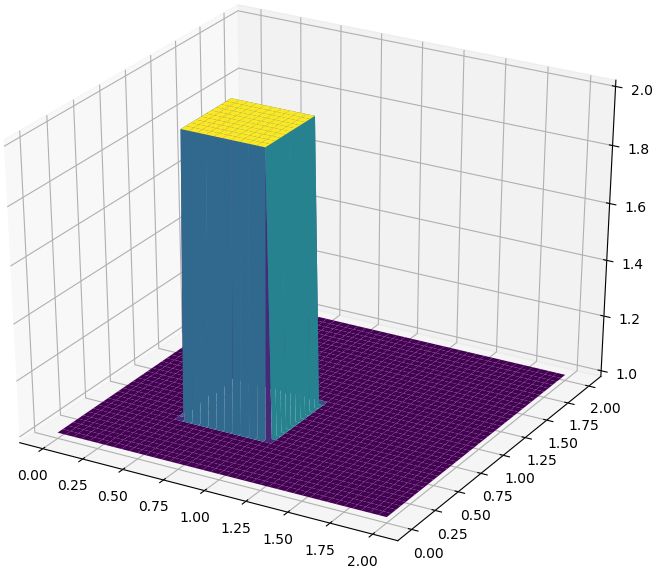
u[int(0.5/dy):int(1/dy+1), int(0.5/dx):int(1/dx+1)] = 2
# 绘制初始条件
fig = plt.figure(figsize=(12,8))
ax = fig.gca(projection='3d')
x,y = np.meshgrid(x,y)
surf = ax.plot_surface(x,y,u[:],cmap = cm.viridis)
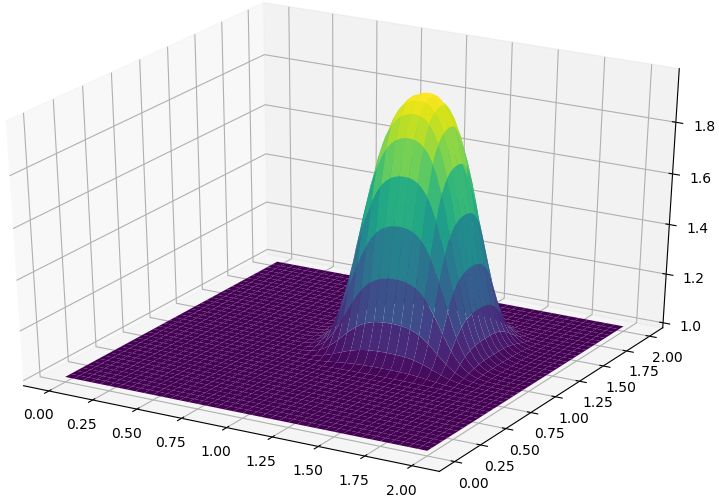
plt.show()初始条件如下图所示。
下面开始迭代计算。我们可以分别采用循环和数组操作来实现,自己体会他们计算时间上的区别。
for n in range(nt + 1): ##loop across number of time steps
un = u.copy()
row, col = u.shape for j in range(1, row):
for i in range(1, col):
u[j, i] = (un[j, i] - (c * dt / dx * (un[j, i] - un[j, i - 1])) -
(c * dt / dy * (un[j, i] - un[j - 1, i])))
u[0, :] = 1
u[-1, :] = 1
u[:, 0] = 1
u[:, -1] = 1
fig = plt.figure(figsize=(11, 7), dpi=100)
ax = fig.gca(projection='3d')
x,y = np.meshgrid(x,y)
surf2 = ax.plot_surface(x, y, u[:], cmap=cm.viridis)
plt.show()计算结果如下图所示。
利用for循环计算速度很慢,下面改用数组运算试试。
for n in range(nt + 1): ##loop across number of time steps
un = u.copy()
u[1:, 1:] = (un[1:, 1:] - (c * dt / dx * (un[1:, 1:] - un[1:, :-1])) -
(c * dt / dy * (un[1:, 1:] - un[:-1, 1:])))
u[0, :] = 1
u[-1, :] = 1
u[:, 0] = 1
u[:, -1] = 1
fig = plt.figure(figsize=(11, 7), dpi=100)
ax = fig.gca(projection='3d')
x,y = np.meshgrid(x,y)
surf2 = ax.plot_surface(x, y, u[:], cmap=cm.viridis)
plt.show()相同的计算结果,如下图所示。
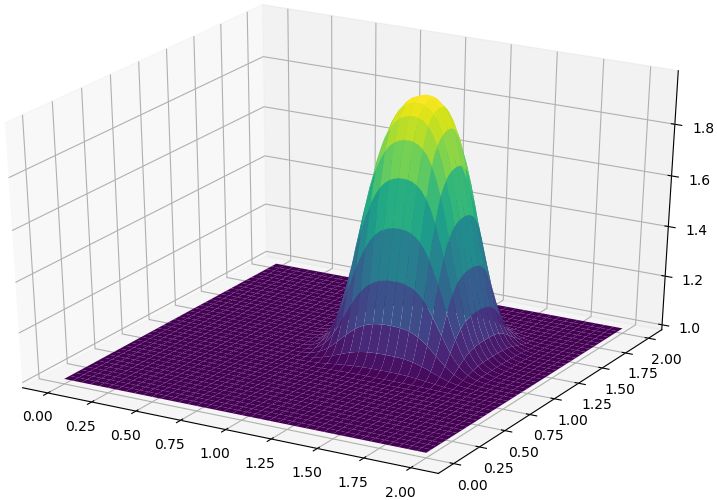
本案例中,利用for循环所需的计算时间约为数组运算的400倍。
给大家推荐一本神书《批判性思维》

本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册