随便在网上翻一翻，都可以发现到处都在讲Python的计算效率很低。我们前面的案例运算量都很小，因此没有什么感觉。今天来聊一聊如何利用数组运算提升Python的计算效率。
前面的案例中大量采用了Python数值计算包numpy，然而并未使用到numpy的性能。numpy的数值计算实际上调用的是c语言操作，按道理计算速度应该不会慢才对。
在计算量集中的程序中，使用numpy内置的函数操作能够有效地提高计算性能。下面来举一个例子，考虑到CFD中经常会遇到如下的迭代式：
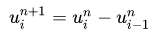
假设给定初始值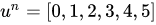
，可以通过迭代计算得到
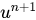的值。
采用迭代方法的代码可写成以下形式。
import numpy as np
u = np.array([0,1,2,3,4,5])
un= u.copy()
for i in range(1,len(u)):
print(u[i] - u[i-1])输出结果为：
1
1
1
1
1其实可以改用numpy内置数组操作来实现，代码写成以下形式。
import numpy as np
u = np.array([0,1,2,3,4,5])
print(u[1:] - u[0:-1])输出结果为：
[1 1 1 1 1]两者结果一致。这里采用numpy数组分片功能来进行计算，来看看u[1:]与u[0:-1]到底是多少。
import numpy as np
u = np.array([0,1,2,3,4,5])
print(u[1:])
print(u[0:-1])输出结果为：
[1 2 3 4 5]
[0 1 2 3 4]可以看到u[1:]取的是第2个元素到最后一个元素的值，而u[0:-1]取得的是第1个元素到倒数第2个元素的值。
这样做有什么用呢？对于大量密集计算来讲，这样做能节省大量的计算时间，下面来用一个复杂案例进行测试。
测试案例采用二维稳态导热问题，其控制方程为拉普拉斯方程：
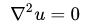
采用二阶中心差分，离散方程可写成：
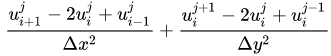
很容易得到：
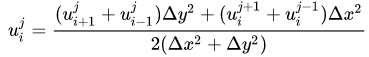
不说二话，直接上代码。
import numpy as np
import matplotlib.pyplot as plt
import time
dx = 0.1
dy = 0.1
dx2 = dx*dx
dy2 = dy*dy
def laplace(u):
nx,ny = u.shape
for i in range(1,nx-1):
for j in range(1,ny-1):
u[i,j] = ((u[i+1,j]+ u[i-1,j]) * dy2 + + (u[i,j+1]+u[i,j-1])* dx2) /(2*(dx2+dy2))
def mat_laplace(u):
u[1:-1,1:-1]= ((u[2:,1:-1]+u[:-2,1:-1])*dy2 + (u[1:-1,2:] + u[1:-1,:-2])*dx2) / (2*(dx2+dy2))
def calc(N,Niter=100):
u = np.zeros([N,N]) #全局初始化
u[0] = 1 #边界条件
for i in range(Niter):
laplace(u)
return u
def mat_calc(N,Niter = 100):
u = np.zeros([N,N])
u[0] = 1
for i in range(Niter):
mat_laplace(u)
return u
# 运行测试
start = time.clock()
U = calc(100,3000)
end = time.clock()
time_elapsed = end - start #普通计算耗时
start = time.clock()
U = mat_calc(100,3000)
end = time.clock()
time_elapsed1 = end - start #数组计算耗时
plt.pcolormesh(U)
plt.show()
plt.legend()
print(time_elapsed)
print(time_elapsed1)计算结果如图所示。
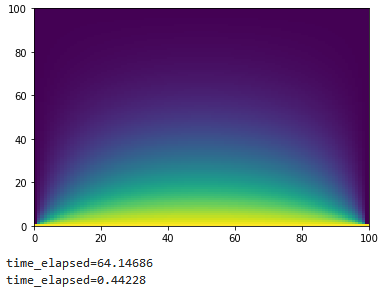
END
本篇文章来源于微信公众号: CFD之道
评论前必须登录！
注册