本次利用Python求解Burger方程。关于Burgers方程的具体描述,可以参阅维基百科。一维Burgers方程描述为:
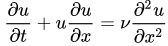
该方程同时包含了对流项与扩散项,式中u为速度,ν为介质粘度。
对时间项采用向前差分,对空间项采用向后差分,二阶导数项采用中心差分,可写成离散方程为:
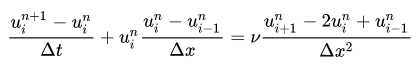
将待求项提出来,可写成:
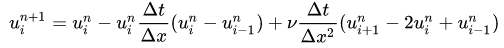
本次采用的初始条件为:
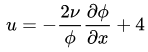
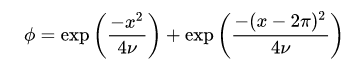
采用边界条件为:
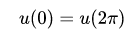
方程解析解为:
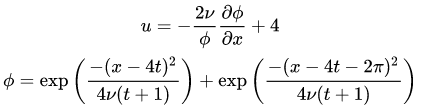
可以利用Sympy包进行符号运算,类似Mathematica软件。
这里的初始条件并非显式表达式,需要将其表达为显式表达式。
故采用Sympy进行简化。
import numpy as np
import sympy
x, nu, t = sympy.symbols('x nu t')
# 定义phi的表达式
phi = (sympy.exp(-(x - 4 * t)**2 / (4 * nu * (t + 1))) +
sympy.exp(-(x - 4 * t - 2 * sympy.pi)**2 / (4 * nu * (t + 1))))
# 计算phi的偏导数
phiprime = phi.diff(x)
from sympy.utilities.lambdify import lambdify
# 得到u的表达式
u = -2 * nu * (phiprime / phi) +4
# 定义lambdify函数,将其写成python可计算的形式
ufunc = lambdify((t,x,nu),u)下面定义初始条件。
from matplotlib import pyplot
nx = 101 # 网格数量
nt = 100 #数据步数
dx = 2 * numpy.pi / (nx - 1) # 网格尺寸
nu = 0.07 # 粘性系数
dt = dx * nu # 时间步长,这么算实际上是为了满足CFL条件
x = np.linspace(0, 2 * numpy.pi, nx) # 计算区域0~2 pi
un = np.empty(nx)
t = 0
u = np.asarray([ufunc(t, x0, nu) for x0 in x]) # 定义初始值
plt.plot(x,u,lw=3,color='red')
plt.xlim([0,2*np.pi])
plt.xlabel("x(m)")
plt.ylabel("time(s)")
plt.ylim([0,10])
plt.show()初始速度分布如图所示。
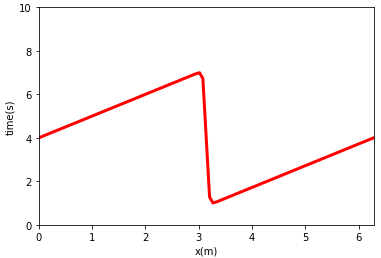
回到Burgers方程上来。
for n in range(nt):
un = u.copy()
for i in range(1, nx-1):
u[i] = un[i] - un[i] * dt / dx *(un[i] - un[i-1]) + nu * dt / dx**2 *
(un[i+1] - 2 * un[i] + un[i-1])
u[0] = un[0] - un[0] * dt / dx * (un[0] - un[-2]) + nu * dt / dx**2 *
(un[1] - 2 * un[0] + un[-2])
u[-1] = u[0]
u_analytical = np.asarray([ufunc(nt * dt, xi, nu) for xi in x])
plt.figure(figsize=(8,4.8))
plt.plot(x,u, marker='o', lw=3, label='Computational')
plt.plot(x, u_analytical, label='Analytical',lw=3)
plt.xlim([0, 2 * np.pi])
plt.ylim([0, 10])
plt.xlabel("x(m)")
plt.ylabel("time(s)")
plt.legend()计算结果如图所示。
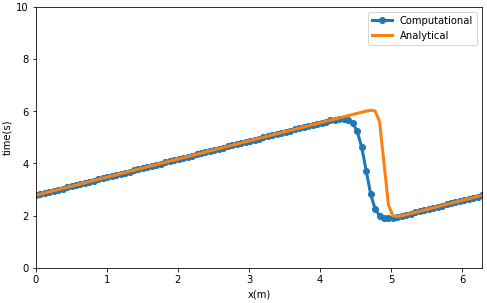
可以看到,误差很大,我们在后续的文章中会提到如何改进算法以减小误差。
这个系列的教程来自LorenaABarba教授在波斯顿大学的教学资料12 step to Navier-Stokes,不要再留言问了。有童鞋留言说Python计算效率低,建议用Julia,其实这里要说的是,Python如果经过优化(比如说上面的代码中的各种for循环),效率也不会低的,后面会提到这个问题。Julia正在学,而且这个语言还很年轻,以后有机会再来个Julia版,其实计算机语言很简单的说,我们的重点应该在离散方法上。

本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册