本文描述利用Python求解计算一维扩散方程。
一维扩散方程为:
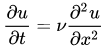
与前面方程不同的地方在于此方程包含二阶导数,因此首先对二阶导数进行离散。
采用中心差分格式对二阶导数进行离散。
考虑泰勒展开式:
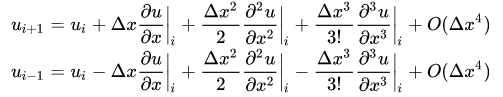
两式相加,可得到二阶导数项:
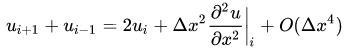
改变排列顺序,可得到:
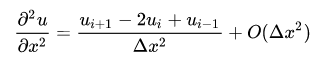
将二阶导数项代入到原方程中,可得到离散方程:
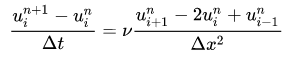
改变方程形式,可得到:
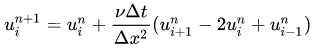
假设初始条件:
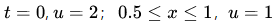
注:这里定义一个sigma的目的是为了控制时间步长dt,以使其满足CFL条件。
令:
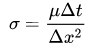
得到:
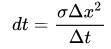
这里的σ就是Courant数。
可写代码如下:
import numpy as np
import matplotlib.pyplot as plt
nx = 41 # 网格节点数
dx = 2/(nx - 1) # 网格尺寸
nt = 40 # 时间步数
nu = 0.3 # 扩散系数
sigma = 0.2 #定义一个中间变量,用于确定时间步长dt
dt = sigma * dx**2 / nu #时间步长
# 定义初始条件
u = np.ones(nx)
u[int(0.5 / dx):int(1 / dx + 1)] = 2
un = np.ones(nx) # 定义一个定义数组
plt.ion()
plt.show()
for n in range(nt): #时间循环,计算每一个时间点上网格点上的数据
plt.cla()
un = u.copy()
for i in range(1,nx-1): #空间循环,计算u[i]
u[i] = un[i]+ nu *dt /dx**2 * (un[i+1] -2 * un[i] + un[i-1])
# 下面为图形绘制代码
plt.plot(np.linspace(0,2,nx) , u , 'm' , lw =3 ) #绘制速度随时间变化曲线
plt.ylim(0.9,2.1) # 确定y轴上下限
plt.title("times: %.4f s"% (n*dt)) # 将时间打印到图形上
plt.pause(0.1) #控制图形显示时间
plt.ioff()
plt.show()代码运行如图所示。
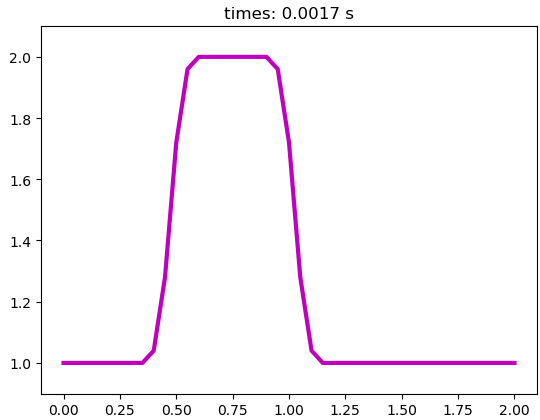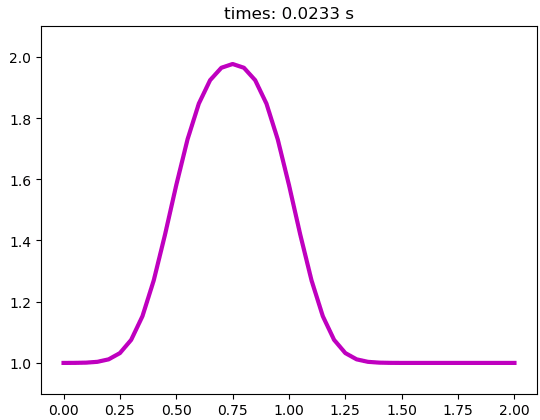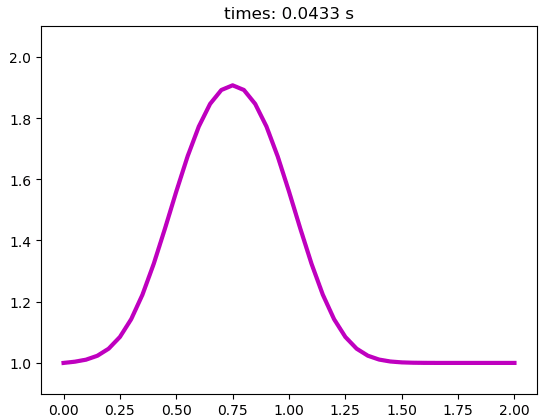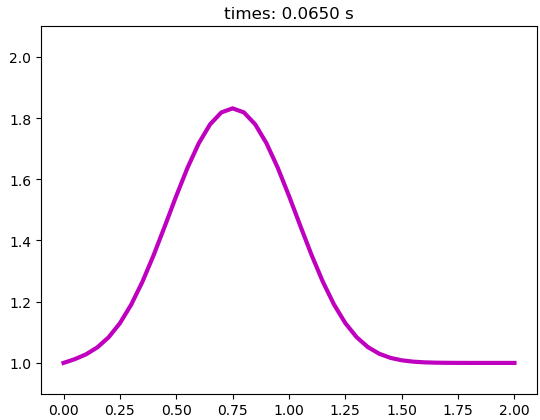
本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册