在前面【Python-CFD】02:线性对流方程中,所采用的计算参数是固定的(具有固定的时间步长和网格尺寸),下面尝试着更改这些参数,看看对于计算结果是否存在影响。
还是用上次的代码做测试,为了方便测试,对代码进行简单封装,代码如下(相同的代码,这里就不注释了):
import numpy as np
import matplotlib.pyplot as plt
def linearconv(nx):
dx = 2/(nx -1)
nt = 20
dt = 0.025
c = 1
u = np.ones(nx)
u[int(0.5/dx):int(1/dx+1)] = 2
un = np.ones(nx)
plt.plot(np.linspace(0,2,nx),u,'b',lw=3,label='origin')
for n in range(nt):
un = u.copy()
for i in range(1,nx):
u[i] = un[i]- c* dt / dx * (un[i] - un[i-1])
plt.plot(np.linspace(0,2,nx),u,'r',lw=3,label='current')
plt.legend()
plt.show()下面通过改变网格尺寸(即dx的数量),来观察计算结果。
linearconv(41) #网格数为41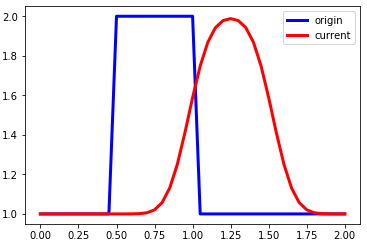
这里用step1的参数计算结果作为参考,这里可以看到,波形存在较大的扩散,随时间推移,波形与初始形状偏离严重。
linearconv(61)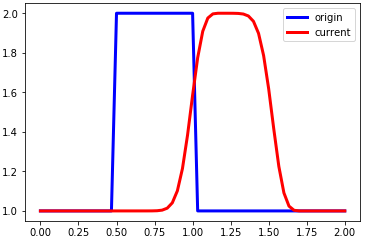
可以看出,随着网格数量增加,波形失真在减小。
linearconv(71)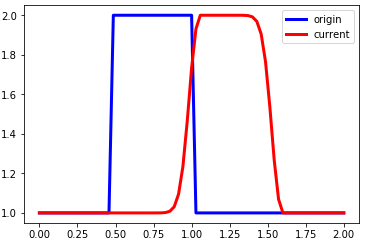
波形与初始形状越来越接近。
linearconv(81)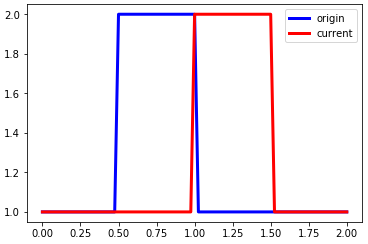
随着网格数量增加,波形失真越来越小,可以认为是计算越来越精确。
linearconv(91)
发生了什么情况,计算已经完全偏离了初始波形,出现了错误。这其中发生了什么呢?要回答这个问题,我们必须考虑一下代码中实际发生了什么。
在时间循环的每一次迭代中,我们使用当前时刻的波的数据来估计下一个时刻中的波的速度。最初,网格点数的增加返回了更准确的答案。数值扩散较少,波形看起来比第一个例子更像方波。
在每个时间步长内,波的传播距离大于网格尺寸dx。网格尺寸dx与总网格数量nx有关。因此,稳定计算条件需要满足下式:
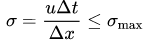
这里u为波速,σ常称之为Courant数,其值决定了计算是否稳定。在在新版本的代码中,我们采用CFL数来根据dx来计算合适的dt。
童鞋们尝试着增大时间步长试试,看看会发生什么情况。
下面改写代码:
#新代码
import numpy as np
import matplotlib.pyplot as plt
def linearconv_m(nx):
dx = 2 / ( nx - 1 )
nt = 20
c = 1
sigma = 0.5
dt = sigma * dx
u = np.ones(nx)
u[int(0.5 / dx):int(1 / dx + 1)] = 2
plt.plot(np.linspace(0,2,nx),u,'b',lw=3,label='origin')
un = np.ones(nx)
for n in range(nt):
un = u.copy()
for i in range(1,nx):
u[i] = un[i]- c* dt / dx * (un[i] - un[i-1])
plt.plot(np.linspace(0,2,nx),u,'r',lw=3,label='current')
plt.legend()测试一下新的程序代码:
linearconv_m(90)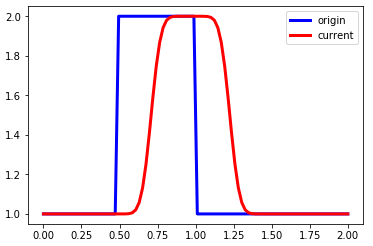
linearconv_m(180)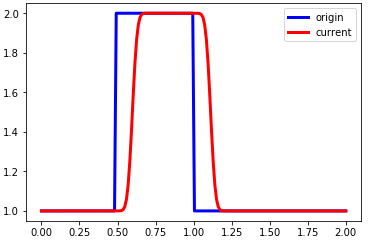
嗯,满足了CFL条件后,不管网格怎么加密,计算结果依然不会崩溃。

本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册