一维常系数对流方程是CFD中最简单最基本的方程。然而这个简单的方程能够告诉我们很多关于CFD方面的东西。模型方程如下式:

下面在Python中实现该求解过程。
代码如下所示:
import numpy as np
import matplotlib.pyplot as plt
nx = 41 #x方向网格节点数量
dx = 2/(nx-1) #空间网格步长,x方向总长度2
nt = 25 # 时间步数
dt = 0.025 # 时间步长
c = 1 #常数
# 指定初始条件
u = np.ones(nx)
u[int(0.5/dx):int(1/dx + 1)] = 2 #这一行实际上是制造了一个方波
# 下面将初始条件画出来
plt.plot(np.linspace(0,2,nx),u, 'r',lw=3, label = 'init')
# 计算25个时间步后的波形
un = np.ones(nx)
for n in range(nt):
un = u.copy() #后面的计算会改变u,所以将u拷贝一份
for i in range(1,nx):
u[i] = un[i] - c * dt / dx * (un[i] - un[i-1])
plt.plot(np.linspace(0,2,nx), u , 'b',lw =3,label= 'current')
plt.legend()计算结果如下图所示:
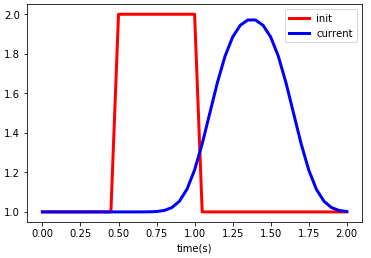
从图中可以看出,在经过大约0.625s后,波形存在一定程度上的失真,说明数值算法存在扩散。
注意:线性对流问题看似很简单,但实际上存在很多的问题,有兴趣的童鞋可以尝试着增大网格数量nx或增大时间步长dt,看看会发生什么情况,后面我们会专门讨论这个问题。

本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册