【Fluent热分析】02：自然对流

本案例演示利用Fluent求解计算自然对流问题。

案例模型来自于Star CCM+实例文档。

两个无限长同心圆柱体，其中小圆柱半径1.78 cm，壁面温度306.3 K，大圆柱半径1.628 cm，壁面温度293.7 K，计算由于壁面温度差异引起两圆柱间的环形空间内自然对流情况。几何模型尺寸如图所示。

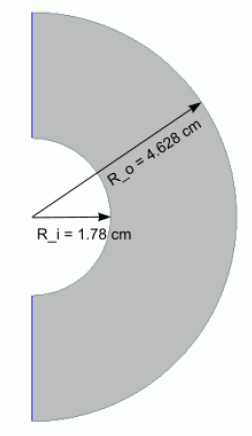
本案例采用2D模型进行计算，考虑几何与流场的对称性，采用1/2模型进行计算。

计算域中介质材料为空气，其物理属性如表所示。

案例参数基于实验数据，相应的瑞利数约为2.66E-4。

本案例模型在DM中进行创建。

• 启动Workbench，添加模块Fluid Flow(fluent)

• 右键选择A2单元格，点击弹出菜单项New DesignModeler Geometry…进入DM模块

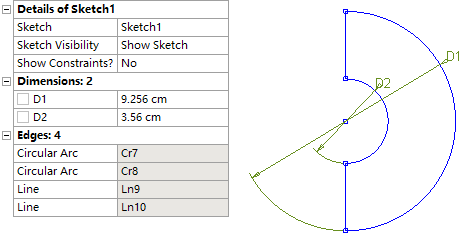
• 在XYPlane上创建如下图所示草图

• 选择菜单Concept → Surface from Sketches，属性窗口中设置Base Objects为前一步创建的草图，点击工具栏按钮Generate生成几何

• 关闭DM模块，返回至Workbench工作界面

• 双击A3单元格进入Mesh模块

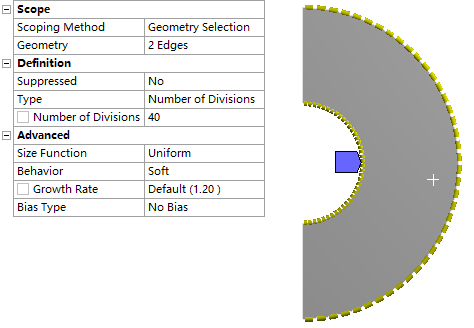
• 右键选择模型树节点Mesh，点击弹出菜单Insert → Sizing，属性窗口中设置Geometry为如图所示的两条半圆弧，设置Type为Number of Divisions，并设置其参数值为40

• 右键选择模型树节点Mesh，点击弹出菜单Insert → Sizing，属性窗口中设置Geometry为如图所示的两条直边，设置Type为Number of Divisions，并设置其参数值为40，设置Bias Type，并设置Bias Factor参数值为10

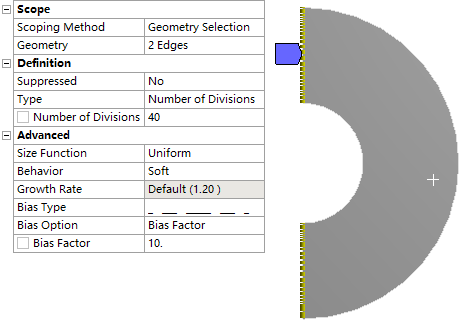
• 右键选择模型树节点Mesh，点击弹出菜单Insert → Face Meshing，属性窗口中设置Geometry为几何面

• 右键选择模型树节点Mesh，选择Generate Mesh生成网格

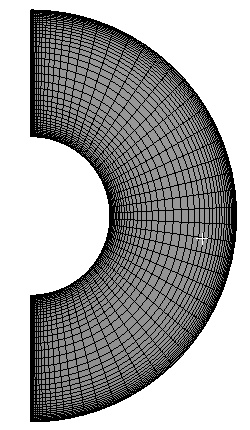
• 边界命名，如下图所示

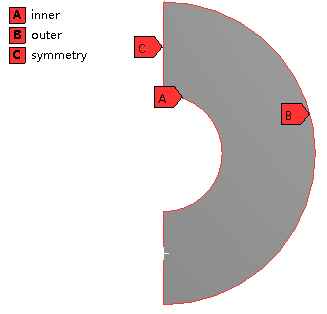
• 鼠标选中模型树节点Mesh，点击工具栏按钮Update更新网格

• 关闭Mesh模块，返回至Workbench工作界面

• 双击A4单元格启动Fluent模块，启动界面中激活选项Double Precision

• 双击模型树节点General，右侧面板中激活选项Gravity

• 设置重力加速度为(0 -9.81)

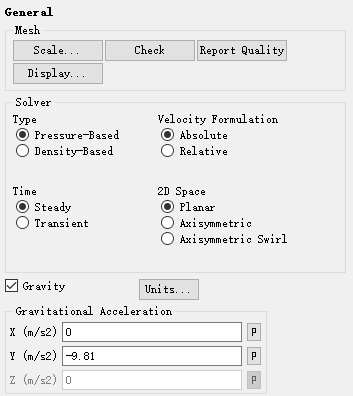
• 右键选择模型树节点Models > Energy，选择菜单On激活能量方程

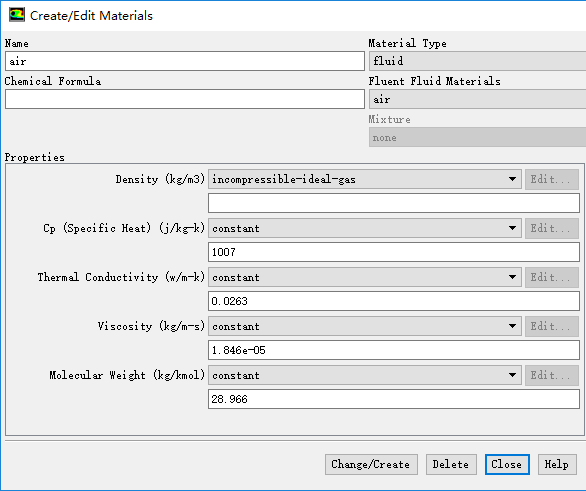
• 鼠标双击模型树节点Materials > fluid > air，弹出材料设置对话框，按下图所示进行参数设置

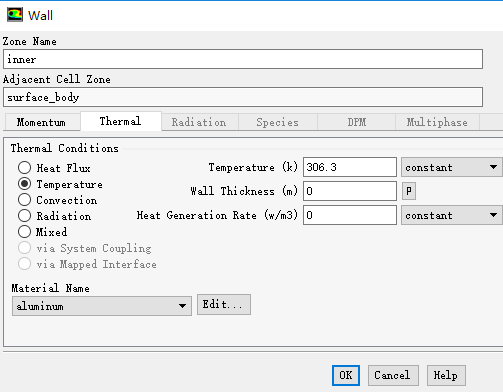
• 鼠标双击模型树节点Boundary Conditions > inner，弹出边界设置对话框

• 切换至Thermal标签页，激活选项Temperature，设置温度为306.3 K

• 点击OK按钮关闭对话框

• 相同方式设置outer边界，设置其温度为293.7 K

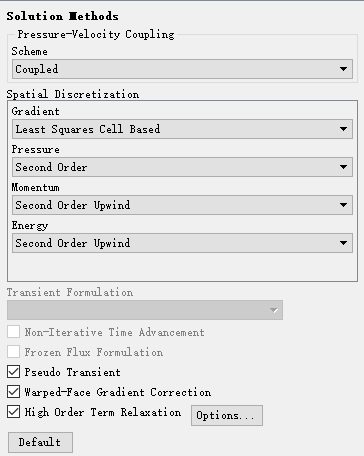
• 鼠标双击模型树节点Solution > Methods，右侧面板中设置Scheme为Coupled

• 激活选项Pseudo Transient

• 右键选择模型树节点Initialization，点击弹出菜单项Initialize进行初始化

• 鼠标双击模型树节点Run Calculation，右侧面板设置Number of Iterations为500，点击按钮Calculate进行计算

• 计算结束后关闭Fluent返回至Workbench工作窗口

• 鼠标双击A6单元格进入CFD-Post模块

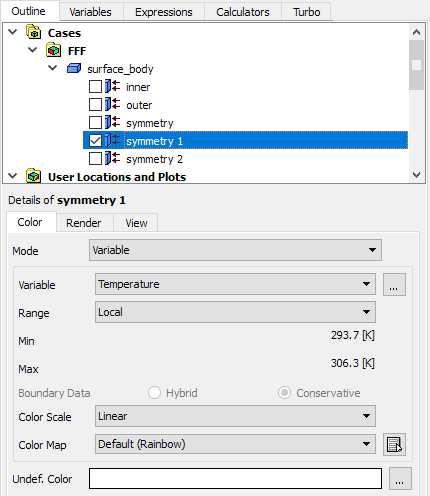
• 鼠标双击模型树节点symmetry 1，下方属性窗口中设置Mode为Variable，设置Variable为Temperature，设置Range为Local

• 点击下方的Apply按钮显示温度分布

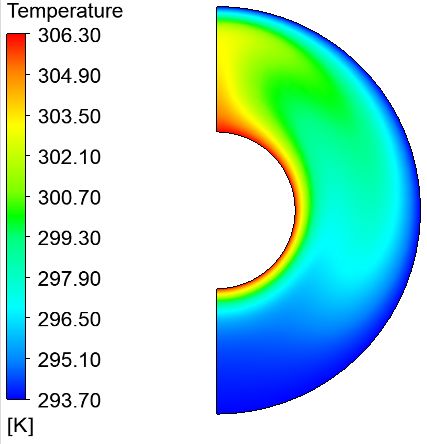
温度分布如图所示。

计算自然对流过程中的平衡导热率。Kuehn and Goldstein利用实验方式测量了本案例模型的平衡热导率(equivalentconductivity) 。平衡热导率定义为实际传热量与单纯到热量的比值：

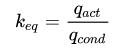
对于同心圆柱体： 

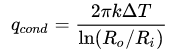
代入计算参数，可得qcond=2.177W/m

计算qact可以通过表达式计算：

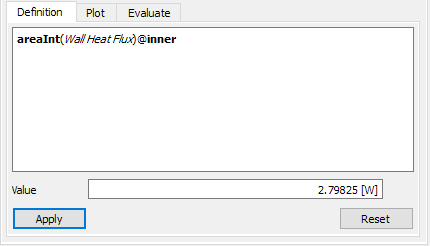
由于是半模型，因此qact=2.79825×2=5.5965w

代入上式可得：

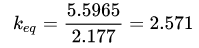
与实验值相吻合。

参考文献： Kuehn, T. H and Goldstein, R. J. An experimental study of natural convection heat transfer in concentric and eccentric horizontal cylindrical annuli. J. Heat Trans. (100) pp. 635-640, 1978.

本篇文章来源于微信公众号: CFD之道