最近AI大模型用得比较多(翻译和编程),然后就满世界的找便宜API用。好用的模型要么贵得离谱,要么充值麻烦,要么不仅贵得离谱还充值麻烦。国内的模型做翻译和润色其实挺不错的,不过在编程方面还存在一些差距。前阵子谷歌放出来的Gimini 2.0效果的确不错,在很大程度上可以平替Claude Sonnet,但是在国内没法直接使用,而且还不确定能免费使用多久。
这种问题其实早就存在,而且国内有不少做大模型中转的网站。但是很多都是一锤子买卖,很多充了米之后隔两天网站就打不开了。不过我前两天找到了一个国内的大模型API中转网站(网址:https://xiaohumini.site/register?aff=WE83),体验了一波感觉效果还不错。市面上的主流大模型基本都有,而且价格还比较划算。
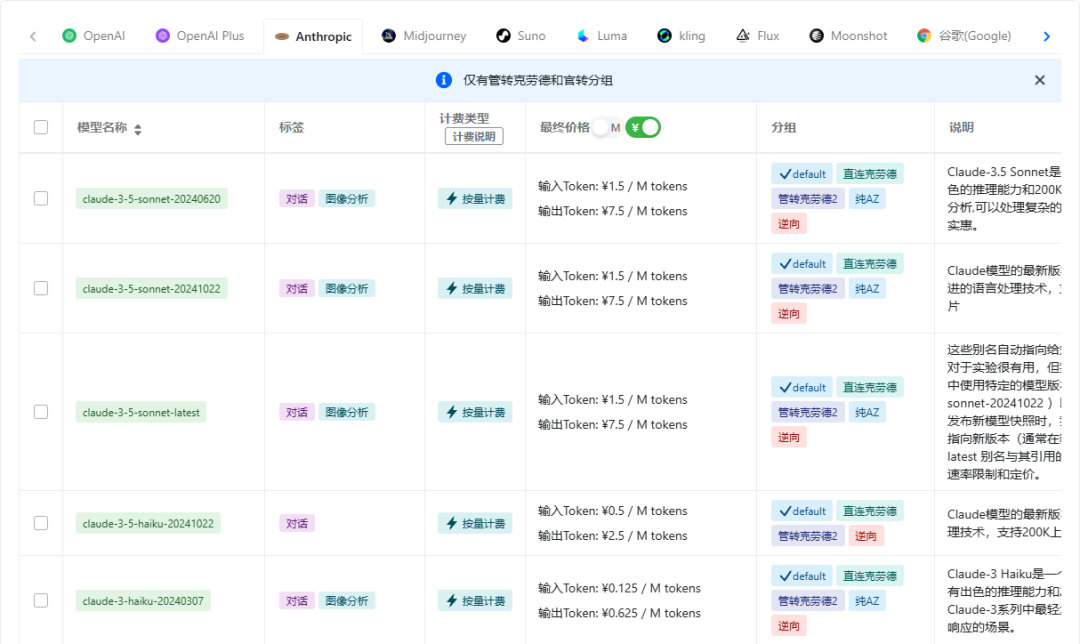
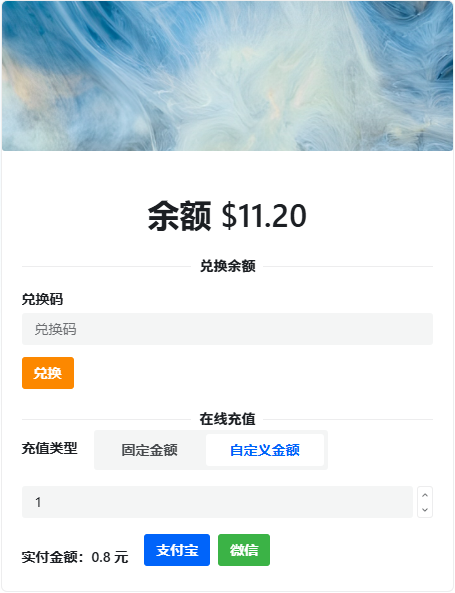
目前充值$1刀只需要¥0.8。
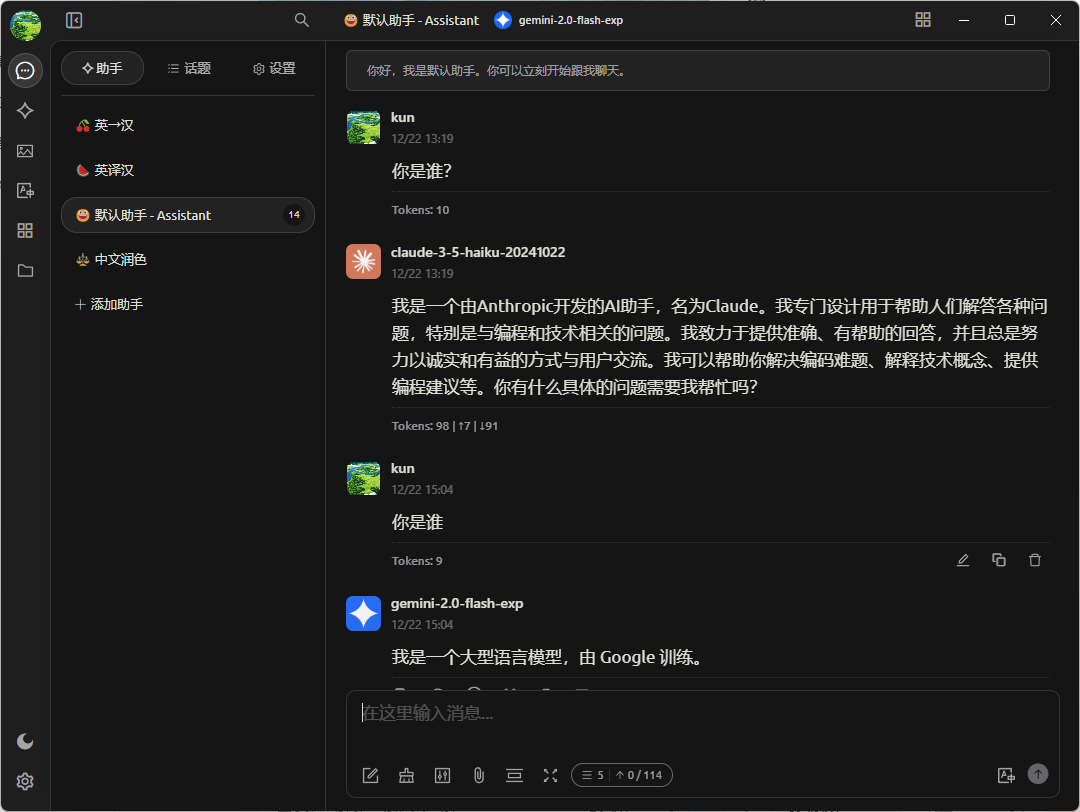
随便试了一下,响应速度还是挺快的 。
这个网站的API兼容OpenAI,配置起来非常简单。
先从网站搞到API Key。
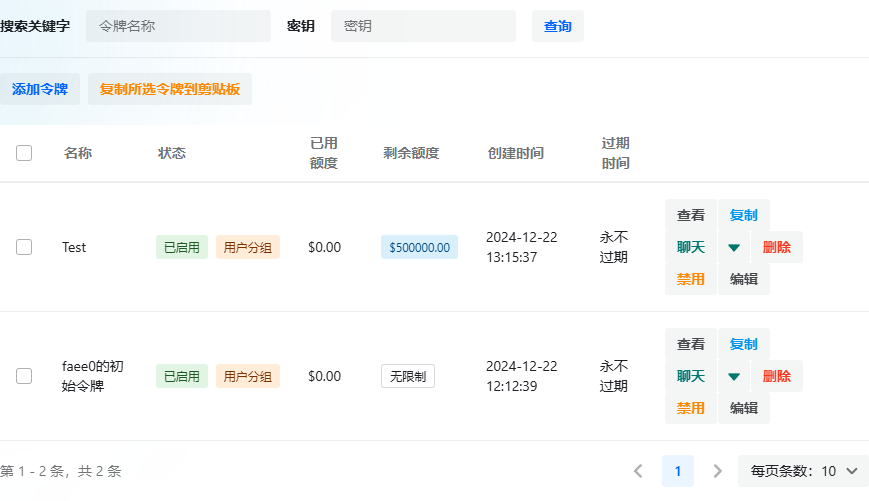
然后随便找个前端软件简单配置就可以了。如下面是在Cherry Studio中配置。
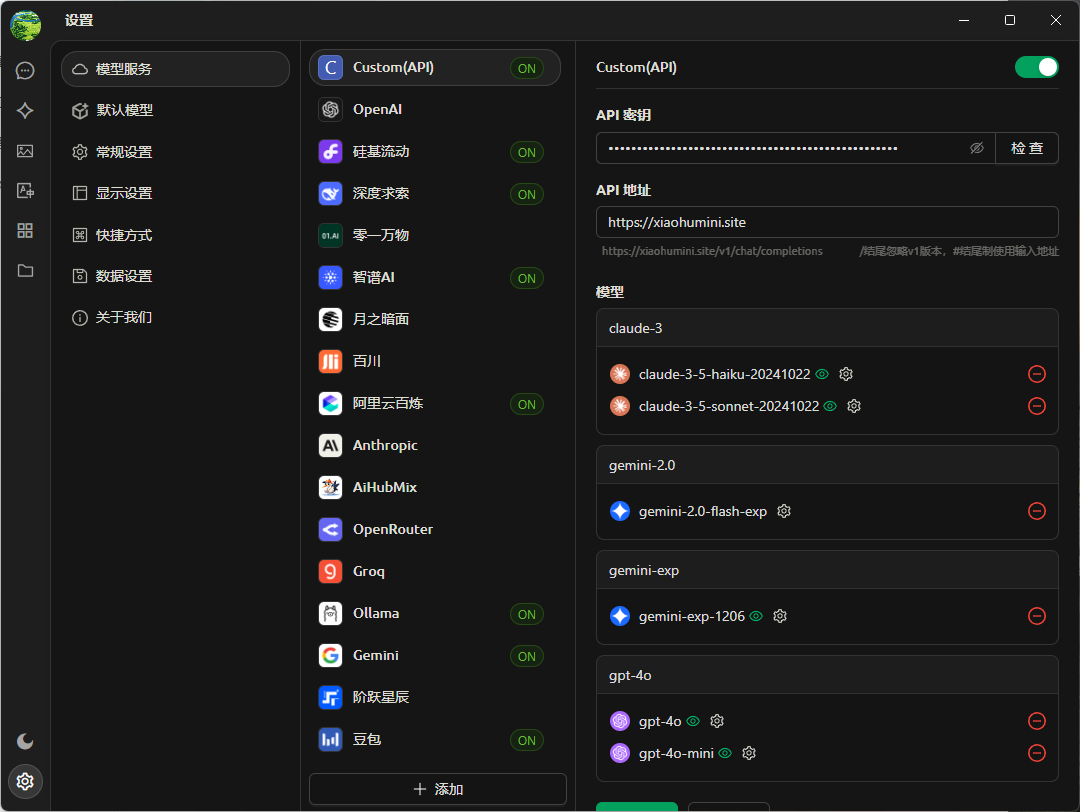
有想要体验的道友可以尝试(网址:https://xiaohumini.site/register?aff=WE83),不过还是提醒一下,用多少充多少(我每次最多充10块钱),以防哪天就倒闭了。就像去理发店剪头一样,不要随便充大几百,转过身店子换成了奶茶店,哭都找不到地方哭。
(完)
本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册