Bénard 是第一位通过实验研究底部加热的自由表面流体层中对流现象的科学家。Rayleigh 运用线性稳定性分析，从理论上解释并深入探讨了底部较热的水平平行板之间流体运动的稳定性。Chandrasekhar 完成了 Rayleigh-Bénard 对流的线性稳定性分析，而 Koschmieder 则展示了此后几十年该领域研究的显著进展。

在Rayleigh-Bénard对流研究领域，仅有少数实验成功地生成了符合稳定性理论预测的同心环状单元结构。这些实验包括Koschmieder和Pallas、Hoard等人以及Matsson的研究。根据该理论，这种结构应在具有刚性上边界条件下出现。然而，实验表明，上部刚性壁面的不稳定性对表面粗糙度和平整度极为敏感。Torres等人通过圆柱形容器内Rayleigh-Benard对流的3D数值模拟，进一步验证了以同心圆形式存在的滚筒单元的存在。本案例深入研究Rayleigh-Bénard对流问题，并采用Fluent进行三维分析。

1 问题描述

计算模型如下图所示，密闭的圆柱形容器内充满水，其中顶部壁面（冷壁面）温度为296.5 K，底部壁面（热壁面）温度为298 K，容器直径100 mm，高度 4.8 mm。

2 Fluent设置

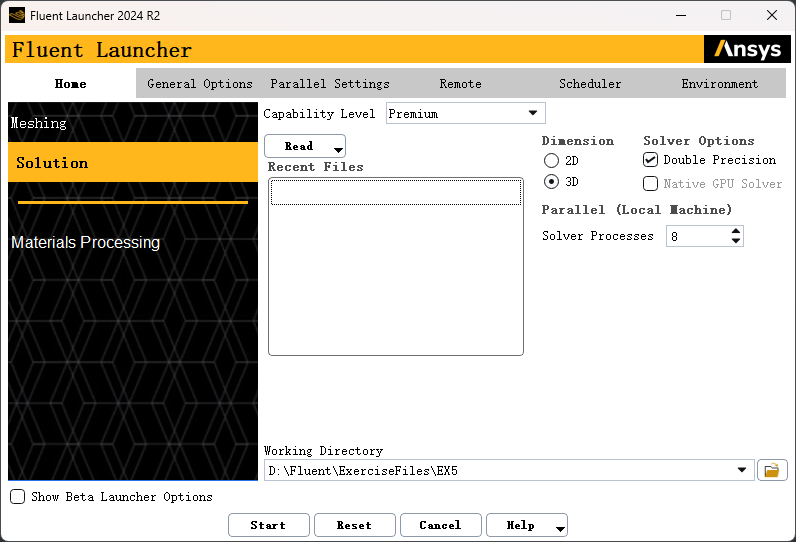
• 以 3D、Double Precision 方式启动Fluent

• 利用菜单 File → Read→ Mesh… 读取网格文件 rayleigh-benard-3D.msh

2.1 General设置

• 进入General任务页，如下图所示，设置重力加速度为[0 0 -9.81]

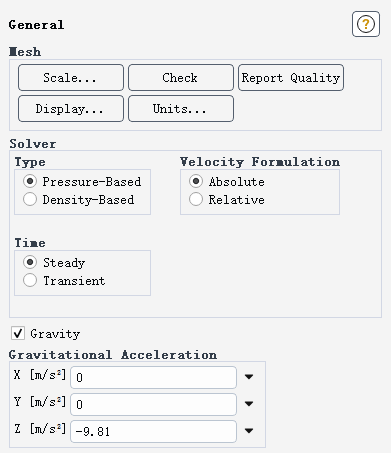
2.2 Models设置

• 双击模型树节点 Models → Energy ，在打开的对话框中激活 Energy Equation

• 右键选择模型树节点 Models → Viscous ，选择菜单项 Model → Liminar ，如下图所示

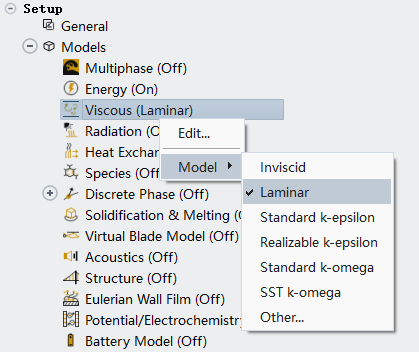
2.3 Materials设置

• 从材料库中加载water-liquid

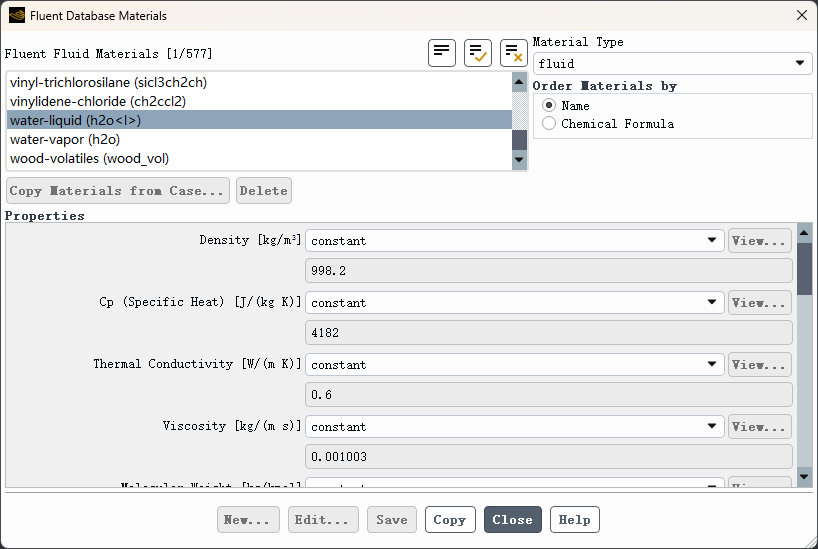
• 修改water-liquid的材料参数，如下图所示
• 指定Density为 boussinesq ，并指定密度值为 997 kg/m3
• 指定参数Thermal Expansion Coefficient为 0.000247

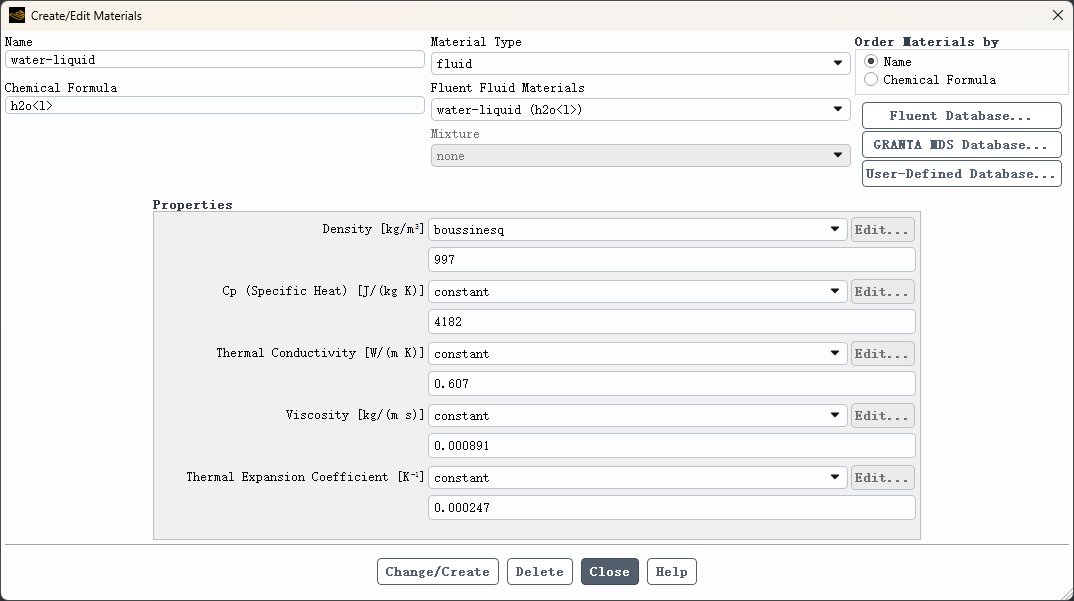
2.4 计算区域设置

• 设置计算区域的材料介质为water-liquid，如下图所示

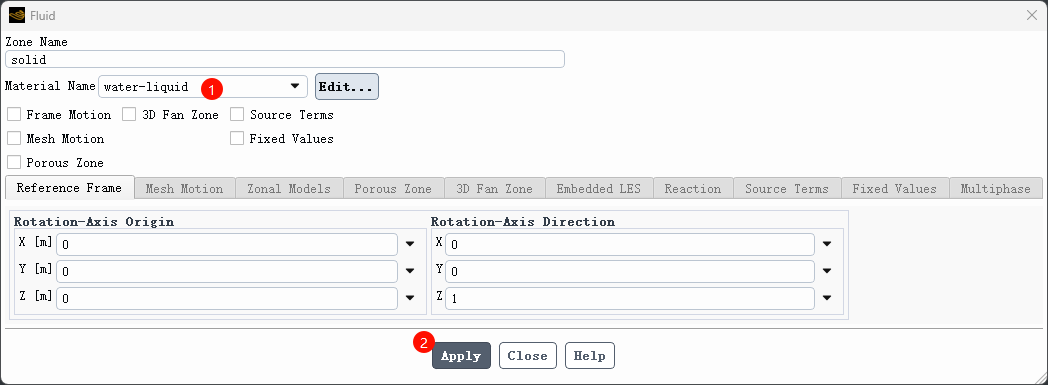
2.5 边界条件设置

1、cold_wall边界

• 双击模型树节点Boundary Conditions → cold_wall打开边界条件设置对话框，进入 Thermal 选项卡，指定Thermal Conditions为 Temperature ，并指定温度为 296.79 K

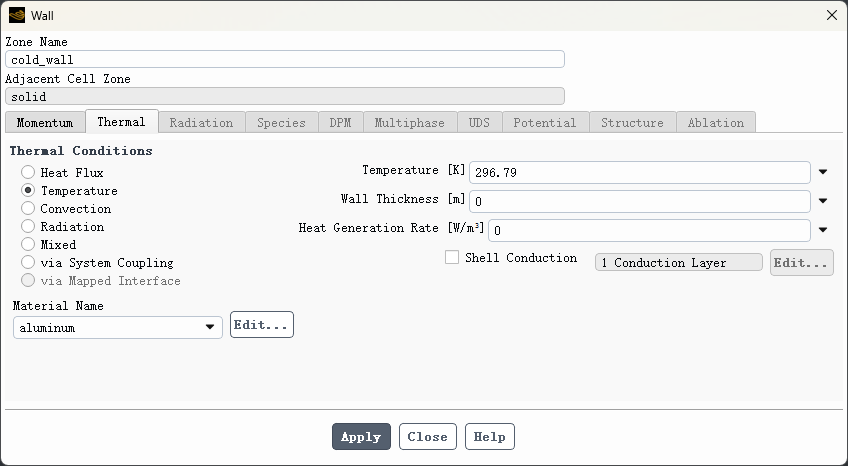
2、hot_wall边界

• 相同方式指定hot_wall边界温度值为 298 K，如下图所示

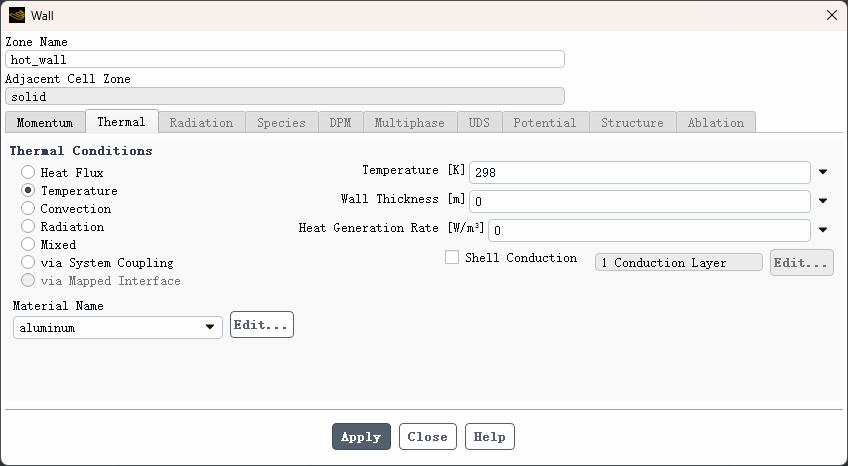
3、side_wall

• 如下图所示，指定边界side_wall的温度值为 296.79 K

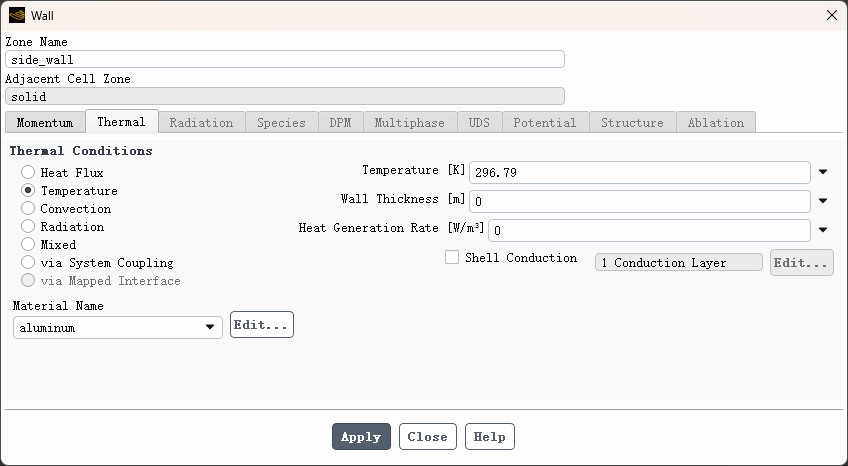
2.6 Methods设置

• 双击模型树节点Methods，如下图所示设置计算方法

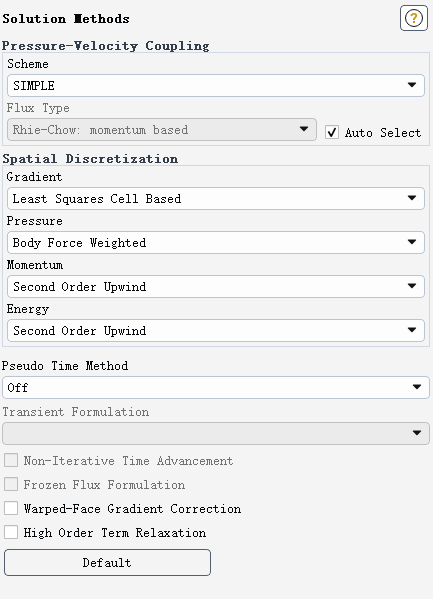
2.7 初始化计算

• 双击模型树节点Initialization打开初始化任务页，如下图所示设置初始值并点击按钮 Initialize 进行初始化

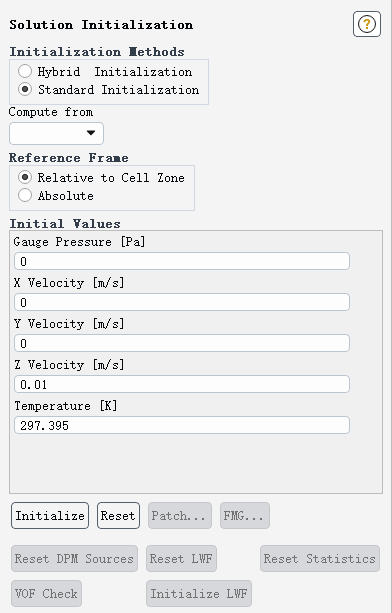
2.8 残差标准

• 双击模型树节点Monitor → Residual打开残差监视器对话框，如下图所示设置方程的残差标准

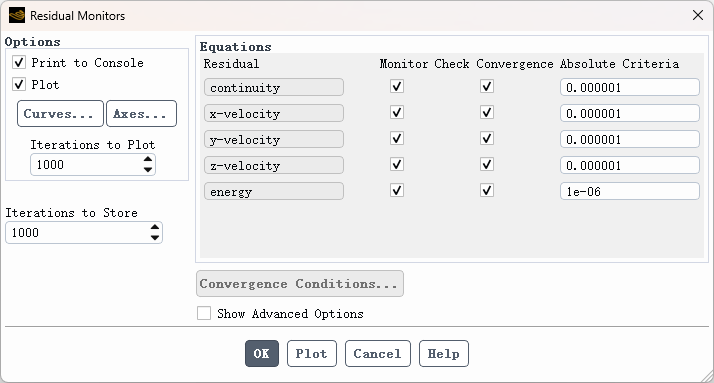
2.9 设置操作条件

• 点击工作区按钮Physics > Operating Conditions...打开操作条件对话框，如下图所示指定操作参数

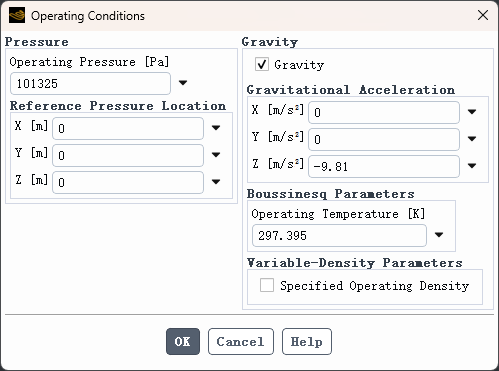
2.10 进行计算

• 双击模型树节点Run Calculation进入求解计算任务页，如下图所示设置迭代计算 3500 步，点击按钮 Calculate 开始计算

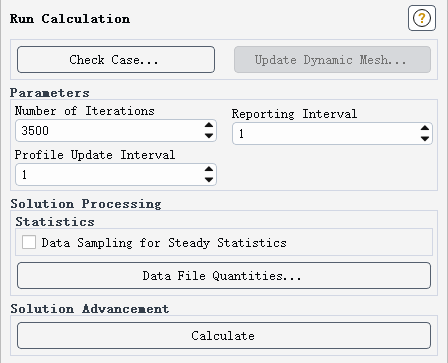
计算残差变化如图所示。

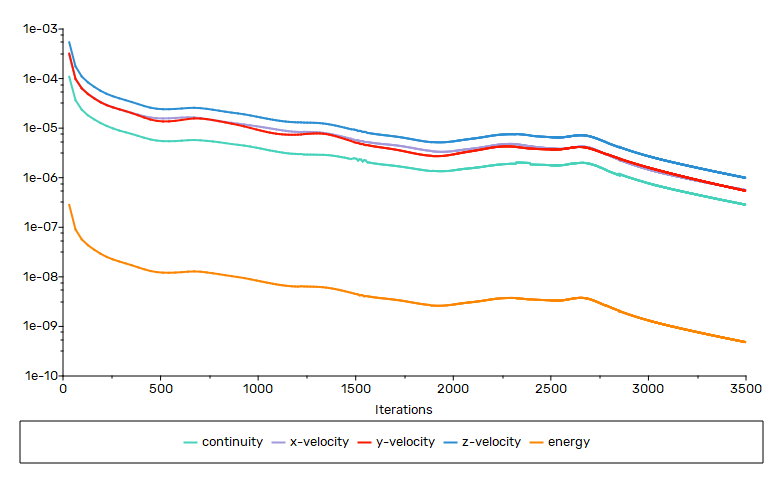
注：确保计算残差收敛。

”

3 查看结果

• 右键选择模型树节点 Results → Surface ，点击弹出菜单项 New → Plane… 打开平面创建对话框

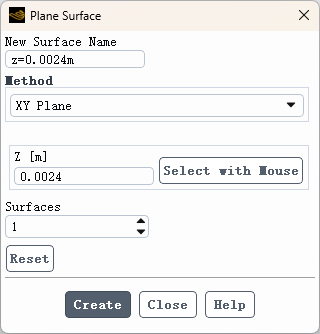
• 如下图所示创建z=0.0024 m的XY平面

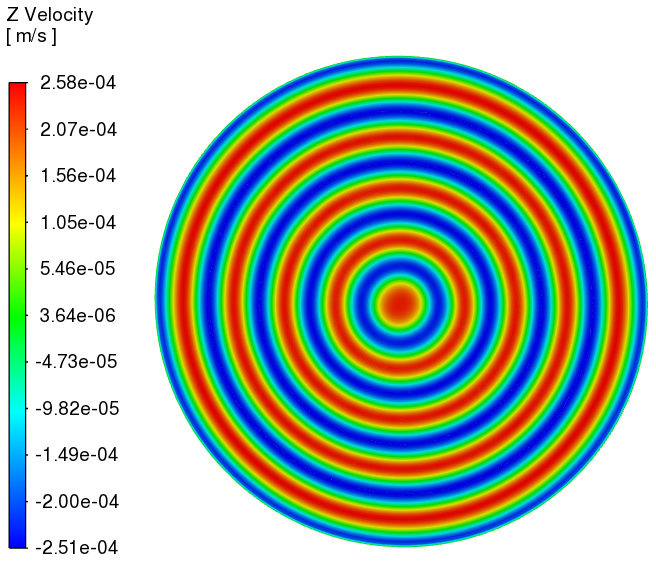
• XY平面（z=0.0024m）上Z方向速度分布

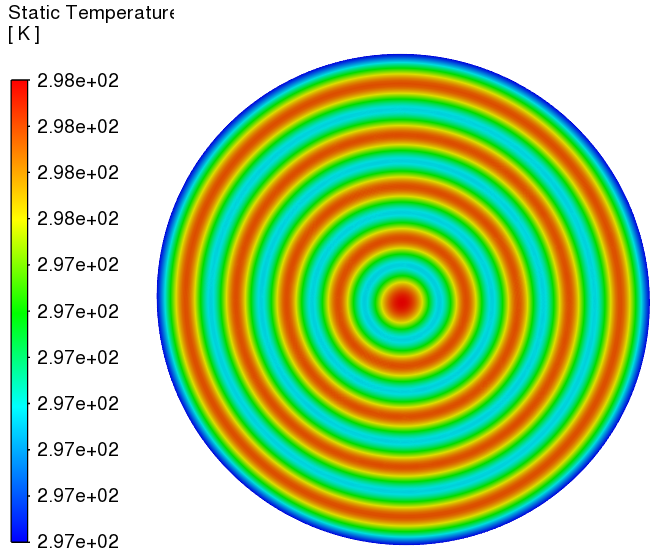
• XY平面（z=0.0024m）上温度分布

• YZ面上的Z Velocity分布

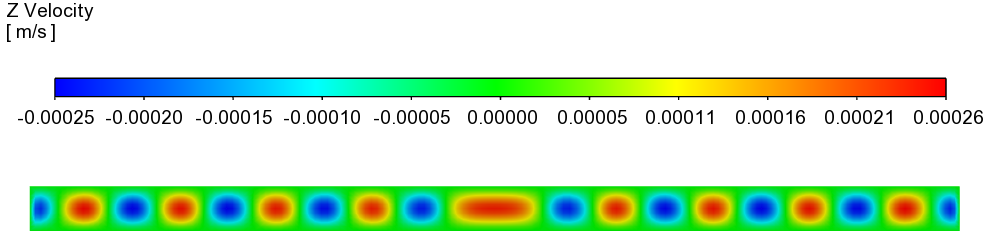
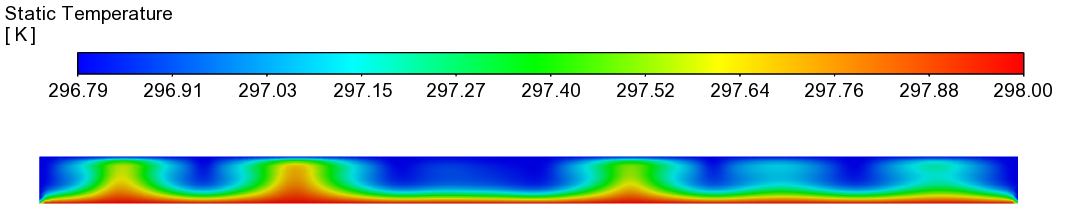
• YZ面上温度分布

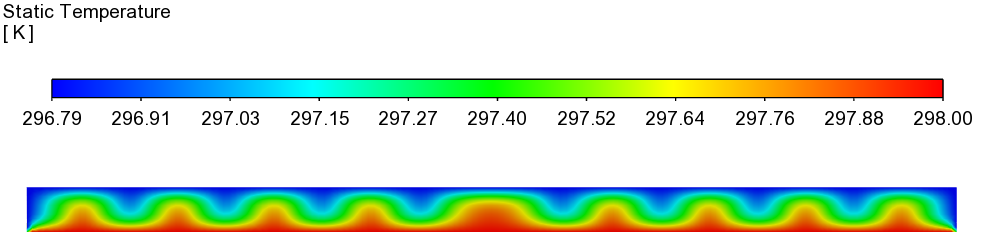
4 修改边界

Rayleigh-Bénard对流结果依赖于上下壁面边界条件。这里修改冷壁面的边界条件，看看计算结果会有哪些变化。

• 打开cold_wall边界条件设置对话框，如下图所示，指定Shear Conditions为 Marangoni stress ，指定 Surface Tension Gradient为 -2e-5

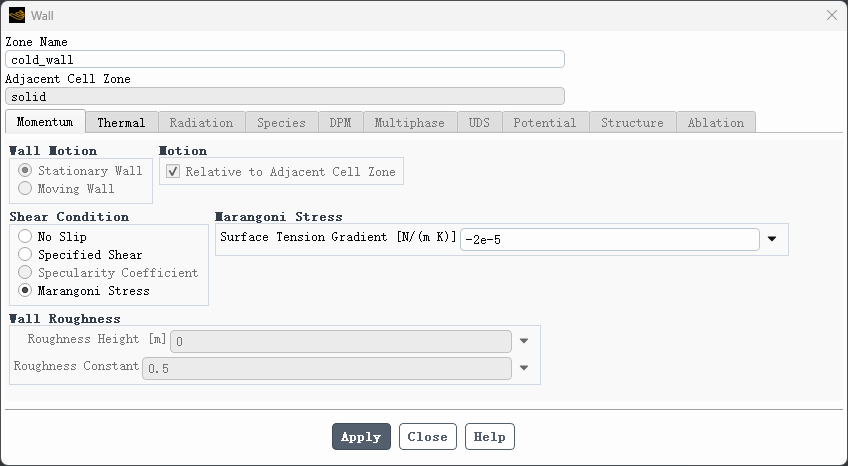
• 进行初始化计算

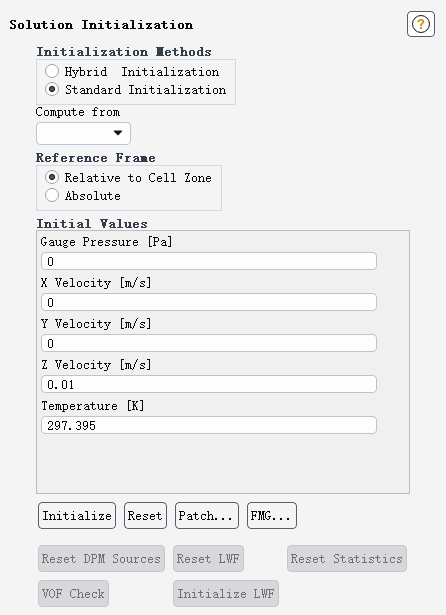
• 进行求解计算

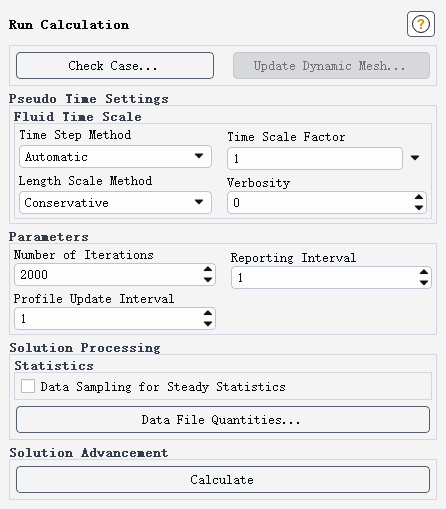
• XY平面（z=0.0024 m）z velocity分布

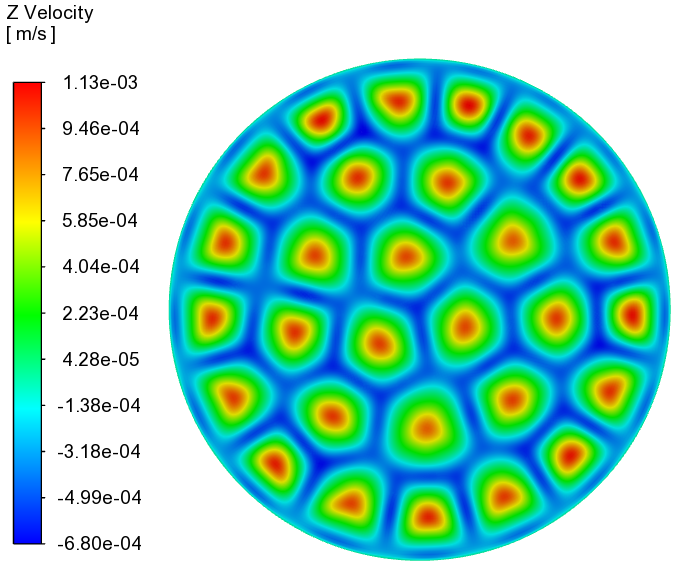
• XY平面上（z=0.0024 m）温度分布

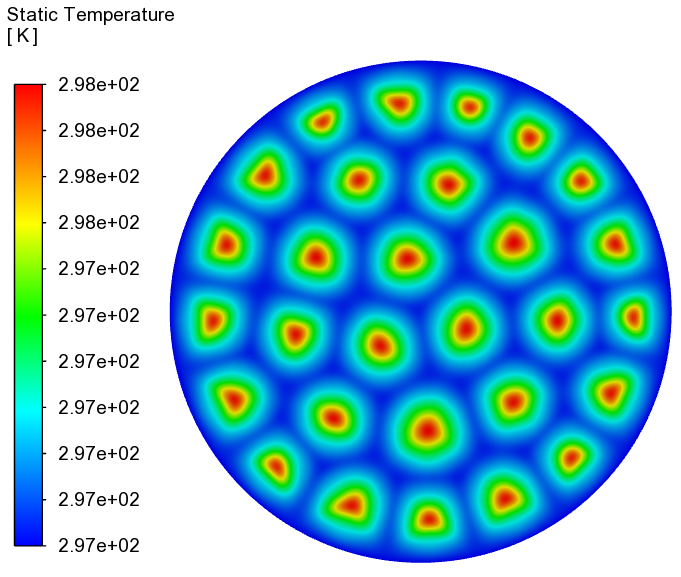
• YZ平面上速度

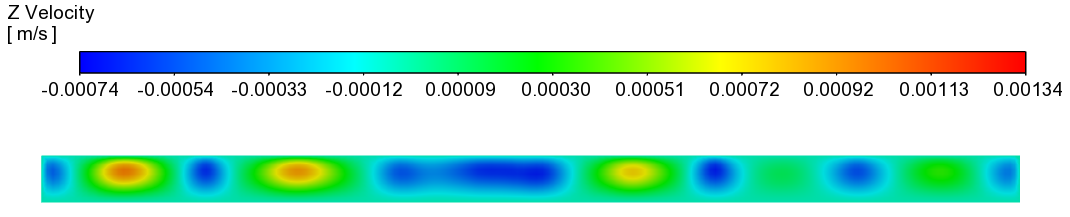
• YZ平面上温度分布

（完）