在Fluent中使用多孔介质区域或多孔阶跃边界时,需要对实验数据进行拟合。
在应用这类条件时,往往需要进行大量的试验以获取压力降与速度之间的函数关系,再将函数表达式中的系数换算成软件中的输入参数。而在软件求解计算的过程中,软件会利用输入的参数还原压力降与速度之间的函数关系。
通常情况下,压降-速度之间的函数表达式为截距为零的二次多项式:
-
确保试验的速度范围完全涵盖仿真计算的速度范围。 -
函数拟合时确保系数和均为正值
| 速度(m/s) | 压力降(Pa) |
|---|---|
| 0 | 0 |
| 1 | 3851 |
| 2 | 15418 |
| 3 | 34413 |
| 4 | 62158 |
| 5 | 98711 |
直接采用最小二乘法进行二次多项式拟合(指定截距为零),拟合结果如下所示。
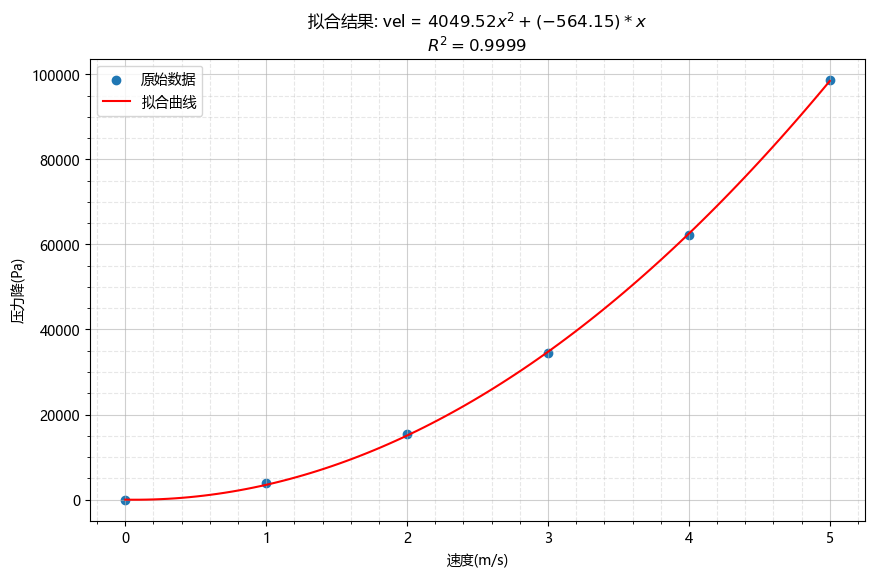
| 速度(m/s) | 压力降(Pa) |
|---|---|
| 0 | 0 |
| 0.9 | 3851 |
| 1.9 | 15418 |
| 2.9 | 34413 |
| 3.9 | 62158 |
| 4.9 | 98711 |
拟合后的结果为:
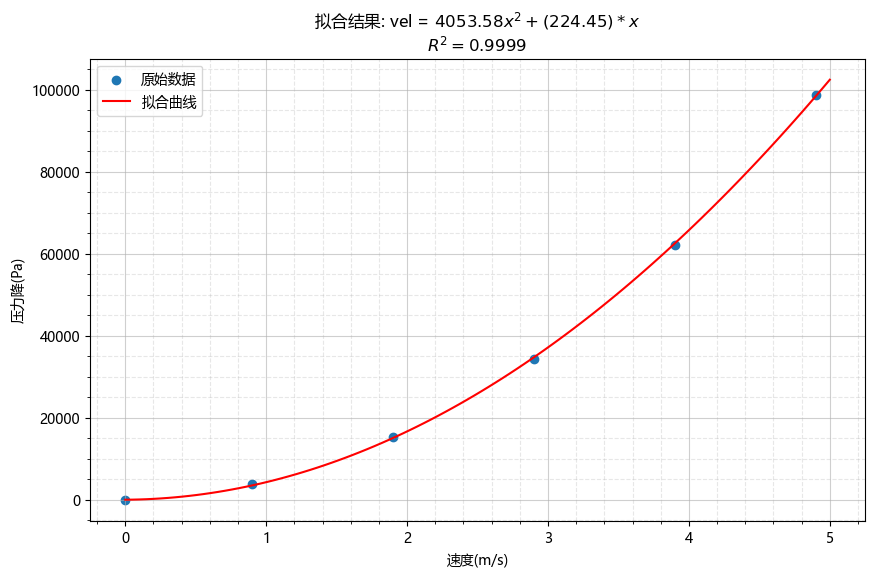
可以看到,两个系数均变为了正值。这种方法简单粗暴,但是修改数据总是令人觉得不安。
方式2:拟合时约束系数值大于0
在对数据进行拟合的过程中,强制约束系数值大于等于零。拟合结果如下图所示。
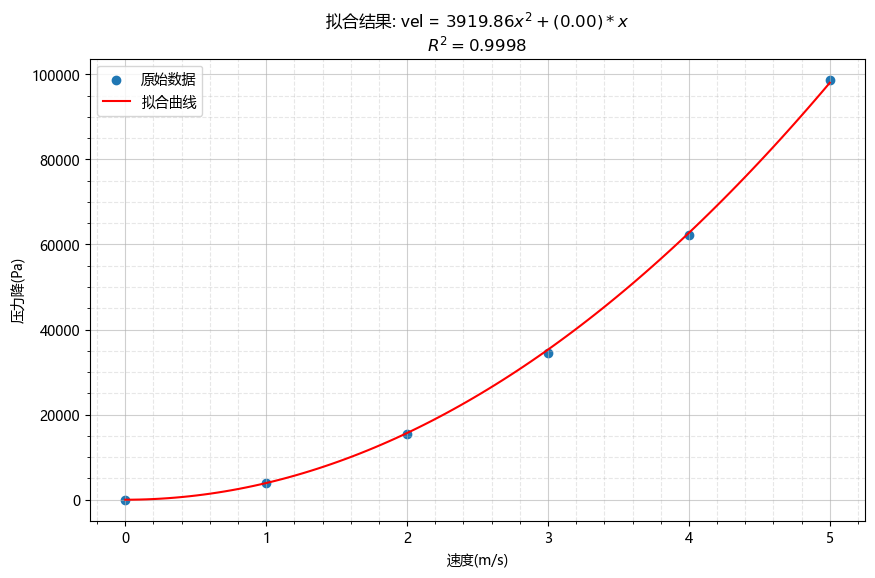
| 速度(m/s) | 压力降(Pa) | 直接拟合(Pa) | 方法1(Pa) | 方法2(Pa) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 1 | 3851 | 3485.37 | 4278.03 | 3919.86 |
| 2 | 15418 | 15069.78 | 16663.22 | 15679.44 |
| 3 | 34413 | 34753.23 | 37155.57 | 35278.74 |
| 4 | 62158 | 62535.72 | 65755.08 | 62717.76 |
| 5 | 98711 | 98417.25 | 102461.8 | 97996.5 |
三种方法和测试值比较的偏差如下表所示。
| 速度(m/s) | 压力降(Pa) | 直接拟合偏差(%) | 方法1偏差(%) | 方法2偏差(%) |
|---|---|---|---|---|
| 0 | 0 | 0.00% | 0.00% | 0.00% |
| 1 | 3851 | -9.49% | 11.09% | 1.79% |
| 2 | 15418 | -2.26% | 8.08% | 1.70% |
| 3 | 34413 | 0.99% | 7.97% | 2.52% |
| 4 | 62158 | 0.61% | 5.79% | 0.90% |
| 5 | 98711 | -0.30% | 3.80% | -0.72% |
可以看到方法2的处理方式是可行的。其拟合程序如下所示。
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['MicroSoft YaHei'] # 指定使用的中文字体
# 定义二次函数模型,确保截距为0
def quadratic_model(x, a, b):
return a * x**2 + b * x
# 读取数据(这里使用您提供的示例数据)
vel = np.array([0,1, 2, 3, 4, 5])
dp = np.array([0,3851, 15418, 34413, 62158, 98711])
# 进行曲线拟合,指定参数值的范围为大于1-e6
popt, pcov = curve_fit(quadratic_model, vel, dp, bounds=(1e-6, np.inf))
# 获取拟合参数
a, b = popt
# 计算R平方值
residuals = dp - quadratic_model(vel, a, b)
ss_res = np.sum(residuals**2)
ss_tot = np.sum((dp - np.mean(dp))**2)
r_squared = 1 - (ss_res / ss_tot)
# 打印拟合结果
print(f"拟合公式: velocity = {a:.2f} * x^2 + {b:.2f} * x")
print(f"R平方值: {r_squared:.4f}")
# 绘制原始数据和拟合曲线
plt.figure(figsize=(10, 6))
plt.scatter(vel, dp, label='原始数据')
x_fit = np.linspace(0, 5, 100)
y_fit = quadratic_model(x_fit, a, b)
plt.plot(x_fit, y_fit, 'r-', label='拟合曲线')
plt.xlabel('速度(m/s)')
plt.ylabel('压力降(Pa)')
plt.legend()
plt.title(f"拟合结果: vel = ${a:.2f} x^2 + ({b:.2f}) * x$n$R^2= {r_squared:.4f}$")
plt.grid()
plt.grid(which='major',alpha= 0.6)
plt.grid(which='minor', alpha=0.3,linestyle='--')
plt.minorticks_on()
plt.show()
(完)
本篇文章来源于微信公众号: CFD之道








评论前必须登录!
注册