本节展示使用曲率修正（见上文第 3.4.2 节）的两个示例：NACA-0012 翼尖涡流及水力旋流器中的流动。这两个示例中均将SST 模型与曲率修正（SST-CC）结合在一起使用。

1 NACA-0012翼尖涡旋

NACA 0012 翼尖涡流测试案例基于 Chow 等人的实验[44]。机翼下游位置有一些详细的实验数据，包括速度场、压力和雷诺应力。图 51 所示的三维机翼具有圆形翼尖，并被放置于风洞内。由于升力的作用，来自压力侧的气流绕着圆形翼尖流动，并在下游形成强烈的漩涡。基于弦长的雷诺数为Re = 460 万，马赫数约为 0.1，攻角 α = 10°。在实验中，机翼前缘的流动为完全湍流。

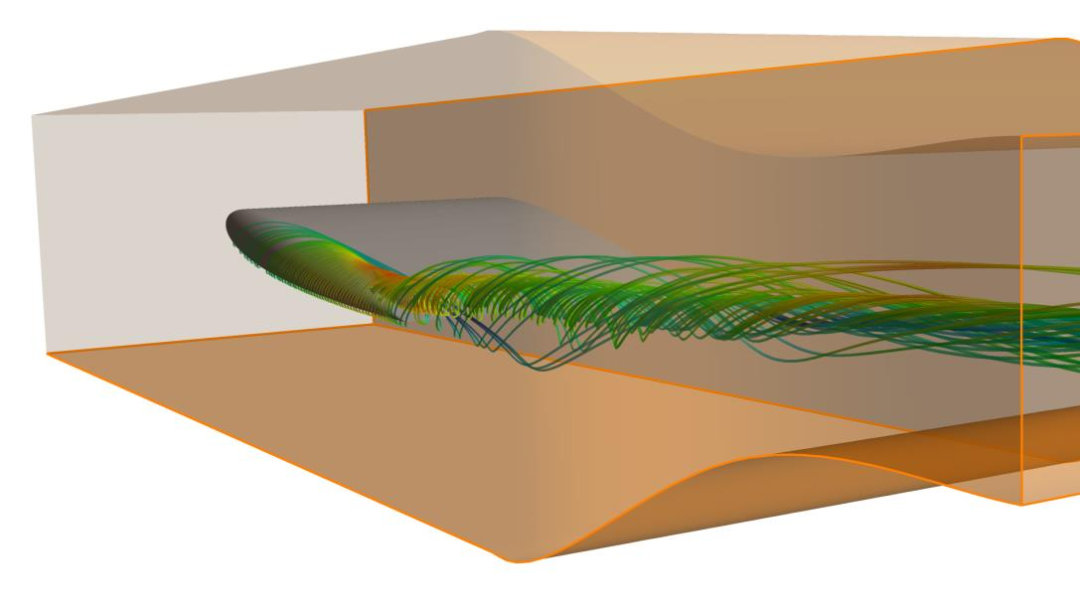
当前的模拟采用了以下边界条件：入口截面位置指定了一个高于大气压的总压 = 1760 Pa。入口的湍流特性根据湍流强度 = 0.15%和湍流粘度比等于TVR = 5计算得到。出口边界指定质量流率 = 67.25 [kg/s]。这使得入口平均速度= 51.81 [m/s]，其与实验值相匹配。不考虑风洞壁面上的边界层，在风洞壁面上指定了对称边界条件用于模拟滑移壁面，并在NACA-0012机翼上指定无滑移壁面条件。

图 52 显示了机翼后缘下游 X/C = 0.67 处的涡粘分布，从中可以看出曲率修正的机制。SST-CC 模型在涡核区域提供了较低的湍流粘度，这是由于 CC 修正减少了湍动能的产生，这防止了核心轴向速度过早衰减到远低于自由流的值。

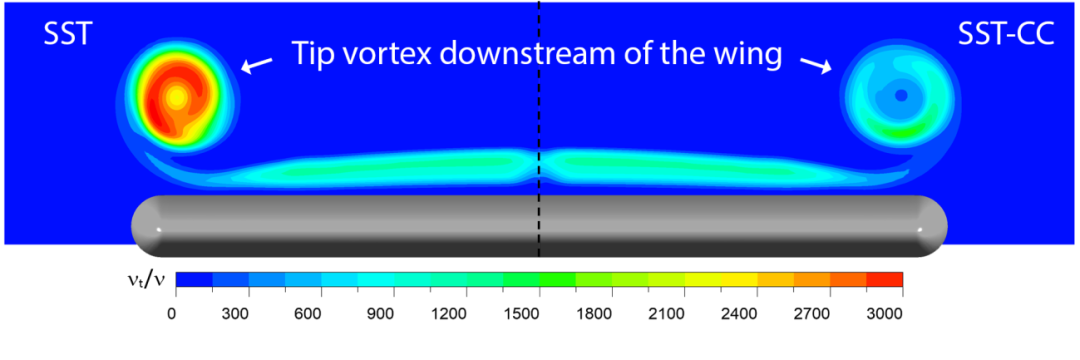
图 53 显示了位于后缘下游的三个平面上的非三维横流速度和轴向速度的预测值与实验数据的对比，图中坐标 X/C 基于与机翼后缘的距离。可以看出，SST-CC 模型能更好地捕捉涡强度，这是由流向速度的最大值测量的。从轴向速度图中也可以看出，原始 SST 模型的涡衰减过快。与 SST 相比，SST-CC 模型在 X/C = 0.24 处有明显改善。然而在最下游的 X/C = 0.67 处，尽管修正后涡粘度大大降低，但 SST-CC 模型也无法再现实验速度分布。然而，轴向自由流值也存在一些不匹配，这表明实验与 CFD 设置之间可能存在差异。

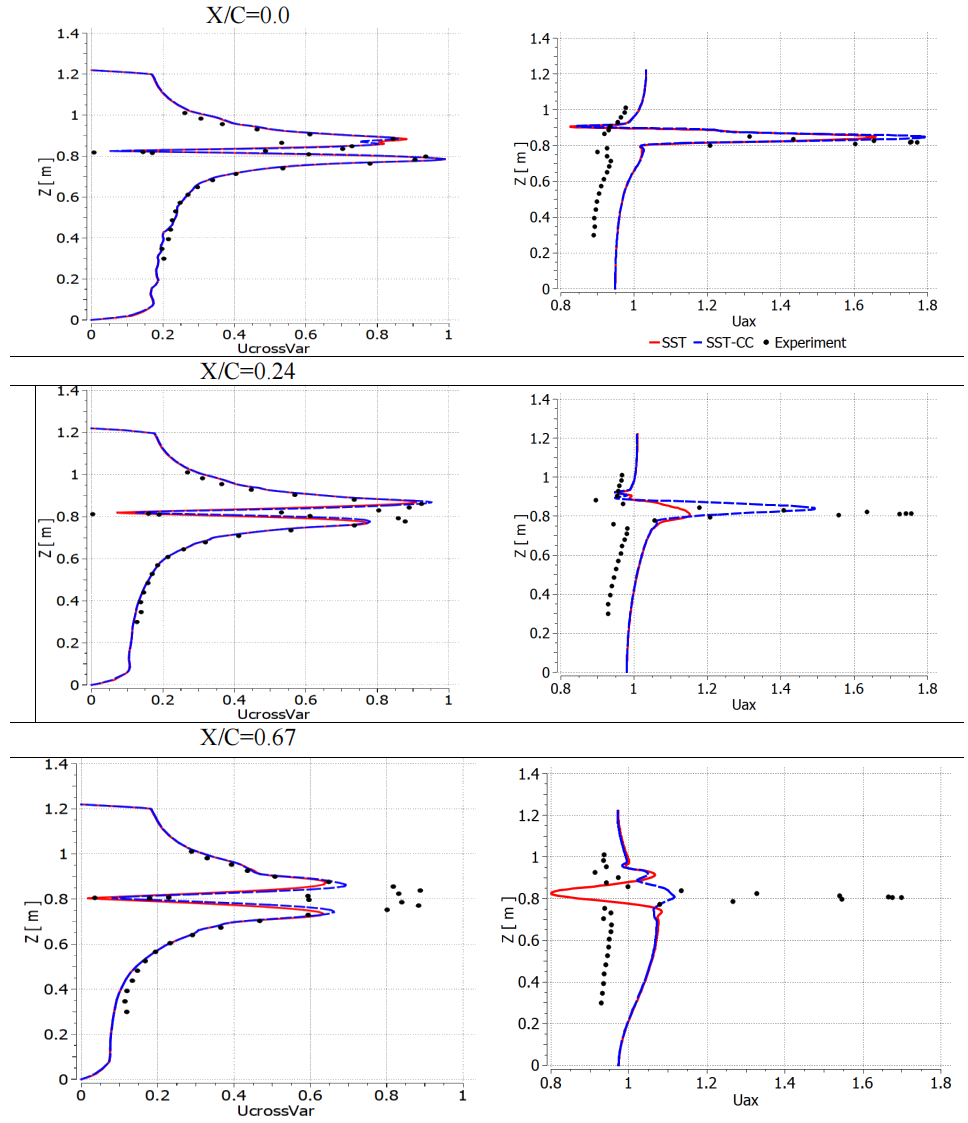
图 54 显示了曲率修正对穿过涡核的平面轴向速度的等值线图的影响。在使用曲率修正扩展时，流动加速度增加的区域清晰可见。不过在测量位置 X/C = 0.67 的上游，这种现象消失。

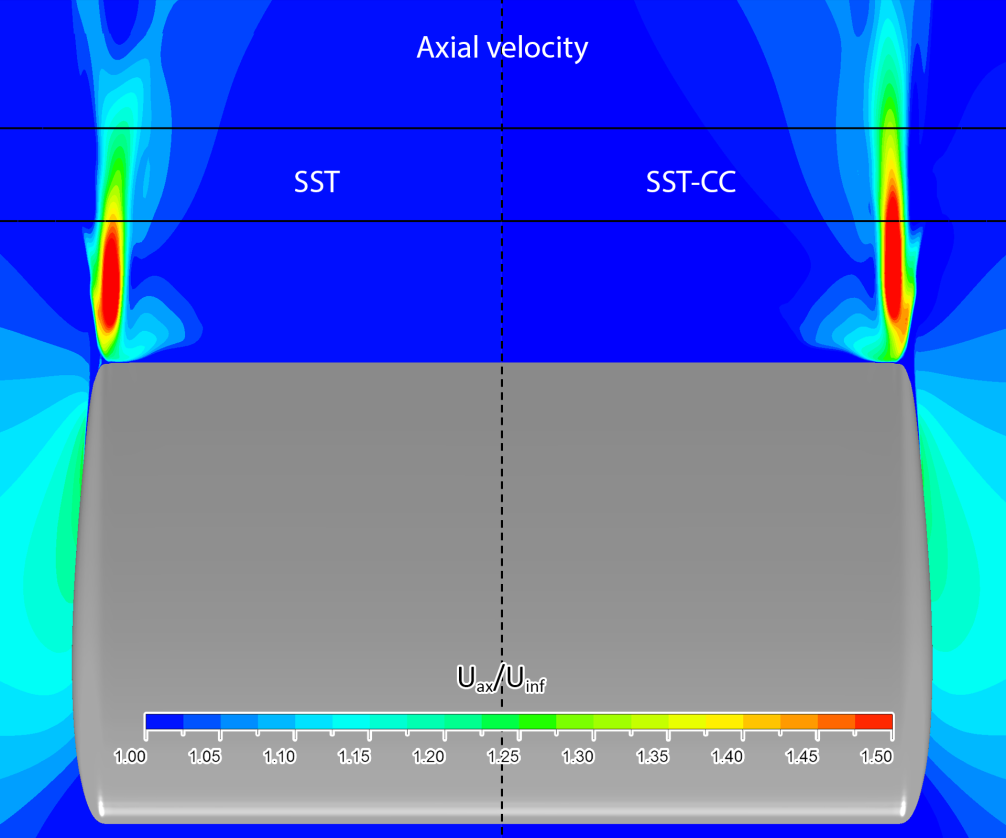
2 水力旋流器中的流动

水力旋流器的典型流动结构和几何形状如图 55 所示。旋流器利用强漩流中颗粒所受的强径向力实现分离。流体/颗粒混合物从切线方向注入旋流器，在旋流器筒体（圆柱形部分）中向下螺旋流动，然后进入旋流器锥形部分。在离心力的作用下，重颗粒被推向壁面，并在重力作用下从下部出口排出。轻颗粒则向旋流器轴线方向移动，在那里与中心涡流中的上行流汇合，从顶部出口离开旋流器。水力旋流器内部流动的特点是在中心区域形成一个强漩涡核心。要准确预测这种流动，正确表示湍流是湍流模型的一项极具挑战性的任务。

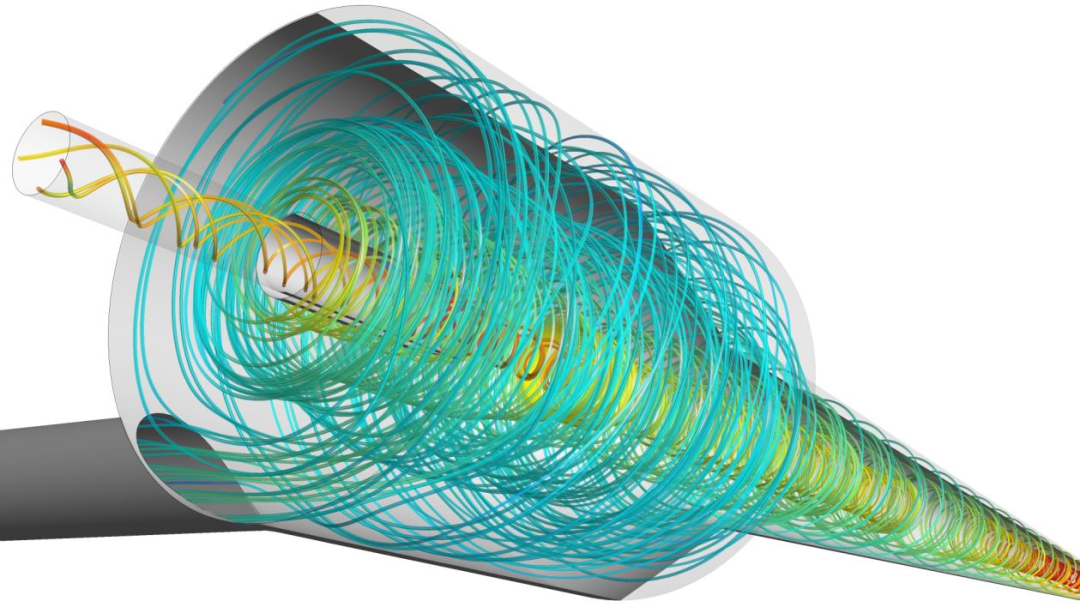
当前的模拟是针对Hartley实验研究的水力旋流器进行的。旋流器中不同垂直位置的轴向速度和切向速度的实验数据均可获得。需要注意的是，使用稳态方法，无法获得物理上正确的结果，因此必须在非稳态模式下运行。这在物理上是正确的，因为众所周知，涡旋核心是非稳态的，其会在旋流器的轴线周围蜿蜒流动。

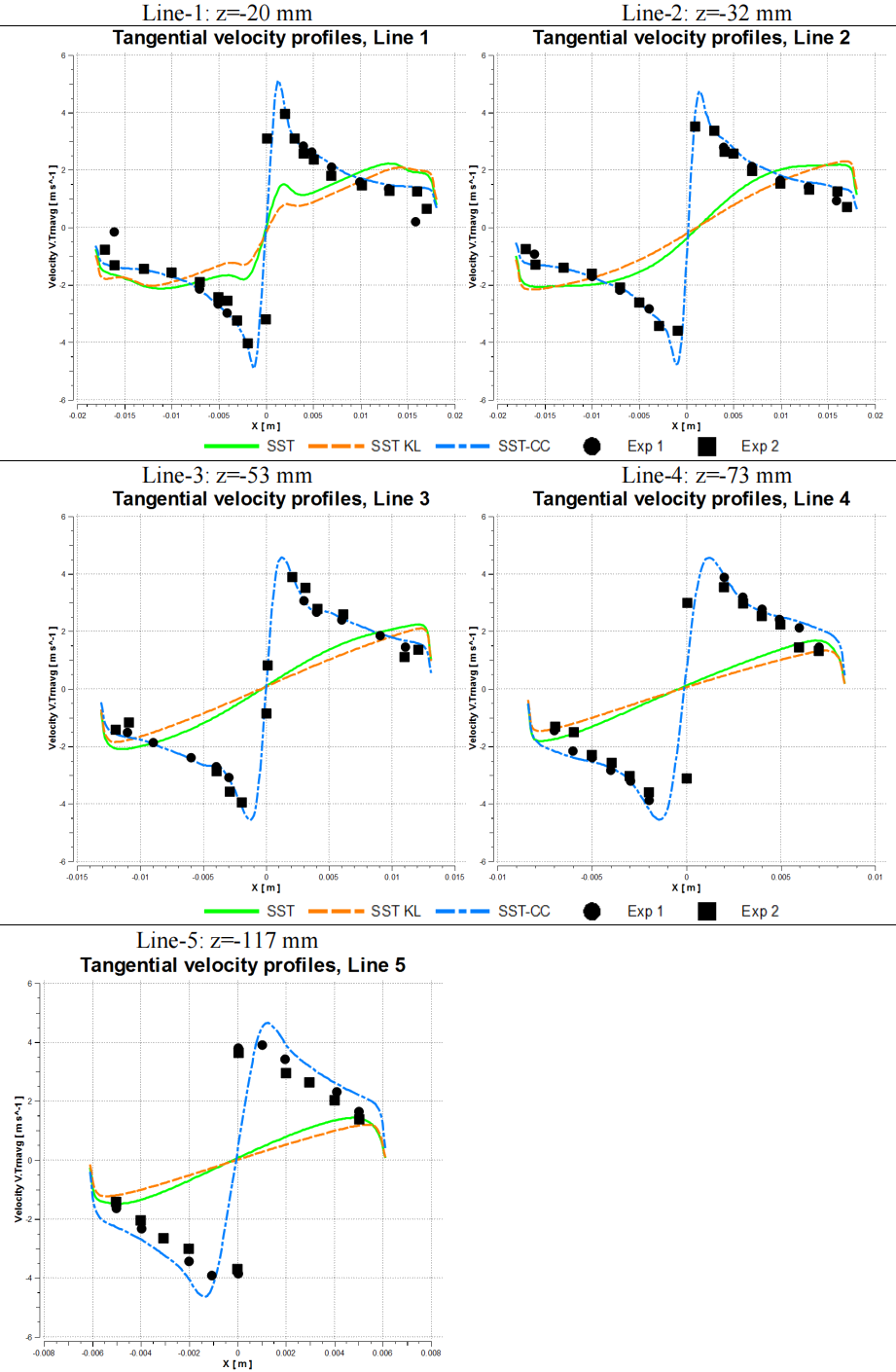
图 57 显示了计算得到的图 56 所示水力旋流器中不同 z 位置的切向速度对湍流模型选择的敏感性。其中z = -20 毫米的位置正好位于涡探测仪的下方。从实验数据中可以看到典型的兰金涡，在外侧半径处显示出无粘涡，在靠近轴线处显示出实体旋转。原始 SST 模型无法预测大半径处的无漩涡，而是倾向于在任何地方都出现实体旋转。通过对 SST 模型应用曲率校正方法，可以显著改善这种情况。曲率校正的主要机制在于捕捉轴线附近固态旋转 的稳定效应，这导致该区域湍流（以及涡粘度）的大幅减弱。在比较中还包括 SST 模型与Kato-Launder Production限制器（见 9.2.3）的组合，这种修改确实会影响涡流，因为涡度和应变率不再相等。不过与曲率修正相比，其影响很小。

测量位置如图所示。

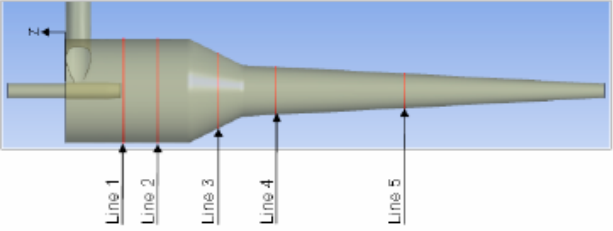
计算结果比较如图57所示。

注：系列翻译自《Best Practice: RANS Turbulence Modelingin Ansys CFD》，作者F.R. Mentor，2022

”

（待续）