利用Fluent模拟浸没在流体中的球体的尾流和流动分离的流动状态，并将计算结果与文献资料中的数据进行比较。

文献：Tabata, M. & Itakura, K. (1998). A precise computation of drag coefficients of a sphere. International Journal of Computational Fluid Dynamics, 9(3-4).

”

1 问题描述

计算网格如图所示。

几何模型：利用轴对称对球的几何截面进行二维建模，球体直径为1 m，球体周围的圆形流体域半径为50 D。

流动条件：入口速度1 m/s。

介质属性：密度1 kg/m3，粘度0.02 kg/(m-s)。

流动雷诺数：

采用层流计算。

文献中得到的球体阻力系数与雷诺数关系如下表所示。

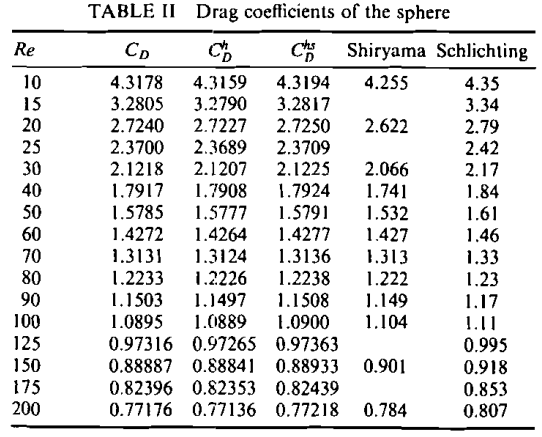
雷诺数50所对应的阻力系数为1.5785。

2 几何与网格

在SpaceClaim中根据几何尺寸创建几何模型。

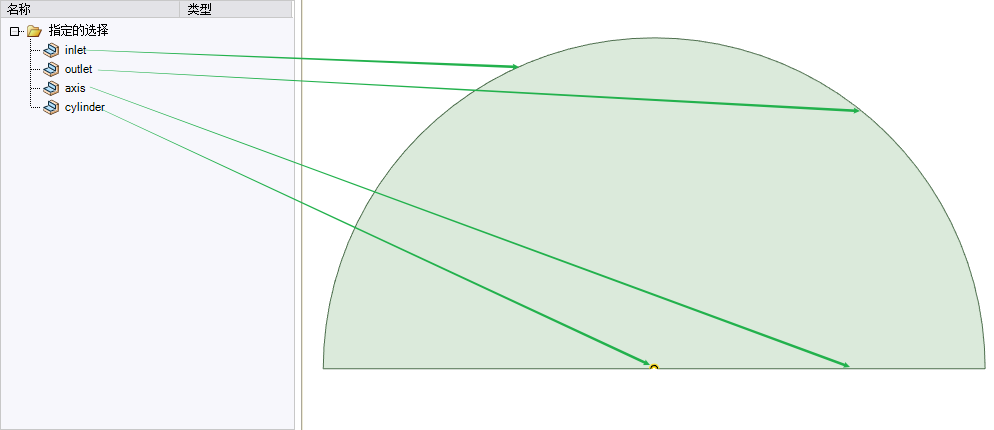
创建边界命名。

在SpaceClaim中生成网格。

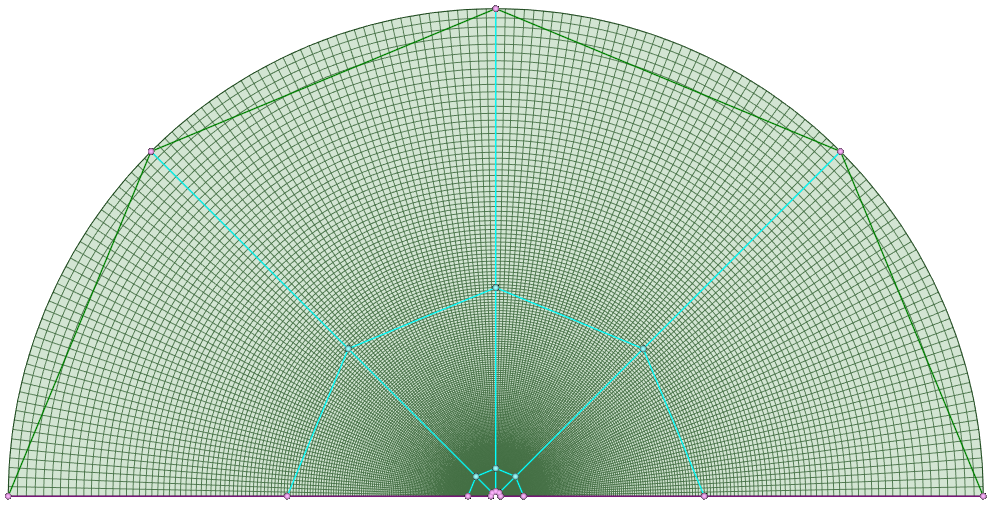
3 Fluent设置

3.1 General 设置

• 选择Axisymmetric使用轴对称模型

3.2 Models设置

• 层流计算采用Laminar模型

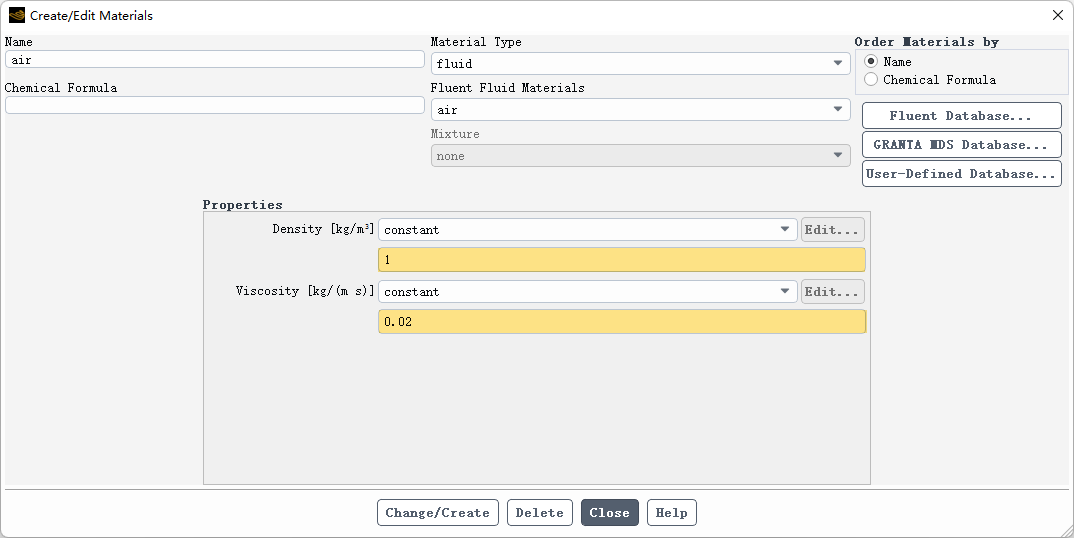
3.3 Materials设置

• 指定流体密度为1 kg/m3，粘度为0.02 kg/(m-s)

3.4 边界条件设置

1、inlet设置

• 指定入口速度为X方向1 m/s

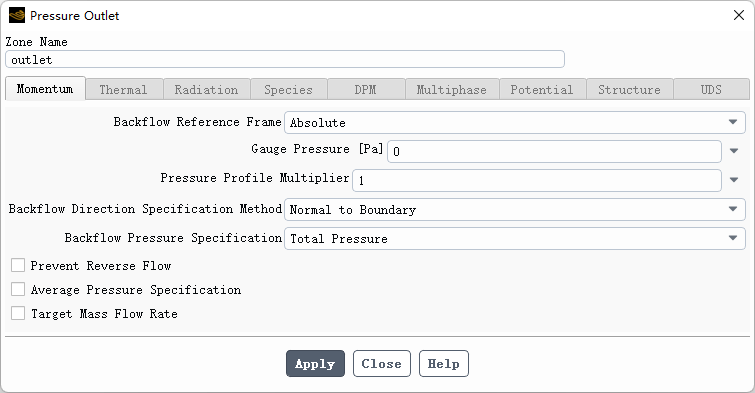
2、outlet设置

• 出口边界采用默认设置

3.5 参考值设置

• 如下图所示指定参考值

参考值用于计算阻力系数：

其中为空气阻力，为空气密度，为是物体相对于空气的速度， 为阻力系数，为物体的迎风面积。这里球体的迎风面积：

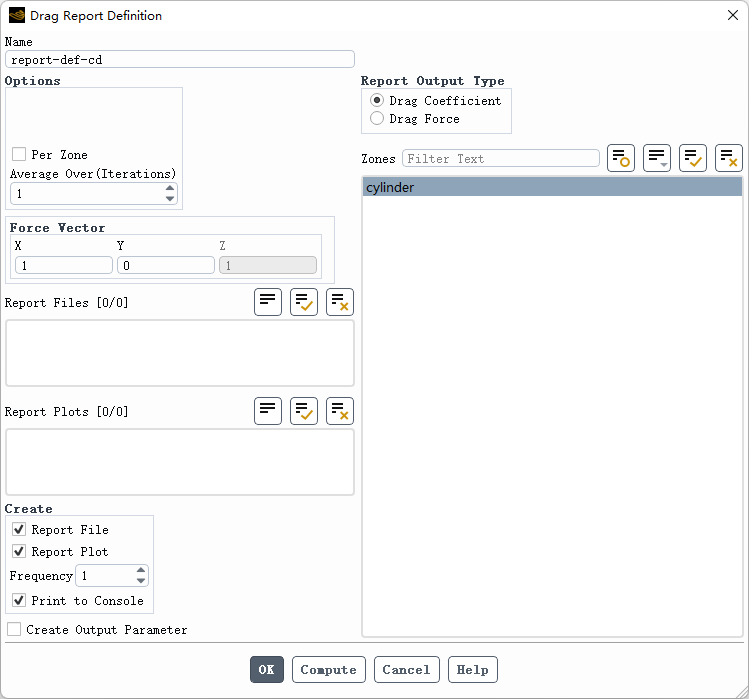
3.6 物理量监测

• 监测球体表面的阻力系数

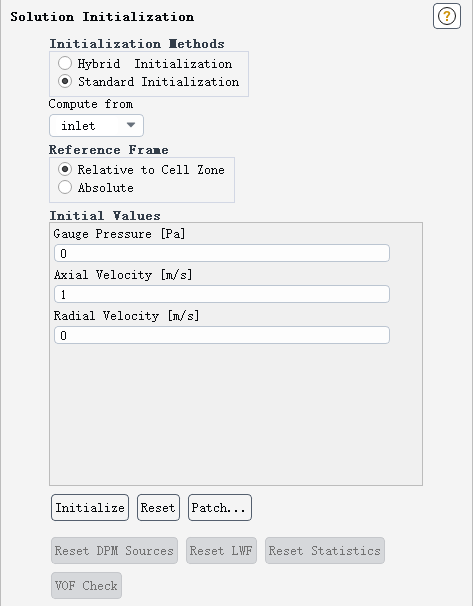
3.7 初始化计算

• 利用入口进行初始化

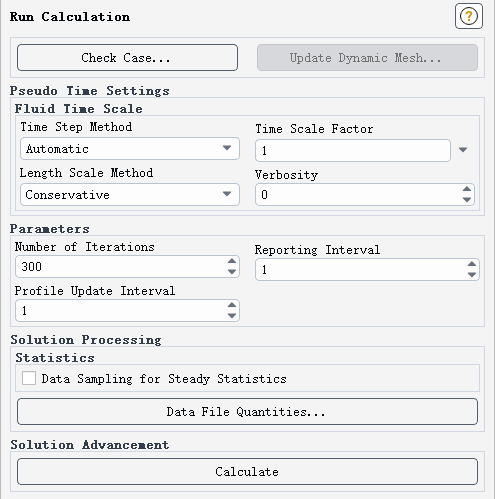
3.8 迭代计算

• 迭代计算300步

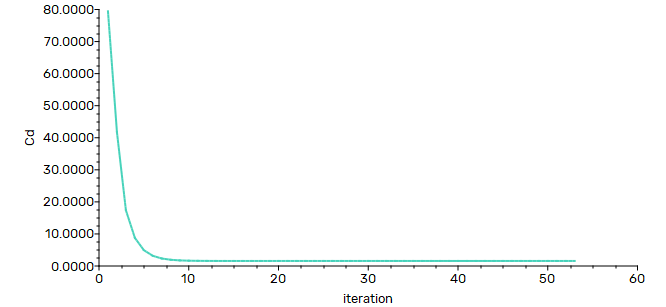
• 阻力系数监测曲线

4 计算结果

• 球体周围压力系数分布

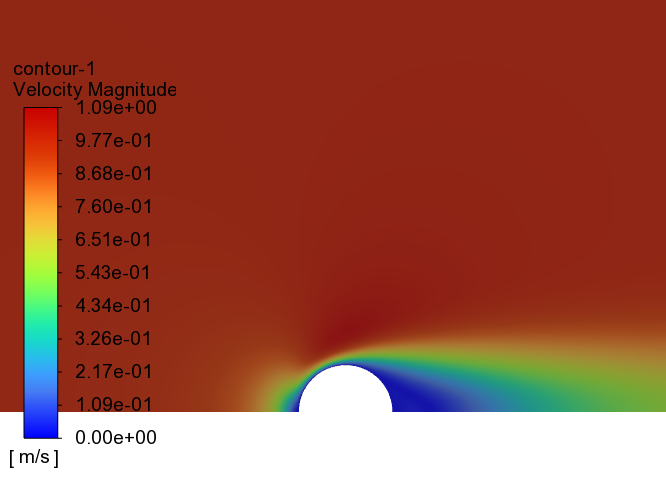
• 球体周围速度分布

• 得到阻力系数值

如下图所示，输出的阻力系数值为1.5743207。

与文献2中的数据对比：

误差还是比较小的。

（完）