当我们打开一瓶有年份的纯正葡萄酒,倒出部分酒液在酒杯中,然后轻轻地摇晃酒杯,让酒液在杯壁上均匀地旋转,当停止摇杯后,酒液便会形成一条条液柱沿着杯壁缓缓地向下流动,并在杯壁上留下一道道酒痕,人们为它起了一个动听的名字“葡萄酒的眼泪”。
葡萄酒真的会流泪吗?为什么会形成酒泪呢?其实这些酒泪是由马兰戈尼效应造成,它是一种由两种流体的接触面间的表面张力梯度造成的传质现象。
酒泪
1865年,开尔文勋爵的弟弟,物理学家 James Thomson 最早提出了酒泪一词。意大利物理学家 Carlo Marangoni 在他的博士课题中继续研究了这一现象,并在 1865 年发表了他的研究成果。马兰戈尼效应以 Marangoni 先生和他的研究工作命名,是酒泪和其他一些表面化学和流体流动现象背后的成因。

酒泪沿玻璃杯内壁滑落
马兰戈尼效应
研究一下您的玻璃杯,看到酒泪了吗?没有的话,可能是因为您选择的葡萄酒酒精含量较低。如果希望看到酒泪,建议您选择酒精含量较高的葡萄酒,它更可能出现酒泪。在酒精含量较低的葡萄酒中,葡萄酒与空气界面上酒精浓度与表面张力的差异较小,因此很少会出现酒泪。上图中所用葡萄酒的酒精含量为 13.5%,虽然相对较低,已经能够产生酒泪。
表面张力是两相接触面的一个属性,它描述了将该界面的表面积增大一个单位所需的能量。您还可以将表面张力看作创建每单位长度的新表面积所需的能量。下图显示了液相中与其蒸汽接触的分子状态。表面分子(红色)与蒸汽分子(橙色)在向上方向的相互作用极少,因此它们将经历不对称的力,这种力将液体表面拉紧在一起。液体主体中的分子(蓝色)会在所有方向发生相互作用。为了拓展液体的表面积,主体分子需要向表面移动,打破向上的相互作用,这就需要能量。这就需要能量。
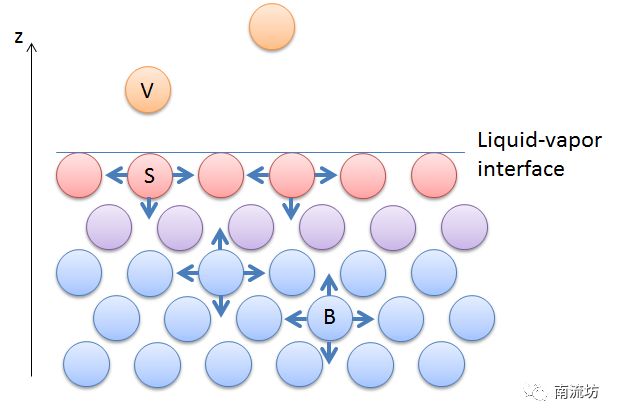
正与其蒸汽发生相互作用的液体中的表面张力。表面分子(红色)经历了不对称的相互作用。下方紧挨着它们的分子(紫色)所经历相互作用的对称性略高,主体分子(蓝色)则将经历着更加对称的相互作用
由于氢键的关系,液体水之间的相互作用非常强,由于需要打破较强的相互作用,因此它拥有相对较高的表面张力。液体-蒸汽接触面的表面张力依赖于液体主体内分子间相互作用的强度。上图中,马兰戈尼效应是指由表面张力梯度沿液体-蒸气接触面造成的流动。这类梯度可能由沿此表面的溶液成分或温度差异造成。
我们可以向盘中倒入薄薄的一层水来观察它是如何实现的,向盘中加入发光物或其他较轻的材料,以便更好地演示这种效应。发光物分子具有亲水性,或者说它很爱水,这使它能与水发生相互作用。表面中部滴入一滴皂液、酒精、机油或其他任何拥有收缩性表面张力的液体,此时所有发光物都将立即离开中央流到表面边缘处。
倒入皂液后,皂液分子会在水表面形成一层薄膜,这层膜仅有单层或几层分子厚。皂液覆盖的表面和水面之间会产生表面张力差,使得皂液膜开始扩张,发光粒子流向侧边,这就是马兰戈尼效应。最终,肥皂分子覆盖整个表面,表面能降低,因为表面的水分子也能与皂液分子的亲水端发生相互作用。
下一张图在分子层面演示了这个实验。发光粒子拥有亲水表面,所以它们更易与水而非皂液发生相互作用。随着皂液覆盖表面,它们被挤到盘边,因为它们更“希望” 继续与水分子发生相互作用。
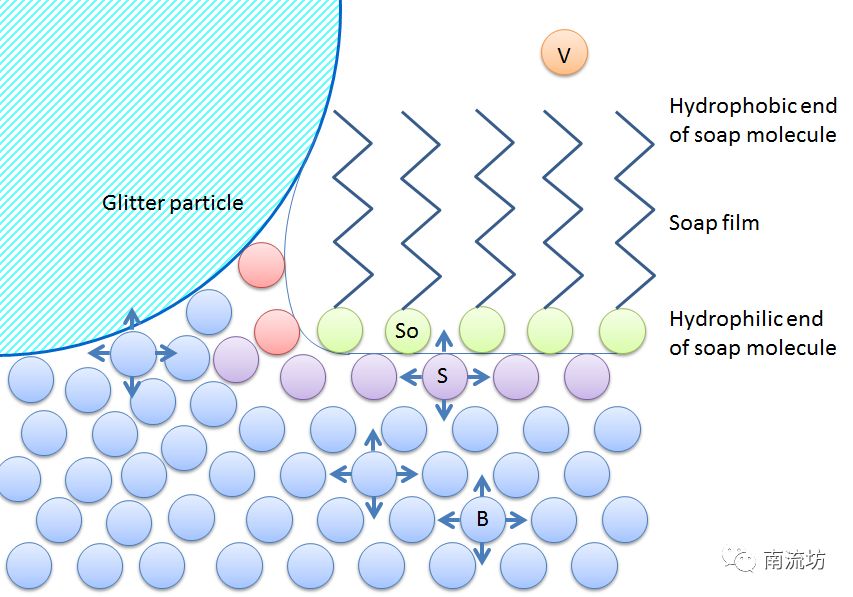
向水中滴入皂液后,表面张力改变。皂液为绿色,是一个带有碳氢化合物“尾巴”的离子。水的主体部分为蓝色,红色为自由水面,紫色为被皂液覆盖的表面或紧挨着其他表面水分子的分子
向盘中倒入水和发光物,然后在中间滴入皂液,发光物冲到盘边。为什么? 因为水的表面张力高于洗洁精。

酒泪是在玻璃杯壁、葡萄酒和空气的三相结点处形成的一个弯月面。在此位置,流体会松松地挂在玻璃杯的表面。弯月面的形成原因是,玻璃杯壁的表面与发光粒子一样均为亲水性质。由于乙醇的平衡蒸汽压高于水,葡萄酒中的酒精会持续从表面蒸发,而且蒸发速率快于水的蒸发,弯月面中的情况也是如此。弯月面中酒精浓度的下降更快,因为体积较小,所以表面积相对更大。因此,这会在弯月面和葡萄酒与空气间的平坦接触表面之间形成浓度差,随后将造成表面张力梯度,使弯月面沿着玻璃杯壁向上移动。
随着弯月面开始在玻璃杯的壁面形成一层膜,其中的酒精进一步挥发,造成了更大的表面张力梯度。更多的葡萄酒被拉到玻璃杯壁上,直到形成液滴。此时重力将起作用,酒泪沿玻璃杯壁流回葡萄酒的主体内。
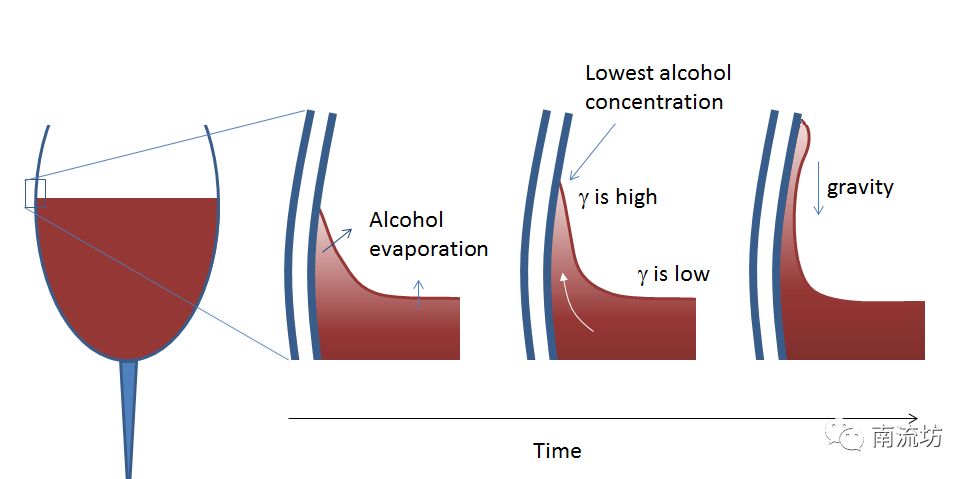
弯月面和葡萄酒平面之间的表面张力 (γ) 梯度形成了酒泪
借助射流非稳定模型模拟马兰戈尼效应
我们可以用 COMSOL Multiphysics 和微流体模块来模拟马兰戈尼效应。我们将利用射流非稳定性教学模型来演示这一概念。模型模拟了一台喷墨打印机中一个无限长的射流因为表面张力系数随空间的变化而被破坏。
此模型有三种求解方法:移动网格、水平集或相场方法。您还可以在案例集锦中看到有关移动网格和水平集建模方法指导的 PDF 文件。与水平集方法相比,移动网格方法更快,更易使用,正如 Fabrice Schlegel 的博客“我应该选择哪个多相流接口?”中所介绍的那样。但如果玻璃杯侧壁上葡萄酒层的厚度有限,我们将只能使用移动网格方法来模拟马兰戈尼效应。在酒泪和剩余葡萄酒之间可能不存在干燥区域。那样的话,我们将必须使用水平集或相场方法。
射流非稳定性模型包括一个圆柱形的流体域,半径 20 微米,高度 60 微米。域中包含一个半径为 5 微米的水柱。我们需要定义墨水的属性,比如密度、动力粘度以及表面张力系数。
我们使用层流两相流,移动网格接口来求解该模型,并在移动网格几何上绘制出几何结构。本仿真中,接触面没有厚度,通过边界进行表征。这更适合实际的网格密度。接口计算了 Navier-Stokes 方程和边界条件,然后将其转换为固定网格。
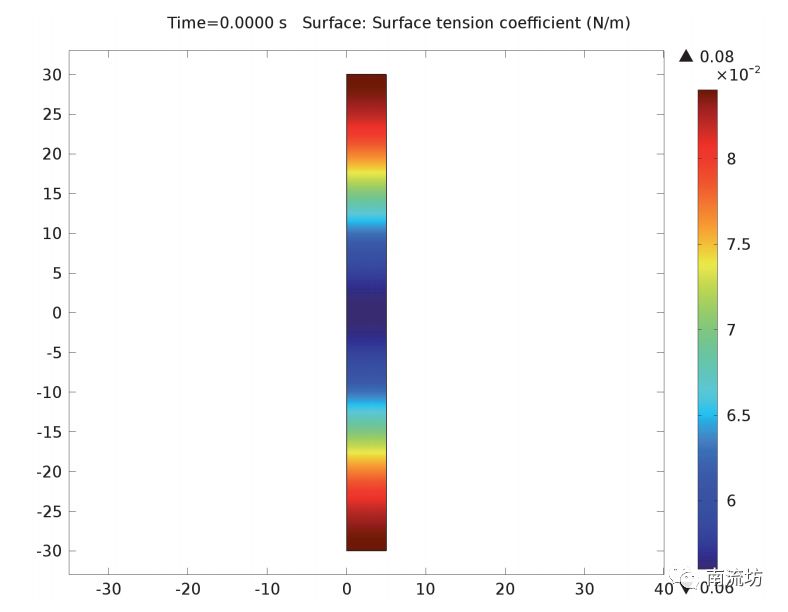
射流非稳定模型中喷墨打印机模型中的柱体
可以轻松地在层流两相流,移动网格接口中耦合其他物理场,它要比水平集和相场方法更快、更精确。但移动网格方法无法处理拓扑变化,因此只能用于计算液滴被打破之前的情况。层流两相流,水平集方法接口计算了由 Navier-Stokes 方程、周期性边界条件以及点设定描述的速度场与压力。
下方的结果显示了利用水平集方法进行的模拟,显示出射流在 6 个时间周期后被破坏为液滴。首先,液体形成了一个完美的圆柱,但表面张力的变化会扰动射流,并产生一个力,这个力最终会因表面曲率的关系将射流破坏为液滴。
模型的液体区域为射流,由于表面张力随时间变化的关系被破坏
以下是一个关于的科学小实验的视频
来源:公众号“COMSOL”
本篇文章来源于微信公众号: 南流坊








评论前必须登录!
注册