荡漾的小船产生水波,高速飞行的喷气机产生湍流。数学家和物理学家相信,对纳维-斯托克斯方程的理解,可以找到对风和湍流的解释和预测。虽然这些方程在19世纪就被提出,但我们对它们仍知之甚少。我们面临的挑战是在数学理论做出实质性的进步,从而揭开隐藏在纳维叶-斯托克斯方程背后中的秘密。
——克雷数学研究所
物理学中包含许多不同的方程式,这些方程描述了从微观世界的粒子行为到宏观宇宙的演化。在所有的物理方程中,用来描述流体如何流动的纳维-斯托克斯方程(简称NS方程)被认为极具挑战性的,因此被克雷数学研究所列为七个“千禧年大奖问题”之一(无论是谁解决了其中一个难题,都将获得100万美元的奖励)。
NS方程可以看作是牛顿第二定律的流体版本。牛顿第二运动定律告诉我们:
质量 × 加速度 = 力
它描述了一个物体的速度在外力作用下会如何改变。
在NS方程中,等式左边包含的是密度和加速度,右边包含了压强的变化、内力的变化,还有作用在流体上的外力的变化。
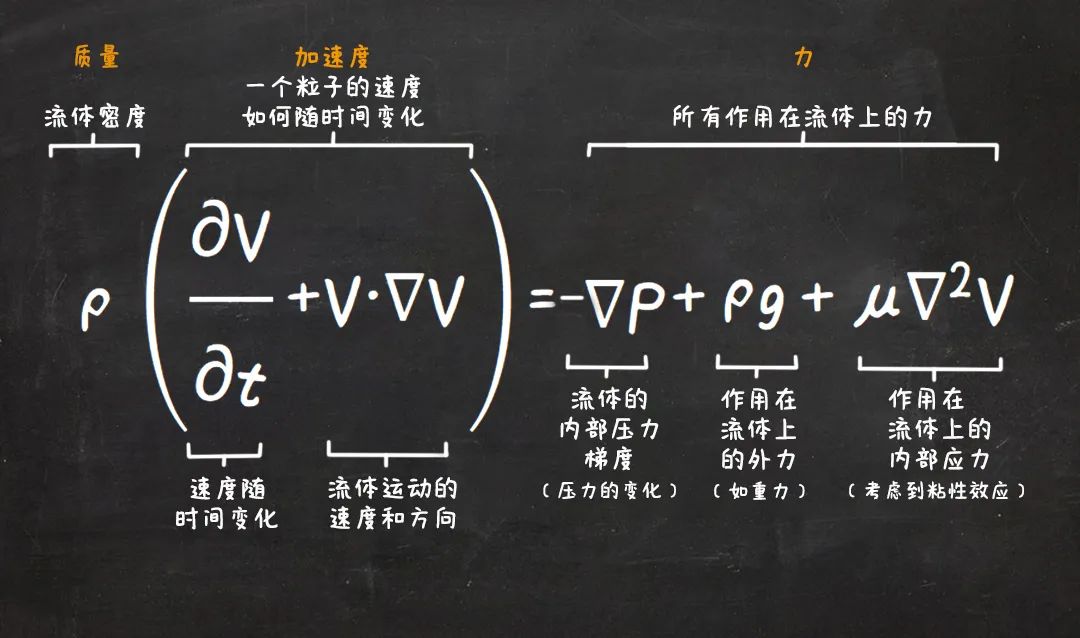
NS方程的历史可追溯到19世纪20年代,现已被广泛用来模拟各种物理系统,例如流出水龙头的水,或流过飞机机翼的气流。从物理学的角度来看,NS方程运作良好,似乎有着非常可靠的预测能力;但在数学家心中,它们的数学合理性却一直存疑,数学家想要证明无论对于什么样的流体,也无论对其流动的预测发生在多远的未来,这些方程在数学性上都是正确的。他们想要知道的是有没有可能在某些情况下,这些方程会出现故障,产生不正确的答案,或者根本无法给出任何答案。
证明NS方程的解永远存在是这个千禧年大奖问题的核心所在。那么,为什么这在数学上会是如此困难的问题?
湍流便是这其中的原因。湍流是有序流动的流体变化成的看似不可预知的漩涡,例如一缕青烟在空气中扩散,牛奶和咖啡的混合,生活中的现象都与湍流有关。然而,熟悉并没能孕育出理解,毫不夸张的说:湍流是物理世界中最难以理解的部分之一。
据说,对量子力学做出巨大贡献的物理学家维尔纳·海森堡(Werner Heisenberg)曾经说:“当我见到上帝时,我想问他两个问题:为什么会有相对论?为什么会有湍流?我相信他一定会有第一个问题的答案。”这个说法的真实性虽无从考证,却道出了许多科学家对湍流的感觉。
在探讨湍流之前,我们可以先来说说什么是非湍流。一个简单的非湍流例子就是一条平稳流动的河,河流中的每个部分都以相同的速率向相同的方向运动。而湍流就是阻挠了这条河平稳流动的存在,它让不同部分的河流以不同的速度向不同方向运动。物理学家首先将湍流的形成描述为是平稳流动的涡流,然后在这个涡流中形成了更小的涡流,更小的涡流中又进一步形成更加细小的涡流……这个过程循环往复,使得流体分裂成许多离散的部分,它们各自运动,又相互作用。

对科学家来说,他们想要了解的是平稳的流动会如何分解成湍流,以及如何模拟已产生湍流的流体的形状变化。而数学家想要解决的问题则更为基础的问题:证明方程的解永远存在,即探寻方程是否能从任何起始条件开始,对任意流体进行无限的描述。
因此,总结说来,NS方程难题可以被分为两个部分:
第一个是关于方程解的存在性;
第二个是关于这些解是否有边界(是有限的值)。
第一个部分说的是,对于一个数学模型来说,无论它多么复杂,若要想代表这个物理世界,那么它首先必须有解。目前在实践中,虽然NS方程为流体的运动提供了许多很好的预测,但是这些都是NS方程的完整解的近似。而之所以会产生近似值,是因为我们通常没有简单的数学公式可用,只能用计算机进行近似的数值计算以求解这些方程。虽然科学家相信这些近似解就是正确的,但在数学上仍缺乏一个能正式表明这些解确实存在的证明。
第二部分则需要探讨这些方程的解是否会出现奇点,或者说无穷大。这个问题之所以重要,是因为如果在NS方程中存在这样一个无法计算的无穷大值,那么NS方程就会失效,解也不复存在,这直接表明了我们可能漏掉了某些重要的、尚未可知的物理学。流体力学的历史充满了简化版的NS方程的解,这些方程产生奇异解。在这种情况下,奇异的解往往暗示着一些以前在简化模型中没有考虑过的物理现象。识别出这种新的物理现象促使着研究人员进一步地完善他们的数学模型,从而提高模型与现实之间的一致性。
所以,对存在性和光滑性问题的追问是为了让我们彻底地明白在物理世界里真正发生了什么。许多数学家都尝试过寻找这个问题的答案,但都以失败告终。一些物理学家认为,对强耦合的理解的新进展,或许会有助于破解NS方程。
每当我们从数学角度谈论物理方程时,很自然的就会想要知道:这些会改变我们对物理世界的看法吗?经过近200年的实验,我们可以清楚地看出这些方程是有效的:由NS方程预测的流动与实验中观察到的流动总是相符的。如果你是一个实验物理学家,或许这样的一致性就已经足够了。但是,数学家对存在性和光滑性问题的追问,才能让我们彻底地明白在物理世界里真正发生了什么,这有助于我们准确地看到对有着任意初始配置的流体是如何发生瞬时变化的,甚至能精确定位湍流的开始。
来源:公众号“原理”
本篇文章来源于微信公众号: 南流坊








评论前必须登录!
注册