数数有几个零，就知道对不对

1 数据越密集，结论越混乱

 

先问个问题：桌面是平的吗?

以一米的长度看，桌面很平

以一毫米的长度看，桌面起伏不平

以一微米的长度看，桌面崎岖不平

不是说测量越细致越准确吗？为什么越细致越不知道桌面的特性。

观察的尺度要与你的问题匹配，过度密集的数据，只会将你的眼光缩小到很小的细节而失去了全局。当然过度稀疏的数据也会遗漏你要观察的现象。 

我们做仿真，往往需要沿着一条曲线求出斜率。有人为了求得“准确”的斜率，将计算的X间隔缩得很小，认为间隔越小，数据的精度越高。岂不知短距离取值，变化量与偏差在一个量级，当地的变化量已经被当地的偏差淹没，得到的当地斜率反而失真。不如长距离取值，好像数据间隔大品质不好了，数据反而更能够反映真实。

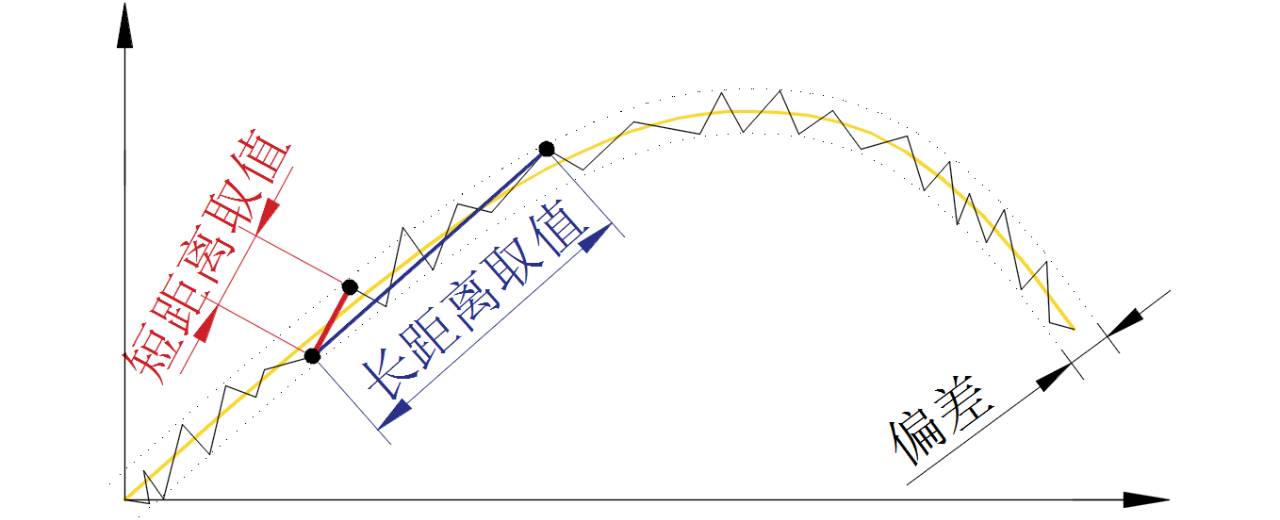
假设计算偏差是10%，短距离取值的物理变化是5%，用这个数据求斜率，就是一个被偏差污染的值。长距离取值的物理变化是50%，偏差是相对小量，求得的斜率更可靠。 

如果你的计算偏差是10%，你又何苦分析5%变化的现象。

只有你将计算偏差降低到5%以下，你才有资格谈论5%的变化。

 

  

2 湍流与股票可以预测吗？

你会说湍流不可预测，股票也不可预测，如果可以预测其中任何一个，你都能名利双收。 

多么混乱的现象背后都有规律，但是这个规律只是能告诉你大方向，不能预报细节。 

只要你站在更高的尺度上观察，湍流是否发生完全可以用雷诺数判断，湍流的基本构成也有数学描述，从宏观角度，湍流可以准确预测。 

雷诺数大到某个值后，会发生湍流，只是你无法指出在哪个时刻、哪个位置出现湍流。好比北京道路上的车多到一定程度必然会发生大堵车，但是谁也无法告诉在哪个路口、什么时刻会发生。 

股票上升后必然会跌落，经济形势好坏会影响股票。以几年的时间长度看股票波动，曲线可以清楚地告诉你现在的价值是否是低点。看当天每分钟跳动的曲线，这是无数随机因素的瞬时影响效果，谁也无法判断下一时刻的走向。

伟大的认知，不代表知道细节。

你可以看出海上波浪翻滚的方向，但是无法预告每一个小水滴的运动。

 

 

3 数数有几个零，就知道对不对 

有一次同事找我，说是昨晚熬了一夜，用两种算法算出来的数不一样，分别是0.15和0.1。他很苦闷不知道哪个算法准确，或者都不对，请我帮助再算一遍。我想了想说，这两种算法我都不懂，但是等我一分钟，也许可以解决。我立即找到使用这个数的人，问他这个数是0.1还是0.2对设计有多大影响，他轻松地说，不到1.0影响都不大。我马上回去告诉那个倒霉的同事，0.15还是0.1都行，随便给一个数，这两个算法都可以用。

整个过程我没有学习算法也没有深究这个数，我只是先确定了量级的影响。 （有人指导我，应当取中间值1.25，我说我不在乎。）

量级分析可以让你第一时间确定因素的重要性，如果发现这个因素不重要，请放过去，留出时间去解决影响量级大的重要因素。这个故事你可以认为是偷懒的借口，也可以认为是研究的方法。 

很多人都希望准确了更准确，每一个数准确到小数点后面很多位。其实每个数据都精细不一定代表做事情精细，反而透露出做事人的心虚，好像在说“我都这么精细了，结果必须准确”。

100个因素中，即使99个因素都准确到1%，只要有一个因素误差100%，所有的工作都白费。

真正的精细是识别出误差最大的因素，全力去解决掉，暂时将误差小的因素视而不见。 

对小误差视而不见，这个观点已经被无数人斥责。他们很正义地指责这么做态度不端正。他们怀揣端正的态度，遇到第一个数据就要做到精确无比。像个鸵鸟似的紧紧抱着自己的头，忘记一个硕大的身体暴露给敌人。最后错到姥姥家了，还委屈的想，为什么小数点后面第十位都做对了，最终却有100%的误差？ 

还有人想用他表现的端正态度来“证明”，他的人品是可信的，所以他的结果也是可信的。鸵鸟把脑袋抱得越紧，屁股翘得越高。局部的过度精细，会使人更加安心地忽略最大误差。 

量级分析永远是所有分析的第一步。

先确定有几个零，再确定前面是1还是2。

千万不要让别人看到，他们会嘲笑你三观不正。

本篇文章来源于微信公众号: 陆姐说