本文描述在Fluent中进行浮力驱动流及自然对流模拟的基本方法。

封闭区域内的自然对流模拟结果取决于区域内的流体质量。除非密度已知，否则无法得到质量。因此对于封闭区域自然对流模拟须采用以下方式之一进行模拟：

• 采用瞬态计算。在这种方法中，初始密度根据初始压力和温度计算，因此计算区域内的初始质量是已知的。计算区域内的质量在所有的时间点都必须保持守恒。如果计算区域内的温差很大，则必须采用此方法进行计算。
• 使用Boussinesq模型进行稳态计算。在此方法中，将指定一个恒定密度，以便正确地指定区域内的质量。这种方法只有在区域内的温差很小时才有效。如果温差很大，则需要使用瞬态计算方法。

注：对于封闭的计算区域，只能在fixed operating pressure下使用incompressible ideal gas，其不能与floating operating pressure一起使用。不过可以在固定或浮点的工作压力下使用ideal gas。

”

1 Boussinesq模型

对于许多自然对流流动，使用Boussinesq模型的收敛速度要比使用流体密度作为温度函数时更快。除动量方程中的浮力项外，该模型将密度视为常数：

式中，为流体密度，其为常数；为操作温度；为热膨胀系数。式(1)是通过通过使用Boussinesq近似来从浮力项消除而获得。只要计算区域内的密度变化量很小，这个近似就是准确的。具体来说，Boussinesq近似在时有效。

注意：如果区域内的温差较大，则不能使用Boussinesq模型。此外，该模型还不能用于组分输运、燃烧或反应流。

”

2 求解浮力驱动流问题

可以采用以下步骤模拟浮力驱动流问题：

1. 激活能量方程。通过右键选择模型树节点Energy，弹出的对话框中激活选项On开启能量方程。
2. 定义操作条件。打开Operating Conditions对话框，如下所示。

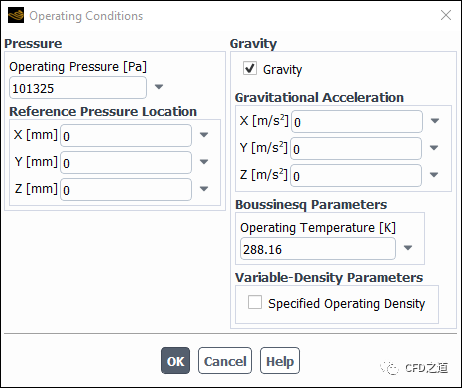
进行以下设置：

• 激活选项Gravity，并指定重力加速度分量。
• 如果材料密度使用了incompressible ideal gas，则需要正确地设置Operating Pressure，该参数一般为非零值。
• 根据是否使用Boussinesq近似，需要指定以下的适当参数：
• 当使用Boussinesq模型时，设置参数Operating Parameters，并在材料参数设置面板中指定介质的Desity为boussinesq，并指定一个常数密度；在材料参数面板中设置材料介质参数Thermal Expansion。
• 当不使用Boussinesq模型时，对于单相流动，激活选项Specified Operating Density并设置参数Operating Density；对于多相流动，Fluent默认设置操作密度为minimum-phase-averaged，用户也可以自己输入参数。需要注意的是，如果使用的是可压缩气体模型（理想气体或真实气体），则应当将Operating Density设置为0。除此以外，用户还需要在材料介质对话框中将介质密度设置为温度的函数。

3. 定义边界条件。在压力入口和出口边界指定的边界压力是重新定义的压力。通常，如果没有外部施加的压力梯度，则应在Fluent模型的入口和出口边界输入等效的压力。
4. 设置Methods。若使用压力基求解器，建议在Methods面板中设置Pressure的离散格式为PRESTO!。

3 操作密度

当不使用Boussinesq模型时，动量方程的体力源项中将会出现操作密度。这种形式的体力项源自Fluent中对压力的重新定义，如下所示：

其他区域的静水压力为：

默认情况下，Fluent通过对所有网格进行平均来计算操作密度。在某些情况下，如果明确地指定操作密度而不是让求解器计算，可能会获得更好的结果。例如，如果要求解具有压力边界的自然对流问题，重要的是要了解在公式7-67中指定的压力。虽然知道实际压力，但仍需要知道操作密度才能通过确定，此时应该明确指定操作密度，而不是使用计算得到的平均值。

在一些问题中，指定操作密度可以善收敛行为，而对计算结果没有影响。在这种情况下，可以使用近似的体积密度值作为操作密度，并确保选择的值适合该区域的特征温度。

需要注意的是，如果所有流体材料都使用Boussinesq模型，则操作密度不会出现在动量方程的体力项中，此时无需指定操作密度。

4 高瑞利数流动模拟

在求解高瑞利数流动()时，应遵循下面概述的步骤之一以获得最佳结果：

第一个过程使用稳态方法：

1. 使用较低的Rayleigh数值(例如)开始求解，并使用first order格式得到收敛结果
2. 若要更改有效瑞利数，可以更改重力加速度的值(例如，从9.8更改为0.098，以将瑞利数减少两个数量级)
3. 使用生成的结果作为较高Rayleigh数的初始值，并使用first order格式进行较高Rayleigh数计算
4. 在获得一阶格式的收敛解之后，继续使用高阶格式进行计算

第二个过程使用与时间相关的方法来获得稳态解：

1. 从瑞利数相同或更低时获得的稳态解开始求解
2. 估计时间常数：

式中及分别为长度尺度与速度尺度。

使用的时间步长为：

使用较大的时间步长可能会导致发散。

3. 在经过=0.05~0.09的振荡衰减后，计算可达到稳定。请注意，是公式(4)中估计的时间常数，是以Hz为单位的振荡频率。通常该求解过程可能需要多达5000个时间步长才能达到稳定状态。

（本文译自Fluent UserGuide 7.3.1）