CFD仿真的误差有下面几大来源：

• 模型误差。简单来说，模型误差就是计算模型与真实物理世界之间的差异。这部分误差占整个仿真误差的大头。
• 数值误差。指的是利用数值方法对计算模型进行求解的过程中产生的误差。

1 模型误差

模型误差是主要的误差来源。

产生模型误差的原因非常多，下面是一些常见的模型误差：

• 不合理的模型简化。在产生计算模型的过程中，忽略了不应该忽略的物理现象或物理条件。例如将散热壁面简化成绝热壁面，将对流边界简化成常温边界等。
• 不精确的边界数据。计算模型的求解依赖于边界条件，然而计算模型的边界条件往往难以精确获取，甚至于边界位置都是人为确定的，现实中并不存在。
• 不明确的初始条件。对于一些探索演化过程的模拟来说，准确的初始状态非常重要。然而现实中难以准确描述。

模型误差依赖于建模者的理论背景及试验数据。现实中的工程问题异常复杂，如何从复杂的问题中简化出既能够计算，又保留原始问题特征的计算模型，是仿真者技术水平的体现。

模型简化得怎样，需要通过试验来验证。比如说在简化过程中忽略了一些影响因素，那么这个忽略对计算结果的影响到底有多大，是否确实可以忽略，都有必要通过试验进行验证。

如下图所示的简单问题。

比较常见的工程描述（反正我碰到很多次）：桌面上放置有一个温度比较高的发热物体，想知道10 s后物体表面及周围空间的温度分布。

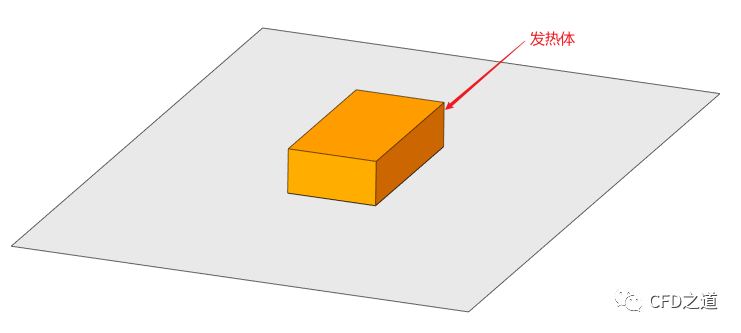
这个问题描述并不明确。首先，“温度较高”对于计算来说毫无意义，应当明确。其次想要知道10 s后的温度分布，必须明确发热物体与外界环境之间的散热关系。

要想计算10 s后物体的温度分布，需要明确物体发热的原因，这对于后续的温度计算非常重要。这可能有多种原因：

• 物体温度已知，但外部空间温度位置。
• 物体发热功率已知，但物体温度及外部空间温度均未知。

两种原因会导致计算模型存在差异。对于第一种，建模的时候可以将固体区域去掉，而第二种则需要保留固体区域。但到底是哪一种情况，则依赖于试验测量。当然工程中大多数情况倾向于第二种，毕竟维持一个物体温度为恒温是个技术活儿。

那就说第二种情况，已知发热体的热功率，那这个热功率是测量得到的还是理论值？如何保证这个数据是可靠且有效？

还有个问题，要计算外部空间温度分布，需要建立计算区域。如下图所示建立一个外部散热空间。

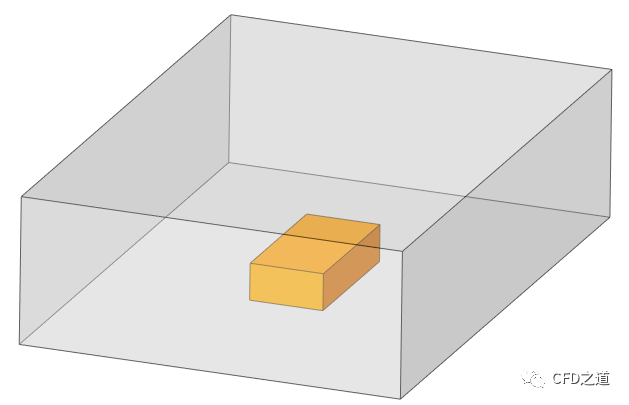
这里同样有很多的麻烦事儿要确定。

1. 计算区域建多大？这个区域的大小似乎很随意，找不到一个明确的约束。比如这是个露天的桌子，那外部空间可就是无穷大了。计算的时候当然不能取一个无穷大的计算区域。那搞了个有限的区域，你确定计算区域大小对计算结果没有影响？
2. 区域的边界条件怎么定？人工创建了一个外部计算区域的同时，也增加了额外的边界输入。比如上图中外部空间的6个面，怎么给边界？这个边界本来是不存在的，是人工虚构出来的。
3. 发热体与桌子之间的接触。接触不良会产生极大的接触热阻，其对热传导会产生很大的影响，这个怎么确定？
4. 需要考虑哪些传热方式？对流？传导？热辐射？
5. 物体和介质的物性参数和热参数会不会随温度变化？

上面的这些问题，都需要试验数据做标定。这里举的是个很简单的例子，实际的工程问题要比这个复杂得多。需要注意的是，模型误差是最主要的误差来源，处理不好的话，产生的就不是误差，而是错误。

然而现实中情况是：甲方扔给你一个问题描述，让你去做仿真计算，最后还要将你做的仿真结果与他们的试验测量数据进行比较，以此来验证你的水平。同时还有个让人无法反驳的理由：做仿真不就是为了不做或少做试验么？

就问尴尬不尴尬？

2 数值误差

数值误差是在计算模型确定之后，在对计算模型进行数值求解的过程中，数值算法造成的误差。

数值误差的来源也非常多，最常见的无异于以下几种：

• 网格。网格数量不足或低质量的网格都会造成数值计算误差。
• 离散方法。将偏微分方程转换为代数方程过程中，为了数学处理方便舍弃一些项造成的截断误差。
• 迭代误差。求解代数方程组的过程中，为数值考虑引入的误差。
• 舍入误差。计算机硬件限制导致的有效数字截断引起的误差。

数值误差比较容易理解，这次就不展开去说了，后面有空再说。

（完）